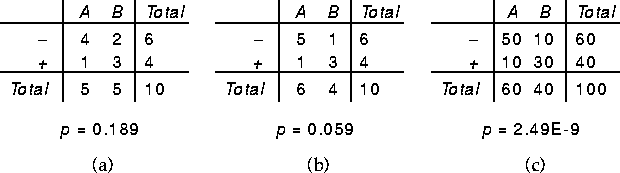Unique Challenges of
Managing Inductive Knowledge
David Jensen
Experimental Knowledge Systems Lab
Computer Science Department
University of Massachusetts
Amherst, MA 01003-4610
jensen@cs.umass.edu
Abstract:
Tools for inducing knowledge from databases, often grouped under
the term knowledge discovery, are becoming increasingly important
to organizations in business, government, and science. However, relatively
little attention has been paid to the long-term management of induced knowledge.
Induced knowledge presents unique challenges, including managing statistical
significance and inductive bias. These two challenges have important implications
for valid and efficient knowledge management.
Executive Summary
Algorithms for inducing knowledge are becoming increasingly important in
business, government, and science. In the past three years, a large number
of commercial systems for knowledge discovery have been developed and fielded,
and these systems are being actively applied by hundreds of organizations.
This increasing interest has also been reflected in the research community,
where knowledge discovery and data mining are the subject of several new
conferences, journals, and books.
Typically, these systems are concerned with producing knowledge.
They analyze a data sample to produce a set of inductive inferences that
are then applied directly by human users or encoded into other software.
However, knowledge-based systems are increasingly coming into long-term
use within organizations. This implies the need to explicitly maintain and
manage all knowledge, including knowledge that is derived inductively.
This paper argues that induced knowledge has at least two unique characteristics,
and that these characteristics impose special requirements on knowledge
management systems. The first characteristic concerns statistical significance,
characterized by a non-zero probability that any observed relationship may
be due to random variation alone. The need to evaluate statistical significance
implies that knowledge management systems must be at least loosely coupled
with systems for two other functions: data management and induction. Knowledge
cannot simply be induced and then permanently transferred to a knowledge
management system. Instead, continued communication between these systems
is necessary to effectively manage induced knowledge. The second unique
characteristic of induced knowledge is inductive bias, the ordering
of possible models imposed by a search procedure. Inductive bias provides
additional reasons that knowledge management systems should be coupled with
systems for induction.
If knowledge management systems contain inductively derived knowledge, but
fail to account for these unique challenges, they will fall prey to several
pathologies. These include faulty estimates of validity, missed opportunities
to discover useful relationships, and redundant search efforts.
The remaining three sections support these claims. The first two sections
introduce statistical significance and inductive bias, provide examples,
and present implications. Readers who already understand these concepts
may wish to skip the front portions of these sections, but they are provided
for completeness. The third section discusses briefly system design issues
in the context of these characteristics.
Statistical Significance
A particular type of uncertainty is associated with all induced knowledge.
There is a probability p that any observed relationship is merely
due to random variation. Even if there is perfect correlation between two
variables, there is still a non-zero probability that the relationship occurred
by chance alone.
An Example
For example, consider the simple data sample shown in Figure 1.
The model M, here represented as a rule, expresses a relationship between
two variables, and the data sample D provides a way of empirically evaluating
the accuracy of that model. The relationship expressed by M in the data
sample D can be compactly expressed by the contingency table in Figure 1.
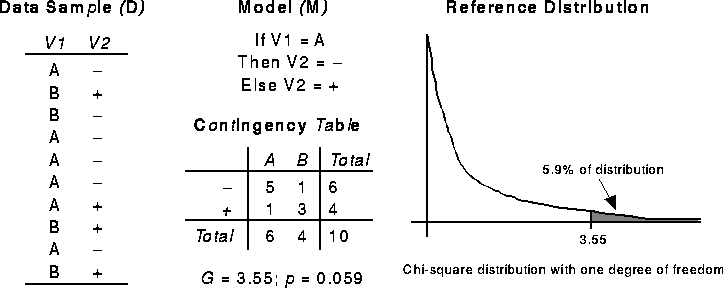
Figure 1: Example Significance Test
Assuming that M was derived independently of D, it is possible to estimate
the probability p using two things: 1) a statistic, and 2) its reference
distribution. A statistic summarizes the quality of a relationship in a
single scalar measure. A standard statistic for the type of table in Figure
1 is the G statistic.
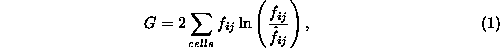
where  is the
number of occurrences, or frequency, in the cell i,j and
is the
number of occurrences, or frequency, in the cell i,j and 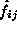 is the expected value of that cell. In this case, the expected value
is
is the expected value of that cell. In this case, the expected value
is 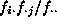 , where
, where 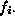 is the total frequency in
row i,
is the total frequency in
row i, 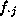 is the total
frequency in column j, and
is the total
frequency in column j, and 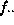 is the total of all cells in the table. The table in Figure 1
results in a G value of 3.55.
is the total of all cells in the table. The table in Figure 1
results in a G value of 3.55.
A reference distribution indicates the frequency of a statistic's values
that would be expected under the null hypothesis -- in this case,
the hypothesis that the variables V1 and V2 are independent. The reference
distribution for G is a chi-square distribution with (r-1)(c-1) degrees
of freedom, where r is the number of rows and c is the number of columns
in the table. The table in Figure 1
has one degree of freedom.
As shown schematically in Figure 1,
5.9% of the reference distribution for G is equal or greater to 3.55, indicating
that 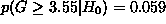 , where
, where 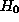 is the null hypothesis. The
probability p can be very small, but it is always non-zero.
is the null hypothesis. The
probability p can be very small, but it is always non-zero.
The Meaning of Statistical
Significance
In general, statisticians refer either to p directly or to statistical
significance. A relationship is statistically significant if its value
of p is less than some preset threshold 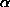 , typically 5% or 10%. An alternative approach with exactly the same
effect is to determine whether a G value exceeds a certain critical value
-- the value of G corresponding to
, typically 5% or 10%. An alternative approach with exactly the same
effect is to determine whether a G value exceeds a certain critical value
-- the value of G corresponding to 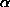 . The 10% critical value for G is 2.706 -- the value above which 10%
of G's distribution lies. The model in Figure 1
is significant at the 10% level because its G value exceeds the 10% critical
value.
. The 10% critical value for G is 2.706 -- the value above which 10%
of G's distribution lies. The model in Figure 1
is significant at the 10% level because its G value exceeds the 10% critical
value.
The probability p is distinct from what could be called the inferential
uncertainty of a relationship, the uncertainty associated with making
a particular inference. The model M might be said to have an inferential
uncertainty of 20%; based on D there appears to be a 20% probability of
making an incorrect inference when using the rule. Statistical significance
and inferential uncertainty are related, but the relationship is mediated
by several other factors discussed below.
Statistical significance is also distinct from the probability that a particular
model is ``correct.'' It is a mistake to think that, merely because a model
is statistically significant, that it is necessarily correct. Indeed, the
actual relationship could have a different functional form than the induced
model, less (or more) inferential uncertainty, different parameter values,
additional (or fewer) variables, latent variables, and many other differences.
Instead of a guarantee, statistical significance is only a minimum indicator
of validity. If an observed relationship can be explained entirely as chance
variation (e.g., p is very large), then there is little need to investigate
further. If p is very small, then additional questions about the form and
content of the relationship are worth investigating.
The discussion above suggests a design requirement for knowledge management
systems: an estimate of p should be calculated and stored along with knowledge
that has been derived inductively. This estimate can be used, along with
other information, to judge the validity of an induced model. Different
uses may imply different desired levels of statistical significance. For
example, medical treatments that are expensive or dangerous might be required
to meet higher standards of statistical significance than treatments that
are cheap and relatively benign.
Why Statistical Significance
Can Be Difficult to Determine
Based on the example above, calculating p seems relatively straightforward.
Unfortunately, the example is misleading in at least two important respects
-- M was evaluated on only a single sample of data and M was
assumed to arise independently of that sample. In reality, knowledge management
systems will have to relate rules such as M to more complex and evolving
samples of data and such rules will be derived based on extensive search
of those same samples.
These factors raise serious issues for knowledge management. The complexities
arise because p, for a given model M, depends on both the
data and the method used to find the model.
The dependence on data is reasonably obvious. The probability p depends
on the strength of the relationship identified in the data and on the size
of the sample available to test the relationship. For example, consider
the three contingency tables in Figure 2.
In each case, the associated p value was determined by comparing
the value of the G statistic to its reference distribution. Both
tables a and b have the same total frequency, but table b expresses a stronger
relationship and has a correspondingly lower value of p. Similarly, tables
b and c have a relationship of the same strength (in terms of inferential
uncertainty), but table c has a vastly lower p value because it corresponds
to a sample of larger total size.
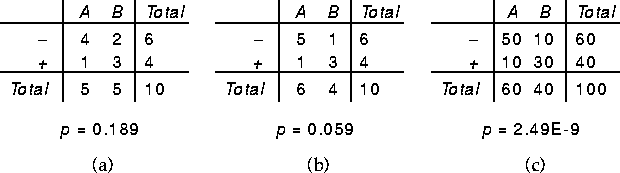
Figure 2: Three Contingency Tables
In addition to depending on the data, p depends on the number of models
examined by an induction algorithm. Consider an induction algorithm that
examines n models -- 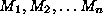 . Under the null hypothesis, each model's G statistic has a 10% probability
of exceeding 2.706, the 10% critical value for G. However, the probability
that one of the models' G statistic exceeds 2.706 is almost certainly
larger. If the predictions of each of the models are independent, then:
. Under the null hypothesis, each model's G statistic has a 10% probability
of exceeding 2.706, the 10% critical value for G. However, the probability
that one of the models' G statistic exceeds 2.706 is almost certainly
larger. If the predictions of each of the models are independent, then:
where 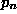 is the
probability that at least one of the n models' G values exceeds 2.706
and
is the
probability that at least one of the n models' G values exceeds 2.706
and 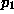 is the probability
that a single model's G value exceeds 2.706. For example, if
is the probability
that a single model's G value exceeds 2.706. For example, if 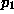 is 0.10 and 20 models are examined, then
is 0.10 and 20 models are examined, then  . In practice, induction algorithms compare thousands or tens of thousands
of different models by varying the functional form, variables used, or settings
of parameters. As a result, adjusting for these multiple comparisons becomes
essential to accurately estimate p.
. In practice, induction algorithms compare thousands or tens of thousands
of different models by varying the functional form, variables used, or settings
of parameters. As a result, adjusting for these multiple comparisons becomes
essential to accurately estimate p.
Equation 2 is one of a class of Bonferroni
equations, commonly used to adjust statistical tests for multiple comparisons
and more recently applied to induction algorithms. The adjustment is necessary
because the reference distribution for G is constructed under the assumption
of a single comparison of a model to a data sample. Making multiple comparisons
renders this reference distribution inaccurate.
A Bonferroni equation assumes that the comparisons are independent
-- i.e., that the results of one comparison tell us nothing about the outcome
of another comparison. Unfortunately, multiple comparisons by induction
algorithms are rarely independent. Multiple models generated during search
often have similar structure and use similar variables. As a result, the
comparisons are not independent, potentially rendering the Bonferroni equation
inaccurate. To a first approximation, however, potential correlation can
sometimes be ignored, and we will not deal further with this issue here.
In addition to a Bonferroni equation, there are several other techniques
that can be used to compensate for multiple comparisons even when those
comparisons are non-independent. These include randomization tests, a method
of empirically constructing reference distributions based on analyzing random
data, and cross-validation, a method of systematically providing fresh data
for evaluating the results of extensive search.
Potential Pitfalls and How
to Avoid Them
All of these techniques, however, require information about which data were
used to construct the model and what alternative models were tested during
the construction. To make this more concrete, consider the following situations:
- Unintentional data reuse: A model M is derived based on a sample
of data D. It is stored without any references to data. Later, M is tested
on data to verify its accuracy. Without records of how M was derived, it
would appear that M has been independently verified. Unfortunately, M was
``verified'' on D, the same sample used to derive it. Potential mistakes
of this kind can only be avoided if a link is maintained to the original
data used to derive a model.
- Uncoordinated, distributed search: Twenty analysts work independently
on data sample D, each evaluating the accuracy of a different model. One
analyst's model is statistically significant at the 10% level. Without the
information that other analysts are conducting similar analyses, it would
appear that a significant relationship has been identified. Considering
the actions of all the analysts (e.g., by using equation 2),
the result is not statistically significant. This indicates the importance
of maintaining records of the uses of different data samples.
- Ignoring sample size: Two models
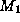 and
and 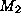 are induced
and stored with estimates of their inferential uncertainty -- the percentage
of incorrect predictions. Later, they are compared and found to be equally
useful. Unfortunately, model
are induced
and stored with estimates of their inferential uncertainty -- the percentage
of incorrect predictions. Later, they are compared and found to be equally
useful. Unfortunately, model 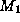 's estimate was based on data sample
's estimate was based on data sample 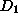 with 1000 instances; model
with 1000 instances; model 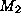 's estimate was based on data sample
's estimate was based on data sample 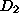 with only 10 instances. While the two models have identical inferential
uncertainty, the first estimate is far more reliable. Judgments of this
kind can only be made if a knowledge management system retains some information
about statistical significance or the data sample used to derive a model.
with only 10 instances. While the two models have identical inferential
uncertainty, the first estimate is far more reliable. Judgments of this
kind can only be made if a knowledge management system retains some information
about statistical significance or the data sample used to derive a model.
- Incremental induction: A model is developed on a small data
sample and, while suggestive of an interesting relationship, it does not
exceed a prespecified critical value. Another small sample of data becomes
available later, but it is also too small to confer statistical significance
to the model. However, the relationship would be significant if considered
in the context of both data samples together. This indicates the importance
of maintaining both tentative models and links to the original data.
These examples indicate a few of the situations where statistical significance
is both an important characteristic of induced knowledge to consider, and
why it holds implications for the design of knowledge management systems.
A second issue, inductive bias, also has important implications for
the knowledge management.
Inductive Bias
All induction algorithms search an explicit or implicit space of possible
models. Because this space must be finite, the algorithms necessarily exclude
some possible models from their search space. In addition, induction algorithms
impose an ordering on the models within their search space. They select
some models over others, based on apparent accuracy, relative complexity,
and other factors.
Machine learning researchers label these factors inductive bias.
Inductive bias is a necessary characteristic of any induction algorithm.
Indeed, induction algorithms are largely defined by their inductive bias
-- the space they search and their relative preferences within that space
are some of the most critical factors that define a particular algorithm.
Types of Bias
There are at least two types of inductive bias. Representational bias
refers to limits imposed on the search space by the selected representation.
For example, only certain types of relationships can be represented as kDNF
rules. Procedural or algorithmic bias refers to ordering or
limits imposed by search algorithm. Algorithms typically explore a space
of models sequentially, and often prefer models found earlier to equally
accurate models found later. In addition, models found early in a search
may affect what models are subsequently generated and evaluated.
One of the simplest factors that inductive bias can express is the intensity
of search. If we know that an algorithm has examined only a few potential
models, we may wish to devote additional resources to searching a larger
space. In contrast, if an algorithm examines a large search space, and can
make guarantees about finding accurate models within that space, then we
can eliminate that space from future analyses that use the same data, and
concentrate on other potential search spaces.
Particular inductive biases can be appropriate or inappropriate for particular
domains. Most obviously, if some important relationships cannot be represented
within the language an algorithm uses to express models, then no amount
of searching will find those relationships. In addition, some forms of procedural
bias are effective within some domains, but not in others.
Potential Pitfalls and How
to Avoid Them
For the purposes of managing inductive knowledge, inductive bias can affect
both validity and efficiency. Validity is partially determined by how appropriately
a search space was defined and how thoroughly it has been searched. Inductive
bias can tell us about both. Efficiency depends partially on preventing
unnecessary duplication of effort. Understanding an algorithm's inductive
bias helps compactly record what models it has examined. To make these effects
more concrete, consider the following examples:
- Misspecified Search: Other sources of knowledge in a particular
domain (e.g., domain experts) indicate that useful knowledge will be of
a specified form. An analyst might apply a particular algorithm with the
expectation that it examines models of a particular form, when it actually
does not. Information about the algorithm's bias would help determine what
space of models it will search.
- Redundant Search: A data sample is analyzed with induction
algorithm
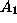 . Later,
an attempt is made to extend the previous analysis by searching with algorithm
. Later,
an attempt is made to extend the previous analysis by searching with algorithm
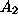 . Unfortunately, the
two algorithms have almost precisely the same inductive bias, making the
second search redundant. Clear specifications of each algorithm's inductive
bias could be used to prevent such redundancy.
. Unfortunately, the
two algorithms have almost precisely the same inductive bias, making the
second search redundant. Clear specifications of each algorithm's inductive
bias could be used to prevent such redundancy.
- Oversearching: Recent results comparing induction algorithms
employing heuristic search techniques with algorithms employing exhaustive
search have shown that, paradoxically, algorithms using heuristic search
produce models that are more accurate on new data. This phenomenon can be
explained as an effect of multiple comparisons. Being able to account for
the effects of multiple comparisons relies on being able to accurately characterize
the search spaces of different algorithms.
These examples indicate why induced knowledge is more useful when linked
to the inductive biases of available algorithms.
Implications
Understanding statistical significance and inductive bias implies that knowledge
management systems need to keep track of more than merely the final products
of induction algorithms. Specifically, knowledge management systems should
track:
- The size and identity of data samples used to induce particular
models. That is, data management and knowledge management need to be linked.
- The number and types of models examined by induction algorithms.
That is, induction algorithms and knowledge management need to be linked.
Certainly are special cases where these issues are of little concern. For
example, if nearly unlimited data are available (e.g., the domain includes
a simulation of low computational cost that can generate data on demand),
then there is little reason to retain data after it has been used once,
and models can always be verified based on new data. Similarly, if induced
models are used once and then discarded (e.g., in domains where relationships
change hourly or daily), then there is little need for long-term management
of induced knowledge.
In many situations, however, long-term management of induced knowledge is
desirable. We wish to build on previously induced relationships and make
use of data and computational resources in the most efficient way possible.
How can knowledge management systems provide the information needed to do
this, without requiring knowledge management to be deeply integrated with
other systems?
One way is to divide functions into components for knowledge management,
data management, induction, and performance:
- The knowledge management component stores, organizes, and facilitates
maintenance of represented knowledge. Each model contains a record, interpretable
by the data management component, of the data sample used to induce it and
a record, interpretable by the induction component, of the bias used to
induce it.
- The data management component stores data used by the induction
component, and provides records of the samples used to induce particular
models.
- The induction component creates new models and provides records
of the inductive bias used to induce them.
- The performance component makes inferences based on models
in the knowledge management component.
Records of data samples are relatively simple to create. Each instance (e.g.,
a patient record in a medical database) can be assigned a unique integer,
allowing a data sample to be characterized by a single vector of integers
or a bitvector that partitions a unique sorting of a database into two groups.
In other cases, where only some of the available variables are provided
in a sample, a record of a sample might need to contain both a vector recording
which instances were used and a vector recording which variables were used.
Finally, if a pseudo-random sample of instances needs to be indicated, then
recording the random seed and the total number of records in the sample
would suffice to recreate the sample on demand.
Records of inductive bias are somewhat more problematic. Part of the inductive
bias concerns representation language -- a constant for any individual induction
algorithm. However, a compact record of the path of a heuristic search is
not so simple to achieve. At a minimum, induction algorithms could record
the raw number of models examined during search and rough limits of the
search (e.g., the depth of a decision tree or the number of separate rules
in an induced ruleset). Some interactive approaches to induction (e.g.,
visualization) have an inductive bias that is almost impossible to characterize.
Even in these cases, however, records could be kept about the number and
types of relationships explored.
Clearly, this discussion only sketches how a knowledge management system
might be designed to accommodate inductive knowledge. However, it identifies
some key characteristics of such a system -- links to both the induction
and data management systems. Given the implications of statistical significance
and inductive bias, these characteristics would seem essential to a system
that effectively manages inductive knowledge.
Acknowledgements
This research is supported by DARPA/Rome Laboratory under contract No. F30602-93-C-0076.
The U.S. Government is authorized to reproduce and distribute reprints for
governmental purposes notwithstanding any copyright notation hereon. The
views and conclusions contained herein are those of the authors and should
not be interpreted as necessarily representing the official policies or
endorsements either expressed or implied, of the Defense Advanced Research
Projects Agency, Rome Laboratory or the U.S. Government.
About this document ...
This document was generated using the LaTeX2HTML
translator Version 96.1 (Feb 5, 1996) Copyright © 1993, 1994, 1995,
1996, Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
© David Jensen