Juergen Angele, Stefan Decker, Rainer Perkuhn, and Rudi Studer
Institute AIFB
University of Karlsruhe (TH)
D-76128 Karlsruhe, Germany
e-mail: { angele | decker | perkuhn | studer }@aifb.uni-karlsruhe.de

Abstract

1 INTRODUCTION

• KARL is a conceptual specification language. KARL provides modeling primitives on a high level of abstraction independent of realization aspects. KARL distinguishes several types of knowledge and defines different language primitives for them.
• KARL is a formal specification language. Thus the language primitives get a defined meaning which allows a precise and unequivocal description. The semantics of KARL has been defined based on the semantics of predicate logic and dynamic logic which have been combined to define a declarative semantics for the entire language.
• KARL is an operational knowledge specification language. Based on a constructive semantics which corresponds to the declarative semantics an interpreter has been implemented which allows to build the model of expertise using a prototyping approach.

It is now two years ago that the current version of KARL has been defined. In the meantime several models of expertise have been specified in KARL. Using KARL it has been started to build up a library of formally specified problem-solving methods: Hill Climbing, Chronological Backtracking, Beam Search, Cover-and-Differentiate, Board-Game Method, Propose-and-Exchange, and Propose-and-Revise.

In this paper we describe a conceptual structure of PSMs. It distinguishes the functional specification consisting of input-output roles and pre- and postconditions, and the operational specification. We describe how the language KARL has been modified and extended to New KARL which relies on this conceptual structure. One of the main goals of this extension was to preserve the properties of KARL to be (i) a conceptual, (ii) a formal, and (iii) an executable language. In future the properties of such formally represented PSMs may be exploited for the retrieval of PSMs out of a library and for supporting the configuration and adaptation process of PSMs. Additionally, such formally represented PSMs are open for further analysis, like verification of correctness or analysis of their efficiency under different conditions.

The paper is structured as follows. Section 2 describes the conceptual structure of a PSM and the needs which have to be met for configuring components of PSMs. In section 3 new language primitives are introduced for KARL which allow to represent a PSM of this conceptual structure. Related work is discussed in section 4. Finally we give a conclusion.

2 THE CONCEPTUAL MODEL OF A PSM

This section presents the notion of a PSM in the context of the method-to-task paradigm that emerged from Components of Expertise [Steels, 1990], Task Structure Analysis [Chandrasekaran, Johnson, and Smith, 1992], PROTÉGÉ-II [Puerta et al., 1992], and CommonKADS [Schreiber et al., 1994a]. We do not want to go into details about the distinction of generic (problem solving) and domain specific (ontology) knowledge. We do neither mention explicitly the mappings between these two different kinds of knowledge since these can be treated as a special case of any mapping of a PSM to its environment.

2.1 Representing PSMs

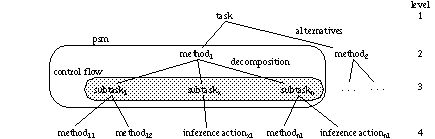
Figure 1: Embedding the notion of PSM into the method-to-task paradigm

A PSM decomposes a task into new subtasks. According to the divide-and-conquer principle this is done repeatedly downto a level of subtasks for which the solution is obvious and can be written down in a straightforward manner as an elementary inference action. In addition to the decomposition the PSM has to specify the control flow of the subtasks, i.e. the ordering in which the subtasks can be accomplished. Or, to put it the other way around, as long as one is interested in specifying the control flow one has to decompose the task further.

Although the decomposition eases the effort to find (partial) solutions it introduces the new problem of building the solution of the overall task from the partial solutions, especially the problem of integrating the concepts which are specified in different subtask ontologies into one global data flow (cf. section 2.2).

As an alternative to specify the same or a similar method (decomposition and control flow) or an elementary inference action for several times a promising approach is reuse. While the odd levels in the hierarchy (figure 1) are responsible for setting up the goals, the even levels offer solutions of how to reach the goals. Every node on an even level is a possible candidate for reuse, but one has to find the right level of granularity for reasonable reuse. The lower levels promise a high probability that an adequate matching reusable component exists but the gain is very small. The greatest benefit would be achieved if one can reuse a big component, i.e. a node on a very high level, but the probability of finding a matching one is very small. So, to meet the adequate tradeoff of reducing the effort of adapting on the one hand, and of repeating work that has already been done on the other hand, one has to consider all nodes in between as possible candidates for reuse.

A KARL specification of a PSM corresponds to one instance of the task-method-hierarchy, i.e. during configuration one of the alternatives has been selected. In principle, a KARL specification contains all the fragments which correlate to the nodes in the hierarchy and are possible candidates for reuse. These fragments are to be specified in a way that they really can be handled as components.

In order to support reuse one has to provide means to describe the functionality of the components from a competence point of view, i.e. a description of the functionality not regarding internal aspects of the component (of how this functionality is realized) (compare e.g. [Fensel, 1995b]). It would be necessary to describe the interface to the environment (the input/output), the conditions which are assumed to be held before executing the component, and the conditions which describe the changes affected by executing the component. This issue is captured by pre-/postcondition specifications as they are well-known from software engineering.

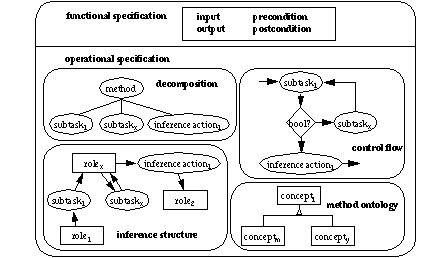
Figure 2: (Parts of the) Description of a PSM

To date, KARL focuses on capturing the description of the operational specification, but it lacks the capability to describe the functional specification of a PSM. The extension of the language KARL aims at specifying the operational part of a PSM exactly as it is shown in figure 2, that is only partially covered in the current version of KARL. New KARL provides primitives to distinguish clearly between the decomposition, the inference structure, the control flow, and the method ontology of a PSM. By this, there is no explicit representation of a single task and a single inference layer as in current KARL. But it is easy to derive this task or inference layer view from the method-to-task decomposition tree of figure 1 by extracting views solely on the odd rsp. the even levels.

Other newly introduced primitives aim at specifying the pre-/postconditions for reusable components. These conditions can then be matched against the assumptions and goals the tasks have set up and are used this way to index and to retrieve the reusable components. A further improvement would be the possibility to measure the mismatch to support the decision for the tradeoff between reuse (plus adapting) or further decomposition by hand.

We assume that the space of all PSMs is structured according to family resemblances. Every PSM has annotated a description of the functionality in form of pre- and postconditions, e.g. a precondition of the PSM Propose-and-Revise is the existence or availability of knowledge about propose rules, constraints, and fix rules (cf. [Fensel, 1995b]). This relation can be exploited in two directions: The applicability of Propose-and-Revise follows from the existence of the knowledge; or the other way around, the suggestion of Propose-and-Revise as a possible reuse candidate may trigger and guide a further elicitation process of this specific type of knowledge.

2.2 The Notion of Method and Task Ontologies

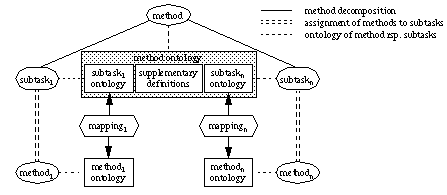
Figure 3: Ontologies within the method-to-task paradigm

Assuming that a PSM is decomposed into subtasks the problem arises of how to make the method ontology independent of the selection of more elementary methods for solving the subtasks of the PSM. In order to get rid of that problem the notion of a subtask ontology is introduced [Studer et al., 1996]. The subtask ontology defines all the concepts and relationships which are used for specifying the functional behaviour of the subtask. In essence, the method ontology is then derived from the various subtask ontologies by combining them and by introducing additional concepts and constraints. As a consequence, the subtask ontologies provide a context for mapping the (global) method ontology to the ontologies of the submethods which are used for solving the subtasks.

Of course, in general there are some differences between a subtask ontology and the ontology of the method used to accomplish the subtask. Therefore, one has to define mappings between these ontologies (compare e.g. [Gennari et al., 1994]) in order to transform the structure of the subtask ontology into the structure of the method ontology and vice versa.

It is obvious that these mappings can be specified in the same way as the mappings which are used to map the generic PSM terminology to the domain specific terminology as defined by the domain layer of the model of expertise. I.e. within our framework of tasks and methods we use the same kind of mappings for handling ontology transformations within a method as well as between the generic method ontology and the domain ontology.

3 REPRESENTING PSM`S IN NEW KARL

KARL has been evaluated the last years in a number of case studies. One of the largest one was the Sisyphus II project which has been used to compare different knowledge engineering approaches. In this project an elevator configuration task has been posed [Schreiber and Birmingham, 1996]. For configuring an elevator values have to be assigned to a predefined set of parameters. These assignments have to fulfil a number of domain-specific contraints. To accomplish this task we used a variant of the PSM Propose-and-Revise ([Poeck et al., 1996], [Angele, 1996]). Because we gained many insights during this project we use this model for our examples in the following.

3.1 Ontologies

3.1.1 Method ontology

For instance within the revise step of Propose-and-Revise two different sets of parameter-value pairs must be handled: the current set of pairs and a set of pairs to whom a fix combination has been applied. The method ontology defines the type as follows:

TYPE parameter-value-pairs
par-name: {};
par-value: {};
END;

The two stores which contain different sets of parameter-value pairs each defines its own set of parameter-value pairs by referring to the structure information within the method ontology. One store defines the set of old parameter-value pairs:

CLASS old-pairs: parameter-value-pairs.

Another store contains the set of new parameter-value pairs (after the application of the fix combination):

CLASS new-pairs: parameter-value-pairs.

This means that the classs old-pairs and new-pairs have the structure defined by the type parameter-value-pairs, i.e. the same attributes and attribute restrictions as parameter-value-pairs, but their extensions are independent from each other.

3.1.2 Mapping Ontologies

• Domain layer formulae expressed in terms of the domain ontology have to be transformed to formulae expressed in one of the method ontologies at the inference layer and vice versa.
• Formulae expressed in a subtask ontology have to be transformed to formulae expressed in the ontology of a submethod.

• It determines which facts and rules of the source part are used. It combines facts of the source part to new facts and it combines mapped facts to new facts of the destination part.
• It maps parts of the two different signatures of the two different ontologies to each other.
• It transforms formulae expressed in terms of one ontology into formulae expressed in terms of the other ontology.

The unary mapping operator map performs the second and third item. The parameter of map may contain variables for function symbols, predicate symbols, elements, values, classes, attributes, rule names and entire sub-formulae which allows to transform several formulae by one mapping expression.

For instance the PSM Propose-and-Revise uses domain specific derivation rules (propose rules) which derive the values of parameters from the values of either input parameters or parameters which have already been tackled. To apply these derivation rules correctly the PSM must know which parameter depends on which other parameters. This information is implicitly available within the derivation rules. For instance the derivation rule (2):

par(selected_platform_model, "2.5B") <- par(platform_depth, 60).

determines the value of the parameter selected_platform_model using the value of the parameter platform_depth. In KARL we had to model these dependencies separately a second time using facts of the following form:

depends_on(selected_platform_model, platform_depth).

Besides the additional huge effort this raised also consistency problems, because the same information is modeled twice.

With our new map operator in New KARL this information may be gained directly from the derivation rules:

MAPPING Map-Attributes
IN DOMAIN-LAYER;
OUT Parameters;

map(par(X,Y) <- par(U,V)) |-> (depends_on(map(X), map(U))).
/* Maps all propose rules which fit to this form to a set of dependency facts.
Our example rule is mapped to the fact depends_on(selected_platform_model,
platform_depth). If not stated otherwise map(X) = X' holds.*/
depends_on(X,Z) <- depends_on(X,Y) /\ depends_on(Y,Z).
/* this rule models transitive dependencies */
END;

So every propose-rule at the domain layer leads to a set of instances of the binary relationship depends_on describing the parameter dependencies at the inference layer.

3.2 Tasks and Methods

To describe the goal of a task, its assumptions, and to describe the functional specification of a PSM New KARL provides pre- and postconditions:

• Pre- and postconditions specify the input and the output of a method and the functional relation between input and output. Thus they describe what the method achieves and what preconditions are necessary.
• The retrieval of reusable methods may be supported by matching the goals of the current task with the postconditions and the requirements which have to be met before executing the method with the preconditions. This may in future allow to index a method semi-automatically and may support the adaptation of the method to the needs at hand.
• In future pre- and postconditions may be used to verify the operational description of methods against this functional specification and to verify whether a PSM performs the given task using the given domain knowledge.

TASK < task name >
IN inroles1,...,inrolesn.
OUT outroles1,..,outrolesm.
ONTOLOGY
< type definitions >
< role definitions > /* definition of input, output roles in top-level tasks */
< mapping definitions >
PRE < rules, constraints >
POST < rules, constraints >
METHOD < method name > /* optional, refers to a method which performs the task */
END;

A method is defined by its functional specification and by an operational specification which establishes subtasks, specifies elementary inference actions and describes the control flow between those parts. Mappings are necessary to map the ontology of the task to the method (which accomplishes the task):

METHOD < method name >
IN inroles1,...,inrolesn.
OUT outroles1,..,outrolesm.
ONTOLOGY
< type definitions >
< role definitions > /* definition of input, output roles */
< mapping definitions >
PRE < rules, constraints >
POST < rules, constraints >
DECOMPOSITION
< subtask names, names of elementary inference actions >
DATAFLOW
< role definitions > /* definition of internal roles */
< task definitions> /* definition of subtasks established by this method */
< definition of elementary inference actions >
CONTROL
< variable definitions >
< set of statements >
END;

The control part of a method describes the control flow between different subtasks and elementary inference actions. The data flow part describes the subtasks, specifies elementary inference actions, describes the roles, and defines the data flow between them. Thus the data flow together with the control flow may be seen as an operational specification of the functional specification given by the pre- and postconditions of the method. As a consequence of this structure there is no longer a common inference and control layer of a model of expertise. Instead every method describes its own part of the inference layer and of the control layer.

An example for a precondition of a method is given for the problem-solving method Propose-and-Revise: the propose-rules have to be acyclic. A propose-rule determines a value for a parameter dependent on the values of other parameters. Acyclic means that no value may depend transitively on itself.

Using the above mentioned relationship depends_on (see section 3.1.2) a precondition for the PSM Propose-and-Revise may be defined which assures that the parameter dependencies are acyclic (relationship p of role r is named r.p):

METHOD Propose-and-Revise
IN Parameters;
...
PRE
! Parameters.depends_on(A1, A2) -> ¬ Parameters.depends_on(A2, A1).
/* If A1 depends on A2 then A2 must not depend on A1
(the ! sign indicates a constraint) */
POST
...
END;

3.3 Technical Details

3.3.1 Surmounting Horn logic

Sometimes it is argued that a specification language, as KARL is claimed to be, must not be executable because this restricts its expressibility too much [Hayes and Jones, 1989]. In contrast to that we think that at the moment a promising way to validate such a specification is to test it. So a formal model which can not be tested is difficult to validate if the model has grown to a practical size because then the complexity is so large that the specification can not be validated purely by reading it. Additionally mechanization procedures such as theorem provers are much too slow to be of practical value. So from our point of view the solution to this problem can not consist of dropping the restriction to Horn logic.

To drop partially the restriction to Horn logic (at least syntactically) New KARL-rules are extended to the following form:

H <- B

where H is a conjunction of atoms (3) and B is an (not necessarily closed) arbitrary formulae. Variables in H and free variables in B are universally quantified at the front of the rule.

In [Lloyd and Topor, 1984] a simple Horn axiomatization is described for this extension and thus it can be easily integrated into the constructive semantics of KARL and based on that into the interpreter of KARL.

Let us give an example. In our class hierarchy we want to find the leaves of this hierarchy. In the current version of KARL this must be expressed using the following rules:

not_leaf(Y) <- X <= Y /\ X <> Y.
leaf(X) <- X <= Y /\ ¬ not_leaf(X).

In New KARL this may be expressed by the following (extended) rule:

leaf(X) <- \-/ Y (Y <= X -> X = Y).

3.3.2 Access to the domain ontology

For instance given the following class definition:

CLASS elevator
car-capacity-range: {REAL};
speed:{REAL};
...
END;

Used in rules signature-formulae together with variables for the attributes allow the attributes and the range restrictions of the attributes of the classes and relationships to be accessed.

The following rule collects all single-valued element-attributes of the class elevator in the value of the set-valued attribute single_valued_element_attributes of object o:

o[single_valued_element_attributes:: {X}] <- elevator[X: {}]s.
/* the signature atom is subscribed by an s */

3.3.3 Rules as objects

In order to access and handle domain rules they may be addressed by unique rule names. A named domain rule is defined as follows:

r: H <- B, where r is a unique rule name and H <- B is a rule.

At the domain layer a predefined class RULE without further attributes exists containing all named rules at the domain layer as elements. The elements of this class are addressed by their rule names. Rule objects may be treated as normal objects, they may for instance be related to another object by a part-of relation.

In our model to configure elevators fix rules may be named by f(1), f(2),... and constraint rules may be named c(1), c(2),.... This allows to assign fix rules to the constraint rules they fix by facts of the following form:

fixes(f(1), c(2)).
/* fix 1 fixes a violation of constraint 2 */

Rule objects may be accessed in other rules (for instance to select some rule objects) by their rule name. For instance in order to select all rules named f(X) and to put them into a subclass Fixes of class RULE the following rule may be given:

f(X) # Fixes <- f(X) # RULE.

This allows to select all fix rules at the domain layer in order to map them to corresponding rules at the inference layer in our model.

3.3.4 Rules and States

newvalue(Parname,V + 2) <- par(Parname, V).

and a second inference action assigns the new values to the parameters:

par(Parname, V) <- newvalue(Parname, V).

For the same reasons it is not possible to specify the input/output behavior of an inference action which deletes facts from a store. To remedy this while preserving the declarative semantics we introduce techniques developed in linear temporal logic programming (see [Orgun and Ma, 1994] for an overview) for New KARL.

We model the transition from one state to another state with the operators first and next (O). The operator first describes what is valid in the initial state and next describes the following states. For our purposes it is sufficient to allow only two kinds of clauses: computation clauses und output clauses. In a computation clause all literals are (implicitly) annotated with the first operator. The head of an output clause is annotated with a next operator, meaning that if the head can be derived it is included in the output stores. The input from the input stores is implicitly annotated with a first.

There is a simple direct transformation of linear temporal logic programs to normal logic programs: an extra argument is added to every predicate symbol. This extra argument is used as a counter of the valid state. A 0 (zero) at this extra argument position is used instead of the first operator. The next operator is translated to incrementing the actual state counter. Using this transformation the semantics of an inference action is the perfect Herbrand model of the contents of the inference action and the input stores. Change may thus be modeled in a natural way:

O par(Parname,V + 2) <- par(Parname, V).

3.3.5 Evaluation of rule objects

EVAL(s,c).

For instance the PSM Propose-and-Revise stores a set of fix-rules in the store fix-combination which should be applied in the inference action apply-fix-combination to repair a violation of a constraint:

STORE fix-combination
CLASS fix-rules: RULE';
END;

INFERENCE ACTION apply-fix-combination
IN fix-combination, old-pairs;
OUT new-pairs;

EVAL(fix-combination, fix-rules);
/* this evaluates the rules stored in class fix-rules in store fix-combination */
END;

By this way it is possible to collect all fix rules at the domain layer, to map them to corresponding rules at the inference layer, to select an appropriate subset of them at the inference layer if a constraint violation occurs and to apply them at the inference layer to repair the constraint violation.

3.3.6 Further improvements

3.4 Semantics of New KARL

The mapping operator in New KARL performs an extended matching. Be map(F1) |-> F2 the definition of a mapping operation, where F1 and F2 are formulae containing mapping variables for functions, predicates, objects, attributes, and formulae. A substitution s of the mapping variables in F1 with corresponding symbols and formulae to the formula s (F1) which matches a given fact or rule determines the output s (F2) of the mapping operator.

In KARL the semantics of an inference action is defined as the perfect Herbrand model of its input facts and the rules of the inference action. The content of an output store is given by that subset of the perfect Herbrand model which fits to the signature (class definitions and relationship definitions) of the output store. In New KARL the semantics of an inference action is the perfect Herbrand model of the same set of rules and facts plus the set of dynamic rules (rule objects). The content of an output store is given by the subset of those facts which are annotated by the next operator and which fit to the signature of the output store.

For the other extensions the semantics of KARL must be modified only slightly. Signature-atoms are facts which describe the structure of classes and relationships. They contribute as normal facts to the perfect Herbrand model of the domain layer. As already mentioned for the generalized rules a simple axiomatization in current KARL exists. Similarly the lists and the additional possibilities to handle sets may be axiomatized in current KARL. The pre- and postconditions and the generalized expressions in tests of loops and alternatives have the form of constraints in current KARL for which also a semantics has been already defined.

So the basic ideas of the semantics of KARL may be conserved and the current semantics had to be modified at those points mentioned above. An alternative for defining the semantics of New KARL is the general framework set up by MLPM (Modal Logic of Predicate Modification) [Fensel and Groenboom, 1996]. MLPM allows the characterization of the dynamic reasoning process in New KARL. Within this framework, not only an efficient execution of the specification is possible, but also reasoning about the specification itself.

4 RELATED WORK

CML is a semi-formal language and offers a set of primitives to describe the CommonKADS model of expertise [Schreiber et al., 1994b]. On an abstract level the structure of a CML and a New KARL specification are very similar. But CML has no formally defined semantics and according to the CML grammar every part of the specification besides the names, the roles, and the decomposition is rewritten as free text. In contrast to this, New KARL pursues the idea that the complete model has a formally defined semantics, especially the parts that are only natural language descriptions in CML, e.g. the control flow and the competence. The same holds already for (old) KARL but in addition New KARL considers also the notion of PSMs and tasks as well as method and (sub-)task ontologies. [Schreiber et al., 1994b] sketches already the necessity of ontology mappings and offers a preliminary version - with the disclaimer that this has to be refined in the near future.

The newly introduced language primitives relate to corresponding primitives in ML2 in the following way. The integration of the concept of PSMs into the language New KARL allows to describe all aspects of PSMs formally. This allows to describe PSMs precisely and unambiguously and opens them for discussion and for further analysis. Up to now no corresponding primitives are available in ML2. Domain layer and inference layer are related in ML2 via a classical object-meta relationship. In contrast to that in New KARL two different languages for each layer using different signatures are related by the mappings which transform expressions of one language into expressions of the other language. Together with the handling of rules as objects this allows to evaluate rules in an environment which may be dynamically configured during the problem-solving process. In ML2 domain formulae are mapped to variable-free terms at the inference layer. Their truth may be evaluated within the domain layer using reflection rules. So the environment in which such formulae are evaluated is fixed in advance. In New KARL all elements of the domain ontology are now accessible in formulae. This supports the reuse of both the domain layer for another task and the PSM within another domain. In ML2 there is no possibility to access the sorts and the orderings of the order sorted logic at the domain layer. The extended rules in L-KARL reduce the gap between Horn logic and full first-order logic and allow to express things more adequately. Still all parts of L-KARL may be axiomatized in Horn logic which allows to execute the model with reasonable efficiency. The price which had to be paid for this possibility is a compromise between executability and expressiveness: L-KARL is restricted to Horn logic in order to provide efficient executability whereas ML2 uses full first-order logic. On the other hand in ML2 only the Horn logic subset can be validated by the simulator. A detailed comparison between ML2 and (old) KARL may be found in [Fensel and van Harmelen, 1994].

The conceptual method-to-task framework as introduced for New KARL is also similar to the notion of task and methods in PROTÉGÉ-II ([Eriksson et al., 1995], [Gennari et al., 1994]). Especially the notion of a method ontology is taken from the PROTÉGÉ-II approach. Within PROTÉGÉ-II an ontology of mapping relations is defined for connecting methods and domains [Gennari et al., 1994]. Gennari et al. define for instance renaming mappings, filtering mappings, and class mappings. All these types of mappings may be described by the mapping operator map of New KARL. Thus New KARL provides means for formalizing the types of mappings which are used to relate a method ontology to an application ontology within the PROTÉGÉ-II framework.

The TASK approach [Pierret-Goldbreich, 1994] claims to be different from KADS approaches in dealing with flexible problem-solving and dynamic behaviour specification. TASK proposes three different languages for the conceptual, the formal and the implementation level respectively [Talon and Pierret-Goldbreich, 1996] - and by this suffers from the same disadvantages as described above. The strongest affinity between TASK and MIKE is on the formal level, i.e. between New KARL and the formal language TFL that is based upon abstract data types (ADT) [Pierret-Goldbreich and Talon, 1995]. ADTs are well-suited to specify the functional description of a PSM but they are insufficient to specify the operational part. This aspect, to treat the different parts of a PSM specification as one unit, is emphasized in New KARL. TASK ignores the specification of the operational part of a PSM - especially the control flow - because it considers methods as pre-built components that are configured during runtime via oppurtunistic reasoning. Similar to our approach TASK postulates the necessity to specify goals. This is also done in the framework of ADTs [Pierret-Goldbreich, 1996] but since goals are treated as separate entities that are linked neither to processes nor tasks it remains unclear how they can be exploited for reuse rsp. oppurtunistic configuration.

DESIRE ([Treur, 1994], [van Langevelden, Philipsen, and Treur, 1993], [van Langevelden, Philipsen, and Treur, 1992]) is a formal KBS specification language that also does not rely on the KADS model of expertise. DESIRE uses linear temporal logic with partial models to define the semantics of a reasoning process, whereas New KARL uses temporal logic to specify the input/output behaviour of an inference action. It is therefore not only directly possible to define the notion of a state change in New KARL, e.g. what should be true in the next reasoning step, but it is also possible to describe the semantics of the whole inference process in terms of a temporal Herbrand model. In DESIRE the specification of the input/output of a reasoning module is done by defining an input/output signature. New KARL has a more general approach: signatures are translated, but also entire formulae.

5 CONCLUSION

• The integration of the concepts task and PSM into the language itself allows to formally represent all conceptual aspects of tasks and PSMs and their relationships. The assumptions and goals of tasks are represented via pre- and postconditions. A PSM is represented by its functional specification using pre- and postconditions and by its operational specification. Thus PSMs may be represented unambiguously and are open for further analysis. Additionally this knowledge may in future be exploited (i) for verifying whether an operational specification of a PSM fulfils its functional specification, (ii) for verifying whether a PSM together with the available domain knowledge performs the given task, (iii) for supporting the retrieval of the PSM out of a library of PSMs, and (iv) for adapting the PSM to the needs at hand.
• The access to the entire ontology and to the ingredients of the rules at the domain layer by the introduced mapping operator allows to exploit all information of the domain layer by the PSM at the inference layer. This supports the reuse of the PSM in another domain and the reuse of the domain layer for another task.
• The introduced mappings allow to map expressions described in one terminology into expressions described in another terminology. This supports the configuration of PSMs which come with their own method ontology when they have been retrieved from a library of PSMs.
• Handling domain rules as objects and selectively evaluating them at the inference layer allows to dynamically configure the environment in which a rule is evaluated at the inference layer. PSMs like Propose-and-Revise which selectively evaluate rules within the environment of newly computed data may thus be represented more adequately.

After having defined a new version of KARL, namely New KARL, current work is in progress to (i) define a complete formal semantics for New KARL which also allows to reason over the specification itself and to (ii) implement an interpreter for New KARL.

Acknowledgement

Footnotes

(2) In the following examples we use the syntax of predicate logic instead of KARL's syntax to improve readability for those people not entirely familiar with KARL.

(3) The syntax of atoms in L-KARL differs from the syntax of atoms in predicate logic, because L-KARL is based on F-logic [Kifer, Lausen, and Wu, 1995].

(4) At the domain layer there is no separation of structure information (types) and the extension.

References

J. Angele, D. Fensel und R. Studer: Domain and Task Modeling in MIKE. In: A. Sutcliffe, D. Benyon, F. van Assche (Eds.): Domain Knowledge for Interactive System Design, Proceedings of IFIP WG 8.1/13.2 Joint Working Conference, Geneva, May 1996, Chapman & Hall, 1996.

J.A. Breuker and W. van de Velde (Eds.): The CommonKADS Library for Expertise Modeling. IOS Press, Amsterdam, 1994.

B. Chandrasekaran, T.R. Johnson, and J.W. Smith: Task-Structure Analysis for Knowledge Modeling. In: Communications of the ACM, 35(9), 1992, 124-137.

S. Decker, M. Erdmann, and R. Studer: A Unifying View on Business Process Modelling and Knowledge Engineering. In: Proceedings of the 10th Banff Knowledge Acquisition for Knowledge Based Systems Workshop (KAW`96), Banff, Canada, November 9-14, 1996.

H. Eriksson, Y. Shahar, S.W. Tu, A.R. Puerta, and M.A. Musen: Task Modeling with Reusable Problem-Solving Methods. In: Artificial Intelligence, 79, 2, 293-326.

D. Fensel: The Knowledge Acquisition and Representation Language KARL. Kluwer Academic Publisher, Boston, 1995.

D. Fensel: Assumptions and Limitations of a Problem Solving Method: A Case Study. In: Proceedings of the 9th Banff Knowledge Acquisition for Knowledge Based Systems Workshop (KAW`95), Banff, Canada, February 26 - March 3, 1995.

D. Fensel and R. Groenboom: MLPM: Defining a Semantics and Axiomatization for Specifying the Reasoning Process of Knowledge-Based Systems. In: Proceedings of the 12th European Conference on Artificial Intelligence (ECAI`96), Budapest, August 12-16, 1996.

D. Fensel and R. Straatman: Problem Solving Methods: Making Assumptions for Efficiency Reasons. In: Shadbolt, N. et al. (Eds.): Proceedings of the 9th European Knowledge Acquisition Workshop (EKAW`96), Nottingham, United Kingdom, May 1996, Springer LNAI, vol. 1076, 1996, 17-32.

D. Fensel and F. van Harmelen: A Comparison of Languages which Operationalize and Formalize KADS Models of Expertise. In: The Knowledge Engineering Review, vol. 9, no. 2, June 1994.

D. Fensel, J. Angele, and R. Studer: The Knowledge Acquisition and Representation Language KARL. To appear in: IEEE Transactions on Knowledge and Data Engineering, 1997.

J.H. Gennari, S. Tu, Th.E. Rothenfluh, and M.A. Musen: Mapping Domains to Methods in Support of Reuse. In: International Journal of Human-Computer Studies (IJHCS), 41, 399-424.

I.J. Hayes and C.B. Jones: Specifications are Not (Necessarily) Executable. In: IEEE Software Engineering, 4 (6), November 1989, 320-338.

M. Kifer, G. Lausen, and J. Wu: Logical Foundations of Object-Oriented and Frame-Based Languages. In: Journal of the ACM, vol. 42, 1995, 741-843.

D. Landes and R. Studer: The Treatment of Non-Functional Requirements in MIKE. In: Proceedings of the 5th European Software Engineering Conference (ESEC\xab 95), Sitges, 1995, Springer LNCS, vol. 989, 1995.

J. W. Lloyd and R. W. Topor: Making Prolog More Expressive. In: Journal of Logic Programming, vol. 1, no. 3, 1984.

A. Newell: The Knowledge Level. In: Artificial Intelligence 18, 1982, 87-127.

M. A. Orgun and W. Ma: An Overview of Temporal and Modal Logic Programming. In: D. M. Gabbay and H. J. Ohlbach (Eds.): Proceedings of the First International Conference on Temporal Logic (ICTL`94), Gustav Stresemann Institut, Bonn, Germany, July 11-14, LNAI 827, Springer-Verlag Berlin Heidelberg, 1994, 445-479.

C. Pierret-Goldbreich: TASK MODEL: A Framework for the Design of Models of Expertise and their Operationalization. In: Proceedings of the 8th Banff Knowledge Acquisition for Knowledge Based Systems Workshop (KAW`94), Banff, Canada, January 30 - February 4, 1994, 37-1 - 37-22.

C. Pierret-Goldbreich: Modular and Reusable Specifications in Knowledge Engineering: Formal Specification of Goals and their Development. In: Proceedings of the 6th Workshop on Knowledge Engineering Methods and Languages (KEML`96), Gif sur Yvette, France, January 15-16, 1996.

C. Pierret-Goldbreich and X. Talon: An Algebraic Specification for the Dynamics of Flexible Systems in TASK. In: Proceedings of the 9th Banff Knowledge Acquisition for Knowledge Based Systems Workshop (KAW`95), Banff, Canada, February 26 - March 3, 1995, 31-1 - 31-22.

K. Poeck, D. Fensel, D. Landes, and J. Angele: Combining KARL and CRLM for Designing Vertical Transportation Systems. In: International Journal of Human-Computer Studies (IJHCS), 44, 1996, 435-467.

A. R. Puerta, J. W. Egar, S. W. Tu, and M. A. Musen: A Multiple-Method Knowledge Acquisition Shell for the Automatic Generation of Knowledge Acquisition Tools. In: Knowledge Acquisition, 4, 1992, 171-196.

A.Th. Schreiber and W.P. Birmingham (Eds.): International Journal of Human-Computer Studies (IJHCS), 44, Special Issue: The Sisyphus-VT Initiative, 1996.

A.Th. Schreiber, B.J. Wielinga, R. de Hoog, H. Akkermans, and W. van de Velde: CommonKADS: A Comprehensive Methodology for KBS Development. In: IEEE Expert, December 1994, 28-37.

G. Schreiber, B. Wielinga, H. Akkermans, W. van de Velde, and A. Anjewierden: CML: The CommonKADS Conceptual Modelling Language. In: Steels, L. et al. (Eds.): A Future for Knowledge Acquisition, Hoegaarden, Belgium, September 1994, Springer LNAI, vol. 867, Berlin, 1994, 1-25.

G. Schreiber, B. Wielinga, and J. Breuker (Eds.): KADS. A Principled Approach to Knowledge-Based System Development. Knowledge-Based Systems, vol. 11, Academic Press, London, 1993.

L. Steels: Components of Expertise. In: AI Magazine, 1990.

R. Studer, H. Eriksson, J.H. Gennari, S. Tu, D. Fensel, and M.A. Musen: Ontologies and the Configuration of Problem Solving Methods. In: Proceedings of the 10th Banff Knowledge Acquisition for Knowledge Based Systems Workshop (KAW`96), Banff, Canada, November 9-14, 1996.

X. Talon and C. Pierret-Goldbreich: TASK: A Framework for the Different Steps of a KBS Construction. In: Proceedings of the 6th Workshop on Knowledge Engineering Methods and Languages (KEML`96), Gif sur Yvette, France, January 15-16, 1996.

A.T. Teije, F. van Harmelen, M. Reinders: Si(ML)2: A Prototype Interpreter for a Subset of (ML)2. ESPRIT Project P5248 KADS-II, Report KADS-II/T1.2/TR/UvA/005/1.0, University of Amsterdam, 1991.

J. Treur: Temporal Semantics of Meta-Level Architectures for Dynamic Control of Reasoning. In: Fribourg et. al. (Eds.): Logic Program Synthesis and Transformation - Meta Programming in Logic. Springer Verlag, LNCS 883, 1994.

F. van Harmelen and M. Aben: Structure-Preserving Specification Languages for Knowledge-Based Systems. In: International Journal of Human-Computer Studies (IJHCS), 44, 1996, 187-212.

F. van Harmelen and J. Balder: (ML)2: A Formal Language for KADS Conceptual Models. In: Knowledge Acquisition, 4, 1, 1992.

I. A. van Langevelden, A. W. Philipsen, and J. Treur: Formal Specification of Compositional Architectures. In: Proceedings of the 10th European Conference on Artificial Intelligence (ECAI`92), Vienna, Austria, August 3-7, 1992.

I. A. van Langevelden, A. W. Philipsen, and J.Treur: A Compositional Architecture for Simple Design Formally Specified in DESIRE, In: J. Treur and Th. Wetter (Eds.): Formal Specification of Complex Reasoning Systems, Ellis Horwood, New York, 1993