Knowledge Acquisition, Validation, and Maintenance in
a Planning System for Automated Image Processing
Steve A. Chien
Jet Propulsion Laboratory, California Institute of Technology
4800 Oak Grove Drive, M/S 525-3660, Pasadena, CA 91109-8099
steve.chien@jpl.nasa.gov
Abstract:
A key obstacle hampering fielding of AI planning applications is the
considerable expense of developing, verifying, updating, and maintaining
the planning knowledge base (KB). Planning systems must be able to compare
favorably in terms of software lifecycle costs to other means of automation
such as scripts or rule-based expert systems. Consequently, in order to
field real systems, planning practitioners must be able to provide: 1.
tools to allow domain experts to create and debug their own planning knowledge
bases; 2. tools for software verification, validation, and testing; and
3. tools to facilitate updates and maintenance of the planning knowledge
base. This paper begins by describing a planning application of automated
image processing and our overall approach to knowledge acquisition for
this application. This paper then describes two types of tools for planning
knowledge base development: static KB analysis techniques to detect certain
classes of syntactic errors in a planning knowledge base; and completion
analysis techniques, to interactively debug the planning knowledge base.
We describe these knowledge development tools and describe empirical results
documenting the usefulness of these tools.
Introduction
A key bottleneck in applying AI planning techniques to a real-world
problem is the amount of effort required to construct, debug, verify, and
update (maintain) the planning knowledge base. In particular, planning
systems must be able to compare favorably in terms of software lifecycle
costs to other means of automation such as scripts or rule-based expert
systems. An important component to reducing such costs is to provide a
good environment for developing planning knowledge bases. Despite this
situation, relatively little effort has been devoted to developing an integrated
set of tools to facilitate constructing, debugging, verifying, and updating
specialized knowledge structures used by planning systems.
While considerable research has focused on knowledge acquisition systems
for rule-based expert systems (Davis, 1979) , and object-oriented/inheritance
knowledge bases with procedures and methods (Gil and Tallis, 1995), little
work has focused on knowledge acquisition for specialized planning representations.
Notable exceptions to this statement are (DesJardins, 1994) which uses
inductive learning capabilities and a simulator to refine planning operators
and (Wang 1995) which uses expert traces to learn and a simulator to refine
planning operators. However, in many cases a simulation capability is not
available. In these situations the user needs assistance in causally tracing
errors and debugging from a single example. This assistance is sorely needed
to enable domain experts to write and debug domain theories without relying
on AI people. Furthermore, planning knowledge base maintenance is often
overlooked. Such tools are also invaluable in tracking smaller bugs, verifying
KB coverage ,
and updating the KB as the domain changes. While these tools can draw much
from causal tracking techniques used in rule-based systems (Davis, 1979),
there are several aspects of planning systems which differentiate them
from rule-based systems - their specialized representations and their temporal
reasoning capabilities. Two specialized representations for planning are
prevalent - task reduction rules and planning operators. These representations
as well as the most common constraints (ordering and codesignation constraints)
have evolved so that specialized reasoning algorithms must be adapted to
support debugging.
Many types of knowledge encoding errors can occur: incorrectly defined
preconditions, incorrectly defined effects, and incorrect variable specifications.
Invariably the end result is a mismatch between the planners model of the
legality of a plan and the model dictated by the domain (or domain expert).
Thus, the end symptoms of a knowledge base error can be broadly classified
into two categories.
Incorrect Plan Generation: This occurs when the planner is presented
a problem and generates a plan which does not achieve the goals in the
current problem context. In our experience, the current problem and faulty
solution can focus attention in debugging the flaw in the knowledge base.
By using the faulty plan to direct the debugging process, the user can
often focus on the incorrect link in the plan (faulty protection or achievement)
- allowing for rapid debugging.
Failure to Generate a Plan: This occurs when the planner is presented
with a solvable problem, but the planner is unable to find a solution.
In our experience this type of failure is far more difficult to debug.
This is because the user does not have a particular plan to use to focus
the debugging process. Thus, often a user would manually write down a valid
plan based on their mental model of the domain, and then trace through
the steps of the plan to verify that the plan could be constructed. Because
our experience has been that detecting and debugging failure-to-generate-a-plan
cases has been more difficult, our work focuses on: 1. verifying that a
domain theory can solve all solvable problems; and 2. facilitating debugging
of cases where the domain theory does not allow solution of a problem deemed
solvable by the domain expert.
This paper describes two types of tools developed to assist in developing
planning knowledge bases - static analysis tools and completion
analysis tools. Static analysis tools analyze the domain knowledge
rules and operators to see if certain goals can or cannot be inferred.
However, because of computational tractability issues, these checks must
be limited. Static analysis tools are useful in detecting situations in
which a faulty knowledge base causes a top-level goal or operator precondition
to be unachievable - frequently due to omission of an operator effect or
a typographical error.
Completion analysis tools operate at planning time and allow the planner
to complete plans which can achieve all but a few focused subgoals or top-level
goals. Completion analysis tools are useful in cases where a faulty knowledge
base does not allow a plan to be constructed for a problem that the domain
expert believes is solvable. In the case where the completion analysis
tool allows a plan to be formed by assuming goals true, the domain expert
can then be focused on these goals as preventing the plan from being generated.
The static analysis and completion analysis tools have been developed
in response to our experiences in developing and refining the knowledge
base for the Multimission VICAR Planner (MVP) (Chien, 1994a, 1994b) system,
which automatically generates VICAR image processing scripts from specifications
of image processing goals. The MVP system was initially used in December
1993, and has been in routine use since May 1994. The tools described in
this paper were driven by our considerable efforts in knowledge base development,
debugging, and updates to the modest sized knowledge base for MVP.
The remainder of this paper is organized as follows. Section 2 outlines
the two planning representations we support: task reduction rules and operators.
Section 2 also briefly describes how these representations are used in
planning. Section 3 describes static analysis rules for assisting in planning
KB verification and development. Section 4 describes completion analysis
rules for assisting in planning KB development.
VICAR Image Processing
We describe the static and completion analysis tools within the context
of the Multimission VICAR Planner system, a fielded AI planning system
which automates certain types of image processing
(Lavoie et. al., 1989). MVP uses both task reduction and operator-based
methods in planning. However, the two paradigms are separate, in that MVP
first performs task reduction (also called hierarchical task network or
HTN planning) and then performs operator-based planning. All of the task
reduction occurs at the higher conceptual level and the operator-based
methods at the lower level.
Consequently, MVP uses two main types of knowledge to construct image processing
plans (scripts):
decomposition rules - to specify how problems are to be decomposed
into lower level subproblems; and
operators - to specify how VICAR programs can be used to achieve lower
level image processing goals (produced by 1 above). These also specify
how VICAR programs interact.
These two types of knowledge structures are described in further detail
below.
A key aspect of MVP's integration of task reduction and operator-based
planning is that first task reduction is performed, then operator-based
planning. Because of the order in which these are performed, these two
types of knowledge can be checked separately.
Task Reduction Planning in
MVP
MVP uses a task reduction approach to planning. In a task reduction
approach, reduction rules dictate how in plan-space planning, one plan
can be legally transformed into another plan. The planner then searches
the plan space defined by these reductions. Syntactically, a task reduction
rule is of the form:
LHS RHS
GI = initial goal set/actions ...............GR= reduced goal set/actions
C2 = context ................................N = notes on decomposition
This rule states that a set of goals or actions GI can be reduced to
a new set of goals or actions GR if the set of constraints C0 is satisfied
in the current plan and the context C2 is satisfied in the current plan
provided the additional constraints C1 are added to the plan. C0 and C1
are constraint forms which specify conjuncts of constraints, each of which
may be a codesignation constraint on variables appearing in the plan, an
ordering constraint on actions or goal achievements in the plan, a not-present
constraint (which is satisfied only if the activity or goal specified does
not appear in the plan and never appeared in the derivation of the plan),
a present constraint (which is satisfied only if the activity or goal specified
did appear in the plan or derivation of the plan), or a protection constraint
(which specifies that a goal or set of goals cannot be invalidated during
a specified temporal interval. Skeletal planning (Iwasaki and Friedland,
1985) is a technique in which a problem is identified as one of a general
class of problem. This classification is then used to choose a particular
solution method. Skeletal planning in MVP is implemented in by encoding
decomposition rules which allow for classification and initial decomposition
of a set of goals corresponding to a VICAR problem class. The LHS of a
skeletal decomposition rule in MVP corresponds to a set of conditions specifying
a problem class, and the RHS specifies an initial problem decomposition
for that problem class.
MVP also uses decomposition rules to implement hierarchical planning.
Hierarchical planning (Stefik, 1981) is an approach to planning where abstract
goals or procedures are incrementally refined into more and more specific
goals or procedures as dictated by goal or procedure decompositions. MVP
uses this approach of hierarchical decomposition to refine the initial
skeletal plan into a more specific plan specialized based on the specific
current goals and situation. This allows the overall problem decomposition
to be influenced by factors such as the presence or absence of certain
image calibration files or the type of instrument and spacecraft used to
record the image. For example, geometric correction uses a model of the
target object to correct for variable distance from the instrument to the
target. For VOYAGER images, geometric correction is performed as part of
the local correction process, as geometric distortion is significant enough
to require immediate correction before other image processing steps can
be performed. However, for GALILEO images, geometric correction is postponed
until the registration step, where it can be performed more efficiently.
This decomposition-based approach to skeletal and hierarchical planning
in MVP has several strengths. First, the decomposition rules very naturally
represent the manner in which the analysts attack the procedure generation
problem. Thus, it was a relatively straightforward process for the analysts
to articulate and accept classification and decomposition rules for the
subareas which we have implemented thus far. Second, the notes from the
decomposition rules used to decompose the problem can be used to annotate
the resulting plan to make the output plans more understandable to the
analysts. Third, relatively few problem decomposition rules are easily
able to cover a wide range of problems and decompose them into much smaller
subproblems.
Operator-based Planning in
MVP
MVP represents lower level procedural information in terms of classical
planning operators. These are typical classical planning operators with
preconditions, effects, conditional effects, universal and existential
quantification allowed, and with codesignation constraints allowed to appear
in operator preconditions and effect conditional preconditions. For reasons
of space constraints the operator representation is only briefly described
here. (for a good description of a classical planning operator representation
similar to ours see (Pemberthy and Weld 1992)). Thus, an operator has a
list of parameter variables, a conjunctive set of preconditions, and for
each effect (which is a conjunct) there is a (possibly null) set of preconditions.
Operator
Parameters: variable*
Preconditions: Prec = Prop*
Effects: [Effecti = Prop* when Cpreci = Prop*]*
The above operator has the semantics that it can only be executed in
a state in which all of the preconditions Prec are true. And when executed,
for each effect set, if all of the conditional preconditions Cpreci are
true in the input state, the effect Effecti occurs and all of the effects
are true in the output state.
A description of the GALSOS operator is shown below.
operator GALSOS
:parameters ?infile ?ubwc ?calc
:preconditions
the project of ?infile must be galileo
the data in ?infile must be raw data values
:effects
reseaus are not intact for ?infile
the data in ?infile is not raw data values
missing lines are not filled in for ?infile
?infile is radiometrically corrected
the image format for ?infile is halfword
?infile has blemishes-removed
if (UBWC option selected) then ?infile is uneven bit wt. corrected
if (CALC option selected) then ?infile has entropy values calculated
An Overall Approach to Knowledge
Acquisition, Validation, and Refinement for MVP
During development of the MVP knowledge base, we used an iterative refinement
model in building the knowledge base. We began by eliciting representative
problem classes and used these to direct the knowledge elicitation - both
in terms of problem classes for the HTN rules and in terms of the causal
structure underlying the operators. Concurrent with the development of
this knowledge base, we attempted to elicit from expert analysts, declarative
descriptions of the coverage of each of these problem classes - in terms
of the legal combinations of goals and of initial states allowable.
When this knowledge base was relatively stable, it was tested against
a holdback set of problems not used during the original elicitation process.
This led to another round of refinement of the knowledge base and problem
class descriptions.
In the operational version of MVP, this definition of legal problem
classes is key. Before any problem is submitted to the planner from the
interface, it is first checked against these problem class constraints.
In the event that the submitted request does not pass the constraints,
it is not submitted to the planner - rather the user is notified that the
problem is not considered a valid request. If the user believes otherwise,
they can submit a bug report at this time.
If the problem is considered a valid one, then if the planner is correct
and sound, then the planner and knowledge base should be able to solve
the problem correctly. While the MVP planner is not complete (it cannot
backtrack across different decompositions in response to failures in operator-based
planning), in actual usage, we have not yet encountered a problem in which
this was the cause of a planner failure. Consequently, when the planner
(and KB) are unable to solve a problem (e.g., the planner cannot find a
solution either due to dead-ends in the search space or exceeding resource
bounds), a KB bug is assumed and a bug report is automatically submitted.
This bug report includes the requested goals, initial state, and image
files are logged. Similarly, if the planner generates an incorrect plan,
a bug report can be filed (manually) by the user. Figure 1
below graphically illustrates the acquisition and maintenance flows as
described.
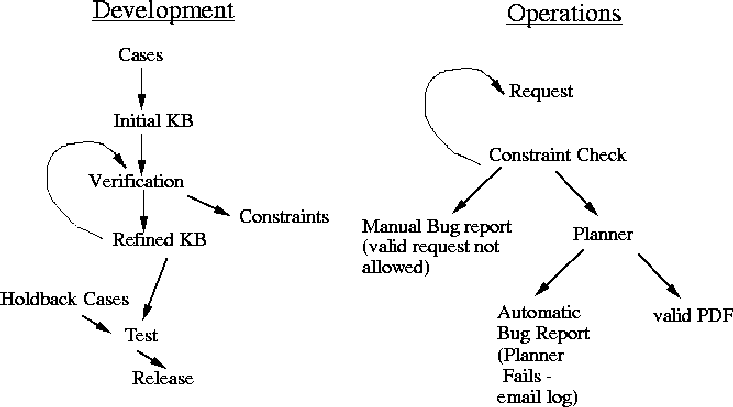
Figure 1: Initial Acquisition and Maintenance Processes for MVP
Planning Knowledge Base
Different Tool Types and
Representations
In order to facilitate this key process of knowledge acquisition and
refinement we have been developing a set of knowledge-base editing and
analysis tools. These tools can be categorized into two general types:
(1) static knowledge base analysis tools; and (2) completion analysis tools.
Because MVP uses two types of knowledge: decomposition rules and operator
definitions, each of these tools can be used with each of these representations.
Thus there are four types of tools:
static rule analysis tools;
static operator analysis tools;
completion rule analysis tools; and
completion operator analysis tools.
For each type of tool, it is possible to perform the analysis using
propositional or full predicate checking. In propositional analysis, all
actions and goals are considered optimistically only for the predicate
or goal name. For example, when considering whether an operator could achieve
a specific fact, "(radiometrically-corrected ?file1)", optimistic
treatment means that any effect or initial state fact with the predicate
"radiometrically-corrected" can be used. When considering whether
an effect , "(radiometrically-corrected ?file1)", deletes a protected
fact "(radiometrically-corrected ?file2)", one presumes that
the arguments to the predicate can be resolved such that the conflict does
not occur. Therefore the effect is not considered to delete the fact. The
propositional analysis is used as a fast checking component to catch simple
errors when debugging a knowledge base. The full static analysis is useful
but restricted to more batch-like analysis due to its computational expense.
Problem Spaces for Knowledge
Analysis
In our knowledge base development and refinement framework, the knowledge
base is divided into a set of problem spaces. A problem space consists
of a set of allowable sets of inputs and groundings. In the case of task
reduction, conceptually the planner is reducing a set of abstract activities
into more specific activities (although sometimes these specific activities
can be mapped . Hence, in task reduction, the inputs are non-operational
goals, groundings are operational goals, and the problem space corresponds
to a class of non-operational goal sets which can be reduced into operational
goals. In the case of operator-based planning, the planner is considering
which how to achieve goal state requirements using a particular set of
actions from certain initial states. In this case the problem space corresponds
to a class of goal states which can be achieved from a general class of
initial states. In both the task reduction and operator-based cases, the
inputs are specified in terms of logical constraints over goals and groundings
are specified in terms of a list of predicates which can be presumed true/operational.
These problem spaces represent a set of contexts in which the decomposition
planner or operator planner is attempting to solve a general class of problems.
Decomposing the overall problem solving process into these problem spaces
and analyzing each in isolation dramatically reduces the complexity of
the analysis process. Of course, this introduces the possibility that the
knowledge base analysis is flawed due to a poor problem decomposition.
Unfortunately, we know of no other way around this problem. While the tools
we describe are of assistance in analyzing the impact of the problem space
structure they do not directly assist in the definition of the problem
spaces - which is a direct burden on the user.
Within a single problem space only one of the HTN and operator-based
planner is being used. Hence in this case the system performing the analysis
is complete and correct so that inability to solve a problem is interpreted
as a flaw in the knowledge base.
Below in Figure 2 we list the
problem spaces used in the current MVP knowledge base. For each problem
space we describe the number of relevant planning operators, the number
of top-level input goals, and the typical number of plans searched in the
problem space.
Figure 2: Problem Space Information
Problem Space
# Of Operators
# Of Goals
Typical Search
local correction
15
7
60
automatic navigation
20
4
150
manual navigation
24
4
300
photometric correction
5
2
60
registration
13
5
110
mosaicking
4
3
325
touch ups
10
3
325
Static Analysis Tools
Static Analysis Tools for
Task Reduction Rules
Static analysis tools analyze the knowledge base to determine if pre-specified
problem-classes are solvable. The static analysis techniques can be used
in two ways: 1. fast run-time checking using propositional analysis (called
propositional static rule analysis); and 2. off-line knowledge-base analysis
to verify domain coverage (called full static rule analysis).
In the case of static rule analysis, the analysis process is to verify
that all legal sets of input goals can be reduced into operational goals/facts/tasks.
The set of allowable input goals is formally specified in terms of logical
constraints on a set of goals produced by the interface. Figure 3
describes the static rule analysis algorithm. Below we show a simplified
problem space description for the navigation problem space, and use this
to illustrate static rule analysis.
Input goals are all combinations of:
(attempt-to-FARENC ?files)
(automatch ?files)
(manmatch ?files)
(curve-verify ?files)
(display-automatch-residual-error ?files)
(display-manmatch-residual-error ?files)
(update-archival-sedr ?files)
Subject to the constraint that:
((attempt-to-FARENC ?files ?files) and (automatch ?files))
(curve-verify ?files) or (attempt-to-FARENC ?files)
(display-automatch-residual-error ?files) or (automatch ?files)
(display-manmatch-residual-error ?files) or (manmatch ?files)
Generally, the allowable sets of input goals are of the form "all
combinations of these 5 goals except that goal4 and goal3 are incompatible,
and that every time goal 2 is selected goal 1 must have parameter X and
so on.
The output legal set of goals/facts/tasks are defined in terms of a
set of operational predicates. For example, in the relative navigation
example used above has the operational predicates: construct-om-matrix,
and display-om-error.
This means that any goal/activity/fact produced using one of these predicates
is considered achieved. Static rule analysis runs the rules on these allowable
combinations and verifies that the decomposition rules cover the combinations
(this corresponds to exhaustive testing of the task reduction rules). As
described in Section 2.1, there are several types of constraints used in
the task reduction rules. Some of these constraints do not make sense for
a propositional analysis; how constraints are handled in the propositional
analysis is shown below.
Constraint Type
Propositional Case
Full Case
codesignation
ignored
tracked
not-present
ignored
tracked
present
propositional
trecked
ordering
tracked
tracked
protection
ignored
tracked
Table 1: Propositional vs. Full Constraint Handling
for each plan P' produced by reducing a goal in P using a task reduction
rule w. constraints as below
IF P' contains only operational goals return SUCCESS
ELSE add P' to Q and continue
The principal difference between the propositional and non-propositional
cases is that when predicates are transformed to the propositional case,
constraint resolution optimistically presumes variable assignments will
remove conflicts. For example, consider the plan and reduction rules shown
below.
Reduction Rule1: if present: (bar ?a) not-present: (foo ?b)
Reduction Rule2: if present: (bar ?a) (foo ?a)
In the propositional case, both rule1 and rule2 apply to both plan1 and
plan2. In the full case, rule 1 does not apply either plan1 or plan2. In
the full case rule2 applies to plan1 but does not apply to plan2. Note
that in the propositional case, in order to presume that variables resolve
optimistically, the analysis procedure need not compute all possible bindings.
Rather, the analysis procedure resolves present constraints by presuming
matching if the predicate matches and by ignoring not- present constraints
(and others as indicated above). To further illustrate, consider the following
example from the MVP domain. The input goals, relevant decomposition rules,
and operational predicates are shown below.
In both the propositional and full static rule analysis cases both rules
would apply in the analysis. Thus, both analyses would indicate that the
input goals can be reduced into operational facts/activities.
Static Analysis Tools for
Operator-based Planning
The static analysis techniques can also be applied to the MVP's operator-based
planner component. This is accomplished by generalizing the planning algorithm.
Again, as with the static rule analysis, the static operator analysis is
considering a general class of problems defined by a problem space. As
with the static rule analysis, a problem space defines an allowable set
of goals and a set of operational predicates which are assumed true in
the initial state.
In the propositional static operator analysis case, in order to treat
the domain theory optimistically, we must assume that all protection interactions
can be resolved by variable assignments. Because of the absence of protection
constraints, the propositional operator static analysis corresponds to
the propositional rule-based static analysis. An operator with preconditions
P and effects E maps onto a rule with LHS P and RHS E. Conditional effects
extend analogously.
The non-propositional static analysis case is handled by modifying a
standard operator-based planner. The planner is changed by adding an achievement
operation corresponding to presuming any operational fact is true in the
initial state. We are currently investigating using more sophisticated
static analysis techniques to detect more subtle cases where goals are
unachievable (Etzioni, 1993, Ryu and Irani, 1992). The full (e.g. non-propositional)
operator static analysis algorithm is shown below in Figure 4.
The * on Step 3 indicates that this is the key modification to a standard
operator-based planning algorithm to perform static operator analysis.
initialize plan queue Q to {(goals=input, constraints={})}
select a plan P from Q
for each plan P' produced by achieving a goal G using the following
methods:
1. use an existing operator in the plan to achieve G
2. add a new operator to the plan to achieve G
3.* if the goal is operational assume it true in the initial state
resolve conflicts in P' (protections)
IF P' has no unresolved conflicts and no unachieved goals
THEN return SUCCESS
ELSE add P' to Q and continue
Figure 4: Static Operator Analysis Algorithm
Figure 5 shows the subgoal
tree generated by performing full static analysis on the operator planner
problem space defined by: Input Goals: (compute-om-matrix ?fl manmatch)
(update-archival-sedr ?fl manmatch) and Operational Predicates: project,
initial-predict-source.
The second type of knowledge base development tool used in MVP is the
completion analysis tool. In many cases, a knowledge engineer will construct
a domain specification for a particular VICAR problem, test it out on known
files and goal combinations. Two possible outcomes will occur. First, it
is possible that the domain specification will produce an invalid solution.
Second, it is possible that the planner will be unable to construct a solution
for a problem that the expert believes is solvable.
In the case that the planner constructs an invalid solution, the knowledge
engineer can use the inconsistent part of the solution to indicate the
flawed portion of the domain theory. For example, suppose that the planner
produces a plan consisting of steps ABCD, but the expert believes that
the correct plan consists of steps ABCSD. In this case the knowledge engineer
can focus on the underlying reason that S is necessary. S must have had
some purpose in the plan. It may be needed to achieve a top-level goal
G or a precondition P of A, B, or C. Alternatively, if the ordering of
operators or variable assignments is not valid in the produced plan, the
knowledge engineer can focus on the protection or other constraint which
should have been enforced.
The second possibility is that the domain specification fails to allow
the desired solution. For example, the expert believes that the plan ABCD
should achieve the goals, but the planner fails to find any plan to achieve
the goals. In this case, detecting the flawed part of the knowledge base
is more difficult, because it is difficult to determine which part of the
domain specification caused the desired output plan to fail. In manually
debugging these types of problems, the knowledge engineer would write out
by hand the plan that should be constructed. The knowledge engineer would
then construct a set of problems, each of which corresponded to a subpart
of the failed complete problem. For example, if a failed problem consisted
of achieving goals A, B, and C, the knowledge engineer might try the planner
on A alone, B alone, and C alone, to attempt to isolate the bug to the
portion of the knowledge base corresponding to A, B, or C, correspondingly.
Completion analysis tools partially automate this tedious process of
isolating the bug by constructing subproblems. The completion analysis
tools allow the decomposition or operator-based planner
to construct a proof with assumptions that a small number of goals or subgoals
can be presumed achievable (typically only one or two).
By seeing which goals, if assumable, make the problem solvable, the user
gains valuable information about where the bug lies in the knowledge base.
For example, if a problem consists of goals A, B, and C, and the problem
becomes solvable if B is assumed achievable, the bug is likely to be in
the portion of the knowledge base relating to the achievement of B. Alternatively,
if the problem is solvable when either B or C is assumed achievable, then
the bug likely lies in the interaction of the operators achieving B and
C. The completion analysis tool is used by running the modified planner
algorithm until either: 1. a resource bound of the number of plans expanded
is reached; or 2. there are no more plans to expand. The completion analysis
algorithm for the reduction planner is shown below in Figure 6
.
for each plan P' produced by reducing P using a task reduction rule
IF the constraints in P' are consistent
IF P' contains only operation goals/activities
THEN add P' to SOLUTIONS
ELSE add P' to Q and continue
ELSE discard P'
for each plan P' produced by presuming the current goal achieved/operational
IF P' contains only operation goals/activities
THEN add P' to SOLUTIONS
ELSE increment NumberOfAssumptions(P')
IF NumberOfAssumptions(P') <= bound
THEN add P' to Q
Figure 6: Completion Analysis for Reduction Rules
In the operator-based planner, completion analysis is permitted by adding
another goal achievement method which corresponds to assuming that the
goal is magically achieved. The completion analysis operator planner is
then run until either 1. a resource bound of the number of plans expanded
is reached; or 2. there are no more plans to expand. All solutions found
are then reported back to the user to assist in focusing on possible areas
of the domain theory for refinement. The basic completion analysis algorithm
for the operator planner is shown below in Figure 7.
The * on Step 4 indicates the principal modification to the standard operator-based
planning algorithm made to perform operator-based completion analysis.
for each plan P' produced by achieving a goal using the following methods:
1. use existing operator in the plan to achieve the goal
2. add a new operator to the plan to achieve the goal
3. use the initial state to achieve the goal
4.* if the number of goals already assumed in P is less than the bound
assume the goal true using completion analysis;
the # of assumptions in the new plan is 1+ in P;
resolve conflicts in P' (protections);
IF P' has no unresolved conflicts and has no unachieved goals
THEN add P' to SOLUTIONS
ELSE add P' to Q and continue
Figure 7: Completion Analysis for Operator Planner
The main drawback of the completion analysis tools is that they dramatically
increase the size of the search space. Thus, with the completion analysis
tools, we provide the user with the option of restricting the types of
goals that can be presumed true. Currently the user can restrict this process
in the following ways:
allow only top-level (problem input) goals to be assumed;
allow only goals appearing in a specific operators preconditions to
be assumed;
allow goals relating to an operator (appearing in its precondition
or effects) to be assumed; and
only allow certain predicates to be assumed.
Thus far, we have found these restriction methods to be fairly effective
in focusing the search. Note that allowing certain goals to be presumed
true corresponds to editing the problem definition (or domain theory) numerous
times and re-running the planner. For example, allowing a single top-level
goal to be assumed true for a problem with N goals corresponds to editing
the problem definition n times, each time removing one of the top-level
goals and re-running the planner each time. Allowing a precondition of
an operator to be suspended corresponds to running the planner on the original
problem multiple times, each time with a domain theory that has one of
the operator preconditions removed. Manually performing this testing to
isolate an error quickly grows tiresome. Furthermore, if multiple goals
are allowed to be suspended, the number of edits and runs grows combinatorially.
The completion analysis tools are designed to alleviate this tedious process
and to allow the user to focus on repairing the domain theory. As a side
effect, running the planner only once is also computationally more efficient
than running the planner multiple times. This is because the planner need
explore portions of the search space unrelated to the suspended conditions
fewer times.
Thus, the completion analysis techniques are generally used in the following
manner. MVP automatically logs any problems unsolvable by the task reduction
planner (unreducable) or operator-based planner (no plan found). The user
then specifies that one of the top-level goals may be suspended (any one
of the top-level goals is a valid candidate - the planner tries each in
turn. The completion planner then finds a plan which solves all but one
of the top-level goals - focusing the user on the top-level goal which
is unachievable. The user then determines which operator O1 that should
be achieving the goal, and specifies that the completion planner may consider
suspending preconditions of O1. The completion analysis planner runs and
determines which precondition P1 of O1 is preventing application of this
operator. Next, the user determines which operator O2 should be achieving
this precondition P1 of O1, and the process continues recursively until
the flawed operator is found. For example, it may be that a protection
cannot be enforced, thus preventing a precondition P1 from being achieved.
In this case, suppose another operator O2 should be able to achieve P1.
But suspending its preconditions does not allow the problem to be solved.
This might hint to the knowledge engineer that the problem is in the protection
of P1 from O2 to O1. Alternatively, it may be that no operator has an effect
that can achieve P (perhaps the knowledge engineer forgot to define the
effect or operator). Or that the effect has a different number of arguments,
or arguments in a different order, or arguments of a different type. These
types of bugs can be easily detected once the bug has been isolated to
the particular operator. Another possibility is that a conditional effect
that should be used has the wrong conditional preconditions. Again, once
the bug has been traced to a particular operator, the debugging process
is greatly simplified.
In order to further explain how the completion analysis tools are used,
we now describe a detailed example of how the completion analysis tools
are used. The graph below in Figure 8
illustrates this process from an actual debugging episode which occurred
in the development of a portion of the planning knowledge base
relating to a problem called relative navigation .
Each of the following steps in the debugging process is labeled P if the
planner performed the step; U if the user/knowledge engineer performs the
step; or C if the completion analysis tool performs the step.
1. (P) The planner is unable to solve the original problem.
2. (U) The user initiates the debugging process by invoking the operator-based
completion analysis tool specifying that one top-level goal may be suspended.
3. (C) The completion planner constructs a plan achieving all of the
goals but the top-level goal of (compute-om- matrix ?om-matrix ?file-list
?file-list).
4. (U) The user then determines that the OMCOR2 operator should have
been able to achieve the goal (compute-om-matrix ?om-matrix ?file-list
?file-list). The user then continues the debugging process by invoking
the completion analysis tool specifying that a precondition of the OMCOR2
operator may be suspended.
5. (C) In response to the user request, the completion planner finds
a plan achieving all goals except the OMCOR2 precondition (tiepoint-file
?tp ?file-list manmatch).
6. (U) The user then determines that the precondition (tiepoint-file
?tp ?file-list manmatch) should be achieved by the MANMATCH operator, and
invokes the operator completion analysis tool allowing suspension of one
of the preconditions of the MANMATCH operator.
7. (C) The completion planner then finds a plan achieving all goals
but the precondition (refined-overlap-pairs ?rop- file ?file-list) of the
operator MANMATCH.
8. (U) The user then determines that the precondition (refined-overlap-pairs
?rop-file ?file-list) should have been achieved by the EDIBIS operator
and invokes the operator completion analysis tool allowing suspension of
an EDIBIS precondition.
9. (C) The completion planner finds a plan achieving all goals but the
precondition (crude-overlap-pair ?cop-file ?file-list) of EDIBIS.
10. (U) The user then determines that this precondition (crude-overlap-pair
?cop-file ?file-list) should have been achieved by the MOSPLOT-construct-crude-nav-file.
This results in another invocation of the completion analysis tool allowing
suspension of a precondition for MOSPLOT-construct-crude-nav-file.
11. (C) The completion analysis tool then finds a plan achieving all
goals but the precondition (latlon ?mf ?lat ?lon) for the operator MOSPLOT-construct-crude-nav-file.
12. (U) At this point, the user notices that the constructed plan for
achieving the goals has assumed the instantiated goal (latlon &middle-file
?lat ?lon). This immediately indicates the error to the user because the
user is expecting a file name as the second argument of the latlon predicate
.
Figure 8: Subgoal Graph for Completion Analysis Debugging
Unfortunately, we have as of yet not been able to determine any heuristics
for controlling the use of these completion tools that allows for more
global search or allows for less user interaction. However, in their current
form, the completion analysis tools have proved quite useful in debugging
the MVP radiometric correction and color triplet reconstruction knowledge
base.
Impact of Debugging
In order to quantify the usefulness of the completion analysis tools,
we collected data from a 1 week phase of domain theory development for
the relative navigation portion of the domain theory. During this week,
we identified 22 issues raised by a domain expert analyst which at first
guess appeared to be primarily in the decomposition rules or operators.
For 11 of these 22 problems (selected randomly) we used the debugging tools
in refining the domain theory. For the other 11 problems we did not use
the debugging tools. When tools were allowed, we estimated that the tools
were applicable in 7 out of the 11 problems. These 7 problems were solved
in an average of 10 minutes each. The other 4 took on average 41 minutes.
The total 11 problems where the tools were used took on average 21 minutes
each to correct. In the 11 problems solved without use of the tools, after
fixing all 11 problems, we estimated that in 6 out of the 11 problems that
the debugging tools would have helped. These 6 problems took on average
43 minutes each to solve. The remaining 5 problems took on average 40 minutes
to solve. The second set of 11 problems took on average 42 minutes to solve.
Set
Tools
Average
Tools
Average
Overall Average
Tool
7/11
10 min.
4/11
41 min.
21 min.
No Tool
6/11
43 min.
5/11
40 min.
42 min.
Table 2: Empirical Impact of Completion Analysis Tools
Discussion
One area for future work is development of explanation facilities to
allow the user to introspect into the planning process. Such a capability
would allow the user to ask such questions as "Why was this operator
added to the plan?" and "Why is this operator ordered after this
operator?", which can be answered easily from the plan dependency
structure. More difficult (but also very useful) questions are of the form
"Why wasn't operator O2 used to achieve this goal?" or "Why
wasn't this problem classified as problem class P?". We are currently
investigating using completion analysis tools to answer this type of question.
The completion analysis techniques are related to theory refinement techniques
from machine learning (Mooney and Ourston, 1994, Ginsberg et. al., 1988).
However, these techniques presume multiple examples over which to induce
errors. Additionally, reasoning about planning operators requires reasoning
about the specialized planning knowledge representations and constraints.
This paper has described two classes of knowledge base development tools.
Static analysis tools allow for efficient detection of certain classes
of unachievable goals and can quickly focus user attention on the unachievable
goals. Static analysis techniques can also be used to verify that domain
coverage is achieved. Completion analysis tools allow the user to quickly
focus on which goals (or subgoals) are preventing the planner from achieving
a goal set believed achievable by the knowledge base developer. These tools
are currently in use and we have presented empirical evidence documenting
the usefulness of these tools in constructing, maintaining, and verifying
the MVP planning knowledge base.
Acknowledgements
This work was performed by the Jet Propulsion Laboratory, California
Institute of Technology, under contract with the National Aeronautics and
Space Administration. The author would also like to acknowledge the contributions
of other past and present members of the MVP team: Helen Mortensen, Forest
Fisher, Todd Turco, Christine Ying, Shouyi Hsiao, Darren Mutz, Alex Gray,
Joe Nieten, and Jean Lorre.
References
(Chien, 1994a) Chien, S., Using AI Planning Techniques to Automatically
Generate Image Processing Procedures: A Preliminary Report. Proceedings
of the Second International Conference on AI Planning Systems, Chicago,
IL, June 1994, pp. 219-224.
(Chien, 1994b) Chien, S., Automated Synthesis of Complex Image Processing
Procedures for a Large-scale Image Database. Proceedings of the First IEEE
International Conference on Image Processing, Austin, TX, Nov 1994, Vol
3, pp. 796-800.
(Chien and Mortensen, 1996) Chien, S., Mortensen, H. Automating Image
Processing for Scientific Data Analysis of a Large Image Database. IEEE
Transactions on Pattern Analysis and Machine Intelligence, (18) 8 pp. 854-859
August 1996.
(Chien et. al. in preparation) Chien, S., Estlin, T., Wang, X., Govindjee,
A., Hill, R., Automated Generation of Antenna Operations Procedures: A
Knowledge-based Approach. Submitted to Telecommunications and Data Acquisition.
(Chien et. al., 1996) Chien, S., Estlin, T., Wang, X., Hierarchical
Task Network and Operator-based Planning: Competing or Complementary. JPL
Technical Document D-13390 Jet Propulsion Laboratory, California Institute
of Technology, January 1996.
(Davis, 1979) Davis, R., Interactive Transfer of Expertise: Acquisition
of New Inference Rules. Artificial Intelligence 12 (2) 1979, pp. 121-157.
(DesJardins, 1994) DesJardins, M., Knowledge Development Methods for
Planning Systems. Working Notes of the AAAI Fall Symposium on Learning
and Planning: On to Real Applications, New Orleans, LA, Nov 1994, pp. 34-40.
(Etzioni, 1993) Etzioni, O., Acquiring Search Control Knowledge via
Static Analysis. Artificial Intelligence, 62 (2) 255-302, 1993.
(Gil and Tallis 1995) Gil, Y., Tallis, M., Transaction- based Knowledge
Acquisition: Complex Modifications Made Easier. Proceedings of the Ninth
Knowledge Acquisition for Knowledge-based Systems Workshop, 1995.
(Ginsberg et. al. 1988) Ginsberg, A., Weiss, S., Politakis, P., Automatic
Knowledge Based Refinement for Classification Systems. Artificial Intelligence,
35 pp. 197-226, 1988.
(Iwasaki and Friedland, 1985) Iwasaki, Y., Friedland, P., The Concept
and Implementation of Skeletal Plans. Automated Reasoning 1, 1 (1985),
pp. 161-208.
(Lansky, 1993) Lansky, A., Localized Planning with Diverse Plan Construction
Methods. TR FIA-93-17, NASA Ames Research Center, June 1993.
(Lavoie et al. 1989) LaVoie, S., Alexander, D., Avis, C., Mortensen,
H., Stanley, C., Wainio, L., VICAR User's Guide, Version 2, JPL Internal
Doc.D-4186, Jet Propulsion Laboratory, California Inst. of Tech., Pasadena,
CA, 1989.
(O'Keefe and O'Leary, 1993) O'Keefe, R., O'Leary, D., Expert System
Verification and Validation: A Survey and Tutorial. AI Review, 7:3-42,
1993.
(Mooney and Ourston, 1994) Mooney, R., Ourston, D., A Multistrategy
Approach to Theory Refinement. in Machine Learning: A Multistrategy Approach,
Vol. IV, R.S. Michalski and G. Teccuci (eds.), pp.141-164, Morgan Kaufman,
San Mateo,CA, 1994.
(Pemberthy and Weld 1992) Pemberthy, J., Weld, D., UCPOP: A Sound Complete,
Partial Order Planner for ADL. Proceedings of the Third International Conference
on Knowledge Representation and Reasoning, October 1992, pp. 103-114.
(Ryu and Irani, 1992) Ryu, K., Irani, K., Learning from Goal Interactions
in Planning: Goal Stack Analysis and Generalization. Proceedings of the
1992 National Conference on Artificial Intelligence (AAAI92), pp. 401-407.
(Stefik, 1981) Stefik, M., Planning with Constraints (MOLGEN: Part 1).
Artificial Intelligence 16, 2(1981), pp. 111-140.
(Wang, 1995) Wang, X., Learning by observation and practice: An incremental
approach for planning operator acquisition. In the Proceedings of the 1995
International Conference on Machine Learning (ML95).
About this document ...
Knowledge Acquisition, Validation, and Maintenance in a Planning
System for Automated Image Processing
The command line arguments were: latex2html-split 0 kaw96.tex.
The translation was initiated by Steve Chien on Mon Oct 7 11:06:57 PDT
1996
...coverage
For work in verifying rule-based systems - see (O'Keefe and O'Leary,
1993). For work on rule base refinement using training examples (the analogue
of a simulator for planning KB refinement) see (Ginsberg et. al., 1988).
...processing
We only briefly describe the MVP application due to space constraints.
For further information on this application area, MVP architecture, and
knowledge representation see (Chien, 1994a, 1994b, Chien and Mortensen,
1996).
...level
MVP first uses task reduction (Lansky, 1993) planning techniques to
perform high level strategic classification and decomposition of the problem
then uses traditional operator-based (Pemberthy and Weld, 1992) planning
paradigms to plan at the lower level
...separately.
A more recently developed planner (Chien et al, in preparation, Chien
et al, 1996) completely integrates these two planning paradigms. While
natural extensions of static and completion analysis to this integrated
planning approach exist, we have not as of yet explored such possibilities.
...planner
In the completion analysis for both the reduction planner and the operator-based
planner there are choice points in the search in ordering plans in the
search queue. In both cases, we use standard heuristics based on the number
of outstanding goals and plan derivation steps so far. However, the static
analysis techniques would work with any appropriate heuristic for this
search choice.
...two)
The number of goals assumable is kept small because allowing the planner
to assume goals dramatically increases the search space for possible plans.
It effectively adds 1 to the branching factor of every goal achievement
node in the search space for the plan
...base
Note that this is the operator portion of the knowledge base relating
directly to the task reduction rules shown in the example for static rule
analysis.
...navigation
For the interested reader, navigation of the image is the process of
determining the appropriate transformation matrix to map each pixel from
the 2-dimensional (line, sample) of the image space to a 3-dimensional
(x,y,z) of some coordinate object space (usually based on the planet center
of the target being imaged). Relative navigation corresponds to the process
when determining the absolute position of each point is difficult to compute
so that the process focuses on determining the correct positions of each
point relative to other points in related images.
...predicate
This is because the latlon goal is designed to refer to a specific
image file (e.g., 1126.IMG). Correspondingly, the planning operators that
had been defined to acquire information such as latlon presumed actual
file names. Unfortunately, &middle-file refers to a VICAR variable
which will be bound to an actual file name only at the time that the VICAR
script is run (i.e. when the plan is executed). Thus, the bug lies in the
mismatch between this precondition and the operators which can determine
latlon information for a file. This bug was then fixed by defining operators
which could utilize the VICAR variable information at runtime and perform
the correct steps to compute the needed latlon information.
,
and updating the KB as the domain changes. While these tools can draw much
from causal tracking techniques used in rule-based systems (Davis, 1979),
there are several aspects of planning systems which differentiate them
from rule-based systems - their specialized representations and their temporal
reasoning capabilities. Two specialized representations for planning are
prevalent - task reduction rules and planning operators. These representations
as well as the most common constraints (ordering and codesignation constraints)
have evolved so that specialized reasoning algorithms must be adapted to
support debugging. 
