School of Computer Science and Engineering,
University of New South Wales, Sydney 2052, Australia
email compton@cse.unsw.edu.au
G. Edwards
Western Diagnostics Pathology, Perth, Australia
B. Kang
Department of Computer Science, Hoseo University, Korea
The CYC project is one attempt at a solution to this problem (Lenat & Feigenbaum 1991). CYC is an attempt to build a knowledge base of sufficient consensus or common sense knowledge so that specific KBS built on top of CYC will be able to fall back on common sense in a human like fashion and avoid stupid errors. CYC is aimed specifically at errors like the pregnant male syndrome where common sense, if it was available, would help the system reach a correct conclusion.
Apart from the problems of common sense that arise, there are also issues of brittleness within the domain itself. Even with apparently fairly complete systems, stupid errors are liable to be made. For an example see (Compton, et al. 1989). Despite the availability of techniques to check if a knowledge base is complete(Preece, et al. 1992), in practice this is not very useful. Most interesting practical systems cover a huge space of possible data patterns, so that an expert will not be asked about all of them in building a system. The vast majority of these data patterns may never occur in practice (Colomb & Sienkiewicz 1996) and experience in dealing with experts suggests that their responses become rather speculative when dealing with data patterns outside their experience (Compton & Jansen 1990).
As will be discussed below we have been developing approaches to knowledge acquisition based on correcting errors as they occur, so that the knowledge base is developed whilst the system is in actual use and errors are detected. Clearly for such a system it would be very attractive if the system knew when it was dealing with situations beyond its present competence and was able to request further knowledge acquisition. However, it should be noted that such a feature is perhaps even more desirable for conventional systems. These are systems where we have attempted to make the knowledge as complete as possible before the system is put into use. Although a high level of performance is probably verified before the system is deployed, all this means is that the system is likely to make few errors; but what these are, when they will occur and their significance is generally not known. We are still a long way from fully verified and validated systems.
The aim of the present work is to develop an approach whereby a KBS will realise that a case it is dealing with is beyond its competence and will request help. For a system with an apparently high level of performance this will be an occasional warning that the system's output needs checking. With a system designed for incremental development whilst in actual use, the system will be responsible for requesting knowledge acquisition as needed.
We have previously attempted to exploit the particular structure of the incremental knowledge acquisition method, Ripple Down Rules (RDR), to suggest when a conclusion for a case is incorrect (Kang & Compton 1992). This approach was based on the idea that the KBS to processes a case and reaches a conclusion, but that the system's knowledge is checked to see if knowledge in another context, not reached by the case, may actually satisfy the case and thereby suggest that the conclusion arrived at may be wrong. The motivation was to capture the human notion that a certain conclusion seems appropriate, but that there is just something about the case that reminds us of some other quite different context so we have some doubt about the more immediately obvious conclusion. Although this approach is useful and has some interesting cognitive features and is being developed further, it depends on other knowledge already in the knowledge base and so does not satisfy the requirement for a system that will warn when a case is outside the system's experience.
The approach we have now developed and which is evaluated here is based simply on the idea of keeping a sufficient record of all cases seen by the system and warning about any cases different from those previously seen. We use the term "prudence" to describe this behaviour of issuing a warning every time a case is in some way unusual. We have previously evaluated this approach by rebuilding 600 rules of a medical expert system by hand (Edwards, et al. 1995). The results of this initial study were very promising in that as the knowledge based was developed, every error the system made, that is every case where further knowledge acquisition was required, was correctly warned about. The system correctly prompted for all knowledge acquisition. However, the warnings were unnecessary in some 40% of cases. This seemed to be a major advance in that normally such a system would require all output to be checked, whereas with the prudence feature included only 40% of cases had to be checked. More importantly, no undetected errors were made.
In the work described here we have carried out a larger scale evaluation based on using a simulated expert for knowledge acquisition enabling a number of studies based on different domains. The essential idea is that using a simulated expert, despite the limitations and non-human nature of its expertise, enables the performance of a system to be evaluated on large data sets, where this would be very difficult to organise with human experts. We have previously used this approach to evaluate the efficiency of the RDR methodology (Compton, et al. 1995).
The strategy of warning every time a case is different from those previously seen by the system is very simple. However, it overcomes the problem of dealing with parts of the state space where cases do not occur or occur extremely rarely. With the approach of providing warnings one does not need to develop rules for these parts of the state space; the rules are adequate for the data patterns that generally occur and for the rare occasions when a novel pattern occurs these are warned about so that other more expert advice can be sought.
All the data in these studies are in attribute-value form. Associated with each rule path and also with each conclusion we keep a set of the values seen for each attribute. If the value for an attribute for a case being processed is not already included in the list of values for that attribute a warning is given to check the conclusion for the case. If the conclusion is then accepted, the list of values for the attribute stored with that rule are updated with the new value. If the conclusion is wrong and a new rule is added, the values for the attributes for this particular case become the initial set of acceptable values for the attributes associated with the new rule. Numerical data is taken as a special case and instead of keeping the actual values, the range of values seen is kept so that a value for an attribute in a case may a new maximum or minimum.
The data requires some consideration before this technique can be used and any datum that is unique to the case, such as an identification number, needs to be removed. Otherwise, all cases will be warned about. Apart from such data all other attributes are considered; both attributes that are known to be relevant to the problem domain and those which may not be so relevant. One assumes that the data that constitute the case are broadly relevant to the task otherwise they would not have been collected, but not all the data will be immediately relevant to the conclusions under consideration. For example, in a medical KBS one may be building a KBS for a particular diagnostic sub-domain. There will almost certainly be other laboratory and clinical information available, which although not apparently relevant to the domain, may be relevant under some circumstances.
A limitation of the method chosen is that we are implicitly assuming that all attributes are independent and so the values can be considered independently. As will be seen, this is a good first approximation, but is not appropriate if one requires a system guaranteed to warn for all unusual cases. Alternative strategies will be discussed.
The key area that has evolved in RDR is how to organise distinguishing between cases. In initial studies focussed on classification tasks where only a single classification per case is required, rules were linked in a binary tree structure and a single case was stored with each rule. When a conclusion had to be corrected a new rule was added at the end of the inference path through the tree giving the wrong conclusion. The rule had to then distinguish between the new case and the case associated with the rule that gave the wrong conclusion (Compton & Jansen 1990). The major success for this approach has been the PEIRS system, a large medical expert system for pathology laboratory report interpretation built by experts without the support of a knowledge engineering (Edwards, et al. 1993). It was also built whilst in routine use. Despite the fact that knowledge is added in random order, simulation studies have shown that knowledge bases produced by correcting errors as they occur are at least as compact and accurate as those produced by induction(Compton, et al. 1995; Compton, et al. 1994).
More recently we have developed RDR to deal with classification tasks where multiple independent classifications are required (Kang 1996; Kang, et al. 1995). This approach allows for n-ary trees, but is most simply understood in terms of a flat rule structure, where all rules are evaluated against the data. When a new rule is added, all cases associated with the KBS could reach this rule, so that the rule must distinguish between the present case and all the stored cases. In the approach developed, the expert is required firstly to construct a rule which distinguishs between the new case and one of the stored cases. If other stored cases satisfy the rule, further conditions are required to be added to exclude a further case and so on until no stored cases satisfy the rule. Surprisingly the expert provides a sufficiently precise rule after two or three cases have been seen (Kang, et al. 1995). Rules which prevent an incorrect conclusion by providing a null conclusion are added in the same way. The MCRDR system produces somewhat better knowledge bases than RDR even for single classification domains, probably because more use is made of expertise rather than depending on the KB structure (Kang 1996).
From an RDR perspective, the important difference between construction and classification is that components of the solution may depend on each other as well as the data initially provided to the system. To avoid an explosion in knowledge this is normally handled by some sort of inference cycle so that as conclusions are reached they are added to working memory and further conclusions can be arrived at. To control the inference and arrive at a solution some further problem solving method is used or at least implicit, such as "propose and revise" (Zdrahal & Motta 1994). This description probably seems extremely simplistic since some sort of cyclic inference probably underlies most expert systems. However, the lack of an inference cycle in RDR is precisely what makes it relatively simple to ensure that the same pathways are used by the same cases during system development. The challenge for RDR for construction tasks is to deal with the apparent requirement of a cycle for these tasks.
Speculating, it seems to us that the general availability of cyclic inference has been one of the reasons why a knowledge level analysis of KBS became so necessary (as well as being a major source of maintenance problems). If one stays at the inference level, classification tasks do not actually need an inference cycle. Both RDR and MCRDR require only a single pass through a KB and more generally it has been shown that all classification KBS can be reduced to a single pass decision table (Colomb & Chung 1990). It is only when one moves to construction tasks that an inference cycle seems necessary to avoid repeating the same knowledge to deal with every possible data profile. Construction tasks are precisely those tasks where parts of the conclusion affect each other suggesting sequential inference.
We should digress at this stage to comment on heuristic classification (Clancey 1985). Clancey's heuristic classification model includes: abstracting the data, reaching broad conclusions and then refining the conclusions. Although this is generally implemented in some sort of cyclic inference, there is no intrinsic requirement to do this. The key reason for the two intermediate stages in heuristic classification is to maximise the utility of the knowledge provided by experts. If knowledge is simply links between specific data in a case and specific conclusions, then each chunk will be too particular and too much knowledge will need to be added. There is clearly some advantage in providing rules which refer to ranges or clusters of data, so that rules will cover a range of cases. Clearly also, to explain their knowledge, experts discuss broad groups of classifications and how combinations of these determine the final specific conclusion. The RDR approach accepts the advantage of data abstraction, but finds the maintenance and knowledge engineering difficulties of appropriately managing reasoning with broad categories outweighs its advantages. Certainly the third stage is important for explanation, but one can speculate whether it would have been seen as intrinsic to classification inference if cyclic inference had not been available.
With respect to an RDR approach to configuration, the particular cyclic method, whether propose and revise in one of its many variants or some other method is of little importance. There is essentially some sort of inference cycle and some way of controlling this and deciding when and how it should terminate. One can consider the case (Breuker 1994) or Clancey's Situation Specific Model (Clancey 1992) gradually being fleshed out as inference proceeds. RDR for classification tasks not only ensures that cornerstone cases keep having the same conclusion, it also ensures that the same inference sequence is followed. Kang (1996) has suggested how this might be achieved for configuration tasks. When a new rule is added to the KB, the case would also be stored. However the case would be stored in conjunction with all the rules that were satisfied in reaching the particular conclusion given. The case would be stored with each rule partially filled out to the same level as when that rule was evaluated. In the same way as MCRDR, when a new rule is added it would required to distinguish between the new case and the cases stored whether complete or partially filled out. This should again ensure incremental development of the KBS in that the cornerstone cases should still follow exactly the same inference sequence to reach the same conclusions as the knowledge base develops. This would also appear to be quite independent of the problem solving method used. The problem solving method controls how the system proceeds to the next inference cycle while the RDR system ensures that each inference cycle processes the cornerstone cases in the same way as previously. It would be critical in this approach that the problem solving or inference method not be changed during development as this may alter rule pathways. However, in practice most KBS probably satisfy this constraint because of the way in which knowledge is organised to control inference (Clancey 1992). Experiments are under way to test the feasibility of this approach.
The studies below are all based on single classification RDR but we see no reason why the approach cannot be used with multiple classification or construction RDR since the critical issue is to ensure that cases follow the same rule pathway. For a conventional KBS prudence perhaps could be readily developed, if it was guaranteed there would be no further changes to the KB. In this case a profile could be stored with every rule which was updated every time the rule fired. However there is almost a contradiction in using prudence to warn when the system may be making a mistake, but not allow the possibility of fixes to the KB. It may be possible to use validation and verification or related techniques to ensure incremental changes to the KB and thereby continue to use the previous profile information. However this is probably just a more difficult way of carrying out an RDR equivalent change. This will be discussed further.
Chess Chess End-Game -- King+Rook (black) versus King+Pawn (white) on a7. 36 attributes for 3196 cases and 2 classifications. The pawn is one step away from queening and it is black's turn to move. It is assumed that white cannot win if the pawn is queened.
TicTac Tic-Tac-Toe Endgame database. This database encodes the complete set of
possible
Toe board configurations at the end of tic-tac-toe games. 9
attributes for 958 cases and 2
classifications.
Garvan Thyroid function tests. A large set of data from patient tests relating to thyroid function tests. These case were run through the Garvan-ES1 expert system (Horn, et al. 1985) to provide consistent classifications. The goal of any new system would be to reproduce the same classification for the cases. 32 attributes for 21822 cases and 60 different classifications. These are part of a larger data set of 45000 cases covering 10 years. The cases chosen here are from a period when the data profiles did not appear to be changing over time and could be reasonably reordered randomly (Gaines & Compton 1994). The Garvan data in the Irvine data repository is a smaller subset of the same data. The Garvan data consist largely of real numbers representing laboratory results. Using the Garvan-ES1 pre-processor these were reduced to categories of high, low etc as used in the rules in the actual knowledge base. Both the preprocessed data and the raw data were used separately in the studies below.
Preparation
* collect a set of cases, and produce a knowledge base using a
machine learning mechanism - this becomes the basis for the Simulated Expert
(SE) (described more fully later). In these studies only the Induct/RDR
machine learning algorithm (Gaines 1991)was used as previous studies had shown
that this was equivalent to or better than other algorithms such as C4.5
(Quinlan 1992) (Compton, et al. 1995; Gaines & Compton 1992)
* Randomise the data to avoid 'lumpiness'. Four randomisations were
carried out and the graphs show the results of the four randomisations.
* Start with fresh RDR Expert System (ES), essentially an empty knowledge
base.
Processing
Step 1
* get the next case
Step 2
* ask the (simulated) expert for a conclusion
Step 3
* ask the ES under construction for a conclusion
Step 4
* if they agree, get another case and go back to Step 1
Step 5
* if the Expert and the ES disagree, make a new (valid) rule and go
back to 1.
Step 5 is the crux. The new rule needs to be constructed and located in the KB. For a RDR simulation, this step consists of:
Step 5
* Run the case against the ML generated KBS and produce a rule
trace. This is essentially
the justification for the conclusion.
* Run the case on the developing RDR ES and identify the last rule
satisfied and the last rule evaluated. The new rule will be attached to the
true or false branch of the last rule evaluated according to the evaluation.
That is, the new rule will be reached only if exactly the same conditions are
satisfied.
* Obtain the difference list based on the current case and the case
attached to the last true rule. This difference list provides a filter to
select valid conditions that can be used in a new rule.
* Using a combination of the expert's justification (the ML KBS rule trace;
i.e. the rules satisfied in reaching a conclusion) and the difference list to
create a new rule and attach it. The level of expertise of the simulated
expert can be varied here by the mix of conditions selected, but in this study
only a single expert was used.
Level of Expertise
* Choose all conditions from the intersection of the ML KBS rule
trace for the case and the difference list for the case. If there are no
conditions available in the intersection then a single condition is chosen from
the difference list. This very similar to the "smartest" expert used in the
previous studies (Compton, et al. 1995). In reality, it is somewhat
smarter than the "smartest" expert used in those studies.
Warnings
* Initially, we did not in fact use the warnings to prompt for
knowledge acquisition but corrected all errors as above. We simply recorded
warnings as they occurred. These studies were carried out for the domains of
Garvan, Chess and Tic Tac Toe. Warning criteria were accumulated and warnings
generated both with respect to the individual rule that gave the final
conclusion (equivalent to the rule pathway for RDR) and the individual
conclusions. That is, a case would generate a warning if it was the first case
to follow a particular rule pathway through the KBS which had some particular
value for an attribute. It would also generate a warning if it was the first
case to be given a particular conclusion that had some particular value for an
attribute. Normally there are a number of different rule paths that reach the
same conclusion.
The studies were repeated for the Garvan domain, but with the added restriction that rules would only be created when warnings were made.
Method #1 - Warnings NOT Influencing Rule Creation
IF warning
flag case as FALSE POSITIVE warning
update warning criteria so case not warned about
ELSIF if no warning
flag case as TRUE NEGATIVE
ELSIF conclusion incorrect
add new rule (see simulated expert above)
start warning criteria for new rule based on this case
IF warning
flag case as TRUE POSITIVE
ELSIF no warning
flag case as FALSE NEGATIVE
IF conclusion correct
Method #2 - Warnings Influencing Rule Creation
IF warning
flag case as FALSE POSITIVE warning
update warning criteria so case not warned about
ELSIF if no warning
flag case as TRUE NEGATIVE
ELSIF conclusion incorrect
IF warning
add new rule (see simulated expert above)
start warning criteria for new rule based on this case
flag case as TRUE POSITIVE
ELSIF no warning
flag case as FALSE NEGATIVE
IF conclusion correct
(cases where RDR made an error but no warning was given)

True Positives
(cases where RDR made an error and a warning was given)
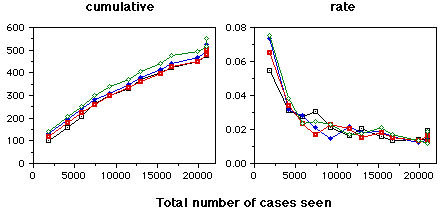
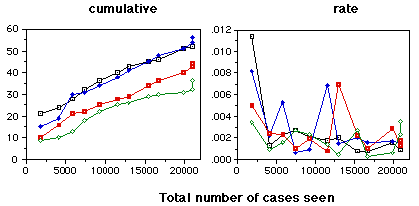
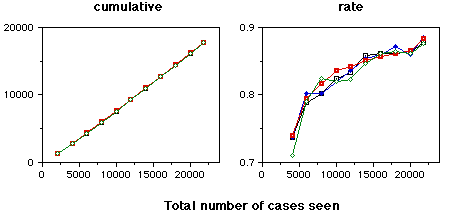
The graphs on this page are cases where the RDR system had made an error so that a new rule needed to be added. The top graphs indicates the cases where the warning system failed to issue a warning. The bottom graphs indicate those that were correctly warned about. The four lines on each graph are for four randomisations of the data. All errors were corrected as they occurred.
(cases where RDR was correct and no warning was given)
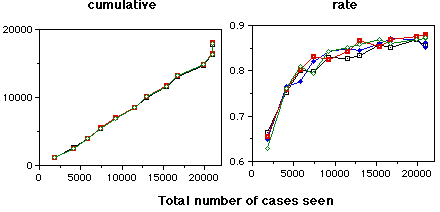
(cases where RDR was correct but a warning was given)
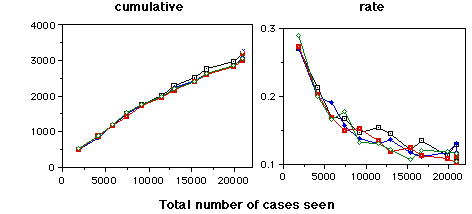
The graphs on this page are cases where the RDR system did not make an error - the case was correctly handled. The top graphs indicates the cases where the warning system correctly did not issue a warning. The bottom graphs indicate cases where warnings were generated unnecessarily. The four lines on each graph are for four randomisations of the data. All errors were corrected as they occurred.
(cases where RDR made an error but no warning was given)
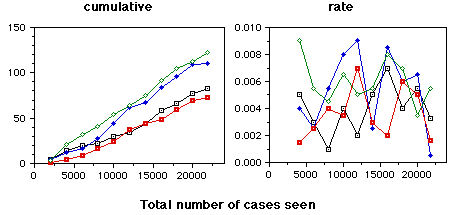
True Positives
(cases where RDR made an error and a warning was given)
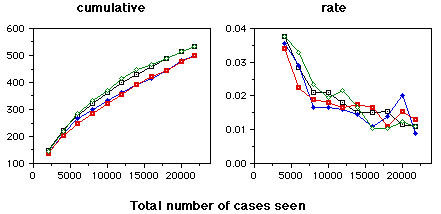
(cases where RDR was correct and no warning was given)
(cases where RDR was correct but a warning was given)
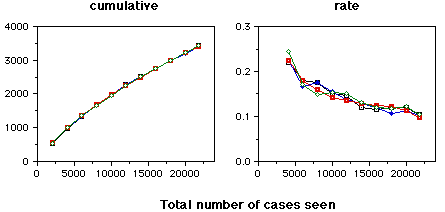
The graphs on this page are cases where the RDR system did not make an error - the case was correctly handled. The top graphs indicates the cases where the warning system correctly did not issue a warning. The bottom graphs indicate cases where warnings were generated unnecessarily. The four lines on each graph are for four randomisations of the data. All errors were corrected as they occurred.
False Negatives %
|
True
Positives %
|
True
Negatives %
|
False
Positives %
| |
| Garvan
rules 21822 cases
(all errors fixed)
|
0.2
|
2.4
|
83
|
15
|
| Garvan
rules 21822 cases
(only warned errors fixed)
|
0.4
|
2.4
|
82
|
15
|
| Garvan
concls 21822 cases
(all errors fixed)
|
1.4
|
1.3
|
90
|
8
|
| Chess
rules 3196 cases
(all errors fixed)
|
0.3
|
1.3
|
91
|
7
|
| Tic
Tac Toe rules 958 cases
(all errors fixed)
|
1.5
|
3.8
|
81
|
14
|
In the case of the Garvan data where warnings did not influence the creation of rules, the system correctly generated warnings for 92% of the cases that were misinterpreted during system development. That is, it failed to seek a second opinion in only 8% of the cases where it was necessary to seek a more expert opinion. This contrasts with the situation where the system was influenced by warning during rule construction.
In the situation where rules were added only when warnings were given (Garvan data), the system correctly generated warnings for 86% of the cases that were misinterpreted during system development. That is, it failed to seek a second opinion in only 14% of the cases where it was necessary to seek a more expert view. It is also worth noting that the total number of errors made, despite starting from an empty knowledge bases is only 2.8%, so that overall we talking about undetected errors of only 0.4%. This figure of 0.4% is a function of both the warning system and the low error rate of 2.8% which is a function of the RDR methodology which outperforms inductive methods, at least until very large numbers of cases are seen (Compton, et al. 1995). On the other hand it generated spurious warnings for some 15% of the cases seen.
Although the goal of a system that correctly warns about all errors has not been reached, these results seem extraordinarily good. In starting off with an empty knowledge base and asking the KBS to warn when any of its conclusions might be erroneous, only 0.4% of cases have undetected errors. If reliability is taken to mean not only accuracy, but knowing when the apparent conclusion might be unreliable, then this approach is far more reliable than many very highly engineered and well tested KBS. The overall accuracy of the system at 2.8% is comparable to many such systems, but if we are talking about undetected error the reliability of the system is 0.4%. We can note again that overall here means the entire development process from when the first rules are obtained from the expert until development is effectively complete.
In terms of facilitating knowledge acquisition, a conventional RDR development requires all output from the system to be checked until an appropriate level of performance for the domain is reached. Here only 17-18% of cases are required to be checked to achieve a reliability (no errors permitted) of 99.8%.
The results for the other domains are not as good for reasons that will be discussed. Firstly, it should be noted that all the other data is taken from studies where all errors were fixed and so should be compared to the Garvan results for the same protocol. That is where only 8% of the Garvan errors were undetected. In the Chess domain 19% of the errors were missed, but this still represents undetected errors in only 0.3% of cases seen. The unnecessary warning rate however was lower at 7%. The Tic Tac Toe domain was poorer with 28% of the errors missed which was in fact 1.5% of the total cases seen. The unnecessary warnings were 14%.
Finally the worst case of all was for warnings generated for conclusions rather than rules. Here for the Garvan data 52% of the errors were missed. That is there were undetected errors in 1.4% of cases seen. We also carried out studies on conclusion based warnings for Tic Tac Toe and Chess with a similar degradation in performance. We also collected data for these domains at a number of different stages of development as in the graphs for the Garvan domain, but the development profile is similar.
An immediate conclusion from this result is that it would not be particularly useful to use this approach for conventional KBS by keeping case profiles for conclusions. It is also unlikely there would be much advantage in keeping case profile for individual rules. As discussed earlier, in conventional systems and as in Clancey's specification of heuristic classification, rules may use conditions which are given as conclusions of other rules with the implication that a number of rules may make such conclusions, thus producing the same problem as with case profiles attached to conclusions. We have also noted earlier the requirement of ensuring that any maintenance does not effect rule pathways for previous cases.
We have examined by hand the 47 false negative cases from the Garvan domain (all errors corrected and rule based warnings) and nearly all of them relate to the situation where the results are almost normal. A single slightly abnormal result does not effect a conclusion of normal, but a number of these may result in a different conclusion. In fact there may be a number of slightly different conclusions depending on the particular profile. In this situation the range of values seen by the rule before a peculiar case comes along means that no individual attribute has an unusual value. Note that these false negative cases occurred even for the protocol where all errors were corrected and are due mainly to the limitation of the single attribute approach, (although better experts may also improve this result - see below). Half the false negatives in the protocol where corrections were only made when warnings were given were due to the failure to add a further rule rather than an intrinsic difficulty with the case.
It is worth noting that in manual studies reported previously, there were no false negative results (Edwards, et al. 1995). In this study a thyroid knowledge base similar to the Garvan domain was developed by the human expert, but the data was taken from a larger pathology service so that there were many more irrelevant attributes. We conclude that this is due to the superiority of the human expert over the simulated expert. The machine learning based rules on which the simulated expert is based are highly accurate as part of the overall ML KBS, but often such rules are not very intelligible or at least not very natural for an expert so that selecting part of such a rule trace as representing an expert is problematic. In these studies the false positive results were of the order of 40% because of the many attributes for other sub-domains not under consideration while building the thyroid system.
The weaker results with the Tic Tac Toe and Chess domains are, with hindsight, only to be expected and these were probably poor domains to use. It is in fact surprising that the results are as good as they are. The nine attributes of TicTac Toe represent the nine positions in the game with the values representing whether the position is occupied by an X or O. The value of any attribute is only relevant in terms of the values of the other attributes.
IF conclusion = hypothyroid and TSH_HIGH (exception)
THEN TSH_HIGH (not_exception)
This rule withdraws this particular exception. A warning is given if there are one or more exceptions after processing by the second knowledge base.
To be consistent this knowledge base itself needs an exceptions mechanism. However, it is interesting to note that this process does not need to continue recursively. With respect to the second knowledge base, an exception would not generate a different warning, but effectively it would simply re-instate the original exception so that a warning would be given. The second KBS would re-instate the warning if there was anything unusual about the case, where the case for the second knowledge base is the original case plus any first KBS exceptions. If the warning should not be given and the second KBS rule is confirmed, the attribute values allowed for the rule would simply be updated. If the warning should have been given then the first KBS is updated. We are not concerned with the case where the change in data is a new exception from the first KBS as this would have resulted in a warning regardless of the second KBS rule we are considering.
We have not tested this refinement yet. It is clear from expert comments that it would be simple to acquire rules to override exceptions, but we have no insight as to whether second level exception mechanisms would be useful in practice.
One obvious solution would be to provide a table for a pair of attributes, with a cell for each attribute value pair. As particular combinations of attribute value pairs occur the table would be filled in. If a pair of values for a so far empty cell occured a warning would be generated. Such tables could also be higher dimensionality and a table would be required for every possible combination of attributes. This idea is derived from the techniques used in rough sets (Pawlak 1991). The problem with this approach is in deciding on an appropriate dimensionality. One would imagine for pathology data that two dimensions would probably be enough. It should be noted that in PEIRS the average rule had one to two conditions indicating that the combination of conditions that indicated an alternate conclusion was small. For Tic Tac Toe a three dimensional table would be essential. Such tables would require some effort in maintenance and would be very likely to increase the false positive rate so that more effort would be required for the second knowledge base. Secondly, the method assumes attributes with a small number of discrete values. If real numbers were being considered one would probably have to include simple mathematical relationships such as ratios, differences or whatever relationships may reveal exceptions.
An easier alternative to manage would be to keep all the cases that satisfied each rule, or at least keep an example of each different data profile that satisfied each rule. Again this assumes attributes with discrete values. Any cases which did not fit into an existing pattern would raise a warning. Presumably, a missing value would be assumed to have any value and so not generate a warning. One would again imagine the false positive rate to be high. However, it may be possible that this would decrease to acceptable levels after some time, and again a second KBS could be used.
Clancey, W.J. (1985). Heuristic classification, Artificial Intelligence 27: 289-350.
Clancey, W.J. (1992). Model construction operators, Artificial Intelligence 53, 1-115.
Colomb, R. and Sienkiewicz, J. (1996). Analysis of Redundancy in Expert System Case Data in X Yao, AI'95 Eighth Australian Joint Conference on Artificial Intelligence, Singapore, World Scientific, 395-402.
Colomb, R.M. and Chung, C.Y. (1990). Very fast decision table execution of propositional expert systems in AAAI-90, Boston, MIT Press, 671-676.
Compton, P., Horn, R., Quinlan, R. and Lazarus, L. (1989). Maintaining an expert system in J R Quinlan, Applications of Expert Systems, London, Addison Wesley, 366-385.
Compton, P., Preston, P. and Kang, B. (1995). The Use of Simulated Experts in Evaluating Knowledge Acquisition in B Gaines & M Musen, Proceedings of the 9th AAAI-Sponsored Banff Knowledge Acquisition for Knowledge-Based Systems Workshop, Banff, Canada, University of Calgary, 12.1-12.18.
Compton, P., Preston, P., Kang, B. and Yip, T. (1994). Local patching produces compact knowledge bases in L Steels, G Schreiber & W Van de Velde, A Future for Knowledge Acqusition: Proceedings of EKAW'94, Berlin, Springer Verlag, 104-117.
Compton, P.J. and Jansen, R. (1990). A philosophical basis for knowledge acquisition, Knowledge Acquisition 2: 241-257.
Edwards, G., Compton, P., Malor, R., Srinivasan, A. and Lazarus, L. (1993). PEIRS: a pathologist maintained expert system for the interpretation of chemical pathology reports, Pathology 25: 27-34.
Edwards, G., Kang, B., Preston, P. and Compton, P. (1995). Prudent expert systems with credentials: Managing the expertise of decision support systems, Int. J. Biomed. Comput. 40: 125-132.
Gaines, B. (1991). Induction and visualisation of rules with exceptions in J Boose & B Gaines, 6th AAAI Knowledge Acquisition for Knowledge Based Systems Workshop, Bannf, 7.1-7.17.
Gaines, B. and Compton, P. (1994). Induction of Meta-Knowledge about Knowledge Discovery, IEEE Transactions on Knowledge and Data Engineering 5 (6): 990-992.
Gaines, B. and Shaw, M. (1990). Cognitive and Logical Foundations of Knowledge Acquisition in 5th AAAI Knowledge Acquisition for Knowledge Based Systems Workshop, Bannf, 9.1-9.25.
Gaines, B.R. and Compton, P.J. (1992). Induction of Ripple Down Rules in A Adams & L Sterling, AI '92. Proceedings of the 5th Australian Joint Conference on Artificial Intelligence, Hobart, Tasmania, World Scientific, Singapore, 349-354.
Horn, K., Compton, P.J., Lazarus, L. and Quinlan, J.R. (1985). An expert system for the interpretation of thyroid assays in a clinical laboratory, Aust Comput J 17 (1): 7-11.
Kang, B. (1996). Multiple Classification Ripple Down Rules. PhD thesis, University of New South Wales.
Kang, B. and Compton, P. (1992). Towards a process memory in J Boose, W Clancey, B Gaines & A Rappaport, AAAI Spring Symposium: Cognitive aspects of knowledge acquisition, Stanford University, 139-146.
Kang, B., Compton, P. and Preston, P. (1995). Multiple Classification Ripple Down Rules : Evaluation and Possibilities in B Gaines & M Musen, Proceedings of the 9th AAAI-Sponsored Banff Knowledge Acquisition for Knowledge-Based Systems Workshop, Banff, Canada, University of Calgary, 17.1-17.20.
Kang, B.H. and Compton, P. (1995). A Maintenance Approach to Case-Based Reasoning in J P Haton, K Keane & M Manago, Advances in Case-Based Reasoning, Berlin, Springer Verlag, 226-239.
Lenat, D. and Feigenbaum, E. (1991). On the thresholds of knowledge, Artificial Intelligence 47 (1-3): 185-250.
Pawlak, Z. (1991). Rough Sets: Theoretical Aspects of Reasoning about Data, Kluwer Academic Publishers, Dordrecht.
Preece, A.D., Shinghal, R. and Batarekh, A. (1992). Principles and practice in verifying rule-based systems, The Knowledge Engineering Review 7 (2): 115-141.
Quinlan, J. (1992). C4.5: Programs for Machine Learning, Morgan Kaufmann.
Zdrahal, Z. and Motta, E. (1994). An In-Depth Analysis of Propose and Revise Problem Solving Methods in R Mizoguchi, H Motoda, J Boose, B Gaines & P Compton, Proceedings of the Third Japanese Knowledge Acquisition for Knowledge-Based Systems Workshop (JKAW'94), Tokyo, Japanese Society for Artificial Intelligence, 89-106.