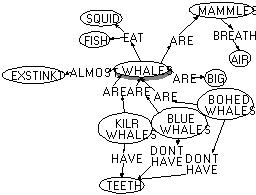
Figure 1: A concept map drawn by a first grade student.
Concept maps are used in a wide variety of disciplines because of their ability to make complex information structures explicit. The Web is an excellent medium in which to make concept maps available for real-time, multi-user interaction for planning, decision making, documenting, and designing tasks, or merely as a navigational aid to information. KSIMapper is a program that can run as a Netscape plug-in to allow this kind of flexible interaction.
Concept maps can be used informally or formally - where the graphical "syntax" of the maps is tightly controlled. Both forms are needed. Graphs is a program in which users can constrain arbitrary graphs to conform to any of a wide variety of graphical formalisms. The Graphs program is combined with KSIMapper to bring it a graphical user interface: the two can function as a multi-user, interactive concept mapping system on the Web, and together can transcend informal concept mapping and at least several concept mapping formalisms.
Concept mapping is a simple and intuitive visual form of knowledge representation. For human users, concept maps tend to make the structure of a body of knowledge much more salient than other forms of knowledge representation such as pure text and predicate logic (Nosek and Roth, 1990). Concept maps have been used in education (Novak and Gowin, 1984; Lambiotte, Dansereau, Cross, and Reynolds, 1984), in management (Axelrod, 1976; Eden, Jones and Sims, 1979; Banathy, 1991; Hart, 1977), in artificial intelligence (Quillian, 1968), in knowledge acquisition (McNeese, Zaff, Peio, Snyder, Duncan, and McFarren, 1990), in linguistics (Graesser and Clark, 1985; Sowa, 1984) and for many other varied purposes. Concept maps can (and have) been used to represent knowledge at the very informal level, such as for "brainstorming", as well as at the very formal level, such as executable expert systems (Gaines, 1991) or graphic forms (Eklund and Levinson, 1993; Ellis and Levinson, 1992) of Conceptual Graphs (Sowa, 1984) (see also Kremer (1994; 1995)).
Concept maps are graphs consisting of nodes with connecting arcs, which represent relationships between nodes (Lambiotte, Dansereau, Cross, and Reynolds, 1984). The nodes are labeled with descriptive text, representing the "concept", and the arcs are often labeled with a relationship type. Nodes may be represented using distinct visual attributes, such as shape and color, to distinguish node types; arcs may be similarly distinguished.
Figure 1 shows a concept map about whales by a first grade student. The arcs on the map are labeled with the relationship they represent: "EAT", "HAVE" and "ARE". The student was originally taught to do concept maps on paper without labelled arcs. He enthusiastically adapted to the software version and became quite at ease with labeled arcs after only minimal instruction.

Figure 1: A concept map drawn by a first grade student.
Individual authors can compose concept maps to conveniently convey non-linear information structures, but groups of authors may also benefit from this flexible form of knowledge representation. Of course, software designed for groups, rather than for individuals, requires special attention (Grudin, 1989; Cockbrun and Thimbleby, 1991). Besides the obvious need for the information to be placed in a repository conveniently accessible to all participants, various issues arise concerning participant awareness, security, data integrity, and role assignment. This paper will address one approach to the problem of designing software for use by groups: Concept maps are cast as interactive multimedia objects on the Web which can be embedded within HTML documents. Furthermore, the Web's usual distinct roles of authorship and readership are merged to produce a model of participantship which allows continuous incremental authoring of concept maps within Web documents - which have been traditionally regarded as fairly static. All of this may seem a bit abstract; so, Section 4 presents several applications which exemplify this style of concept map use on the Web.
The aforementioned discussion deals with the superficial aspects of concept maps: how to browse them, draw them, and share them; as well as what can be done with them. However, this ignores the important question of how to construct a system that can assume the unstructured character of informal concept maps (as in Figure 1), or impose the constraints that go along with a selection of diverse mapping formalisms such as Conceptual Graphs (Sowa, 1984), KRS (Gaines, 1991) (Classic (Borgida, Brachman, McGuiness, and Resnick, 1989)), or Petri nets (Reisig, 1985). The author's current work on this subject is discussed in Section 5.
There can be little doubt that World Wide Web (WWW) browsers have caught on as a popular means of accessing information on the internet with unprecedented success. It makes good sense to take advantage of their success, whatever the cause one attributes to it, and use the Web as the base infrastructure for a repository of concept maps. Indeed, concept mapping tools should be cleanly integrated with all the other objects normally found on the Web: text, rich text, still images, animation, and HTML forms, to name just a few of the wide variety of multimedia objects that have become widely available on the Web.
The current versions of the Netscape WWW browser allows concept mapping programs, written in C++, to be cleanly integrated with the browser such that users can interact with the concept map as easily as they might interact with a clickable image. Concept maps can be used just as though they were native objects to the browser program. Figure 2 shows a Smart Ideas concept map embedded in an HTML document. This document and concept map describe part of a C++ class library. The concept map is actually a local hypertext of maps which can be navigated within its picture frame. The status bar just below the map contains the map's name within the local (within frame) hypertext, as well as a local "back" button for local hypertext navigation. The concept map itself can be re-arranged by simple direct manipulation commands. Nodes and arcs in the map carry visual attributes to indicate their type. Drop-down shadows on nodes indicate that the node may be clicked to navigate either to another local map (within the current document), or to a different Web document.
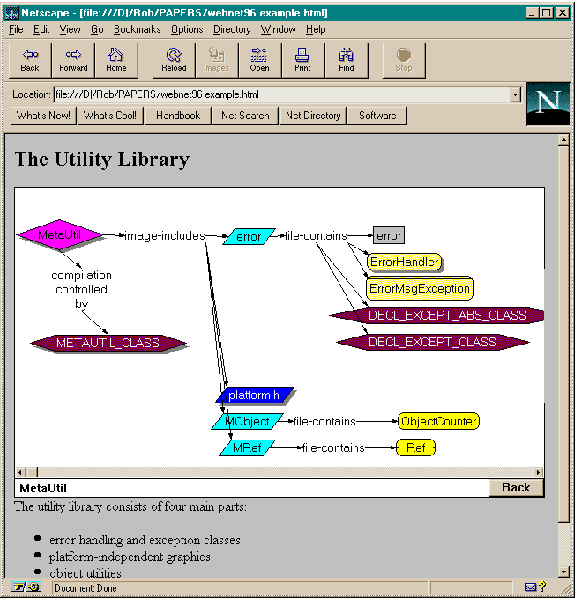
Figure 2: A concept map embedded in an HTML document describing part of a C++ class library.
All this is possible through the plugin Application Program Interface (API) provided by Netscape. Plugins are programs which register themselves with the Netscape browser in association with a specific MIME type (Borenstein and Freed, 1993), and are dynamically loaded by Netscape whenever an object of that MIME type is displayed. Plugins can be either embedded in an HTML document or displayed as a complete document themselves.
With the version 3.0 release of the Netscape browser, plugins can masquerade as a Java (Sun, 1996) class. This facility is call LiveConnect (Netscape, 1996a). Java is an object-oriented programming language tailored for program migration on the Web, and is fast becoming the "native" Web language. In presenting itself as a Java class, a plugin program can make public any internal commands the programmer deems appropriate. Thus, a Java program can assume full control of a plugin program and provide specialized interfaces and operations to a concept map in a way that is convenient for Web programmers.
Furthermore, LiveConnect also provides open communication between Java and JavaScript (Netscape, 1996b). JavaScript is a scripting language that can be written directly into HTML documents, and is even easier to work with than Java. Since concept maps can masquerade as a Java class, and JavaScript can talk to Java, then JavaScript can exert control over concept maps. This allows the user input elements of Web documents (primarily HTML forms (Grobe, 1995)) to act as a large part of the interface to concept maps, giving the end user (or HTML script writer) an unprecedented degree of flexibility and ease of control.
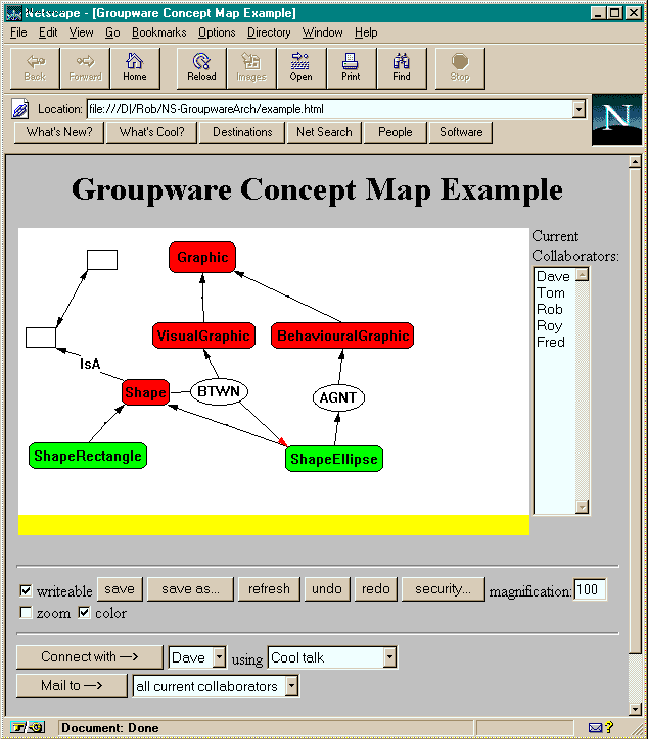
Figure 3: A concept map embedded in a HTML document using HTML forms input elements and JavaScript to achieve a custom user interface.
Figure 3 shows a KSIMapper concept map embedded in an HTML document. In this example, most of the non-direct manipulation user interface elements that would normally appear as menus or hot keys have been transformed into commands available through a Java class. HTML forms input elements, such as buttons and selection boxes, are scripted with JavaScript to access these commands. For example, the button in Figure 3 labeled "save" is simply defined as:
<input type="button" name="save" value="save" onClick="document.map.save()">
which will call the save() method of the plug-in applet.
While concept maps can be very useful as Web documents, their usefulness can be dramatically increased by making them multi-user interactive documents. That is, the traditional distinctions between document author and reader can be dissolved to create a participant role, where (sufficiently privileged) individuals can not only browse a concept map but also change the document and store the modified document back to the server. Furthermore, if two or more users happen to access a particular document at the same time, they should be able to smoothly move into a synchronous shared editing session.
Allowing users to update concept maps from a Web browser is accomplished through use of the CGI (Common Gateway Interface), available on most WWW servers. A shared concept map is not directly referenced by its normal URL; instead, a custom CGI program is referenced, and this reference is parameterized with a reference to the actual concept map document. When the URL is fetched by the client browser, it is the responsibility of the CGI program to return the concept map data on behalf of the server.
When the client wishes to save the concept map, the same indirect URL is used, but with the concept map data as part of the post message. The CGI program is called by the server, and the CGI program copies the data back into the original file on the server.
Of course, this simplistic approach is open to malicious or accidental disruption of the data. A host of security issues come to mind. While these issues have not been addressed so far in this research, there are many well-tested solutions elsewhere. Version control, which can be as simple as maintaining a new version of a file every time it is written back to the server, is one approach; public-key encrypted electronic signatures being verified on a write-back is another.
Merely allowing users to write concept maps back to the server is not enough. Besides the obvious dangers of users overwriting each others work, users need to be kept aware of other users concurrently accessing the concept map. Users may also wish to find out more about various aspects of the history of the map, such as who else has modified it.
Since shared concept map access is through a server CGI program, this program can take responsibility for recording access as part of the concept map's history, and for coordinating "real time" interaction between concurrent participants. Thus, clients can obtain information about past and current participants from the server (as in Figure 3). Furthermore, since the software architecture uses command objects (Gamma, Helm, Johnson, and Vlissides, 1995) to encapsulate all user updates to a concept map's state, these command objects can be sent to the server where they can be re-broadcast to all concurrent participants. In this way, each of the participants will receive all participants' commands, and all particpants' concept maps will eventually arrive at the same state. (There are many finer points to this kind of interaction, but they will not be discussed here.)
This form of interaction has the advantage of being serendipitous; that is, users need not go to any special trouble to set up a "conference"; instead interactive sessions are automatically set up by virtue of concurrent access to the same concept map. (See (Roseman and Greenberg, 1996) for a discussion of this kind of interaction.)
As already mentioned in the introduction, concept maps are used in a variety of diverse fields. This section describes several applications where Web-based concept mapping tools, in particular, can be used.
If one ignores the groupware possibilities and follows a more traditional author/reader model of Web authoring, concept maps can play a role on the Web very similar to that of clickable images. An author designs and constructs a concept map off-line, then posts the finished product on the Web; readers do not have any ability to modify the artifact. Figure 2 is an example of this sort of "read-only" Web concept map. Although readers cannot change the map permanently, they can perform certain actions, as prescribed by the author, such as clicking on a node to navigate to other information.
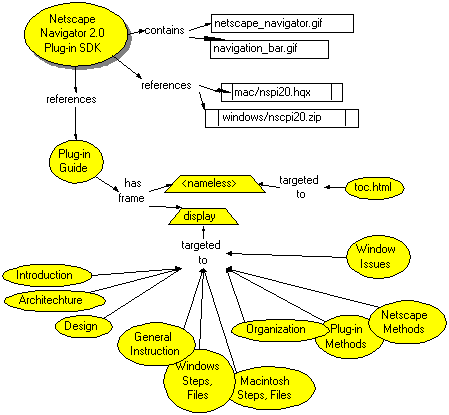
Figure 4: A two-level breakdown of the documents navigable from the Plug-in SDK page on Netscape's Web site.
In the case of Smart Ideas concept maps, which encapsulate a local hypertext of concept maps, the author has a choice of a node either being a hyperlink to another Web document or being a local hyperlink within the local hypertext of concept maps. In the later case, the Web document remains displayed; only the sub-window in which the concept map is displayed gets replaced by the new map. A local "back" button helps to maintain the users' context by providing the ability to backtrack.
Typically, well-written Web document collections use lists of links as a "tables or contents" to aid readers as they navigate through the material (Tilton, 1996). Concept maps can be used to the same end. Rather than a simple table of contents list, the reader can be presented with a concept map describing the document collection. The reader can then click on the concept map nodes to navigate the site. In this scenario, the nodes represent possible destinations in the information space, and arcs represent the relationships between them. Concept maps have an advantage over simple (or even hierarchical) lists in several areas:
Concept maps suffer from their tendency to take up more precious screen real estate than lists, but often this can be mitigated by scrolling and nesting maps.
Concept maps, used as a information navigational aid, can be used to make explicit the structure of a publicly accessible Web site on the internet (for example, see Figure 4). In much the same way, concept maps can be used privately on an "intranet" to function as a guide to a corporation's internal information bank, or, more extensively, as a "corporate memory".
In general, (especially with corporate sites) WWW sites tend to be relatively finished and polished before they are released. Yet if the social situation is appropriate, less polished material, or early draft versions of material may be posted on a site as well. These untidy documents can be properly indexed and left as an easy-to-access "corporate memory", which can be used to trace the history of an organization's activities. The advantage of such an approach is that it is easy to create (if most work is done on the Web site anyway), easy to maintain, easy to access, and inherently a good match with the very loosely structured historical data.
Concept maps are good tools for brainstorming sessions. The author has used concept maps with considerable success in brainstorming meetings (Kremer, 1993) - the nodes and arcs act as concrete symbols for ideas, and the arcs allow one to draw complex relationships among them, arranging, comparing, contrasting, and grouping ideas. Concept maps can be used for brainstorming by individuals or groups for everything from corporate decision making, to design, to organizing papers, to formulating research plans. Figure 5 is an example of a concept map developed during a group brainstorming session.
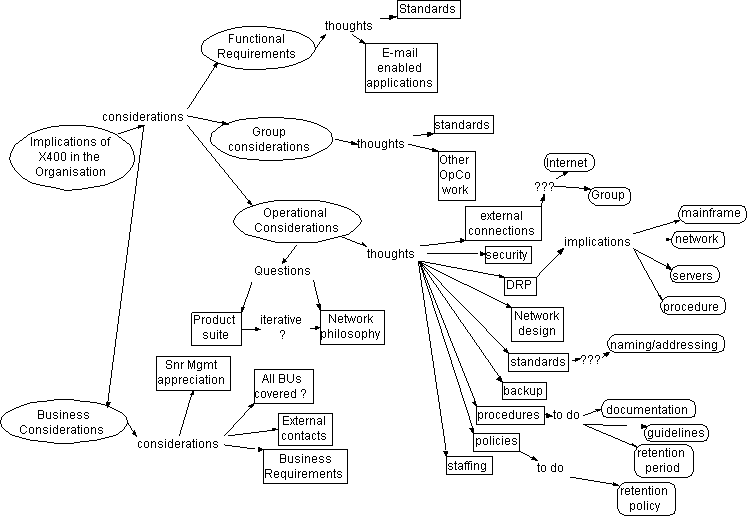
Figure 5: A concept map developed by a three member group brainstorming network design (Kremer, 1993).
Because brainstorming tools demand very quick and easy entry of ideas, even if they seem vague or unrelated, concept maps for brainstorming should be untyped or, if they are typed, it should be very easy to override the constraints of the type system. An example of a typed concept map system that can be used for brainstorming is gIBIS (Conklin and Begeman 1987) which has only three node types and seven arc types. Figure 6 shows the legal node and arc types of a gIBIS concept map.
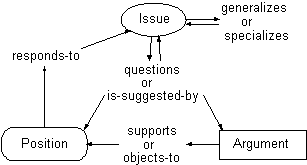
Figure 6: The legal nodes and arc types in the gIBIS decision-support model. Arcs are constrained to connect only the nodes that they connect in the diagram.
In contrast to brainstorming techniques, there is a diverse class of tasks which demands a much higher degree of structure. For lack of a better term, one may refer to them as disciplined modeling tasks. What these tasks have in common is a need to be constrained by a specific formal or semiformal model. Examples of such tasks include:
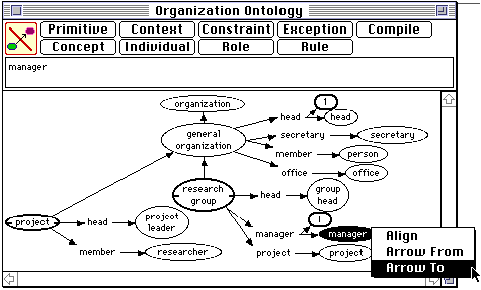
Figure 7: A simple KDraw concept map which is part of an expert system (Gaines, 1993).
Disciplined modeling is by nature more formal than either of the other two application areas, and users of these systems expect to work harder to achieve their goals. However, one must keep in mind that the artifacts of these more formal works do not generally spring up in one flash of divine inspiration; but rather, the architects of such works work long and hard at designing, redesigning, recasting, refining, expanding, condensing, and tweaking the product to achieve a consistent artifact that conforms to the constraints of the chosen formalism. During this process the data can become temporarily inconsistent and violate the formalism's constraints. Indeed, near the beginning of the process, the developers may not even have decided which formalism their product will eventually conform to. It becomes obvious that even very formal systems must support some degree of flexibility. Furthermore, a single system may have to support informality, and several choices of formalisms. (See Kremer (1994; 1995) for more detailed discussion.)
For example, knowledge engineers faced with the task of creating an expert system about widgets may know little about widgets at the start of their task. They cannot expect to understand which formalism will eventually be appropriate. They may have to work with several experts and other sources. They must immediately start making extensive notes about vocabulary, terms, concepts, and relationships at their first expert interview. It will not be until after several knowledge acquisition sessions that they can hope to arrive at a decision about the structure of the knowledge. Once they have decided on the structure, they can pick the appropriate formalism: but it would be a lot of work to transfer all their notes from their note-taking system to a new system. If only their note-taking system could "adapt" to the new formalism!
To address this problem, the author's current research is directed at constructing a very flexible and generic concept mapping package that may be attached to a constraint graph which can be annotated with rules to implement a wide variety of graphical formalisms.
The purpose of a constraint graph is to provide an abstract mechanism to describe a graphical formalism. Constraint graphs are formally specified using a dialect of the specification language Z (Hayes, 1987) called ZSL (Jia, 1995). The complete specification is posted on the Web at http://www.cpsc.ucalgary.ca/~kremer/graphs/GraphsZ.htm (Kremer, 1996a). The basic premise is that all graphs contain only three basic object types: nodes, arcs, and contexts (collectively referred to as components). Each of the basic types may be further elaborated into a lattice of subtypes. Each new subtype can introduce new attributes on top of those of its parent type. Predicates are attached to each subtype and are used to constrain the graph to conform to a particular formalism.
Interestingly, the traditional distinction between a type and an object is abandoned. But one may consider a component to be an object if it possesses a "~xx<this" predicate ("there is nothing that is a proper subtype of me"). Actually, the predicate "x|x<this~yy<x" ("nothing that is a proper subtype of me has any proper subtypes") is more common. For example, for the Classic formalism, such a predicate is used to describe the fact the no Individual can be a superclass (but the Individual object itself has to have subclasses, or there would be no individuals!).
The type lattice of a constraint graph is fully integrated with the graph itself. That is, is-a arcs are just a subtype of the basic arc and are "drawn" into the graph just as any ordinary arc type (like owns, has-color, or bigger-than) would be. Of course, is-a adds several constraints on top of a basic arc because the is-a projection of the graph must be a lattice. These constrains include the fact that is-a arcs cannot form cycles and is-a arcs are always directed binary arcs. The type system is so well integrated with the graph system that users may specify the type of an object by drawing an is-a arc from the object to its type object (or by selecting its type from a menu at create time).
The addition of an is-a arc to a graph causes the system do a type check. This involves evaluating the predicates. A predicate takes as parameters the graph itself, the target object (the one in question), and the object that the predicate is actually attached to. A new is-a arc is legal if and only if
A object is legal if and only if
In addition, an arc is legal if and only if
Since an is-a is itself a kind of arc, all of these constraints apply to is-a and its subtypes.
A common concern is constraining the types in which arcs can terminate. This is accomplished by simply attaching the terminals of the defining arc to the appropriate type objects. More complex cases can be handled using predicates. For example, the brother relationship can be constrained (without bothering with a male-person concept) by the predicate
("brother is a binary relation between two persons where the second one is male"). Note that the second and third conjunct are redundant if
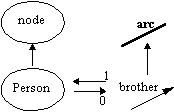
is drawn as the definition (by the second arc rule). Also note that the first conjunct, "this.arity=2" is still required to prevent a subtype of brother from becoming a trinary arc.
For convenience, a constraint graph is divided into levels. Level 1 consists of the graph types themselves -- node, arc, is-a and composite - and is immutable as far as the user is concerned. The designation of the rest of the levels is left to the discretion of the formalism implementor. Generally, levels 2 and 3 should be at the system level where the basic types are defined according to the target formalism. These types should normally be considered immutable by any end users, since to disrupt them may impede interpretation of the graph. Two system levels are often used (where level 2 is hidden from the end user and used for hidden type hierarchies, while level 3 is public and used to populate the space of type identifiers for the end user). Level 4 is generally considered to be the user level, where the end user builds some specific knowledge structure. More levels are possible: for example, level 4 might be used to construct types in some specific domain, and a fifth level might be added to hold objects of that domain within some hypothetical world.
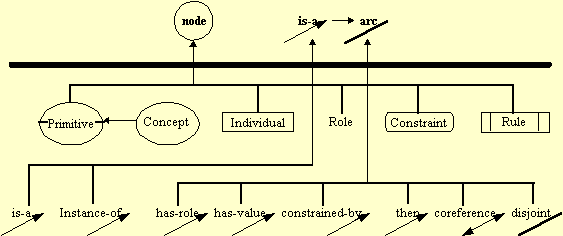
Figure 9: A constraint graph model of KDraw. The vertical and horizontal arcs represent the subtype relation. Objects above to heavy line the types of the contraint graph domain; objects below the heavy line are in system types in the KDraw domain.
As a more extended example, Figure 9 shows how a constraint graph can model KDraw (Gaines, 1991), a visual form of Classic (formally specified in Z in Kremer (1996b)). Figure 10 shows a Constraint Graphs schema for the object types in KDraw. Node labels all begin with upper-case letters; arcs (relationships) are pictured as all lower-case letters. The surrounds of nodes are the same shape and style used in KDraw. Arcs in KDraw are all unlabeled (they are only labeled here for clarity), and for most part, are binary directed arcs (arrows) unambiguously distinguished by the (visual) type of their terminal objects. The cases where arcs types are not unambiguous are those in which the arc types have both terminals at concepts: Is-a, exclusive, and coreferent. These are visually disambiguated by Is-a being a directed arc, exclusive being an undirected arc, and coreferent being a double-directed arc.
Above the heavy line in Figure 9 are the primitive (level 1) objects of the constraint graph: node, arc, and is-a. Is-a is a subtype of arc (and forms the type lattice of a constraint graph).
All the subtypes pictured below the heavy line in Figure 9 are not primitive in the constraint graph, but are added by a user describing KDraw. In the actual case used in the accompanying demonstration, these all belong to level 3. The basic node types are concept, primitive, individual, constraint, and rule. KDraw has nine relations, two of which are subtypes of the is-a arc. The is considerable semantics (rules) associated with the is-a arc (is-a arcs cannot form cycles, is-a arcs are binary, etc.) are automatically inherited by the subtype is-a and instance-of arcs.
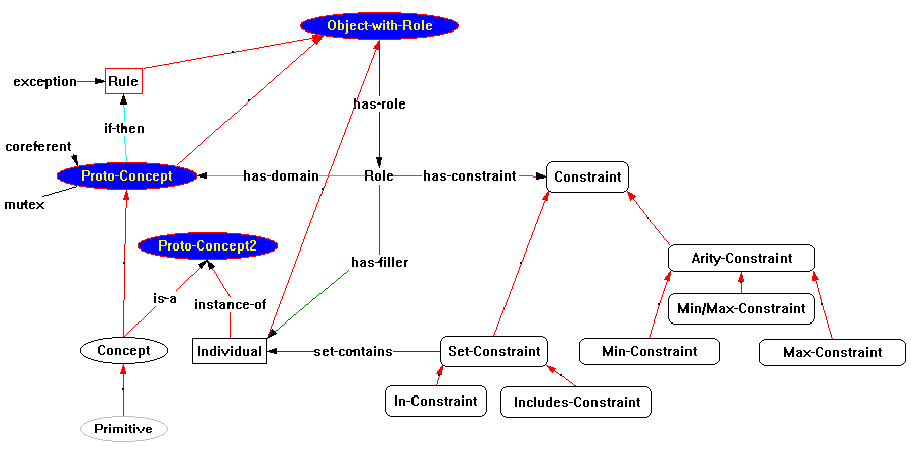
Figure 10: A Constraint Graphs schema of the object types in KDraw. Here, node labels all start with upper-case letters, legal arcs (relationships) are pictured in lower-case terms. No arc is legal unless the types of its terminals are subtypes of the terminal types in the diagram. The red unlabeled arcs are isa arcs. The dark shaded nodes (as well as Constraint, Arity-Constraint, and Set-Constraint) are hidden from the end user and are used to define the type hierarchy. The surrounds of nodes are similar shapes and styles to those used in KDraw.
Of course, each of the objects shown in Figure 9 must be constrained to conform to the graphical syntax of KDraw. This is done in the Constraint Graph schema of Figure 10. For nodes, this is trivial, for the arcs alone suffice to control the syntax. (Any nodes could stand alone and unattached without violating any rules, but they wouldn't be very meaningful.) For the most part, arcs can be constrained by merely connecting their terminals to the appropriate type object (as per the second link rule above). These terminals are (almost) precisely those shown in Figure 10. Complications arise due to the need to introduce additional types to encapsulate "polymorphic" relationships (such as has-role), and to handle the natural inheritance of visual attributes from Concepts to Individuals through instance-of arcs without giving Individuals all the semantics of Concepts (to be detailed below).
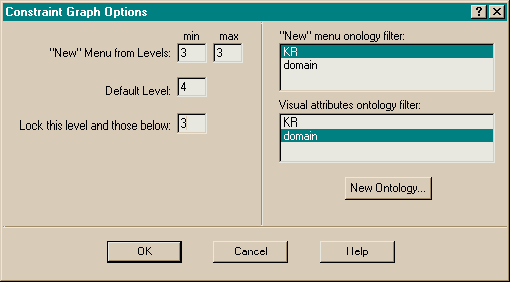
Figure 10 contains several nodes which are hidden from the user: Object-withRole, ProtoConcept, Constraint, Set-Constraint, and Arity-Constraint. These are hidden by placing them in level 2, and blocking level 2 from end user visibility using the options dialog (Figure 11). The purpose of these nodes is to allow "polymorphic" relationships between nodes. For example, there are four node types that can be the root of a has-role arc - Concept, Primitive, Rule, and Individual. This similarity is captured by introducing the (hidden) common supertype Object-with-Role. Similarly, the commonality among the various constraint types is captured by hidden common supertypes.
There are several other constraints necessary to emulate KDraw. These are added as predicates:
These links and rules are sufficient to constrain a graph to the legal graphical syntax of a KDraw. (It's still possible to construct a nonsensical graph, but that's another story!)
The distinctive shapes of the node surrounds in KDraw are modeled by attributes in the constraint graph system. The nodes in the KDraw domain are each given a shape attribute: for example, concept has "shape=ellipse", role has "shape=none". Attributes are inherited by subtypes; so, all subtypes of concept will have the "shape=ellipse" attribute. But things are not that simple, as the example in Figure 12 shows. In this example, we need to say not only that George is an instance-of Person, but also that George is-a individual. Clearly George is (and should be) both a subtype of the concept Person and of Individual. The semantics of KDraw dictates that the surround for George should be a rectangle and not an ellipse. But George inherits both "shape=rectangle" (from individual) and "shape=ellipse" (from person). How are these properly disambiguated? One may consider disambiguating using the predicates, but this would only allow or disallow a particular configuration; what is needed a way to automatically and efficiently choose the correct shape. The system used in Constraint Graphs is to extend attributes with properties. One of those properties is priority, which is of type natural number, {0, 1, 2, …}. The highest priority is 0. Using this scheme, individual's shape attribute is given the priority 0, and concept's shape attribute is given the priority 1. Thus, the system is able to efficiently compute George's shape as rectangle.
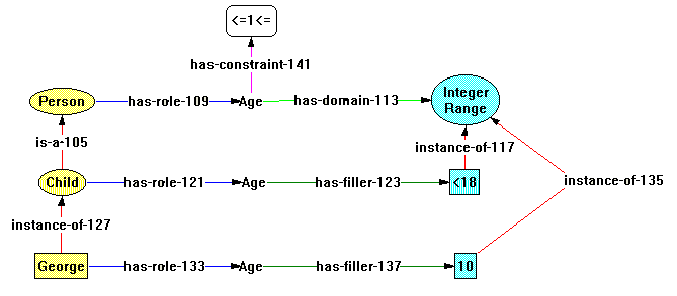
Figure 12: A simple KDraw example
A related problem is that George should naturally inherit the color that the user has given to Person, since George is an instance-of Person. Instance-of is a subtype of isa, so the color inheritance happens naturally. But Individuals must not inherit other abilities that a Concept supertype might have, such as the ability to be on the root side of a has-rule relationship (see Figure 10). This trick is accomplished by filtering appropriate isa arcs. The arc instance-of-127 is tagged (by a predicate rule in instance-of) with the domain filter (used by the visual inheritance system), while the graph is using the (mutually exclusive) KR filter to determine arc eligibility (see Figure 11).
Another problem arises because the visual syntax of KDraw is completely dictated by the surround shape; that is, users expect ellipses to represent concepts, rectangles to represent individuals, etc. If a user were to override the shape of concept, for instance, the concept map would be rendered unreadable (but still computable, because the system uses abstract types, not shape). On the other hand users could override other attributes, such as color, without effecting the readability of the map. This problem is solved by again using properties of attributes. A second property, constant, is introduced. A constant attribute cannot be overridden by any object at a lower level. Thus, the shape attribute can be locked on all KDraw objects, preventing users from changing the shape, while still allowing them to change attributes like color. Locking could easily be accomplished by using predicates, but since it occurs relatively often it is a part of the attribute system, where it is more convenient to specify.
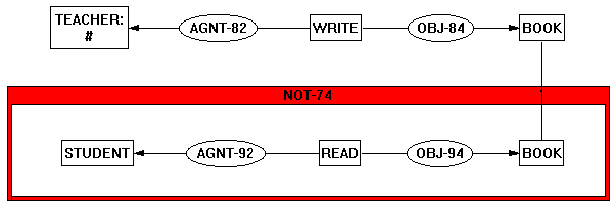
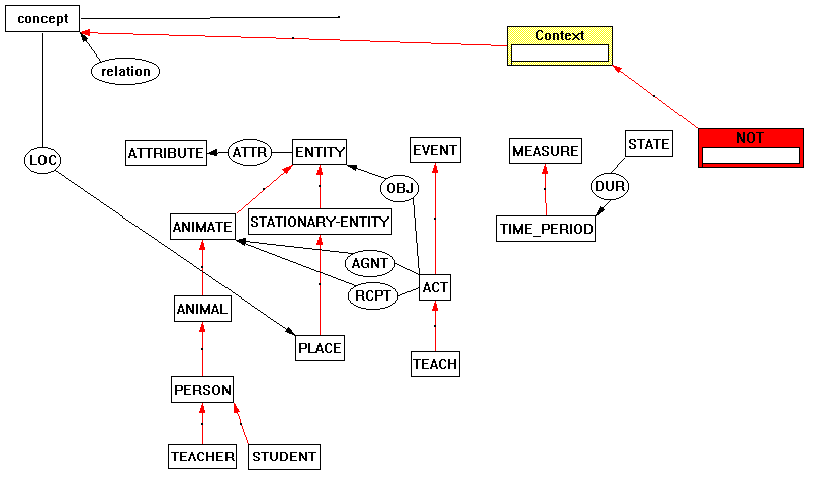
Figure 13 shows an example of a Conceptual Graph as represented by the Constraint Graphs program. The graph expresses the sentence "No student read the book the teacher wrote." The ontology used is shown in Figure 14. The user who constructed Figure 13 added the new types WRITE<ACT, READ<ACT, and BOOK<ENTITY. The ontology of Figure 14 is very straight forward. The level 3 system types include concept<node, relation<arc, coreferent<arc (unlabeled, at top center), and Context<context. The display of the relation and coreferent arcs is rather awkward and uninformative because KSIMapper currently has no good way of showing an arc with multiple terminals attached to the same object. To avoid clutter, the type hierarchy omits the isa arc between concept and relation and their immediate subtypes.
Conceptual Graphs assumes the graph is accompanied by a separate semantic net that specifies the type lattice. Constraint Graphs smoothly integrates these two separate graph structures into a single graphing space, so a Constraint Graphs implementation of Conceptual Graphs might be considered an extension of Conceptual Graphs.
The Constraint Graphs program is capable of informing the user of all legal links between arbitrary nodes. A little experimentation with this feature quickly points out a few problems with this ontology which appears in the appendix of Sowa's 1984 book (Sowa, 1984). For example, Sowa defines the LOC relation as [T]->(LOC)->[PLACE]as it is in Figure 14 (T is concept in the figure). This allows a user to draw an arc from a node of type TIME_PERIOD to a node of type PLACE: the system will automatically type it as either coreferent or LOC. Clearly, neither of these possibilities is appropriate since a TIME_PERIOD should not have a location, and it should be impossible for a TIME_PERIOD and a PLACE to be the same object. In the former case, it might make sense to introduce a common supertype for ENTITY and EVENT to anchor the LOC relationship instead of at T (concept).
The Constraint Graph program is capable of capturing the syntax of other graphical formalisms by inferencing via the type lattice, but the reader should be careful to note that it is not intended to take on the deeper semantic nuances of any arbitrary graphical formalism. For example, although it can emulate the syntax of KDraw, Constraint Graph cannot do the inferences of KDraw.
However, the Constraint Graph program is relatively easy to extend to "compile" a graph into the native notation of a target formalism. For example, it took only a single day to write an extension to output the graph as a complete Z specification - this automatic generation produced the specifications found in Kremer (1996b) and Kremer (1996c). Future work on this project includes adding an extension to compile a graph into KDraw's native notation, calling up a separate KDraw interpreter (possible elsewhere on the Web), and writing back the inferences into the original graph.
The reader might be confused at this point as to how the very concrete graphical tool on the Web is related to the rather abstract constraint graphs. In fact, both exist as separate programs: the graphical tool, KSIMapper, runs standalone or as a Netscape plug-in for drawing unconstrained concept maps; the constraint graphs program, Constraint Graphs, can be run standalone with a (not-very-intuitive) text-based interface. But the two programs are designed to be combined.
The combined programs' graphical interface is provided by KSIMapper. Each time a user creates a new object in the interface, a corresponding object is created in the constraint graph. The object in the constraint graph is checked for legality. If it is not legal, the creation is undone in both places and an appropriate message dispatched to the user. Likewise, for any modification to an object in the interface (such as changing the value of an attribute) the corresponding change is made in the constraint graph, checked for legality, and undone if it is not legal. Thus, the graphical interface is always kept in conformance to legal syntax according to the constraint graph.
Changes in one place in the graph may have affect changes in other places in the graph. For example, if the person concept has the attribute "color=green", and a user changed the attribute to "color=blue", then (assuming no subtype overrides the attribute value) all subtypes of person (primitive-concepts, concepts, or individuals) should also change their color to blue. This is accomplished easily in the program because when an KSIMapper object/Graphs object pair is created the two are linked using the observer pattern (Gamma, Helm, Johnson, and Vlissides, 1995) so that any changes to the Graphs object are broadcast to the corresponding KSIMapper object. When any attribute of a Graphs object changes, the changes are automatically propagated to all subtypes which, in turn, broadcast the update to all their observers in KSIMapper.
Since the two parts of the program, KSIMapper and Graphs, have such a high degree of independence, it should be relatively easy to reconfigure the software. For example, one could start with a very informal map drawn with KSIMapper alone (which imposes no constraints), and then "clip-on" a KDraw constraint graph to allow the gradual "formalization" of the map to match KDraw syntax. Work in this area has not yet been undertaken, but it looks relatively straight-forward. A more difficult problem is the smooth transition from one formalism to another (related) one. There are many more problems here, having to do with phasing out of one formalism and the introduction of another without producing too much inconsistency in the mean time.
Efficiency is also a significant problem in the current version of the software. The independence of the two halves of the program is paid for by a certain amount of redundancy, both in terms of space and time complexity. The checking of the legality of a object in a constraint graph also has a polynomial time complexity on the number of objects in the graph according the the specification. Actually, one of the implementations of the specification caches relationships, and so the time complexity is reduced to polynomical on the depth of the graph. However, there is lots of room for improvement here.
Constraint graphs have only been applied to KDraw and Conceptual Graphs to date. Applying them to other graphical formalisms such as Petri nets would be useful to show the utility of constraint graphs. This may also serve to further generalize the tool.
KSIMapper is fairly simplistic at this stage: many of the direct manipulation interface elements which are currently common among graphics packages are missing due to development time constraints. As time permits, operations such as group operations, drag-and-drop operations, and in-place editing will be added.
Concept maps are an intuitive form of knowledge representation. While concept maps are useful for individual authors, their utility can be enhanced by making the concept mapping tools multi-user tools. As such, maps would be stored in a central repository where users could read, edit, and update them. Ideally, data integrity can be maintained by allowing multiple users to interact in real-time whenever more than one user accesses a particular map; that is, each users' state-changing activities would be broadcast to all the other concurrent users of the same map.
WWW through Netscape is a reasonable medium in which to embed such activity since it has the basic infrastructure to cover many of the requirements: support for Internet communication protocols, an API to embed "foreign" programs and closely integrate them with the browser, and a CGI interface to extend capabilities at the server end. A version of the KSIMapper program has been implemented as a Netscape plug-in for this purpose.
Concept maps can be used in informal (unstructured) forms as well as formal (structured) forms. But KSIMapper, by itself, can only handle informal, unstructured concept maps; it is not capable of constraining its maps as required by any of the graphical formalisms that exist, such KDraw and Conceptual Graphs. The Graphs program is designed for just such a purpose. While this program does not have a graphical user interface, it can be used to constrain an internally represented graph to conform to many graphical formalisms via a user-specifiable type lattice augmented by object attributes and "legality predicates".
The two programs, KSIMapper and Graphs, can be combined such that KSIMapper works as a graphical user interface for Constraint Graphs, and Constraint Graphs works to give KSIMapper a way to constrain its maps to emulate many formalisms. In this way, a flexible, multi-user, programmable concept mapping "shell" is formed.
It is still early in the life cycle of both programs. Exactly how easy it is to configure Graphs to handle other formalisms (other than its it initial test cases) remains to be seen. Efficiency considerations need to be addressed as well. Furthermore, the KSIMapper user interface is still quite rarefied and needs to be extended to handle several common direct manipulation features. Finally, it will be interesting to study whether such a system can simplify the transition between informal and formal systems.
Axelrod, R. (1976). Structure of Decision, Princeton, New Jersey: Princeton University Press. 1976.
Banathy, B.H. (1991). "Cognitive mapping of educational systems for future generations," World Futures, vol. 30, no. 1 pp. 5-17, 1991.
Booch, G. (1991). Object Oriented Design With Applications. Benjamin/Cummings, 1991.
Borenstein, N. and Freed, N. (1993). "MIME (Multipurpose Internet Mail Extensions) Part One: Mechanisms for Specifying and Describing the Format of Internet Message Bodies ", RFC 1521, http://www.cis.ohio-state.edu/htbin/rfc/rfc1521.html. September, 1993.
Borgida, A., Brachman, R. J., McGuiness, D. L., Resnick, L. A. (1989). "CLASSIC: A Structural Data Model for Objects." Proceeding of 1989 SIGMOD Conference on the Management of Data, New York, ACM Press, pp. 58-67.
Coad, P., North, D., and Mayfield, M. (1995). Object Models: Strategies, Patterns, and Applications. Yourdon Press Computing Series, 1995.
Cockburn, A., Thimbleby, H. (1995). "A Reflexive Perpective of CSCW." SIGCHI Bulletin, July, 1991. pp. 63-68.
Conklin, J., Begeman, M.L. (1987). gIBIS: A Hypertext tool for Team Design Deliberation." Hypertext'87, November, 198, pp. 247-2517.
Eden, C., Jones, S., and Sims, D. (1979). Thinking in Organizations, London: Macmillan. 1979.
Eklund, P. W., Leane, J. and Nowak C. (1993). "GRIT: Toward a Standard GUI for Conceptual Structures." Proceedings of the Second International Workshop on PEIRCE: A Conceptual Graphs Workbench, Laval University, Quebec, Canada, August 7, 1993.
Ellis, G., Levinson, R., (Eds.) (1992) Proceedings of the First International Workshop on PEIRCE: A Conceptual Graphs Workbench, Las Cruccs, New Mexico, 1992.
Gaines, B. R. (1991). "An Interactive Visual Language for Term Subsumption Languages." Proceedings of IJCAI-91, Sydney, Australia, August 24-30, 1991.
Gaines, B. R. (1993). "Situated Action Solution of a Resource Allocation Problem as a Classification Task Represented in a Visual Language." International Journal of Human-Computer Studies, 40(2). 1993. pp. 243-271.
Gamma, E., Helm, R., Johnson, R., and Vlissides, J. (1995). Design Patterns: Elements of Reusable Object-Oriented Software. Addison Wesley, Reading Mass. 1995.
Graesser, A.C. and Clark, L.F. (1985), Structures and Procedures of Implicit Knowledge, New Jersey: Ablex. 1985.
Grobe, M. (1995). "An Instantaneous Introduction to CGI Scripts and HTML Forms." http://kuhttp.cc.ukans.edu/info/forms/forms-intro.html. July 12, 1996.
Grudin, J. (1991). "Why Groupware Applications Fail: Problems in Design and Evaluation." Office: Technology and People, 4:3, 1989. pp. 245-264.
Hart, J.A. (1977). "Cognitive maps of three latin american policy makers," World Politics, vol. 30, no. 1 pp. 115-140, 1977.
Hayes, I. (Ed.) (1987). Specification Case Studies. Prentice-Hall, Englewood Cliffs, N.J. 1987.
Jia, X. (1995). "ZTC: A type checker for Z (version 2.02)." ftp://ise.cs.depaul.edu/pub/ZTC/. September 29,1996.
Kremer, R. (1993). "A Concept Map Based Approach to the Shared Workspace." MSc. Thesis, University of Calgary, Canada, June, 1993.
Kremer, R. (1994). "Concept Mapping: Informal to Formal." Proceedings of the Third International Conference on Conceptual Structures, Knowledge Represetnation Workshop, University of Maryland, 1994.
Kremer, R. (1995). "The Design of a Concept Mapping Environment for Knowledge Acquisition and Knowledge Representation." Proceedings of the Banff Knowledge Acquisition Workshop, Banff, Alberta, Canada. 1995.
Kremer, R. (1996a). "A Z Specification for the Formal Interpretation of Typed Graphs." http://www.cpsc.ucalgary.ca/~kremer/graphs/graphsZ2.html. September 30, 1996.
Kremer, R. (1996b). "A Z Specification for KRS using Typed Graphs." http://www.cpsc.ucalgary.ca/~kremer/graphs/KRS_Z.html. September 30, 1996.
Kremer, R.(1996c). " A Z Specification for the Conceptual Graphs based on of Typed Graphs." http://www.cpsc.ucalgary.ca/~kremer/graphs/CG_Z.html September 30, 1996.
Lambiotte, J. G., Dansereau, D. F., Cross, D. R., Reynolds, S. B. (1984). "Multirelational Semantic Maps." Educational Psychology Review, 1(4), 1984, pp. 331-367.
McNeese, M.D., Zaff, B.S., Peio, K.J., Snyder, D.E., Duncan, J.C., and McFarren, M.R. (1990). An Advanced Knowledge and Design Acquisition Methodology for the Pilot's Associate. Harry G Armstrong Aerospace Medical Research Laboratory, Wright-Patterson Air Force Base, Ohio. 1990.
Netscape Communications Corporation (1996a). "Developer Information: LiveConnect." Netscape Navigator 3.0 Developer Information, http://home.netscape.com/comprod/products/navigator/version_3.0/developer/mojava.html. September 28, 1996.
Netscape Communications Corporation (1996b). " Netscape JavaScript." http://home.netscape.com/comprod/products/navigator/version_2.0/script/index.html. September 28, 1996.
Nosek, J.T., Roth, I. (1990). "A Comparison of Formal Knowledge Representation Schemes as Communication Tools: Predicate Logic vs. Semantic Network." International Journal of Man-Machine Studies, 33, 1990. pp. 227-239.
Novak, J.D. and Gowin, D.B. (1984). Learning How To Learn, New York: Cambridge University Press. 1984.
Quillian, M.R. (1968), "Semantic memory," in Semantic Information Processing, M. Minsky, Editor. MIT Press: Cambridge, Massachusetts. p. 216-270, 1968.
Reisig, W. (1985). Petri Nets: An Introduction: Berlin: Springer. 1985.
Roseman, M. and Greenberg, S. (1996). "TeamRooms: Network Places for Collaboration." In Proceedings of the Computer Supported Cooperative Work Conference, Boston, Mass, November, 1996.
Sowa, J. F. (1984). Conceptual Structures: Information Processing in Mind and Machine. Addison-Wesley, Reading, Massachusetts, 1984.
Sun Microsystems Inc. (1996). "JavaSoft." http://java.sun.com/. September 25, 1996.
Tilton (1996). "Composing Good HTML."
http://www.cs.cmu.edu/~tilt/cgh/.