Distributed Artificial Intelligence Centre
(DAIC*)
Department of Mathematics, Statistics, and Computing Science
The University of New England, Armidale, 2351, N.S.W., AUSTRALIA
Email: lukose@peirce.une.edu.au
Tel.: +61 (0)67 73 2302 Fax.: +61 (0)67 73 3312
Abstract
In this paper, the author describes a graphically based executable conceptual modelling language called MODEL-ECS, for operationalising the Knowledge Analysis and Design Support (KADS) methodology. The main contribution of this paper is in the development of all the necessary constructs for modelling executable Problem Solving Methods (PSMs). These constructs include: conditional construct;while loop; repeat loop; and case construct. Knowledge passing between Knowledge Sources in a PSM is achieved using coreference links, and line of identity. The advantage of using MODEL-ECS comes from the expressibility provided by Conceptual Graphs, and the executability that is provided by the Executable Conceptual Structures.
1. INTRODUCTION 2. CONCEPTUAL GRAPHS 3. ACTOR 4. EXECUTABLE CONCEPTUAL STRUCTURES 4.1. Actor Graphs 4.2. Problem Maps 5. REFINEMENTS 6. COMPLEX MODELLING CONSTRUCTS 6.1. Sequential Construct 6.2. Conditional Construct 6.3. While Construct 6.4. Repeat Construct 6.5. Case Construct 7. CONCLUSION ACKNOWLEDGMENTS REFERENCES
1. INTRODUCTION
In recent years, many knowledge engineering methodologies have been proposed, as well as modelling languages based on these methodologies. Shaw and Gaines (1995) present an excellent overview of recent developments in knowledge engineering research, practice, theories, methodologies and tools. The modelling languages can be classified on two different dimensions. The first dimension being non-executable vs executable modelling languages. The scale in Figure 1 depicts the range of these modelling languages. The second dimension of classification is algorithmic vs graphical. Research and development along both of these dimensions have been the central focus in the mid-90's. Table 1 highlights some of the more popular algorithmic, as well as graphical modelling languages, that have appeared in recent years.
Figure 1: Modelling Languages for KADS
In recent years, several conceptual graph (Sowa, 1984) based modelling languages have been developed (Möller and Willems, 1995; Möller, 1995; and Lukose, 1995). All three were based on "extended" Conceptual Graphs (CG), with all of them have made several extensions to the standard CG theory. For example, MODEL-ECS uses Executable Conceptual Structures (ECS) (Lukose, 1994a; 1994b). Martin (1995), Mineau (1995), and Dieng (1995) also present knowledge acquisition, engineering and modelling methods using CG.
|
Methodology |
Modelling Language |
|
|
Algorithmic |
|
KADS (Wielinga, Schreiber and Breuker, 1992) |
MODEL-K (Karbach and Voß, 1993) |
|
Component of Expertise (Steels, 1990) |
TroTelC (Vanwelkenhuysen et al., 1990) |
|
Generic Tasks (Chandrasekaran and Johnson, 1993) |
TIPS (Punch and Chandrasekaran, 1993 |
|
KADS (Wielinga, Schreiber and Breuker, 1992) |
LISA |
|
|
Graphical Modelling |
|
DESIRE (Langevelde, et. al., 1992) |
CG-DESIRE (Möller and Willems, 1995) |
|
KADS (Wielinga, Schreiber and Breuker, 1992) |
[CG]->(ON)->[KADS] (Möller, 1995) |
|
KADS (Wielinga, Schreiber and Breuker, 1992) |
MODEL-ECS (Lukose,1995) |
Table 1: Knowledge Engineering Methodologies and associated Modelling Languages
Conceptual graphs are becoming the language of choice for implementing graphical modelling languages for some of the following reasons:
€ CG is a representation scheme that can effectively represent both the "abstract" as well as the more "specific" representation of the Problem Solving Methods (PSMs) modelled by the knowledge engineer;and
€ CG together with ECG has been demonstrated in Lukose et al. (1995a) as being able to represent, not only the abstract and specific view of the PSMs, but also that the final conceptual model is executable.
CGs can be used as a uniform representation language for representing Task Models, Models of Cooperation, Expertise Model, and finally the Conceptual Model (for the KADS methodology in particular) (Lukose, et al., 1995b). But, one must not be mislead into believing that CG and ECS is an all good, and all encompassing, representational scheme that solves all modelling problems. There are several crucial research problems to be solved to enable the liberal exploitation of the MODEL-ECS for modelling and prototyping. Firstly, the ability to handle conditional control structures, case constructs, and loops (i.e., repeat loops, while loops, etc.). Secondly, the ability to handle refinements of the knowledge sources (i.e., or Actor Graphs in the MODEL-ECS term) and knowledge passing. Apart from this, there is certainly the issue of having an efficient implementation of a CG-processor to realise rapid prototyping.
In this paper, the author attempts to describe in detail the MODEL-ECS. This involves firstly describing how conceptual graphs and the actor formalism are used to build Actor Graphs, which form the most primitive executable structure. This is then followed with a description of the syntax and semantics necessary for the modelling of the conditional constructs and loops in MODEL-ECS. MODEL-ECS is can be used effectively as a modelling language for the KADS methodology (Wielinga, Schreiber, and Breuker, 1993)!. Examples of complex PSMs using MODEL-ECS are also illustrated in this paper.
The outline of this paper is as follows. In Section 2, the author describes the necessary components of Conceptual Graphs (abstractions, type definition, and relation definition). This is followed by a description of the Actor formalism in Section 3. Section 4 describes the synergy of Conceptual Graphs with Actor formalism to form Actor Graphs (i.e., Executable Conceptual Structures). This section also describes how Actor Graphs can be partially ordered using temporal conceptual relations to form Problem Maps. Section 5 describes refinement with the use of nested Problem Maps. This section also describes the use of coreference links and lines of identity to facilitate knowledge passing between Knowledge Sources within a context; and between different contexts, while a complex Problem Map is executing. Section 6 describes the necessary syntax and semantics for realising complex modelling constructs like conditional construct; repeat loop; while loop; and case construct. Detailed descriptions of each of these constructs, together with examples of sophisticated PSMs using these constructs, are also provided in this section. Finally, Section 7 concludes this paper by describing the future direction of this research.
2. CONCEPTUAL GRAPHS
Conceptual graphs are finite, connected, bipartite graphs. They are finite because any graph in an agent's memory (i.e., human or computer) can have only a finite number of concepts and conceptual relations. They are connected because two parts that were not connected would simply be called two conceptual graphs. They are bipartite because there are two different kinds of nodes (i.e., concepts and conceptual relations), and every arc links a node of one kind to a node of the other kind (Sowa, 1984, pp. 72). In diagrams (i.e., display form), a concept is drawn as a box, a conceptual relation as a circle, and an arc as an arrow that links a box to a circle. For example, in diagrams, a conceptual graph representation of a natural language sentence "Dickson went to Calgary by plane" is as shown in Figure 2.
Figure 2: Diagram representation of a simple conceptual graph
The same conceptual graph can be represented in linear form. In linear form, the boxes are abbreviated with square brackets, and the circles with rounded parentheses. Thus, the conceptual graph shown in Figure 2 can be represented in linear form as shown below:
[GO] -
-> (AGNT) -> [PERSON: Dickson]
-> (INST) -> [PLANE]
-> (DEST) -> [CITY: Calgary]
<- (PAST).
First-order graphs maps into first-order logical formula. For example, the logical formula representation of the above conceptual graphs is shown below:
x
A definition can equate an entire graph with a name or type label.
Type definitions provide a way of expending a concept in primitives,
or contracting a concept from a graph of primitives. Definitions can
specify a type in two different ways: by stating necessary and
sufficient conditions for the type, or by giving a few examples and
saying that everything similar to these belongs to the type.
Conceptual Graphs support type definition by genus and
differentiae, as well as schemata and
prototypes. Both methods are based on abstractions, which are
canonical graphs# with one or more concepts designated as formal
parameters. An n-adic abstraction, 
a1,.....,anu,
consists of a canonical graph u, called the body, together
with a list of generic concepts
a1,.....,an in u, called
the formal parameters. A generalisation hierarchy is defined over
abstractions.
Definition 1: A type definition declares that a type
label t is defined by a monadic abstraction
a u. It is written,
type t(a) is u. The body u is
called the differentia of t, and type(a) is
called the genus of t.
An example of a type definition for OBTAIN is shown in Figure 3.
Figure 3: Type Definition for concept type "OBTAIN"
Definition 2: A relation definition, written
relation
t(a1,....,an) is u,
declares that the label t for a conceptual relation is defined
by an n-adic abstraction, a1,....,anu. The
body u is called the relator of t.
Figure 4 and 5 shows the relation definition for two temporal relations (i.e., FINISH_BEFORE_START (FBS) that indicates sequence, and START_WHEN_START (SWS) to indicate concurrency).
Figure 4: Relation Type Definition for FBS
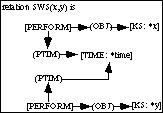
Figure 5: Relation Type Definition for SWS
3. ACTOR
There two types of actors (objects). They are the class (type) actor and the instance actor. Class actors are defined as abstractions. An actor hierarchy is defined over all the class actors. It responds to an incoming message by executing a method corresponding to the message. A detailed description of each of the components of the Actor (i.e., Class Actor or Instance Actor) is beyond the scope of this paper. Interested readers may refer to Lukose (1993) for a detailed discussion.
Definition 3: An actor type (or class) t is
defined as an n-adic abstraction m1, m2, ...,
mn u, written as the actor t (
m1, m2, ..., mn
) is u. The body u is called the "actor", while
m1, m2, ..., mn
represents the messages that the "actor" can respond to. If r
is an actor of class t, then the message handler in r
can handle n different messages (i.e., m1,
m2, ..., mn), represented by n
different methods in "actor" u.
An example for actor class (type) for OBTAIN is shown in Figure 6.
Figure 6: Class Actor for "OBTAIN"
4. EXECUTABLE CONCEPTUAL STRUCTURES
Actor Graphs are the most primitive Executable Conceptual Structures. Actor Graphs use conceptual graphs to represent the declarative knowledge associated with an inference step, and an actor script to represent the procedural knowledge (Lukose, 1993).
Definition 4: An Actor Graph labelled t is
defined as a dyadic abstraction a u1 m u2, where
type(a) is the genus of t, the body
u1 is the differentia of t, and
m is the message that will invoke the main method
described in the "actor" u2.
Figure 7 depicts a graphical representation of the Actor Graph. Actor Graphs adopt the semantics of the STRIPS architecture (Fikes and Nilsson, 1971). Each Actor Graph has, associated with it, sets of conceptual graphs representing the "precondition", "postcondition" and "delete" lists. The actor associated with an Actor Graph is made up of three parts: short term memory; long term memory; and main methods. The short term memory is used to record current values associated with the problem domain. The long term memory is used to store the precondition, postcondition and delete lists. The main method section represents the set of methods that the actor is able to call upon. The precondition graphs represent the knowledge which must exist for the inference step represented by the Actor Graph to be executed. The postcondition graphs represent the new knowledge which is created by the inference. Any graphs in the delete list represent knowledge which no longer holds as a result of the inference step.
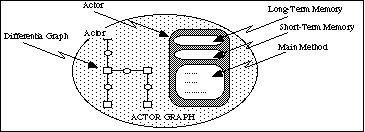
Figure 7: Graphical Representation of an Actor Graph
By combining the differentia of the type definition for OBTAIN (i.e., Figure 3), with the actor for OBTAIN (i.e., Figure 6), actor graph for OBTAIN is formed as shown in Figure 8.
Figure 8: Actor graph for OBTAIN
The Problem Map is an executable conceptual structure which can be used to represent task knowledge in a KADS model. A Problem Map is formed by specifying a partial temporal ordering of the Actor Graphs (Cross and Lukose, 1994) which represent the primitive inference steps.
Definition 5: A Problem Map labelled t is
defined as a n-adic abstraction
v1,..,vn
w1,...,wm u, where u is the
conceptual graph (i.e., body) representing the Problem Map,
v1,..,vn which is in turn the set
of conceptual graphs representing the initial state, while
w1,...,wm is the set of graphs
representing the final state.
Two relations are used to specify the partial temporal ordering of the Actor Graphs: FINISH_BEFORE_START (FBS) and START_WHEN_START (SWS). The (FBS) relation is used to represent a temporal constraint between two Actor Graphs. The (SWS) relation is used to link two Actor Graphs when there is no temporal constraint between them (Cross and Lukose, 1994). Consider the Problem Map shown below, which is made up of six Actor Graphs (i.e., ag1,...., ag6). These Actor Graphs are referent to a meta level concept [KS], which stands for "knowledge source".
[KS:ag1]->(FBS)->[KS:ag2]->(FBS)->[KS:ag3]
->(FBS)->[KS:ag4]->(SWS)->[KS:ag5]
->(SWS)->[KS:ag6]
PSMs are represented using Problem Maps in MODEL-ECS. The simplest Problem Map is a single Knowledge Source. For example, consider a Problem Map that is made up of only one knowledge source (i.e., OBTAIN). This Problem Map is represented as shown below:
[KS: [obtain] -
-> (OBJ) -> [ENTITY:*m]
-> (SRCE) -> [PLACE:*n]
-> (AGNT) -> [ENTITY:*o]
-> (RCPT) -> [ENTITY:*o]
].
Usually, a Problem Map is composed of more than one knowledge source, connected by the temporal conceptual relations FBS or SWS, as described in subsection 4.2. For example, the Problem Map representing the PSM for Diagnosis of an Audio System (Lukose, 1995) is shown in Figure 9.
One of the main advantages of using Problem Maps to represent PSMs is its ability for information hiding. That is, the ability to represent a Problem Map within another Problem Map. To enable nesting, the conceptual relations FBS and SWS are extended to point from or into not only Knowledge Sources (i.e., [KS]), but, also to Problem Maps (i.e., [PM]). The following conventions are then available to MODEL-ECS:
(1) [KS: *a] -> (FBS) -> [KS: *b]
Here both a and b are Knowledge Sources. This construct is similar to all the examples of Problem Maps described earlier. There is no nesting in this form of construct. Here the execution of Knowledge Source a has to be completed before commencing the execution of the Knowledge Source b.
(2) [KS: *a] -> (FBS) -> [PM:*b]
Here, a is a Knowledge Source, while b represents a Problem Map with one or more Knowledge Sources. This construct states that the execution of Knowledge Source a has to be completed before commencing the execution of the Problem Map b.
(3) [PM: *a) -> (FBS) -> [KS: *b]
Here, a is a Problem Map, and b is a Knowledge Source. This construct states that the execution of the Problem Map a has to be completed before commencing the execution of the Knowledge Source b.
(4) [PM: *a] -> (FBS) -> [PM: *b]
Here, both a and b are Problem Maps. This construct states that the execution of Problem Map a has to be completed before the execution of Problem Map b can commence.
(5) [KS: *a] -> (SWS) -> [KS: *b]
Here, both a and b are Knowledge Sources. In this form of construct, there is no nesting. This construct states that the Knowledge Source a can be executed at the same time as Knowledge Source b is being executed.
(6) [KS:*a] -> (SWS) -> [PM: *b]
Here, a is a Knowledge Source, while b is a Problem Map that may be made up of one or more Knowledge Sources. This construct states that Knowledge Source a can be executed at the same time as Problem Map b is being executed.
(7) [PM: *a] -> (SWS) -> [KS: *b]
Here, a is a Problem Map, while b is a Knowledge Source. This construct states that Problem Map a can be executed at the same time as Knowledge Source b.
(8) [PM: *a] -> (SWS) -> [PM: *b]
Here both a and b are Problem Maps. This constructs states that you can execute Problem Map a at the same time as executing Problem Map b.
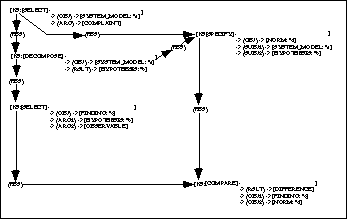
Figure 9: PSM for Diagnosis of an Audio System
The level of nesting is not necessarily limited to one, as shown is the above constructs. It is possible to have n-levels of nesting, as shown below:
[PM:[KS:*w] -
->(FBS)->[PM:[KS:*x]->(SWS)->[KS:*y]
]
]->(FBS)->[KS:*z]
We could re-represent the above Problem Map as shown below:
[PM:*b]->(FBS)->[KS:*z] - nesting at Depth 0
where z is a Knowledge Source, while b is another Problem Map as shown below:
[KS:*x]->(SWS)->[KS:*y] - nesting at Depth 1
There is one major issue to be addressed with nested Problem Maps. That is, the flow of information from a sub-component (i.e., concepts) of a knowledge source nested within a Problem Map to concepts in another Problem Map or Knowledge Sources in different context or at different levels of nesting. Knowledge passing of this form is achieved by the use of context, coreference links and line of identity (Sowa, 1984). Definition 6, 7 and 8 briefly describes coreference link, context and line of identity, respectively.
Definition 6: Coreference links@ show which concepts refer to the same entities. In linear form representation of conceptual graphs, coreference links are represented using variables.
For example, consider the following conceptual graph:
[OBTAIN]-
->(AGNT)->[PERSON:*a] -
<-(AGNT)<-[LIVE]-
->(LOC)->[PLACE Loughborough]
->(OBJ)->[CAR:@2342]->(ATTR)->[RED]
->(SRCE)->[PLACE:London]
->(RCPT)->[PERSON: *a].
Here, the agent of OBTAIN is the same as the recipient of OBTAIN. The variable a is used to represent the coreference link between the two concept PERSON in the above conceptual graph.
Definition 7: The outermost context is the collection of all conceptual graphs that do not occur in the referent of any concept. If a concept or conceptual graph occurs in the outermost context, it is said to be enclosed at depth 0. If a context y occurs in a context x, then x is said to dominate y. If y dominates another context z, then x also dominates z. The outermost context dominates all other contexts& .
Definition 8: A line of identity is a connected, undirected graph g whose nodes are concepts and whose arcs are pairs of concepts, called coreference links*.
Using the coreference links, context, and line of identity, knowledge passing can be conducted successfully between Problem Maps within a context, or between Problem Maps in different contexts. For example, the Problem Map shown in Figure 10 shows a representation of a simple knowledge passing.
In the example shown in Figure 10, the concept PLACE which is the object of SELECT (in context depth 2) is identical to the PLACE which is the object of SURVEY (in context depth 3). These two concepts (i.e., PLACE) are linked to each other by the concept PLACE (in context depth 1), by line of identity. Similarly, the concept HOUSE which is the object of BUILD is linked to the concept HOUSE which is the object of DESIGN by a different line of identity.
With the availability of nesting within Problem Maps, and the ability for knowledge passing, MODEL-ECS is ready to tackle more complex modelling constructs. These constructs are mainly to do with conditions and loops. Section 6 describes the necessary vocabulary to model complex constructs. This section also describes all the necessary complex modelling constructs which enable MODEL-ECS to be liberally exploited for building executable conceptual models.
Figure 10: Knowledge Passing between context by using line of identity
6. COMPLEX MODELLING CONSTRUCTS
The main ingredients for building complex modelling constructs are: Actor Graph, Problem Map, conceptual relations to enable expression of sequence, and special purpose Actor Graphs for expressing condition and iteration. Conceptual Relations, and special purpose Actor Graphs necessary for building complex Problem Maps, are listed in Table 2.
Table 2: Conceptual Constructs
Assuming that 
and 
denote predicates (i.e., conceptual
graphs) and 
and 
denote Problem Maps, the
above conceptual constructs can be used to construct simple Problem
Maps shown in Table 3.
Table 3: Syntax and Semantics of Modelling Constructs
Using the simple modelling constructs outlined in Table 3, we are
able to build more complex modelling constructs as shown in Table 4.
Again, assume that and are predicates (i.e., conceptual
graphs), while and are Problem Maps.
Table 4: Modelling Constructs representation using Executable Conceptual Structures
Modelling Construct: ; ; .......
MODEL-ECS: [PM:] -> (FBS) -> [PM:]
-> (FBS) -> ........
This is the simplest form of nested Problem Map. Here, both
and are nested Problem Maps, where the execution of
must be completed before the execution of
Modelling Construct: if
Here, is a conceptual graph representing
the condition for executing Problem Maps a or . This construct
will simply execute Problem Map if
is true, if not, it will execute the Problem Map . For example,
consider a Problem Map that first searches for a place (from a set of
available places), then if it has found a place, it will carry out
the land surveying process and the designing of a house. If not,
control is returned back to the search process. Thus, here we are
confronted with a situation which, based on a condition, control will
be passed to different sections of the Problem Map. Modelling a
Problem Map of this type is not difficult. Using the "if the a else "
construct, where and are the two sub-Problem
Maps, and represents the condition, we are
able to model a complex Problem Map as shown in Figure 11. In this
Problem Map is represented
by the following conceptual graph:
[FOUND] -> (OBJ) -> [PLACE] g1
The Problem Map can be represented in linear form in the following manner:
[KS: g3] -> (FBS) -> [PM: g4] g2
were g3 represents the Knowledge Source SEARCH as shown below:
[SEARCH] -> (OBJ) -> [PLACE: *x] g3
and g4 represents a the conditional Problem Map, as shown below:
[PM: { g5, g6} ] g4
where g5 is a nested Problem Map as shown below:
[KS: TRUE_TEST: g1] ] -> (FBS) -> [PM: g7] g5
and g6 is also a nested Problem Map as shown below:
[KS: [FALSE_TEST: g1] ] -> (FBS) -> [KS:*] g6
Problem Map g7 is shown below:
[KS: g8] -> (SWS) -> [KS: g9] g7
where g8 is the Knowledge Source shown below:
[SURVEY] -> (OBJ) -> [PLACE: *x] g8
and finally, g9 is a following Knowledge Source:
[DESIGN] -> (OBJ) -> [HOUSE] g9
The Knowledge Source TRUE_TEST will check the existence of this conceptual graph in the state space. If the Knowledge Source SEARCH has successfully found a place, an image of g1 will be inserted into the state space. Thus, when the control is passed to TRUE_TEST, it will be able to successfully identify the existence of an image of g1, and thus control is passed to the Problem Map that performs the surveying and designing process. On the other hand, if TRUE_TEST is unable to find an image of g1 in the state space, then control is passed to FALSE_TEST (which, in this case, will not be able to find an image of g1 in the state space, thus returning a value "true"). Thus, control is passed to the Knowledge Source which is linked to SEARCH via a line of identity. Therefore, control is once again passed to the Knowledge Source called SEARCH. The execution of this Problem Map will continue until it finds a place, and successfully carries out the survey and design process.
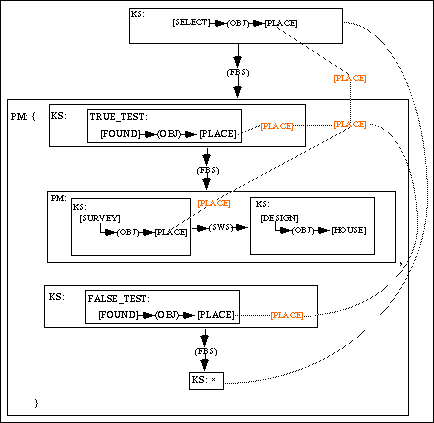
Figure 11: MODEL-ECS representation of Conditional Construct
Modelling Construct: while
The "while do "
construct is a nested Problem Map. This construct simply repeats
executing the Problem Map a as long as the conceptual graph
represented by is true. This
construct is made up of two knowledge sources (i.e.,
TRUE_TEST, and FALSE_TEST), and a complex Problem Map
(i.e., [PM: ]). The functions of each of the
knowledge sources are as follows:
€ the knowledge source TRUE_TEST checks the "state space" to determine whether f exists in the "state space", and if so, execution simply proceeds to the next knowledge source in the sequence (i.e., in the above construct, execution proceeds to the Problem Map [PM: a]); and
€ the knowledge source FALSE_TEST checks the "state space" to ensure that f does not exist in the "state space", and if so, execution simply proceeds to the next knowledge source (i.e., in the above case, the execution terminates at this point).
To illustrate modelling the "while do
" construct, the author will utilise a variation of
the Propose-and-Revise (P&R) PSM which was described in Marcus et
al. (1988). The P&R PSM constructs a solution to a problem by
iteratively extending and revising partial solutions. The assumption
being that the solution can be described in terms of assignments of
values to parameters, and that the PROPOSE phase
can be carried out by applying a domain dependent knowledge source
which allows the derivations of values of unbound parameters from
parameters which have already been assigned (Zdrahal and Motta,
1995). The P&R PSM used in this paper is adopted from Fensel
(1995), and is called the Select-Propose-Check-Revise Method
(SPCR-Method). It is depicted in Figure 12. Descriptions of
the four sub-tasks are as follows:
€ the SELECT sub-task chooses the parameter which should be processed next;
€ the PROPOSE sub-task proposes a value for the selected parameter;
€ the CHECK sub-task checks the currently given partial assignment (i.e., the old one which is enriched by the new parameter-value pair) as to whether it fulfils the given constraints; and
€ the REVISE sub-task corrects the partial assignment if constraint violations were detected by the CHECK sub-task.
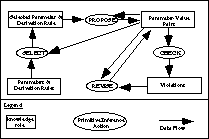
Figure 12: Select-Propose-Check-Revise Method (adopted from Fensel (1995))
The MODEL-ECS equivalent of the SPCR-Method is shown by the
Problem Map depicted in Figure 13. It consists of three primitive
inference structures (i.e., SELECT, PROPOSE, and
CHECK), a complex inference structure (i.e., REVISE),
and a complex modelling construct (i.e., Problem Map representing the
"while do "
modelling construct).
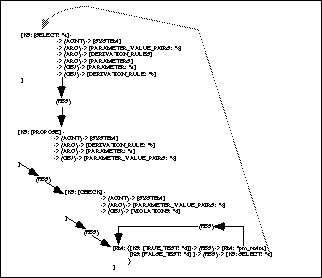
Figure 13: MODEL-ECS equivalent of the SPCR-Method
The interesting part of the Problem Map shown in Figure 13 is the
complex modelling construct that represents the "while do " construct. It is
reproduced below:
[PM:{[KS:[TRUE_TEST:*d]]->(FBS)->[PM:*pm_revise]->(FBS)->[PM:*],
[KS:[FALSE_TEST:*d]]->(FBS)->[KS:[SELECT:*e]]
}
]
Here, the author did not reproduce the line of identity
(i.e., coreference links) that links the knowledge source
SELECT in the context of depth 2, to the outermost
context. The function of the "while
do " construct is as follows: The
SYSTEM firstly checks the "state space" to determine whether
violations (i.e., represented by the co-reference link *d) exist. If
so, execution proceeds to the next knowledge source. In this case, it
is a complex Problem Map (i.e., pm_revise). When the execution
of the nested Problem Map pm_revise is completed, control is
once again passed to the knowledge source TRUE_TEST. This
repeat-loop terminates only when TRUE_TEST returns a false
answer. When this happens, it indicates that appropriate revisions
have been done to eliminate all the violations identified by the
Knowledge Source CHECK. The construct passes control onto the
knowledge source FALSE_TEST, to make sure that there are no
violations (thus, returning a value "true"), then, control finally
flows back to the knowledge source SELECT, which will select
the next set of parameter and derivation rules; and the process
continues. The SPCR-Method terminates when there are no more
parameter and derivation rules to select.
Modelling Construct: repeat
The "repeat until " is
another form of complex modelling construct that is based on nested
Problem Maps. In this construct, the Problem Map is executed
first, then, a FALSE_TEST is performed on the predicate . If the FALSE_TEST returns
"true" (i.e., which indicates that an image of the conceptual graph
is not found in the state space), the
control is passed to the Problem Map . This loop continues
until FALSE_TEST returns "false", in which case control is then
passed to TRUE_TEST (which will return "true", since we are
testing the same ). For example,
in Figure 14, the condition is represented
by the following conceptual graph:
[FOUND] -> (OBJ) -> [PLACE] g1
This Problem Map can be represented in linear form as shown below:
[PM: g3] -> (FBS) -> [PM: {g4 , g5}] g2
where g3 is a Problem Map (in this example, it is a Problem Map with only one
Knowledge Source called SELECT), which is represented as shown below:
[KS: [SELECT] -> (OBJ) -> [PLACE] ] g3
and finally, g4 and g5 are as shown below:
[KS: [FALSE_TEST: g1 ] ]-> (FBS) -> [PM: g3] g4 [KS: [TRUE_TEST: g1 ] ] g5
Figure 14: MODEL-ECS representation of the Repeat Construct
Modelling Construct: case
This construct is also based on the nested Problem Map. Here, we
have a situation where Problem Map is executed if condition
is "true". If it is "false", the
condition is tested. If it returns "true" then
Problem Map will be executed. If the test for
both of these conditions return "false", then this whole Problem Map
returns control to the next executable structure. An example of the
MODEL-ECS representation of this form of complex modelling construct
is shown in Figure 15. In this example, the two conditions are
represented by conceptual graph g1 and
g2, respectively:
[FOUND] -> (OBJ) -> [PLACE] g1 [COMPLETE] -> (OBJ) -> [HOUSE_PLAN] g2
In linear form, the Problem Map can be represented as follows:
[PM: {g4, g5} ] g3
where g4 is a Problem Map shown below:
[KS: [TRUE_TEST: g1] ] -> (FBS) -> [PM: g6] g4
and g5 is another Problem Map as shown below:
[KS: [TRUE_TEST: g2] ] -> (FBS) -> [PM: g7] g5
The Problem Map g6 is shown below:
[KS: g8] -> (SWS) -> [KS: g9] g6
The Problem Map g7 consist of only one Knowledge Source, shown below:
[KS: g10] g7
Finally, the Knowledge Sources, g8, g9, and g10, are all shown below:
[SURVEY] -> (OBJ) -> [PLACE] g8 [DESIGN] -> (OBJ) -> [HOUSE] g9 [BUILD] -> (OBJ) -> [HOUSE] g10
The execution of this problem map is as follows. If the agent has found a suitable place (i.e., condition graph represented by graph g1), then carry out the land survey (represented by Knowledge Source g8) and house design (i.e., represented by Knowledge Source g9) process; if not, then check if the house plan is completed (i.e., condition represented by graph g2). If so, then proceed to build the house (i.e., represented by Knowledge Source g10). If not, then control will be passed to the next executable structure (in this example, there is no other executable structure, thus the execution of the Problem Map will terminate).
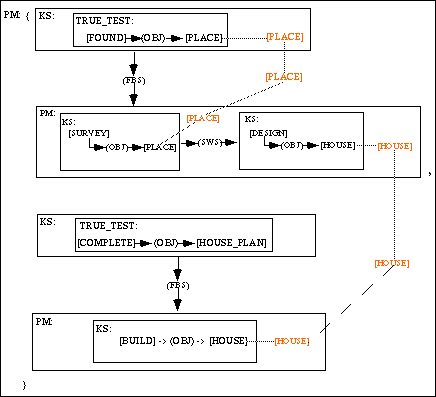
Figure 15: MODEL-ECS representation of Case Construct
In this paper, the author described the Executable Conceptual Structures necessary to build primitive and complex modelling constructs for the graphical based executable conceptual modelling language called MODEL-ECS. The major contribution of this paper lies in the development of some necessary extensions to MODEL-ECS, to enable a formal modelling process for building complex PSMs. The extensions described in this paper are the conditional modelling constructs, and loops constructs (i.e., repeat loops, while loops, case constructs etc). In this paper, the author describes the syntax and semantics of primitive and complex modelling constructs of MODEL-ECS. This paper also provided examples of using these constructs to model complex PSMs. To facilitate complex modelling, nested Problem Maps are necessary. With nesting, the need from knowledge passing between Knowledge Sources within a context, as well as between contexts is essential to enable information transfer to take place while the Problem Map is being executed. Knowledge passing in complex Problem Maps is achieved using coreference links and line of identity.
By using MODEL-ECS, knowledge engineers can build executable versions of the KADS Conceptual Model, without carrying out the Design Modelling Process. This capability is essential for rapid-prototyping. Since the Conceptual Models are executable, the knowledge engineer will be able to verify the correctness of the model by executing it. Further, the knowledge engineer could easily modify the Conceptual Model with the use of Canonical Formation Rule (Sowa, 1984).
The future direction of this research involves carrying out evaluation processes to identify the limitations of the modelling constructs described in this paper. The next area of development is to associate each knowledge source with a representative "icon". When this is done, the knowledge modeller will not have to deal to conceptual graphs any longer. Thus, conceptual modelling tasks will involve the use of meaningful "icons" (i.e., which can be executed). This form of extension is not only useful for modelling PSMs, but it is also useful as a visual programming tool, and most importantly for enterprise modelling. This is just a brief indication of the future direction of our research.
We would like to take this opportunity to thank all the members of the Distributed Artificial Intelligence Centre (DAIC) at The University of New England for all their contributions in developing the modelling constructs described in this paper. Also, a very special thanks to Ms Meg Vivers for checking English expression in this paper.
Chandrasekaran, B., and Johnson, T. (1993). Generic tasks and Tasks Structures: History, Critique and New Directions, in J.M. David, J.P. Krivine, and R. Simmons (Eds.), Second Generation Expert Systems, Springer Verlag, Berlin, Germany.
Cross, T. and Lukose, D. (1994). The representation of non-linear hierarchical executable plans, in Proceedings of the 1st Australian Workshop on Conceptual Structures, Armidale, N.S.W., Australia.
Dieng, R. (1995). Specifying a Cooperative System through Agent-Based Knowledge Acquisition, in Proceedings of the 9th Banff Knowledge Acquisition For Knowledge-Based Systems Workshop, Banff Conference Centre, Banff, Alberta, Canada.
Fensel, D. (1995). Assumptions and Limitations of a Problem Solving Method: A Case Study, in Proceedings of the 9th Banff Knowledge Acquisition For Knowledge-Based Systems Workshop, Banff Conference Centre, Banff, Alberta, Canada.
Fensel, D., Angele, J., and Landes, D. (1991). Knowledge Representation and Acquisition Language (KARL), in Proceedings of the 11th International Workshop on Expert Systems and Their Applications (Volume: Tools and Techniques), Avignon, France.
Fikes, R. E., and Nilsson, N. J. (1971). STRIPS: A new approach to the application of theorem proving to problem solving, Artificial Intelligence 2(3-4).
Karbach, W., and Vob, A. (1993). MODEL-K for prototyping and strategic reasoning at the knowledge level, in J.M. David, J.P. Krivine, and R. Simmons (Eds.), Second Generation Expert Systems, Springer Verlag, Berlin, Germany.
Langevelde, I.A., van, Philipsen, A.W., and Treur, J. (1992). Formal specification of compositional architectures, in B. Neumann (ed.), in Proceedings of the 10th European Conference on Artificial Intelligence, ECAI'92, John Wiley & Sons, Chichester.
Linster, M. (1993). Using OMOS to Represent KADS Conceptual Model, in Schreiber, G., Wielinga, B., and Breuker, J., (Eds.), KADS: A Principles Approach to Knowledge-Based System Development, Academic Press.
Lukose, D. (1993). Executable Conceptual Structures, in G.W. Mineau, B. Moulin and J.F. Sowa (Eds.), Conceptual Graphs for Knowledge Representation, Lecture Notes in Artificial Intelligence (699), Springer- Verlag, Berlin, Germany.
Lukose, D. (1994a). Planning Knowledge Acquisition Techniques and Mechanisms, in Proceedings of the ICCS'94 Workshop on Knowledge Acquisition using Conceptual Graphs, M.L. Mugnier, M. Willims, B. Gaines and D. Lukose (Eds.), Maryland, USA.
Lukose, D. (1994b). Problem Map: A Hybrid Knowledge Representation Scheme, In Proceedings of the 7th Australian Joint Conference on Artificial Intelligence, C. Zhang, J. Debenham, and D. Lukose (Eds.), Armidale, N.S.W., Australia.
Lukose, D. (1995). Using Executable Conceptual Structures for Modelling Expertise, in Proceedings of the 9th Banff Knowledge Acquisition For Knowledge-Based Systems Workshop, Banff Conference Centre, Banff, Alberta, Canada.
Lukose, D., Cross, T., Munday, C., and Sobora, F. (1995a). Operational KADS Conceptual Model using Conceptual Graphs and Executable Conceptual Structures, in Proceedings of the International Conference on Conceptual Structures (ICCS'95), USA.
Lukose, D., Mineau, G., Mugnier, M-L., Möller, J-U., Martin, P., Kremer, R., and Zarri, G.P. (1995b). Conceptual Structures for Knowledge Engineering and Knowledge Modelling, in Proceedings of the International Conference on Conceptual Structures, USA.
Marcus, S., Stout, J., and McDermott, J. (1988). VT: An Expert Elevator Designer that uses Knowledge-Based Backtracking, AI Magazine 9(1).
Martin, P. (1995). Knowledge Acquisition using Documents, Conceptual Graphs and a Semantically Structured Dictionary, in Proceedings of the 9th Banff Knowledge Acquisition For Knowledge-Based Systems Workshop, Banff Conference Centre, Banff, Alberta, Canada.
Mineau, G.W. (1995). Establishing a Semantic Basis: Toward the Integration of Vocabularies, in Proceedings of the 9th Banff Knowledge Acquisition For Knowledge-Based Systems Workshop, Banff Conference Centre, Banff, Alberta, Canada.
Möller, J-U. (1995). Operationalisation of KADS Models by using Conceptual Graph Modules, in Proceedings of the 9th Banff Knowledge Acquisition For Knowledge-Based Systems Workshop, Banff Conference Centre, Banff, Alberta, Canada.
Möller, J-U., and Willems, M. (1995). CG-DESIRE: Formal Specification Using Conceptual Graphs, in Proceedings of the 9th Banff Knowledge Acquisition For Knowledge-Based Systems Workshop, Banff Conference Centre, Banff, Alberta, Canada.
Punch, W.F., and Chandrasekaran, B. (1993). An Investigation of the Roles of Problem-Solving Methods in Diagnosis, in David, J.M., Krivine, J.P., and Simmons, R., (Eds.), Second Generation Expert Systems, Springer Verlag, Berlin, Germany.
Schreiber, G., Wielinga, B., and Breuker, J. (1993). KADS: A Principled Approach to Knowledge-Based System Development, Academic Press, London, UK.
Shaw, M.L.G., and Gaines, B.R. (1995). Knowledge and Requirements Engineering, in Proceedings of the 9th Banff Knowledge Acquisition For Knowledge-Based Systems Workshop, Banff Conference Centre, Banff, Alberta, Canada.
Sowa, J.F. (1984). Conceptual Structures: Information Processing in Mind and Machine, Addison Wesley, Reading, Mass., USA.
Steels, L. (1990). Components of Expertise, AI Magazine, 11(2).
van Harmelen, F., and Balder,1990). Mapping a Knowledge Level Analysis onto a Computational Framework, in Proceedings of the 9th European Conference on Artificial Intelligence, London, Pitman Publishing.
Voß, A., and Karbach, W. (1993). MODEL-K: Making KADS Run, in G. Schreiber, B. Wielinga, and J. Breuker (Eds.), KADS: A Principles Approach to Knowledge-Based System Development, Academic Press.
Wetter, T. (1990). First-order logic foundation of the KADS conceptual model. in B. Wielinga, J. Boose, B. Gaines, G. Schreiber, and M. van Someren (Eds.), Current Trends in Knowledge Acquisition, Amsterdam, The Netherlands, IOS Press.
Wielinga, B., Schreiber, A.T., and Breuker, J.A. (1992). KADS: A Modelling Approach to Knowledge Engineering, in The KADS Approach to Knowledge Engineering Special Issue, Knowledge Acquisition, 4(1), Academic Press, London, UK.
Wielinga, B., Schreiber, A.T., and Breuker, J.A. (1993). Modelling Expertise, in KADS: A Principled Approach to Knowledge-Based System Development, Academic Press, London, UK
Zdrahal, Z., and Motta, E. (1995). An In-Depth Analysis of Propose & Revise Problem Solving Methods, in Proceedings of the 9th Banff Knowledge Acquisition For Knowledge-Based Systems Workshop, Banff Conference Centre, Banff, Alberta, Canada, February 26 - March 3, 1995, Paper No: 38.
------------------------------------
* To find out more about DAIC, refer to our URL: http://turing.une.edu.au/~daic/
! For details on KADS methodology, refer to Schreiber et al., (1993).
# Certain conceptual graphs are canonical. New graphs may become canonical or be canonised by any of the following three processes: perception; formation rules; or insight.
@ In a sentence, these links are expressed as pronouns and other anaphoric references. Refer to Sowa (1984, pp. 10).
& Refer to Sowa (1984, pp. 141) for more details on context.
* Refer to Sowa (1984, pp. 142) for details on line of identity.