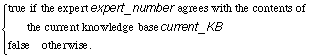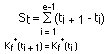Deriving Formal Parameters for Comparing Knowledge Elicitation
Techniques Based on Mathematical Functions.
Rodrigo Martinez-Bejar*, Richard
Benjamins**, Fernando Martin*** and Victor
Catillo*
*Spanish Council for Scientific Research -
CEBAS, Avda. La Fama, 1, C.P. 30080, Murcia, Spain. Email:
rodrigo,victor@natura.cebas.csic.es
**Department of Social Science Informatics,
University of Amsterdam, Roetersstraat 15, 1018 WB Amsterdam, The Netherlands. Email:
richard@swi.psy.uva.nl
***Department of Computing Sciences,
University of Murcia, Murcia, Spain.
Email:fmartin@dif.um.es
The knowledge elicitation process has a considerable influence on the
quality of the knowledge-based system to be developed. Moreover, because
knowledge elicitation is an important cost-determining factor, a good
elicitation technique should reveal the relevant knowledge in the minimum
amount of time possible. In this paper, we derive a set of formal parameters,
based on mathematical functions, for comparing knowledge elicitation
techniques. We use the landscape study task (a sub-task of environmental
planning) as an illustrating example throughout.
1 Introduction
Although, in the past decade, several methodologies for Knowledge Acquisition
(KA) have been developed, the knowledge elicitation process is still more an
art than a science. There are many different elicitation techniques (Cooke,
1994) and selecting the "right" technique in a particular situation is not
trivial. Moreover, knowledge elicitation involves skilled people and this makes
it an important cost-determining factor in the development process of a
knowledge-based system (KBS). There are two important factors to consider here:
(1) the kind of knowledge the technique elicits and (2) the time needed to
apply the technique. In a particular knowledge engineering situation, one
would, ideally, use an elicitation technique that provides all the relevant
knowledge in the minimum amount of time possible.
Previous work has shown that there exists a relationship between, on the one
hand, the elicitation technique used to gather data and, on the other hand, the
resulting model of expert knowledge (Nisbett and Wilson, 1977; Berry, 1987;
Gammack, 1992). This implies that we should not economise by opting for a
cheaper technique if this technique cannot elicit the relevant knowledge.
However, we can optimise the elicitation process by trying to minimise the time
spent on the elicitation process. Previous work on knowledge elicitation
techniques has focused on empirical comparisons (Burton, Shadbolt, Rugg, and
Hedgecock, 1990).
The aim of this paper is to formally characterise elicitation techniques
concerning the required time of their application in relation to a quantitative
measure of the knowledge they provide. The aim is achieved by deriving a set of
formal parameters for comparing elicitation techniques, based on a
normalisation of the underlying knowledge. The ideas in the paper are
developed, based on, and will be illustrated with an existing KBS project for
environmental planning in Spain.
In the overall development process of a KBS, this work has to be situated in
the first stage, namely in the knowledge elicitation phase. Modern knowledge
acquisition methodologies such as KADS (Wielinga, Schreiber, and Breuker,
1992), VITAL (O'Hara, Motta, and Shadbolt, 1994) and PROTÉGÉ
(Puerta, Egar, Tu, and Musen, 1992) are concerned with conceptual modelling
(based on the elicited knowledge) and with later stages in the KBS development
process. Therefore, the result of our work can be of use for each of these
methodologies.
The structure of the paper is as follows. Section 2 offers a brief overview of
the main factors which influence the duration of knowledge elicitation
processes. Also, assumptions to be taken into account in the rest of the paper
in relation to these factors are put forward. In Section 3, we formally
describe characteristics of elicited knowledge by means of mathematical
funstions, and we introduce an algorithm for sampling the amount of knowledge.
In Section 4, we present a design of parameters for comparing knowledge
elicitation techniques with respect to their respective knowledge samples
obtained after applying the mentioned algorithm. Section 5 shows an example
where the theory introduced in the previous sections is used to compare the
structured interview method with the unstructured one for an assessment
problem. Finally, in Section 6 we present conclusions.
2 The Elicitation-Process Handicap
One of the reasons that it is expensive to develop KBSs, is that the
development process involves considerable time and effort of knowledge
engineers and domain experts, and such people are costly. In this sense, the
knowledge elicitation process (KEP) is an important cost-determining factor in
the whole knowledge acquisition process. This is one of the reasons that some
researchers try to do the job without knowledge engineers. For example, Ripple
Down Rules (Kang, Compton, and Preston, 1995) allow to perform knowledge
acquisition without knowledge engineers; human experts directly input the rules
which are relevant to solve the problem (although at the expense of the
structure of the rule base). Other research groups focus on automatic
generation of elicitation tools in which the domain experts can directly put
their knowledge. Examples include SALT and MOLE (Marcus, 1988),
PROTÉGÉ (Puerta, Egar, Tu, and Musen, 1992), and DIDS (Runkel and
Birmingham, 1993).
However, in many situations, interaction between a knowledge engineer and
domain expert remains indispensable. In order to keep the costs as low as
possible, we want to minimise the time of the KEP, while keeping its content.
We hope to achieve this goal by selecting the adequate elicitation technique in
different situations. To do that, first, we have to identify the possible
causes of the duration of the KEP. Hart (1986) and Cooke (1994), identify a
number of them, which we briefly review in the following paragraphs.
The number of experts Some problems require several experts in different
areas. For example, the environmental planning task requires knowledge of
geology, zoology, botanical, ecology, economy, hydrology, and forestry
engineering. It is not likely to find all these skills in one person, but in
several experts. This implies that each of the experts will have a particular,
probably distinct, language for describing his or her domain.
As a consequence of this variety of languages, redundancies and inconsistencies
can be introduced and, hence, it will increase the duration of the KEP. For
example, consider that there are two experts who participate in the
environmental planning project whose objective is to evaluate the visual
fragility[1] of a landscape belonging to a
particular forest. Let us assume that one of the experts is a zoologist (Z)
and the other a botanist (B). Suppose that expert Z states that "if the diet of
the rabbits of the forest is constituted by singular plants then the visual
fragility of the forest is high", while expert B asserts that "if there are
rare plants, the fragility of the forest could be high". After having analysed
the respective antecedents of the above assertions, it may arise that the verbs
to constitute and to exist are synonyms, as well as the concepts
rare plants and singular plants.
The domain In some domains, the elicited knowledge may become invalid
before it has been made operative in a KBS. This occurs for example when the
basis of the theory supporting the principles of expert actions changes during
the development process. In the environmental planning project, this could
happen when the corresponding policy of the government changes during the KEP
(e.g., because of a change of president).
Other domain related factors that complicate the KEP include: (1) the needed
knowledge is strictly confidential (e.g., for strategic reasons); (2) the
knowledge required to solve the problem is expensive to obtain (e.g., because
experts are not readily available due to long travel distances); (3) the
knowledge may be complex (e.g., because the experts reason with uncertainty and
with linguistic hedges (Hwang, 1995)) such as very, high,
more, etc.
The knowledge engineer The knowledge engineer, as a person with certain
characteristics, is also an important factor for the time needed for the KEP.
Welbank (1983) identifies a number of interpersonal skills which a knowledge
engineer ideally should possess, including self-confidence, tact and diplomacy,
and intelligence; versatility and inventiveness; empathy, patience and
persistence. Moreover, a knowledge engineer has to know about domain and
programming knowledge, and about elicitation techniques, machine learning
techniques, expertise modelling, knowledge representation methodologies and
available commercial shells.
The context The context relates to the equipment (e.g. tape recorder,
video) used for interviewing the experts, the environmental characteristics of
the location where the KEP occurs, etc. For example, if a knowledge engineer
does not have a tape recorder or a video recorder at his or her disposal, and
interviews have to be taken, it will take more time to record experts' answers
in general.
2.1 Assumptions
With respect to the KEP, and taking into account the just mentioned factors, in
the rest of the paper we make the following assumptions in order to keep our
problem manageable.
Assumption 1 The kind of problems to be solved concern domains in which
knowledge of different areas is needed. We assume that these domains may be
structured in such a way that each area corresponds to a separate task as
distinguished in the KADS methodology (Wielinga, et al., 1992). Thus, we assume
an interdisciplinary problem, where each individual discipline involves a
separate task.
Assumption 2 There are Ne available experts, Ne
> 1, in such a way that they cover all the disciplines underlying the tasks
whose expert knowledge needs to be elicited. Moreover, there is at least one
expert per involved discipline. In addition, we will assume Ne is
constant during the KEP. It is clear that using the same human expert for a
specific task during the entire KEP facilitates consistency among the segments
of knowledge obtained with elicitation techniques. We also assume that experts
are available whenever they are needed during the KEP.
Assumption 3. Because we aim at comparing knowledge elicitation
techniques, we assume that all known techniques from the literature, as well as
the equipment necessary to carry out each of such techniques, are available.
Moreover, we assume that the knowledge engineer knows how to apply each
elicitation technique.
Assumption 4 Most knowledge elicitation techniques require the active
participation of elicitors. Analogue to keeping the same human experts
during the KEP, we assume the same elicitor during the KEP.
Assumption 5 Each knowledge elicitation session is carried out in such a
way that the addition of knowledge during a knowledge elicitation session does
not invalidate knowledge elicited in previous sessions.
A problem that satisfies the assumptions mentioned above is referred to as a
knowledge engineering solvable problem (KE-solvable
problem).
In this paper, we are interested in a comparison of knowledge elicitation
techniques, which is needed to address questions such as the validity of the
techniques (Cooke, 1994). Mathematical analysis provides a rigorous "corpus" to
perform such comparison in a formal and systematic way. It can be used to model
the process of extracting concepts and relations after each elicitation
session. In particular, several functions for quantifying concepts, their
attributes and their values can be defined by using mathematical analysis. In
the following, we will present a formal framework, built on top of the
mentioned assumptions, to derive parameters which can be used to compare
knowledge elicitation techniques.
3 Accumulation and Finiteness of the Elicited Knowledge
We focus on expert knowledge for solving a KE-solvable problem from a
quantitative point of view. More precisely, we are interested in the time spent
on eliciting knowledge from human experts and in representing this knowledge in
countable entities. The definitions in the following subsection aim at
defining, in a step-by-step process, the knowledge function which is the base
for deriving the formal parameters later in the paper.
3.1 Knowledge functions
Definition 1: ASS Let Kru be the set of possible decision
rules[2] which can be elicited from human
experts, and let Kc be the set of semantically different
concepts[3] underlying
Kru. The Association operator, written ASS, is defined as a
function which maps Kru to Kc in order to obtain the
semantically different concepts underlying a particular decision rule elicited
from some expert.
Definition 2: ISA Given a hierarchy of concepts elicited earlier, the
Ascendants, operator, written ISA, is defined as a function which maps
Kc to itself in order to obtain the set of ascendant concepts of a
concept obtained after applying the ASS operator to a particular decision rule
elicited from one or more experts.
Definition 3: PRO Let Kp be the set of properties relative to
Kc. The Properties operator, written PRO, is defined as a
function which maps the Cartesian product Kru x Kc to
Kp in order to obtain for each concept the set of properties
involved in a particular rule from which that concept has been obtained (i.e.,
after applying the ASS operator to the rule under question). For example, by
assuming that r is a decision rule elicited from one or more experts, and z is
a concept belonging to ASS(r), PRO (r, z) provides the set of properties, which
have to do with z, implicitly or explicitly referenced in r. In order to solve
possible ambiguity problems, each of the so obtained properties can be written
as concept.property, where property = PRO (r, z) and
concept = z.
Definition 4: VAL Let Kv be the set of possible values
associated to the elements of Kc. The Values operator,
written VAL, is defined as a function which maps the Cartesian product
Kru x Kc x Kp to Kv. For
instance, by assuming that r is a decision rule elicited from one or more
experts, that the concept z  ASS(r), and that the property u
ASS(r), and that the property u
 PRO(r,z), VAL(r,z,u) provides the value corresponding to the
concept z for the property u in such a way that it can explicitly be extracted
from r. Possible ambiguity problems can be solved by introducing the notation
concept.property.value, where value is equal to VAL(r,z,u);
property is the property referenced by value, that is, u;
concept is the concept to which value is linked, that is,
z.
PRO(r,z), VAL(r,z,u) provides the value corresponding to the
concept z for the property u in such a way that it can explicitly be extracted
from r. Possible ambiguity problems can be solved by introducing the notation
concept.property.value, where value is equal to VAL(r,z,u);
property is the property referenced by value, that is, u;
concept is the concept to which value is linked, that is,
z.
Due to the way ASS, ISA, PRO and VAL are defined above, their arguments can
only consist of single elements, and not of sets of elements. However,
sometimes it may be necessary that the functions accept a set of elements as
arguments. For example, when dealing with sets of rules or concepts as a whole.
In the following, we will extend the definitions in such a way that their
arguments can manage sets of elements.
Definition 5: MASS Let R be a non-empty set of expert decision rules.
The multiple association operator, written MASS, is defined as
follows:
 ,
where rj stands for the jth rule belonging to R, j =
1,..,Card(R).
,
where rj stands for the jth rule belonging to R, j =
1,..,Card(R).
In a analogous way, we can extend the function of ISA.
Definition 6: MISA Let R be a non-empty set of expert decision rules,
and let C be equal to MASS(R). The multiple ascendants operator, written
MISA, is defined as
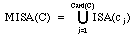 ,
where cj
stands for the ith concept belonging to C, j = 1,..,Card(C).
,
where cj
stands for the ith concept belonging to C, j = 1,..,Card(C).
Similarly, we can do the same for PRO. However, for readability reasons, we
will do it in a two-step process.
Definition 7: MPRO Let r be an expert decision rule, such that C =
ASS(r). The multiple properties operator, written MPRO, is defined as
follows:
 ,
where ck stands for the kth element belonging to C, k =
1,..,Card(C).
,
where ck stands for the kth element belonging to C, k =
1,..,Card(C).
Definition 8: EPRO Let R be a non-empty set of expert decision rules,
and C be equal to MASS(R). The extended property operator, written EPRO,
is defined as follows:
 ,
where Cj = ASS (rj), j = 1,..,Card(R).
,
where Cj = ASS (rj), j = 1,..,Card(R).
By proceeding in a similar way as done for the PRO operator, we can extend the
definition for VAL.
Definition 9: MPVAL Let r be an expert decision rule, and let c be a
concept belonging to ASS(r) such that P = PRO(r,c). The multiple properties
value operator, written MPVAL, is defined as follows:
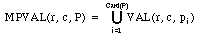 ,
where pi stands for the ith element belonging to P, i = 1, 2, ...,
Card(P).
,
where pi stands for the ith element belonging to P, i = 1, 2, ...,
Card(P).
Definition 10: MCVAL Let r be an expert decision rule, and let C be
equal to ASS(r) such that P = MPRO(r, C). The multiple concepts value
operator, written MCVAL, is defined as follows:
 ,
where i stands for the ith element belonging to C, i = 1, 2, ..., Card(C).
,
where i stands for the ith element belonging to C, i = 1, 2, ..., Card(C).
Definition 11: EVAL Let R be a non-empty set of expert decision rules,
let C be equal to MASS(R) and let P be equal to EPRO(R, C). The extended
assessment operator, written EVAL, is defined as follows:
 ,
where ri stands for the ith element belonging to R, i = 1, 2, ...,
Card(R).
,
where ri stands for the ith element belonging to R, i = 1, 2, ...,
Card(R).
Definition 12: K*(t) Let Kru(t) be the set of
decision rules which have been elicited from one or more human experts until
the instant t, let Kc(t) be MASS(Kru(t)), and let
Kr(t) be equal to the union set MISA(Kc(t))  EPRO(Kru(t), Kc(t))
EPRO(Kru(t), Kc(t))  EVAL(Kru(t),
Kc(t), EPRO(Kru(t), Kc(t))). Using the above
terminology, the amount Card(Kc(t)) + Card(Kr(t)),
written K*(t), is said to be the cumulative knowledge function
until t.
EVAL(Kru(t),
Kc(t), EPRO(Kru(t), Kc(t))). Using the above
terminology, the amount Card(Kc(t)) + Card(Kr(t)),
written K*(t), is said to be the cumulative knowledge function
until t.
As immediate consequences, the next properties with respect to K*(t)
can be established:
1. K*(t) >= 0.
Proof Only two possible situations can arise:
a) t = 0. Before the KEP begins, there is no elicited knowledge and, hence,
K*(0) = 0.
b) t > 0. In that case:
K*(t) =

2. K*(t) is an increasing, monotonous function.
Proof It is obvious that as more time is consumed by the KEP, the amount
of elicited knowledge either increases or remains as a constant, but never
decreases.
3.2 Example
Suppose that the following information elicited until ti is
available: Kru(ti) = {"If the vegetation is very low,
there is only one stratum and the seasonal_variation is medium, then the area
under study has got a low visual fragility", "If there exists a
predominance of pine merged with stone outcrops then the area under study has
got a high visual quality"} = {R1, R2}. At this point, we can obtain
K*( ti) through the following step-by-step process:
1. By applying the ASS function to R1 and R2 respectively, we get:
ASS(R1) = {vegetation, visual fragility}, ASS(R2) = {pine, visual quality} .
2. Based in this, we can calculate MASS(Kru(ti)) as
follows:
MASS(Kru(ti)) = MASS({R1, R2}) = ASS(R1)  ASS(R2)
= {vegetation, visual fragility, pine, visual quality}.
ASS(R2)
= {vegetation, visual fragility, pine, visual quality}.
So, Card(MASS(Kru(ti))) = 4.
3. The ISA function is applied to each of the elements of
MASS(Kru(ti)):
ISA(vegetation) = {vegetation_uses};
ISA(visual_fragility) = {visual_parameter };
ISA(pine) = {tree, vegetation, vegetation_uses};
ISA(visual_quality) = {visual_parameter };
4. By considering steps 2 and 3, MISA(MASS(Kru(ti))) =
MISA({vegetation, visual_fragility, pine, visual_quality}) = ISA(vegetation)
 ISA(visual_fragility)
ISA(visual_fragility)  ISA(pine)
ISA(pine)  ISA(visual_quality) =
{tree, vegetation, vegetation_uses, visual_parameter}.
ISA(visual_quality) =
{tree, vegetation, vegetation_uses, visual_parameter}.
So, Card(MISA(MASS(Kru(ti)))) = 4.
5. Then, the PRO operator is applied to each decision rule:
PRO(R1, vegetation)={height, number_of_strata, seasonal_variation};
PRO(R1, visual_fragility) = {assessment};
PRO(R2, pine) = { merging_with_stone_outcrops, predominance};
PRO(R2, visual_quality) = { assessment};
6. By taking into account step 5, it is easy to obtain the following:
MPRO(R1, ASS(R1)) = MPRO(R1, {vegetation, visual_fragility}) = PRO(R1,
vegetation) PRO(R1,visual_fragility)={vegetation.height,vegetation.number_of_strata,vegetation.seasonal_variation,visual_fragility.assessment};
PRO(R1,visual_fragility)={vegetation.height,vegetation.number_of_strata,vegetation.seasonal_variation,visual_fragility.assessment};
MPRO(R2, ASS(R2)) = MPRO(R2, {pine, visual_quality}) = PRO(R2,pine)  PRO(R2,visual_quality)={pine.merging_with_stone_outcrops,pine.predominance,visual_quality.assessment}.
PRO(R2,visual_quality)={pine.merging_with_stone_outcrops,pine.predominance,visual_quality.assessment}.
7. By using the results of step 6, the EPRO functions can be written as
follows:
EPRO(Kru(ti), MASS(Kru(ti))) =
MPRO(R1, ASS(R1))  MPRO(R2, ASS(R2)) =
{vegetation.height,vegetation.number_of_strata,vegetation.seasonal_variation,pine.merging_with_stone_outcrops,pine.predominance,visual_fragility.assessment,visual_quality.assessment
}.
MPRO(R2, ASS(R2)) =
{vegetation.height,vegetation.number_of_strata,vegetation.seasonal_variation,pine.merging_with_stone_outcrops,pine.predominance,visual_fragility.assessment,visual_quality.assessment
}.
So, Card(EPRO(Kru(ti),
MASS(Kru(ti)))) = 7
8. If the VAL function is now applied to the results obtained for the moment,
we get the following:
VAL(R1, vegetation, height) = {very_low};
VAL(R1, vegetation, number_of_strata) = {1};
VAL(R1, vegetation, seasonal_variation) = {medium};
VAL(R1, visual_fragility, assessment) = {low};
VAL(R2, pine, merging_with_stone_outcrops) = {true};
VAL(R2, pine, predominance) = {true};
VAL(R2, visual_quality, assessment) = {high}.
9. By applying the MPVAL definition, the following can be obtained:
MPVAL(R1, vegetation, PRO(R1, vegetation)) = VAL(R1, vegetation,
height) AL(R1,vegetation,number_of_strata)
AL(R1,vegetation,number_of_strata) VAL(R1,vegetation,seasonal_variation)={height.very_low,number_of_strata.1,
Vseasonal_variation.medium}
VAL(R1,vegetation,seasonal_variation)={height.very_low,number_of_strata.1,
Vseasonal_variation.medium}
MPVAL(R1,visual_fragility, PRO(R1, visual_fragility)) = VAL(R1,
visual_fragility, assessment) = {low}
MPVAL(R2, pine, PRO(R2,pine)) = VAL(R2, pine, merging_with_stone_outcrops)
 VAL(R2, pine, predominance) = { merging_with_stone_outcrops.true,
predominance.true}
VAL(R2, pine, predominance) = { merging_with_stone_outcrops.true,
predominance.true}
MPVAL(R2,visual_quality, PRO(R2, visual_quality)) = VAL(R2, visual_quality,
assessment) = {high}
10. If the MCVAL definition is applied, the next formulae can be written:
MCVAL(R1, ASS(R1), MPRO(R1, ASS(R1)))) = MPVAL((R1, vegetation,
PRO(R1,vegetation))  MPVAL(R1,visual_quality, PRO(R1,visual_fragility))
=
{vegetation.height.very_low,vegetation.number_of_strata.1,vegetation.seasonal_variation.medium,visual_fragility.assessment.low}
MPVAL(R1,visual_quality, PRO(R1,visual_fragility))
=
{vegetation.height.very_low,vegetation.number_of_strata.1,vegetation.seasonal_variation.medium,visual_fragility.assessment.low}
MCVAL(R2, ASS(R2), MPRO(R2, ASS(R2)))) = MPVAL((R2, pine, PRO(R2, pine))
 MPVAL(R2,visual_quality,PRO(R2,visual_quality))={pine.merging_with_stone_outcrops.true,pine.predominance.true,visual_quality.assessment.high}
MPVAL(R2,visual_quality,PRO(R2,visual_quality))={pine.merging_with_stone_outcrops.true,pine.predominance.true,visual_quality.assessment.high}
11. After that, EVAL definition can be applied to step 10 as follows:
EVAL(Kru(ti), MASS(Kru(ti)),
EPRO(Kru(ti), MASS(Kru(ti)))) =
MCVAL(R1, ASS(R1), MPRO(R1, ASS(R1))))  MCVAL(R2, ASS(R2), MPRO(R2,
ASS(R2)))) =
{vegetation.height.very_low,vegetation.number_of_strata.1,vegetation.seasonal_variation.medium,visual_fragility.assessment.low,pine.merging_with_stone_outcrops.true,pine.predominance.true,visual_quality.assessment.high}
MCVAL(R2, ASS(R2), MPRO(R2,
ASS(R2)))) =
{vegetation.height.very_low,vegetation.number_of_strata.1,vegetation.seasonal_variation.medium,visual_fragility.assessment.low,pine.merging_with_stone_outcrops.true,pine.predominance.true,visual_quality.assessment.high}
Finally, if definition 12 is applied, K*(ti)=
Card(MASS(Kru(ti))) + (MISA(Kc(t))
 EPRO(Kru(ti), Kc(ti))
EPRO(Kru(ti), Kc(ti))
 EVAL(Kru(ti), Kc(ti),
EPRO(Kru(ti), Kc(ti)))) = 4 + 4 + 7
+ 7 = 22
EVAL(Kru(ti), Kc(ti),
EPRO(Kru(ti), Kc(ti)))) = 4 + 4 + 7
+ 7 = 22
Once the KEP has begun, it may be useful to know the proportion of concepts
with respect to the total of knowledge which has been elicited until an
instant. That proportion is formally defined as follows:
Definition 13: [rho]c(t) Let Kru(t) be the set of
decision rules which have been elicited from experts until the instant t, let
Kc(t) be MASS(Kru(t)), and let Kr(t) be equal
to MISA(Kc(t))  EPRO(Kru(t), Kc(t))
EPRO(Kru(t), Kc(t))
 EVAL(Kru(t), Kc(t), EPRO(Kru(t),
Kc(t))). The density of concept knowledge elicited until t,
written [rho]c(t), is defined as the quotient
[rho]c(t) =
EVAL(Kru(t), Kc(t), EPRO(Kru(t),
Kc(t))). The density of concept knowledge elicited until t,
written [rho]c(t), is defined as the quotient
[rho]c(t) =
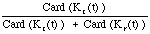 .
.
In the same way, we can define a parameter which denotes information about the
proportion of knowledge involving characteristics of concepts and relationships
among them, with respect to the total amount of knowledge which has been
elicited until an instant.
Definition 14: 1 - [rho]c(t). Let [rho]c(t)
the density of concept knowledge elicited until t.The density of non-concept
knowledge elicited until t, written [rho]nc(t), is defined as
the difference 1 - [rho]c(t).
So far, there is no guarantee of finiteness of the knowledge. Infiniteness of
knowledge would mean that the amount of knowledge continues to increase. In
practical knowledge elicitation settings it is, however, reasonable to assume
that there exist a finite amount of knowledge needed to solve a particular
KE-solvable problem. The next definition introduces the concept of finiteness
for the KEP.
Definition 15: finite, cumulative knowledge function Let
K*(t) be a cumulative knowledge function until t. K*(t)
is said to be a finite, cumulative knowledge function, written
Kf*(t), if there exists a finite instant te,
called time of elicitation, such that the following equality holds:
Kf*(t) = Kf*(te) for all
t >= te.
Considering what has been pointed out so far, we can establish some results by
means of the following corollaries:
Corollary 1
Let Kf*(t) be a finite, cumulative knowledge function
until the instant t, and let te be the time of elicitation for
Kf*(t). Then, Kf*(t) can be written
as follows:
Kf*(t) =

where ti denotes the instant at which the ith sample of
Kf*(t) has been taken, i = 1, 2, ..., e; and
{Kf*(ti)}ni stands for the set
composed by ni times the element
Kf*(ti) such that:
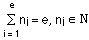 .
.
Corollary 2
Let Kf*(t) be a finite, cumulative knowledge function
until the instant t, and let te be the time of elicitation for
Kf*(t).Then, the function Kf*(t)
has e points at most, where Kf*(t) is non-continuous,
where e corresponds to the sample of Kf*(t) at which
te has been reached.
Proof It is obvious if we take into account that
Kf*(tj) >=
Kf*(ti), 1 <= i < j <= e.
3.3 The Knowledge Functions Calculation (KFC) Algorithm
In the previous section, we have established, in a step-by-step process,
a mathematical knowledge function to characterise the existence of a finite
instant at which the knowledge necessary to solve a particular KE-solvable
problem (P) is reached. Based on this we are able to describe a very simple
algorithm to find out the value of te and, hence, of
Kf*(te).
Let En be a non-empty set of experts who participate in a KEP[4], and let KAT be a function standing for the
available knowledge analysis techniques to be applied to the elicited expert
knowledge (i.e., to be applied to its argument) required to solve P. The KFC
algorithm can be written as follows:
KFC(En, KAT, operative_knowledge, te)
begin
sample_number = 0;
repeat
sample_number = sample_number + 1;
current_knowledge = KAT (Kc(tsample_number)  Kr(tsample_number));
until validation(current_knowledge, En);
te = tsample_number;
operative_knowledge = Kf*(te)
end
Kr(tsample_number));
until validation(current_knowledge, En);
te = tsample_number;
operative_knowledge = Kf*(te)
end
where validation is a Boolean function which returns true if the set of
all available experts (Nexp) validates a knowledge base
(current_KB). More precisely:
validation(current_KB, Nexp)
begin
expert_number = 0
status = OK;
repeat
expert_number = expert_number + 1;
status = check(current_KB, expert_number)
until (expert_number = Nexp + 1) or status = false;
end;
return status
where the function check can be defined as follows:
check =
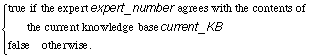
4 Deriving Formal Parameters to Compare Knowledge Elicitation Techniques
In this section, we use the mathematical results obtained to derive relevant
parameters for comparing knowledge elicitation techniques for solving
KE-solvable problems.
Parameter 1: delay factor Let tei and
tej be the times of elicitation corresponding to two
finite, cumulative knowledge functions obtained after applying two knowledge
elicitation techniques Mi and Mj respectively for solving
a KE-solvable problem, written P. Mi is said to delay the KE process
for solving P less (more) than Mj does if tei
< (>) tej. The technique with the smallest delay
factor is the preferred one.
Parameter 2: complexity of the technique We can also consider the amount
of knowledge corresponding to the time of elicitation obtained after applying
each of the available elicitation techniques. Thus, the number of concepts and
relationships affecting them, obtained after using a particular knowledge
elicitation technique, have an influence on what can be entailed from it
(Lehmann and Magidor, 1992) as well as on the presence of inconsistencies
(Goldszmidt and Pearl, 1991) within that knowledge.
Let Kfi*(t) and Kfj*(t) be two
finite, cumulative knowledge functions obtained after applying two different
knowledge elicitation techniques Mi and Mj, respectively
to solve a KE-solvable problem P; and let tei and
tej be the times of elicitation corresponding to each of
those functions. Mi is said to introduce more (less) complexity into
the KE process than Mj does if Kfi*(
tei) >(<) Kfj*(
tej). The above definition, however, only takes into
account the final value of Kf*(t) in order to evaluate the
complexity associated to a particular knowledge elicitation methodology.
We can also separately consider the complexity related to the number of
concepts, and to the amount of knowledge referring to the concepts (i.e.,
characteristics and taxonomic relationships involving concepts earlier
elicited). This is the motivation for the following two definitions:
Parameter 3: concept complexity of the technique Let
[rho]ci and [rho]cj be the average
density of elicited concept knowledge obtained after applying the knowledge
elicitation methodologies Mi and Mj ,respectively, to the
same problem. Mi is said to be more (less) concept complex
than Mj is if [rho]ci >(<)
[rho]cj.
Parameter 4: non-concept complexity of the technique Let
[rho]nci and [rho]ncj be the
density of elicited non-concept knowledge elicited obtained after applying the
knowledge elicitation methodologies Mi and Mj,
respectively, to the same problem. Mi is said to be more (less)
non-concept complex than Mj is if
[rho]nci >(<) [rho]ncj.
By making an analogy with physics, a number of additional parameters can be
derived.
Parameter 5: speedup Let Kf*(t) be a finite,
cumulative knowledge function until the instant t. Then, the speedup of
knowledge elicitation at t, written SE(t), can be defined as follows:
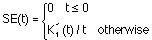
Parameter 6: acceleration Let SE(t) be the speedup of the knowledge
elicitation at the instant t. Then, the acceleration of the knowledge
elicitation at the instant t, written AE(t), can be defined as:
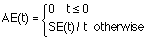
Parameter 7: sleeping time Another perspective of the KEP is to consider
the period of time in which there is no gain of relevant knowledge for solving
the KE-solvable problem under consideration. Let Kf*(t)
be a finite, cumulative knowledge function until the instant t, and let
te be the time of elicitation for Kf*(t).
Then, the sleeping time for Kf*(t), written
St, is defined as follows:
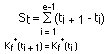
Parameter 8: effective elicitation time By using the above parameter, we
can determine the effective time of knowledge elicitation, that is, the period
in which there has been a continuous gain of knowledge, relevant for solving a
certain problem[5]. Let
Kf*(t) be a finite, cumulative knowledge function until
the instant t, te the time of elicitation for
Kf*(t) and St the sleeping time for
Kf*(t). Then, the time of effective elicitation
for Kf*(t), written EET, is defined as the
difference te - St.
Parameter 9: laziness/activeness Let Kfi*(t) and
Kfj*(t) be two finite, cumulative knowledge functions
obtained after applying two different knowledge elicitation techniques
Mi and Mj, respectively to solve a KE-solvable problem P;
and let EETi and EETj be the respective times of
effective elicitation corresponding to these functions. Then,
Mi is said to be lazier than Mj is if EETi
< EETj. In a similar way, Mi is said to be
more active than Mj is if EETi <
EETj.
Parameter 10: relative time of effective elicitation Elaborating on the
previous parameter, we can consider the time of effective elicitation compared
to the total elicitation time of each technique. Let
Kf*(t) be a finite, cumulative knowledge function until
the instant t, te the time of elicitation for
Kf*(t) and EET the elicitation effective time for
Kf*(t). Then, the relative time of effective
elicitation for Kf*(t), written REET, is defined as
the quotient EET/te.
Parameter 11: relative laziness/activeness If we consider the previous
definition, another parameter for comparing knowledge elicitation techniques
can be derived. Let REETi and REETj be the relative times
of effective elicitation corresponding to two knowledge elicitation
techniques Mi and Mj respectively. Mi is said
to be relatively lazier than Mj if REETi <
REETj.
5 An Example: The Landscape Study.
In this section, we present the problem for which we have performed the
knowledge elicitation process. The problem is known as a natural resources
planning task and the project has been carried out in co-operation with the
Spanish Council for Scientific Research (CSIC). Nowadays, natural
resources planning studies become more and more important, at least in the
western world. To accomplish this kind of studies, AI techniques are gaining
popularity in the environmental planning community. So far, several KBSs and
expert systems prototypes have been developed (Starfield and Bleloch, 1983;
Hunt, Middleton, Grime, and Hodgson, 1991; Martinez-Bejar, Castillo, and
Martin, 1995).
Natural resources planning embodies a sub-task called physical media study
which consists of performing a number of tasks, including the risks study,
the fauna study, the vegetation study, the geology study, the water resources
study, and the landscape study, given a particular geographic area under study
(called polygon). In its turn, the polygon is usually divided into
units.
Each sub-task belonging to the physical media study may be characterised as a
polygonal-units assessment task, that is, as a polygonal-units classification
task (Wielinga, Schreiber, and Breuker, 1992). This task is carried out by
means of certain descriptive variables whose nature depends on each sub-task.
Thus, the objective of the landscape study task is to make an assessment of
each of the landscape units in the polygon from a landscape point of view. The
assessment is typically performed by means of the following two parameters,
which need to be found for each of the landscape units:
Visual Quality (VQ) of a landscape is defined as the beauty grade
from the vegetation-uses, the geology-geomorphology, and the hydrology points
of view simultaneously.
Visual Fragility (VF) of a landscape refers to its sensitivity to
changes caused by human activities.
Basically, the goal of the landscape study task[6] consists of obtaining a binomy B = (VQ, VF) for each
landscape unit in the polygon under study. Figure 1 shows a polygon composed of
7 units assessed from the landscape point of view. The natural numbers into
brackets represent the values for VQ and VF, respectively.
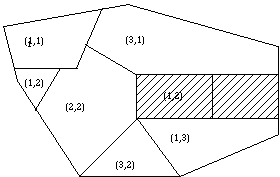
FIGURE 1 - A polygonal area showing the results of performing
the landscape study task
5.1 Landscape study: a KE-solvable problem?
In order to apply the results obtained in this paper, we need to ensure that
the landscape study task is a KE-solvable problem. In other words, we need to
ensure that the assumptions (see Section 2) hold.
Assumption 1 The problem (P) to be solved consists of determining both
the visual quality and the visual fragility of a landscape. It implies to
assess both parameters for a particular landscape from different point of
views, including vegetation-uses, water resources, and geology-geomorphology.
Each point of view is considered as a separate task. So, assumption 1 is
satisfied.
Assumption 2 There have been 10 experts available to elicit the
knowledge required to solve P, which is in accordance with assumption 2.
Assumption 3 In the landscape project, we have restricted the `world' of
elicitation techniques to two of them: the structured interview and the
unstructured interview. So, assumption 3 also holds.
Assumption 4 The elicitor has been the same person during the whole KEP.
So, assumption 4 is satisfied as well.
Assumption 5 Prior to each elicitation session, the experts were given a
manuscript containing the knowledge elicited until that moment in order to
ensure that the elicitation session to be performed did not invalidate the
knowledge obtained so far. In addition, after each elicitation session, the
experts validated the knowledge elicited with respect to the previous
elicitation sessions. In this way, assumption 5 is also true.
Thus, we can conclude that P is KE-solvable.
5.2 Applying the KFC algorithm
In this section, we apply the KFC algorithm to solve P. As mentioned before,
there are two candidate elicitation techniques to be tested in the context of
solving P. After applying the KFC algorithm to each of them, the next tables
were obtained:
t
|
Card(Kc(t))
|
Card(Kr(t))
|
pc(t)
|
pnc(t)
|
K*(t)
|
SE(t)
|
AE(t)
|
|
|
|
|
|
|
|
|
15
|
8
|
14
|
0.363636364
|
0.636363
|
22
|
1.466666
|
0.097777
|
30
|
10
|
18
|
0.357142857
|
0.642857
|
28
|
0.933333
|
0.031111
|
45
|
10
|
24
|
0.294117647
|
0.705882
|
34
|
0.755555
|
0.016790
|
60
|
13
|
28
|
0.317073171
|
0.682926
|
41
|
0.683333
|
0.011388
|
75
|
13
|
31
|
0.295454545
|
0.704545
|
44
|
0.586666
|
0.007822
|
90
|
19
|
39
|
0.327586207
|
0.672413
|
58
|
0.644444
|
0.007160
|
105
|
21
|
47
|
0.308823529
|
0.691176
|
68
|
0.647619
|
0.006167
|
120
|
24
|
51
|
0.32
|
0.68
|
75
|
0.625
|
0.005208
|
135
|
25
|
59
|
0.297619048
|
0.702380
|
84
|
0.622222
|
0.004609
|
150
|
27
|
65
|
0.293478261
|
0.706521
|
92
|
0.613333
|
0.004088
|
165
|
31
|
79
|
0.281818182
|
0.718181
|
110
|
0.666666
|
0.004040
|
180
|
32
|
92
|
0.258064516
|
0.741935
|
124
|
0.688888
|
0.003827
|
195
|
32
|
101
|
0.240601504
|
0.759398
|
133
|
0.682051
|
0.003497
|
210
|
32
|
106
|
0.231884058
|
0.768115
|
138
|
0.657142
|
0.003129
|
225
|
32
|
106
|
0.231884058
|
0.768115
|
138
|
0.613333
|
0.002725
|
240
|
33
|
110
|
0.230769231
|
0.769230
|
143
|
0.595833
|
0.002482
|
255
|
33
|
112
|
0.227586207
|
0.772413
|
145
|
0.568627
|
0.002229
|
270
|
33
|
112
|
0.227586207
|
0.772413
|
145
|
0.537037
|
0.001989
|
285
|
38
|
135
|
0.219653179
|
0.780346
|
173
|
0.607017
|
0.002129
|
300
|
40
|
154
|
0.206185567
|
0.793814
|
194
|
0.646666
|
0.002155
|
315
|
41
|
165
|
0.199029126
|
0.800970
|
206
|
0.653968
|
0.002076
|
330
|
47
|
190
|
0.198312236
|
0.801687
|
237
|
0.718181
|
0.002176
|
345
|
49
|
199
|
0.197580645
|
0.802419
|
248
|
0.718840
|
0.002083
|
360
|
50
|
201
|
0.199203187
|
0.800796
|
251
|
0.697222
|
0.001936
|
375
|
51
|
209
|
0.196153846
|
0.803846
|
260
|
0.693333
|
0.001848
|
390
|
51
|
217
|
0.190298507
|
0.809701
|
268
|
0.687179
|
0.001761
|
405
|
51
|
220
|
0.188191882
|
0.811808
|
271
|
0.669135
|
0.001652
|
20
|
52
|
223
|
0.189090909
|
0.810909
|
275
|
0.654761
|
0.001558
|
435
|
52
|
225
|
0.187725632
|
0.812274
|
277
|
0.636781
|
0.001463
|
450
|
52
|
228
|
0.185714286
|
0.814285
|
280
|
0.622222
|
0.001382
|
Table 1. The value of some parameters for the structured interview
method (M1).
t
|
Card(Kc(t))
|
Card(Kr(t))
|
pc(t)
|
pnc(t)
|
K*(t)
|
SE(t)
|
AE(t)
|
|
|
|
|
|
|
|
|
15
|
3
|
9
|
0.25
|
0.75
|
12
|
0.8
|
0.053333
|
30
|
7
|
15
|
0.318181818
|
0.681818
|
22
|
0.733333
|
0.024444
|
45
|
9
|
17
|
0.346153846
|
0.653846
|
26
|
0.577777
|
0.012839
|
60
|
10
|
20
|
0.333333333
|
0.666666
|
30
|
0.5
|
0.008333
|
75
|
10
|
22
|
0.3125
|
0.6875
|
32
|
0.426666
|
0.005688
|
90
|
12
|
26
|
0.315789474
|
0.684210
|
38
|
0.422222
|
0.004691
|
105
|
14
|
36
|
0.28
|
0.72
|
50
|
0.476190
|
0.004535
|
120
|
15
|
41
|
0.267857143
|
0.732142
|
56
|
0.466666
|
0.003888
|
135
|
15
|
45
|
0.25
|
0.75
|
60
|
0.444444
|
0.003292
|
150
|
16
|
49
|
0.246153846
|
0.753846
|
65
|
0.433333
|
0.002888
|
165
|
18
|
67
|
0.211764706
|
0.788235
|
85
|
0.515151
|
0.003122
|
180
|
18
|
75
|
0.193548387
|
0.806451
|
93
|
0.516666
|
0.002870
|
195
|
19
|
81
|
0.19
|
0.81
|
100
|
0.512820
|
0.002629
|
210
|
19
|
82
|
0.188118812
|
0.811881
|
101
|
0.480952
|
0.002290
|
225
|
19
|
83
|
0.18627451
|
0.813725
|
102
|
0.453333
|
0.002014
|
240
|
20
|
85
|
0.19047619
|
0.809523
|
105
|
0.4375
|
0.001822
|
255
|
24
|
100
|
0.193548387
|
0.806451
|
124
|
0.486274
|
0.001906
|
270
|
25
|
105
|
0.192307692
|
0.807692
|
130
|
0.481481
|
0.001783
|
285
|
26
|
120
|
0.178082192
|
0.821917
|
146
|
0.512280
|
0.001797
|
300
|
26
|
138
|
0.158536585
|
0.841463
|
164
|
0.546666
|
0.001822
|
315
|
27
|
142
|
0.159763314
|
0.840236
|
169
|
0.536507
|
0.001703
|
330
|
28
|
151
|
0.156424581
|
0.843575
|
179
|
0.542424
|
0.001643
|
345
|
30
|
163
|
0.155440415
|
0.844559
|
193
|
0.559420
|
0.001621
|
360
|
31
|
168
|
0.155778894
|
0.844221
|
199
|
0.552777
|
0.001535
|
375
|
32
|
171
|
0.157635468
|
0.842364
|
203
|
0.541333
|
0.001443
|
390
|
34
|
179
|
0.159624413
|
0.840375
|
213
|
0.546153
|
0.001400
|
405
|
35
|
187
|
0.157657658
|
0.842342
|
222
|
0.548148
|
0.001353
|
420
|
36
|
191
|
0.158590308
|
0.841409
|
227
|
0.540476
|
0.001286
|
435
|
37
|
202
|
0.154811715
|
0.845188
|
239
|
0.549425
|
0.001263
|
450
|
38
|
205
|
0.156378601
|
0.843621
|
243
|
0.54
|
0.0012
|
465
|
38
|
205
|
0.156378601
|
0.843621
|
243
|
0.522580
|
0.001123
|
480
|
38
|
206
|
0.155737705
|
0.844262
|
244
|
0.508333
|
0.001059
|
495
|
38
|
207
|
0.155102041
|
0.844897
|
245
|
0.494949
|
0.000999
|
510
|
40
|
209
|
0.16064257
|
0.839357
|
249
|
0.488235
|
0.000957
|
525
|
41
|
210
|
0.163346614
|
0.836653
|
251
|
0.478095
|
0.000910
|
540
|
41
|
212
|
0.162055336
|
0.837944
|
253
|
0.468518
|
0.000867
|
Table 2. The value of some parameters for the unstructured
interview method (M2).
Examining the tables, we see that the problem P possesses a finite, cumulative
function (Kf*(t)) whose time of elicitation
(te) is 450 minutes and 540 minutes respectively for the structured
interview and the unstructured interview
At this point, we can obtain all parameters defined in Section 4. Some of these
are indicated in Table 3, where M1 and M2 respectively
stand for the structured interview and the unstructured interview.
|
te
|
Kf*(
te)
|
pc
|
pnc
|
SEm
|
AEm
|
REET
|
|
|
|
|
|
|
|
M1
|
450
|
280
|
0.247
|
0.751
|
0.686
|
0.0079
|
0.93
|
M2
|
540
|
253
|
0.203
|
0.796
|
0.517
|
0.0046
|
1
|
Table 3. Calculation of some parameters for comparing M1 and
M2.
By looking at the information in the above tables, and by taking into account
the contents of the previous section, we can obtain several useful results for
P and the family (class) of problems to which P belongs. Some of these results
are the following:
1. The KEP with M2 takes 20% longer than with M1. So,
M2 is lazier than M1.
2. M1 introduces more complexity in the KEP than M2 does,
because the amount of knowledge obtained after applying M1 is over
9% more than the amount after applying M2.
3. The average density of concept knowledge is higher for M1, the
average density of non-concept knowledge being, hence, lower for
M1.
4. The average speedup of knowledge elicitation, as well as the average
acceleration of knowledge elicitation is higher for M1.
5. The sleeping time for M2 is zero, which implies that its relative
time of effective elicitation (REET) is 100%. With M1, 93% of the
time dedicated to the KEP is used to elicit relevant knowledge.
In other words, M1 is less lazy, more concept-complex and more
dynamic (i.e., its speedup and its acceleration are higher) than M2,
although M1 introduces a little more complexity than M2
does, and the REET corresponding to M1 is near to that of
M2. So, it seems that the structured interview method is better than
the unstructured one for this kind of problem, under the assumptions pointed
out previously.
6 Conclusions
In real world applications, the knowledge elicitation process is a time
consuming and hence influential cost-determining factor for developing
knowledge-based systems. Comparing elicitation techniques formally is an
interesting endeavour because it enables us to select the best elicitation
technique in a particular situation. This might lead to lower development
costs.
The knowledge elicitation process is influenced by various factors, including
the number of experts, the kind of problem, the context in which the
elicitation process takes place, and even the person who elicits the knowledge
by interacting with the experts. In order to formally compare these techniques,
we propose a simple semantics based on the following assumptions: (1) there are
different tasks involved in the problem for which a KBS has to be developed,
(2) there are various experts participating in that project (at least one for
each task), (3) every current knowledge elicitation technique is available, (4)
the person who elicits the knowledge is the same during the entire project, and
(5) the knowledge elicitation sessions do not invalidate knowledge elicited in
previous sessions.
For problems that satisfy these assumptions, and where the knowledge is limited
to concepts and some well-defined relationships between them, we defined, in a
step-by-step process, a set of mathematical functions which operate on
cumulative knowledge. Moreover, by sampling the values corresponding to these
functions during the knowledge elicitation process, a number of formal
parameters are suggested which can be used for comparing different knowledge
elicitation techniques.
To illustrate the usefulness of the mathematical artefacts designed in this
study, we showed an example where the mentioned parameters are applied to
compare the structured interview with the unstructured one. Both techniques
have been applied to a real problem involving environmental planning by
assessment in Spain. The results demonstrate that the structured interview
method is more appropriate than the unstructured one under the assumptions
pointed out above and for the assessment problem that we were concerned with.
Although, in this study, we have compared only two elicitation techniques, and
the final result is not a surprise (i.e., the structured interview is more
efficient than the unstructured one), we believe that the formal parameters can
be used to compare any two elicitation techniques, provided that the problem at
hand satisfies the identified assumptions (i.e., is KE-solvable).
Acknowledgements
This work has been supported by an institutional research grant from the
Spanish Council for Scientific Research (CSIC) and by the Netherlands Computer
Science Research Foundation with financial support from the Netherlands
Organisation for Scientific Research (NWO).
References
>Bell, J., and Hardiman, R. J. (1989). The third role - the naturalistic
knowledge engineer, in D. Diaper (Eds.), Knowledge engineering: Principles,
techniques, and applications. Chichester: Ellis Horwood Ltd.
Berry, D. C. (1987). The problem of implicit knowledge, Expert Systems,
Vol. 4:144-151.
Burton, A. M., Shadbolt, N. R., Rugg, G., and Hedgecock, A. P. (1990). The
Efficacy of Knowledge Elicitation Techniques: a Comparison Across Domains and
Levels of Expertise, Knowledge Acquisition, Vol. 2: 167-178.
Kang, H. B., Compton, P., and Preston, P. (1995). Multiple classification
ripple down rules: evaluation and possibilities, in B. R. Gaines, and M. Musen
(Eds.), Proceedings of the Ninth Banff Knowledge Acquisition for
Knowledge-Based Systems Workshop, Vol. 1:17.1-17.20.
Cooke, N. J. (1994).Varieties of knowledge elicitation techniques,
International Journal of Human-Computer Studies, Vol.
41:801-849.
Gammack, J. (1992). Knowledge engineering issues for decision support, in G.
Wright, and F. Bolger (Eds.), Expertise and Decision Support, 203-226,
Plenum Press.
Gisolfi, A., and Di Lascio, L. (1995). POTCLAS: a fuzzy expert system for the
classification of archaeological pottery fragments, International Journal of
Expert Systems, Vol. 8, No. 2 :145-164.
Goldszmidt, M., and Pearl, J. (1991). On the consistency of defeasible
databases, Artificial Intelligence, Vol. 52:121-149.
Hart, A. (1986). Knowledge Acquisition for expert systems, Tiptree,
Essex: Anchor Brendon Ltd.
Hunt, R., Middleton, D. A. J., Grime, J. P., and Hodgson, J. G. (1991).
TRISTAR: an expert system for vegetation processes, Expert Systems, Vol.
8: 219-226.
Hwang, G-J. (1995). Knowledge acquisition for fuzzy expert systems,
International Journal of Intelligent Systems, Vol. 10:541-560.
Lehmann, D., and Magidor, M. (1992). What does a conditional knowledge base
entail?, Artificial Intelligence, Vol. 55:1-60.
Marcus, S. (1988). Automating knowledge acquisition for expert systems,
Boston: Kluwer Publisher.
Martinez-Bejar, R., Castillo, V. M., and Martin, F. (1995). A knowledge-based
approach for landscape study in natural resources physical planning (in
Spanish), in R. Rizo, and J. M. Garcia (Eds.), Technological Transference of
Artificial Intelligence to Industry, Medicine and Social Applications,
209-216, Universidad de Alicante.
MOPT. (1992). A Guidebook for making physical environment studies (in
Spanish), MOPU, Madrid: Secretaría de Estado para las
Políticas del Agua y el Medio Ambiente.
Nisbett, R. E., and Wilson, T. D. (1977). Telling more than we can know: verbal
reports on mental processes, Psychological Review, Vol.
84:231-259.
O'Hara, K., Motta, E., and Shadbolt, N. (1994). Grounding GDMs: A Structured
Case Study, International Journal of Human-Computer Studies, Vol.
40: 315-347.
Puerta, A. R., Egar, J., Tu, S., and Musen, M. (1992). A Multiple-Method Shell
for the Automatic Generation of Knowledge Acquisition Tools, Knowledge
Acquisition, Vol. 4:171-196.
Runkel, J. T., and Birmingham, W. P. (1993). Knowledge acquisition in the
small: building knowledge-acquisition tools from pieces, Knowledge
Acquisition, Vol. 5:221-243.
Starfield, A. M., and Bleloch, A. L. (1983). Expert Systems: An approach to
problems in ecological management that are difficult to quantify, Journal of
Environmental Management, Vol. 16: 261-268.
Welbank, M. (1983). A review of knowledge acquisition techniques for expert
systems, British Telecommunications Research Laboratories Technical Report,
Ipswich, England: Martlesham Heath.
Wielinga, B. J., Schreiber, A. T., and Breuker, J. A. (1992). KADS: a modelling
approach to knowledge engineering, Knowledge Acquisition, Vol.
4:5-53.
[1] The term visual fragility of a
landscape refers to its sensitivity to changes caused by human activities
(MOPT, 1992).
[2] Decision rules are the rules the expert uses
to solve the problem. Note that, although we use (production) rules in the
formalisation, the rule format as such is not essential. What is essential, is
some kind of carrier of concepts and relations. In this paper, we use rules
because the experts involved in the case-study expressed themselves through
rules.
[3] The term "concepts" comprises the
relevant objects needed to represent and solve the problem.
[4] For an overview of the different ways in
which experts can participate in the KEP, see Cooke (1994).
[5] We assume that experts participating in a
KEP effectively can detect non-relevant knowledge whenever needed.
[6] In this article, landscape study and
landscape study task are used as synonyms.
 ASS(r), and that the property u
ASS(r), and that the property u
 PRO(r,z), VAL(r,z,u) provides the value corresponding to the
concept z for the property u in such a way that it can explicitly be extracted
from r. Possible ambiguity problems can be solved by introducing the notation
concept.property.value, where value is equal to VAL(r,z,u);
property is the property referenced by value, that is, u;
concept is the concept to which value is linked, that is,
z.
PRO(r,z), VAL(r,z,u) provides the value corresponding to the
concept z for the property u in such a way that it can explicitly be extracted
from r. Possible ambiguity problems can be solved by introducing the notation
concept.property.value, where value is equal to VAL(r,z,u);
property is the property referenced by value, that is, u;
concept is the concept to which value is linked, that is,
z. EPRO(Kru(t), Kc(t))
EPRO(Kru(t), Kc(t)) 

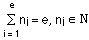 .
.