

Next: Resolution methods
Up: KL-components
Previous: Ontologies
A model abstracts certain aspects from reality. It identifies objects,
relationships, properties and attributes of the objects, relationships
between objects and properties of objects, and so on. It is formally
described by an order-sorted theory that imports the ontologies it
uses to represent its knowledge. The knowledge representation
formalism and contents of a model are respectively described by the
axiom schemas (which make the syntactical structure of its
axioms explicit) and axioms parts of its formal description.

import  *
*
sorts sort tree
constants (constantsymbol +: sortsymbol) *
functions (functionsymbol +: sortsymb  sortsymbol) *
sortsymbol) *
predicates (predicatesymbol +: sortsymbol *)
*
variables (variablesymbol +: sortsymbol) *
axiom schemas (formulaschema +: metavariable)
*
axioms (formula) *
The following examples show the formal descriptions of some models
which use the ontology defined in the previous example.
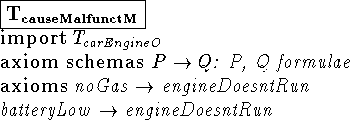 \
\
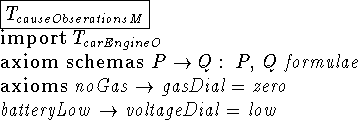
 \
\

jsierra@cs.stanford.edu
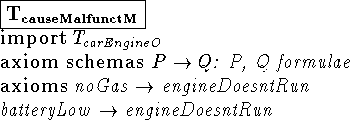 \
\
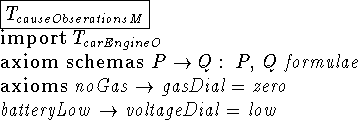
 \
\
