Ontologies and the Configuration of Problem-Solving Methods
Rudi Studer1, Henrik Eriksson2, John Gennari3,
Samson Tu3, Dieter Fensel1,4, and Mark Musen3
1 Institute AIFB, University of Karlsruhe, D-76128 Karlsruhe
e-mail: studer@aifb.uni-karlsruhe.de
2 Department of Computer and Information Science, Linköping University, S-58183 Linköping
e-mail: her@ida.liu.se
3 Section on Medical Informatics, Knowledge Systems Laboratory, Stanford University School of Medicine, Stanford, CA 94305-5479, USA
e-mail: {gennari,tu,musen}@camis.stanford.edu
4 Department SWI, University of Amsterdam, NL-1018 WB Amsterdam
e-mail: dieter@swi.psy.uva.nl
Abstract
Problem-solving methods model the problem-solving behavior of knowledge-based systems. The PROTÉGÉ-II framework includes a library of problem-solving methods that can be viewed as reusable components. For developers to use these components as building blocks in the construction of methods for new tasks, they must configure the components to fit with each other and with the needs of the new task. As part of this configuration process, developers must relate the ontologies of the generic methods to the ontologies associated with other methods and submethods. We present a model of method configuration that incorporates the use of several ontologies in multiple levels of methods and submethods, and we illustrate the approach by providing examples of the configuration of the board-game method.
1. Introduction
Problem-solving methods for knowledge-based systems capture the problem-solving behavior required to performing the system's task (McDermott, 1988). Because certain tasks are common (e.g., planning and configuration), and are approachable by the same problem-solving behavior, developers can reuse problem-solving methods in several applications ((Chandrasekaran and Johnson, 1993), (Breuker and Van de Velde, 1994)). Thus, a library of reusable methods would allow the developer to create new systems by selecting, adapting and configuring such methods. Moreover, development tools, such as PROTÉGÉ-II (Puerta et al., 1992), can support the developer in the reuse of methods.
Problem-solving methods are abstract descriptions of problem-solving behavior. The development of problem solvers from reusable components is analogous to the general approach of software reuse. In knowledge engineering as well as software engineering, developers often duplicate work on similar software components, which are used in different applications. The reuse of software components across several applications is a potentially useful technique that promises to improve the software-development process (Krueger, 1992). Similarly, the reuse of problem-solving methods can improve the quality, reliability, and maintainability of the software (e.g., by the reuse of quality-proven components). Of course, software reuse is only financially beneficial in the end if the indexing and configuration overhead is less than the effort that is needed to create the required component several times from scratch.
Although software reuse is an appealing approach theoretically, there are serious practical problems associated with reuse. Two of the most important impediments to software reuse are (1) the problem of finding reusable components (e.g., locating appropriate components in a library), and (2) the problem of adapting reusable components to their task and to their environment. The first problem is sometimes called the indexing problem, and the second problem is sometimes called the configuration problem. These problems are also present in the context of reusable problem-solving methods. In the remainder of this paper we shall focus on the configuration problem.
Method configuration is a difficult task, because the output of one method may not correspond to the input of the next method, and because the method may have subtasks, which are solved by submethods offering a functionality that is different from the assumptions of the subtask. Domain-independent methods use a method ontology, which, for example, might include concepts such as states, transitions, locations, moves, and constraints, whereas the user input and the (domain-specific) knowledge-base use a domain-oriented ontology, which might include concepts such as office workers, office rooms, and room-assignment constraints. Thus, a related issue to the configuration problem is the problem of mappings between ontologies (Gennari et al., 1994).
In this paper, we shall address the configuration problem. The problems of how to organize a library of problem-solving methods and of how to select an appropriate method from such a library are beyond the scope of the paper. We shall introduce an approach for handling method ontologies when configuring a method from more elementary submethods. In our framework, configuration of a method means selecting appropriate submethods for solving the subtasks of which a method is composed. We introduce the notion of a subtask ontology in order to be able (i) to make the ontology of a method independent of the submethods that are chosen to solve its subtasks, and (ii) to specify how a selected submethod is adapted to its subtask environment. Our approach supports such a configuration process on multiple levels of subtasks and submethods. Furthermore, the access of domain knowledge is organized in such a way that no mapping of domain knowledge between the different subtask/submethod levels is required.
The approach which is described in this paper provides a framework for handling some important aspects of the method configuration problem. However, our framework does not provide a complete solution to this problem. Furthermore, the proposed framework needs in the future a thorough practical evaluation by solving various application tasks.
The rest of this paper is organized as follows. Section 2 provides a background to PROTÉGÉ-II, the board-game method, and the MIKE approach. Section 3 introduces the notions of method and subtask ontologies and discusses their relationships with the interface specification of methods and subtasks, respectively. Section 4 analyses the role of ontologies for the configuration of problem-solving methods and presents a model for configuring a problem-solving method from more elementary submethods that perform the subtasks of the given problem-solving method. In Sections 5 and 6, we discuss the results, and draw conclusions, respectively.
2. Background: PROTÉGÉ-II, the Board-Game Method, and MIKE
In this section, we shall give a brief introduction into PROTÉGÉ-II and MIKE (Angele et al., 1996b) and will describe the board-game method (Eriksson et al., 1995) since this method will be used to illustrate our approach.
2.1 Method Reuse for PROTÉGÉ-II
PROTÉGÉ-II (Puerta et al., 1992, Gennari et al., 1994, Eriksson et al., 1995) is a methodology and suite of tools for constructing knowledge-based systems. The PROTÉGÉ-II methodology emphasizes the reuse of components, including problem-solving methods, ontologies, and knowledge-bases.
PROTÉGÉ-II allows developers to reuse library methods and to generate custom-tailored knowledge-acquisition tools from ontologies. Domain experts can then use these knowledge-acquisition tools to create knowledge bases for the problem solvers. In addition to developing tool support for knowledge-based systems, PROTÉGÉ-II is also a research project aimed at understanding the reuse of problem-solving methods, and at alternative approaches to reuse. Naturally, the configuration of problem-solving methods for new tasks is a critical step in the reuse process, and an important research issue for environments such as PROTÉGÉ-II.
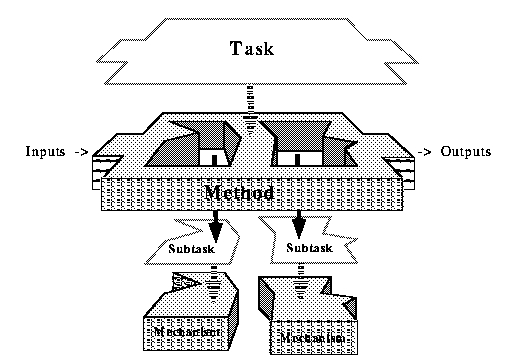
The model of reuse for PROTÉGÉ-II includes the notion of a library of reusable problem-solving methods (PSMs) that perform tasks. PROTÉGÉ-II uses the term task to indicate the computations and inferences a method should perform in terms of its input and output. (Note that the term task is used sometimes in other contexts to indicate the overall role of an application system, or the application task.) In PROTÉGÉ-II problem-solving methods are decomposable into subtasks. Other methods, sometimes called submethods, can perform these subtasks. Primitive methods that cannot be decomposed further are called mechanisms. This decomposition of tasks into methods and mechanisms is shown graphically in Figure 2-1.
Submethods and mechanisms should be reusable by developers as they build a solution to a particular problem. Thus, the developer should be able to select a generic method that performs a task, and then configure this method by selecting and substituting appropriate submethods and mechanisms to perform the method's subtasks. Note that because the input-output requirements of tasks and subtasks often differ from the input-output assumptions of preexisting methods and mechanisms, we must introduce mappings among the task (or subtask) and method (or submethod) ontologies.

Figure 2-1: Method-subtask decomposition in PROTÉGÉ-II
PROTÉGÉ-II uses three major types of ontologies for defining various aspects of the knowledge-based system: domain, method, and application ontologies. Domain ontologies model concepts and relationships for a particular domain of interest. Ideally, these ontologies should be partititioned so as to separate those parts that may be more dependent on the problem-solving method. Method ontologies model concepts related to problem-solving methods, including input and output assumptions. To enable reuse, method ontologies should be domain-independent. In most situations, reusable domain and method ontologies by themselves are insufficient for a complete application system. Thus, PROTÉGÉ-II uses an application ontology that combines domain and method ontologies for a particular application. Application ontologies are used to generate domain-specific, method-specific knowledge-acquisition tools.
The focus of this paper is on the configuration of problem-solving methods and submethods. Thus, we will describe method ontologies (see Section 3), rather than domain or application ontologies, and the mappings among tasks and methods that are necessary for method configuration (see Section 4).
2.2 The Board-Game Method (BGM)
We shall use the board-game method ((Eriksson et al., 1995), (Fensel et al., 1996a)) as a sample method to illustrate method configuration in the PROTÉGÉ-II framework. The basic idea behind the board-game method is that the method should provide a conceptual model of a board game where game pieces move between locations on a board (see Figure 2-2). The state of such a board game is defined by a set of assignments specifying which pieces are assigned to which locations. Developers can use this method to perform tasks that they can model as board-game problems.
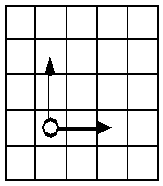
Figure 2-2: The board-game method provides a conceptual model where pieces move between locations.
To configure the board-game method for a new game, the developer must define among other the pieces, locations, moves, the initial state and goal states of the game. The method operates by searching the space of legal moves, and by determining and applying the most promising moves until the game reaches a goal state. The major advantage of the board-game method is that the notion of a board game as the basis for the method configuration, makes the method convenient to reuse for the developer.
We have used the board-game method in different configurations to perform several tasks. Examples of such tasks are the towers-of-Hanoi, the cannibals-and-missionaries, and the Sisyphus room-assignment (Linster, 1994) problem. By modeling other types of tasks as board games, the board-game method can perform tasks beyond simple games. The board-game method can perform the Sisyphus room-assignment task, for instance, if we (1) model the office workers as pieces, (2) start from a state where all the workers are at a location outside the building, and (3) move the workers one by one to appropriate rooms under the room-assignment constraints.
2.3 The MIKE Approach
The MIKE approach (Model-based and Incremental Knowledge Engineering) (Angele et al., 1996b) aims at providing a development method for knowledge-based systems covering all steps from knowledge acquisition to design and implementation. As part of the MIKE approach the Knowledge Acquisition and Representation Language KARL (Fensel et al., 1996c), (Fensel, 1995) has been developed. KARL is a formal and operational knowledge modeling language which can be used to formally specify a KADS like model of expertise (Schreiber et al., 1993). Such a model of expertise is split up into three layers:
The domain layer contains the domain model with knowledge about concepts, their features, and their relationships. The inference layer contains a specifiation of the single inference steps as well as a specification of the knowledge roles which indicate in which way domain knowledge is used within the problem solving steps. In MIKE three types of knowledge roles are distinguished: Stores are used as containers which provide input data to inference actions or collect output data generated by inference actions. Views and terminators are used to connect the (generic) inference layer with the domain layer: Views provide means for delivering domain knowledge to inference actions and to transform the domain specific terminology into the generic PSM specific terminology. In an analogous way, terminators may be used to write the results of the problem solving process back to the domain layer and thus to reformulate the results in domain specific terms. The task layer contains a specification of the control flow for the inference steps as defined on the inference layer.
For the remainder of the paper, it is important to know that in KARL a problem solving method is specified in a generic way on the inference and task layer of a model of expertise. A main characteristic of KARL is the integration of object orientation into a logical framework. KARL provides classes and predicates for specifying concepts and relationships, respectively. Furthermore, classes are characterized by single- and multi-valued attributes and are embedded in an is-a hierarchy. For all these modeling primitives, KARL offers corresponding graphical representations. Finally, sufficient and necessary constraints, which have to be met by class and predicate definitions, may be specified using first-order formulae.
Currently, a new version of KARL is under development which among others will provide the notion of a method ontology and will provide primitives for specifying pre- and postconditions for a PSM (Angele et al., 1996a). Thus, this new version of KARL includes all the modeling primitives which are needed to formally describe the knowledge-level framework which shall be introduced in Sections 3 and 4. However, this formal specification is beyond the scope of this paper.
3. Problem-Solving Method Ontologies
When describing a PSM, various characteristic features may be identified, such as the input/output behavior or the knowledge assumptions on which the PSM is based (Fensel, 1995a), (Fensel et al., 1996b). In the context of this paper, we will consider a further characteristic aspect of a PSM: its ontological assumptions. These assumptions specify what kind of generic concepts and relationships are inherent for the given PSM. In the framework of PROTÉGÉ-II, these assumptions are captured in the method ontology (Gennari et al.,1994).
Subsequently, we define the notions of a method ontology and of a subtask ontology, and discuss the relationship between the method ontology and the subtask ontologies associated with the subtasks of which the PSM is composed. For that discussion we assume that a PSM comes with an interface specification that describes which generic external knowledge roles (Fensel, 1995b) are used as input and output. Each role includes the definition of concepts and relationships for specifying the terminology used within the role.
Fig. 3-1 shows the interface specification of the board-game method. We see, for instance, that knowledge about moves, preferences among moves, and applicability conditions for moves is provided by the input roles "Moves", "Preferred_Moves", and "Applic_Moves" (applicable moves), respectively; within the role "Moves" the concept "moves" is defined, whereas for example within the role "Preferred_Moves" the relationship "prefer_m" is defined which specifies a preference relation between two moves for a given state (see Fig. 3-3).
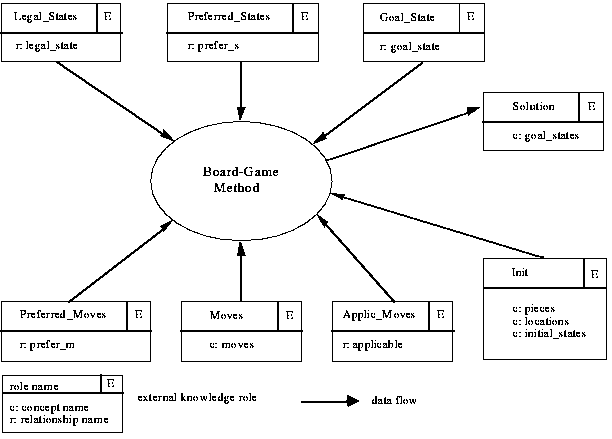
Figure 3-1: The interface of the board-game method
Since the context in which the method will be used is not known in advance, one cannot specify which input knowledge is delivered from other tasks as output and which input knowledge has to be taken from the domain. Therefore, besides the output role "Solution", all other input roles are handled homogenously (that is, as external input knowledge roles).
The interface description determines in which way a method can be adapted to its calling environment: a subset of the external input roles will be used later on as domain views (that is for defining the mapping between the domain-specific knowledge and the generic PSM knowledge).
3.1 Method Ontologies
We first consider the situation that a complete PSM is given as a building block in the library of PSMs. In this case, a PSM comes with a top-level ontology, its method ontology, specifying all the generic concepts and relationships that are used by the PSM for providing its functionality. This method ontology is divided into two parts:
(i) Global definitions, which include all generic concept and relationship definitions that are part of the interface specification of the PSM (that is, the external input and output knowledge roles of the PSM, respectively). For each concept or relationship definition, it is possible to indicate whether it is used as input or as output (however, that does not hold for subordinate concept definitions, i.e. concepts that are just used as range restrictions of concept attributes, or for high-level concepts that are just used for introducing attributes which are inherited by subconcepts). Thus, the ontology specifies clearly which type of generic knowledge is expected as input, and which type of generic knowledge is provided as output.
(ii) Internal definitions, which specify all concepts and relationships that are used for defining the dataflow within the PSM (that is, they are defined within stores).
Within both parts, constraints can be specified for further restricting the defined terminology. It should be clear that the global definitions are exactly those definitions that specify the ontological assumptions that must be met for applying the PSM.
We assume that a PSM that is stored in the library comes with an ontology description at two levels of refinement. First, a compact representation is given that just lists the names of the concepts and relationships of which the ontology is composed. This compact representation also includes the distinctions of global and internal definitions. It is used for providing an initial, not too detailed overview about the method ontology.
Fig. 3-2 shows this compact representation of the board-game method ontology. We see that for instance "moves" is an input concept, "prefer_m" (preference of moves) is an input relationship, and "goal-states" is an output concept; "assignments" is an example of a subordinate concept which is used within state definitions, whereas "movable_objects" is an example of a high level concept. Properties of "movable_objects" are for instance inherited by the concept "pieces" (see below). As we will see later on, the concept "current-states" is part of the internal definitions, since it is used within the board game method for specifying the data flow between subtasks (see Section 3.2)
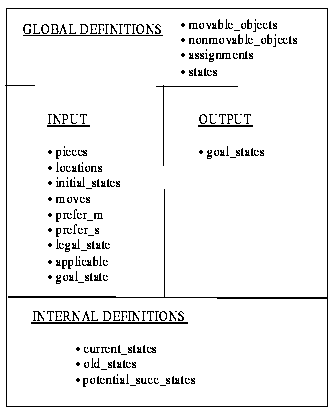
Figure 3-2: The compact representation of the ontology of the board-game method
Second, a complete specification of the method ontology is given. We use KARL for formally specifying such an ontology which provides all concept and relationship definitions as well as all constraints. Fig. 3-3 gives a graphic KARL representation of the board-game method ontology (not including constraints). We can see that for instance a move defines a new location for a given piece (single-valued attribute "new_assign" with domain "moves" and range "assignments") or that the preference between moves is state dependent (relationship "prefer_m"). The attribute "assign" is an example of a multi-valued attribute since states consist of a set of assignments.

Figure: 3-3: The graphic KARL representation of the board-game method ontology
When comparing the interface specification (Fig. 3-1) and the method ontology (Fig. 3-3) we can see that the union of the terminology of the external knowledge roles is equal to the set of global definitions being found in the method ontology.
3.2 Subtask Ontologies
In general, within the PROTÉGÉ-II framework, a PSM is decomposed into several subtasks. Each subtask may be decomposed in turn again by choosing more elementary methods for solving it. We generalize this approach in the sense that, for trivial subtasks, we do not distinguish between the subtasks and the also trivial mechanisms for solving them. Instead, we use the notion of an elementary inference action (Fensel et al., 1996c). In the given context, such an elementary inference action may be interpreted as a "hardwired" mechanism for solving a subtask. Thus, for trivial subtasks, we can avoid the overhead that is needed for associating a subtask with its corresponding method (see below). That is, in general we assume that a method can be decomposed into subtasks and elementary inference actions.
When specifying a PSM, a crucial design decision is the decomposition of the PSM into its top-level subtasks. Since subtasks provide the slots where more elementary methods can be plugged in, the type and number of subtasks determine in which way a PSM can be configured from other methods. As a consequence, the adaptability of a PSM is characterized by the knowledge roles of its interface description, and by its top-level task decomposition.
For a complete description of the decomposition structure of a PSM, one also has to specify the interfaces of the subtasks and inference actions, as well as the data and control flow among these constituents. The interface of a subtask consists of knowledge roles, which are either external knowledge roles or (internal) stores, which handle the input/output from/to other subtasks and inference actions. Some of these aspects are described for the BGM in Figures 3-4 and 3-5, respectively.
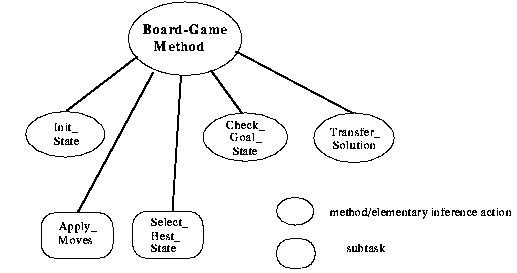
Figure 3-4: The top-level decomposition of the board-game method
into elementary inference actions and subtasks
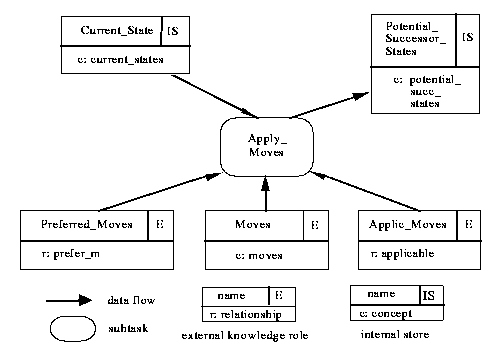
Figure 3-5: The interface of the subtask "Apply_Moves"
Fig. 3-4 shows the decomposition of the board-game method into top-level subtasks and elementary inference actions. We can see two subtasks ("Apply_Moves" and "Select_Best_State") and three elementary inference actions ("Init_State", "Check_Goal_State", "Transfer_Solution"). This decomposition structure specifies clearly that the board-game method may be configured by selecting appropriate methods for solving the subtasks "Apply_Moves" and "Select_Best_State".
In Fig. 3-5 the interface of the subtask "Apply_Moves" is shown. The interface specifies that "Apply_Moves" receives (board-game method) internal input from the store "Current_State" and delivers output to the store "Potential_Successor_States". Furthermore, three external knowledge roles provide the task- and/or domain-specific knowledge that is required for performing the subtask "Apply_Moves".
Having introduced the notion of a method ontology, the problem arises how that method ontology can be made independent of the selection of (more elementary) methods for solving the subtasks of the PSM. The basic idea for getting rid of this problem is that each subtask is associated with a subtask ontology. The method ontology is then essentially derived from these subtask ontologies by combining the different subtask ontologies, and by introducing additional superconcepts, like for example the concept "movable_objects" (compare Fig. 3-2). Of course, the terminology associated with the elementary inference actions has to be considered in addition.
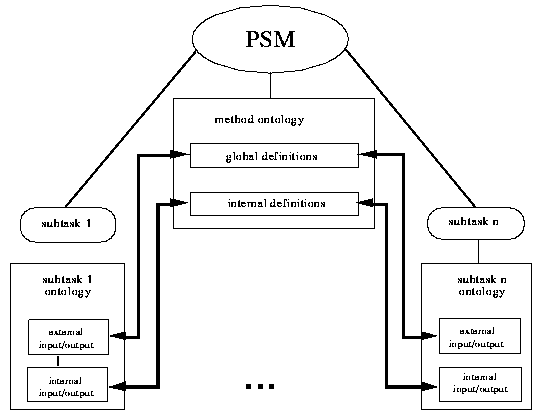
Figure: 3-6: The method ontology and the related subtask ontologies
The notion of subtask ontologies has two advantages:
1) By building up the method ontology from the various subtask ontologies, the method ontology is independent of the decision which submethod will be used for solving which subtask. Thus, a configuration independent ontology definition can be given for each PSM in the library.
2) Subtask ontologies provide a context for mapping the ontologies of the submethods, which are selected to solve the subtasks, to the global method ontology (see Section 4).
The type of mapping that is required between the subtask ontology and the ontology of the method used to solve the subtask is dependent on the distinction of input and output definitions within the subtask ontology (see Section 4). Therefore, we again separate the subtask ontology appropriately. In addition, a distinction is made between internal and external input/output. The feature "internal" is used for indicating that this part of the ontology is used within the method of which the subtask is a part (that is, for defining the terminology of the stores used for the data flow among the subtasks which corresponds to the internal-definitions part of the method ontology). The feature "external" indicates that input is received from the calling environment of the method of which the subtask is a part, or that output is delivered to that calling environment (that corresponds to the global-definitions part of the method ontology). This distinction can be made on the basis of the data dependencies defined among the various subtasks (see Fig. 3-6).
In Fig. 3-7, we introduce the ontology for the subtask "Apply_Moves". According to the interface description which is given in Fig. 3-5, we assume that the current state is an internal input for "Apply_Moves", whereas the potential successor states are treated as internal output. Moves, preferences among moves, and applicability conditions for moves are handled as external input.
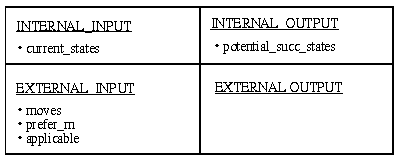
Figure 3-7: The compact representation of the "Apply_Moves" subtask ontology
When investigating the interface and ontology specification of a subtask, one can easily recognize that even after having introduced the subtask decomposition, it is still open as to what kind of external knowledge is taken from the domain and what kind of knowledge is received as output from another task. That is, in a complex application task environment, in which the board-game method is used to solve, for example, a subtask st1, it depends on the calling environment of st1 whether, e.g., the preference of moves ("prefer_m") has to be defined in a mapping from the domain, or is just delivered as output from another subtask st2, which is called before st1 is called.
4. Configuring Problem Solving Methods from More Elementary Methods
The basic idea when building up a library of PSMs is that one does not simply store completely defined PSMs. In order to achieve more flexibility in adapting a PSM from the library to its task environment, concepts are required for configuring a PSM from more elementary building blocks (i.e., from more elementary methods (Puerta et al., 1992)). Besides being more flexible, such a configuration approach also provides means for reusing these building blocks in different contexts.
Based on the structure introduced in Section 3, the configuration of a PSM from building blocks requires the selection of methods that are appropriate for solving the subtasks of the PSM. Since we do not consider the indexing and adaptation problem in this paper, we assume subsequently, that we have found a suitable (sub-)method for solving a given subtask, e.g. by exploiting appropriate semantic descriptions of the stored methods. Such semantic descriptions could, for instance, be pre-/postconditions which specify the functional behavior of a method (Fensel et al., 1996b). By using the new version of KARL (Angele et al., 1996a) such pre-/postconditions can be specified in a completely formal way.
We shall illustrate our approach by discussing how we can use the method "Determine_Assignments" (see Section 4.1.1) for solving the subtask "Apply_Moves".
For applying a method to solve a subtask, two problems have to be addressed:
1) We have to establish a correspondence between the interface description of the subtask and the interface description of the selected method.
2) We have to define mappings relating the subtask ontology to the method ontology.
4.1 Establishing a Correspondence between the Interface Descriptions
Let us first consider the problem of establishing a correspondence between the interface of the subtask and the interface of the method: One has to determine which external knowledge role of the method is associated with which knowledge role of the subtask. Of course, for establishing these correspondences one has to investigate the concept and relationship definitions of the respective knowledge roles as well. Furthermore, since for each subtask we distinguish whether a knowledge role is a store or an external knowledge role, the interface "matching" results in the decision which roles of the method are associated with stores and which are associated with external knowledge roles. This decision is crucial later on, since - as we will see in Section 4.2 - method roles, which are associated with external knowledge roles of the subtask, may be handled as domain views or terminators (compare Section 2.3) in the end.
When comparing the interface descriptions, several different situations may arise:
(i) There is a one-to-one correspondence between the knowledge roles of the subtask on the one hand and the external knowledge roles of the method on the other hand.
In this case, the "matching" is trivial.
(ii) There does not exist a one-to-one correspondence between the input knowledge roles in the substask description and the input knowledge roles in the method interface.
When there exists only a structural mismatch between the two interface descriptions (that is, the number of roles is different, however corresponding concept and relationship definitions may be identified), one has to define appropriate mappings for relating the subtask and method ontology (see Section 4.2).
When the input knowledge roles of the subtask do not provide all the concepts and relationships that are required by the selected method, there exist several alternatives to handle this situation: First, the missing knowledge is provided by mappings from the domain (that is, the corresponding external input knowledge roles of the method are handled as views (compare Section 2.3)). Second, the subtask description is extended by the input knowledge roles currently missing. Of course, this means that other subtasks must be modified in such a way that they provide the data for filling these additional roles. Third, the knowledge that is required to fill the additional external input knowledge roles has to be provided by the user as user input. It depends on the specific situation which of these alternatives is preferable.
(iii) There does not exist a one-to-one correspondence between the output knowledge roles in the subtask description and the output knowledge roles in the method interface.
The situation that the method is providing more output than is needed by the subtask environment, is a trivial case. However, if the method is not delivering all the output that is required one has to extend the method in an appropriate way to meet the requirements of the subtask.
It should be clear that in most real life situations one will have to adapt the interfaces to each other according to cases ii) and iii) in order to be able to use a selected method for solving a given subtask.
In order to able to illustrate that approach, we will subsequently introduce a method "Determine_Assignments", which will be used to solve the subtask "Apply_Moves" of the board-game method. This subtask is used for computing potential successor states by applying preferred moves that are applicable to the current state.
4.1.1 The Method "Determine_Assignments"
For solving the subtask "Apply_Moves", we assume the existence of a method "Determine_Assignments", which is stored in our method library. It is assumed that this method has been defined in the context of assignment tasks (see (Puppe, 1993)) and is able to determine new assignments given a state (a set of assignments). An assignment determines to which "supply" a "demand" has been assigned. That is, we assume two disjoint sets supplies and demands, and propose some assignments of demands to supplies (as a forward pointer: Supplies correspond to locations, demands to pieces in the board-game method context). Successor states are derived from the given state by adding new assignments to the given set of assignments.

Figure 4-1: The compact representation of the global definitions
of the ontology of "Determine_Assignments "
In Fig. 4-1, we give a partial definition of the ontology of "Determine_Assignments": An assignment defines a new supply for a given demand. Whereas the relationship "prefer_assignment" describes the state dependent preference between assignments, the relationship "allowed" is used for specifying which assignments are allowed in which state.
In the same way that we have defined the interface for the board-game method, we have to define the interface for the method "Determine_Assignments". In Fig. 4-2 we can see all the external knowledge roles which are used as input and output roles: given an input state, the method "Determine_Assignments" delivers a set of successor states by selecting some of the allowed assignments according to a preference relation and by then applying these preferred assignments.
Again, the collection of class and predicate definitions being found in the different external knowledge roles are identical to the global definitions given in the ontology specification.
4.1.2 Establishing the Correspondence between the Interfaces of the Method "Determine_Assignments" and the Subtask "Apply_Moves"
As we can see in Fig. 4-3 there is a structural mismatch between the external knowledge roles of the method "Determine_Assignments" and the knowledge roles of the subtask "Apply_Moves". The matching specifies for example, that
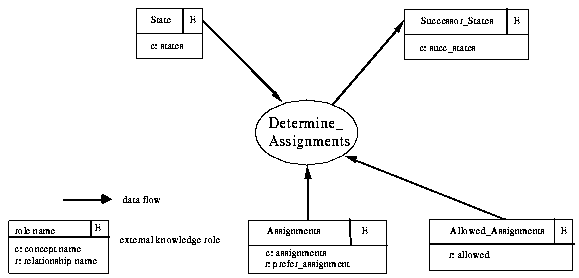
Figure 4-2: The interface of the method "Determine_Assignments"
(i) the external knowledge roles "State" and "Successor_States" are associated with the internal stores "Current_State" and "Potential_Successor_States", respectively, and that
(ii) the external knowledge role "Assignments" is associated with the external knowledge roles "Moves" and "Preferred_Moves", since "Assignments" provides both, the concept "assignments" and the relationship "prefer_assignment".
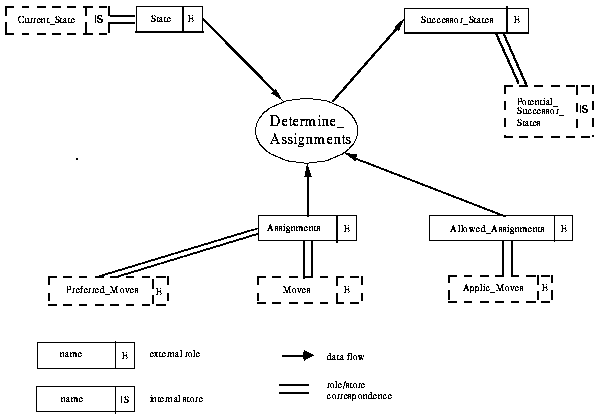
Figure 4-3: Matching of the interface of the method "Determine_Assignments" the with interface of the subtask "Apply_Moves"
Obviously, the matching of roles as black boxes is not sufficient. Rather, we have to consider how the subtask ontology and the ontology of the method that should be used to solve the subtask are related to each other. Of course, that mapping must be consistent with the method-subtask interface.
4.2 The Subtask to Method Mapping of Ontologies
The notion of subtask as introduced in Section 3 specifies, among other things, a subtask interface that defines which knowledge roles are used as external knowledge roles and which are used as stores. The concept and relationship definitions introduced within the stores and external knowledge roles are captured in the internal part of the subtask ontology and in the external part, respectively (compare Fig. 3-5 and Fig. 3-7). On the other hand, a sub-method comes with associated external knowledge roles. The concepts and relationships which are defined within these roles are reflected in the global definitions part of the sub-method ontology (compare Fig. 4-1 and Fig. 4-2).
To be able to supplement the interface matching between a subtask and its assigned submethod with the related ontology mapping, one has to specify how the external knowledge roles are handled. For that purpose, we first have to consider the method of which the subtask is a part. For each of the external input knowledge roles of this method the context in which the method is used determines
(i) whether the external knowledge is delivered from preceeding (sub-)tasks as output, or
(ii) whether the external knowledge has to be taken from the available domain knowledge[1].
In case (i), the external input knowledge roles are handled as (external) stores, whereas in case (ii) these roles are handled as views. In the same way, external output knowledge roles are interpreted as (external) stores and terminators, respectively. This distinction between (external) stores, views, and terminators is inherited by the top-level subtasks of the method. Thus, the calling environment of a method determines for each external knowledge role of its subtasks whether it is handled as an external (input or output) store, a view, or a terminator. In turn, this distinction is inherited by each of the (sub-)methods solving these subtasks.
Based on these distinctions, we are now able to define the ontology mapping:
(i) Input definitions of the subtask ontology that are used in internal or external input stores are downward mapped to input definitions of the (sub-)method ontology.
(ii) Output definitions of the (sub-)method ontology that are given in internal or external output stores are upward mapped to the output definitions of the subtask ontology.
(iii) For input definitions of the subtask ontology which are used in views, just a correspondence to the input definitions of the (sub-)method ontology is established. This means, that we do not really define a mapping; instead we specify which concept or relationship definition of the subtask ontology is associated with which definition in the (sub-) method ontology. Thus, the (sub-)method gets the information regarding which knowledge has to be taken from the domain knowledge. As a consequence, domain knowledge is always accessed within the method and never from a task. Furthermore, mappings of domain knowledge between subtasks and (sub-)methods are avoided, since domain knowledge is always accessed within a method on that level of refinement, where it is needed.
(iv) Output definitions of terminators are handled in an analogous way to the definitions of views.
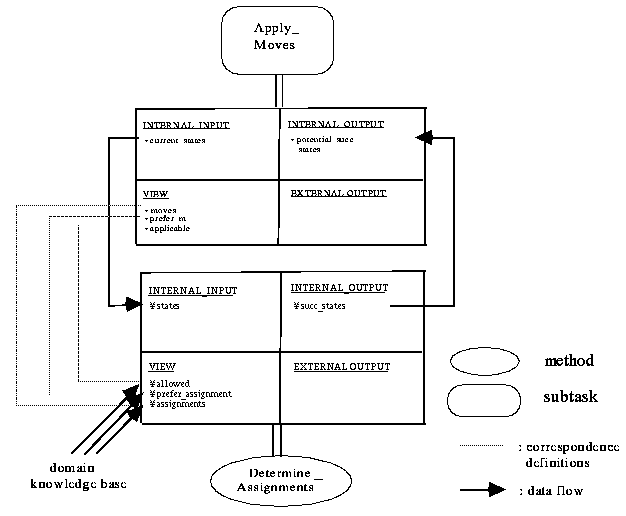
Figure 4-4: Ontology mapping between the subtask "Apply_Moves" and the
method "Determine_Assignments"
Let us now illustrate this notion of ontology mapping in the board-game method context (see Fig. 4-4). Since the external knowledge role "State" of "Determine_Assignments" is associated with the input store "Current_State" of the subtask "Apply_Move", there exists a downward mapping from the concept "current_states" to the concept "states". Correspondingly, we have an upward mapping from "succ_states" to "potential_succ_states", since the external knowledge role "Successor_States" of "Determine_Assignments" is associated with the output store "Potential_Successor_States" of "Apply_Moves"[2].
Furthermore, we assume that in the calling environment of the board-game method it has been decided that the external knowledge roles "Preferred_Moves", "Moves", and "Applic_Moves" should be handled as views. This decision is transferred to the subtask "Apply_Moves". Thus, all external input of the subtask is reinterpreted as view input (compare Fig. 3-7 and Fig. 4-4) (that is, in the current environment the knowledge about moves, preferences between moves and applicability of moves has to be taken from the domain).
These distinctions are in turn inherited by the selected submethod "Determine_Assignments". As a consequence, the global definitions of the method ontology of "Determine_Assignments" (see Fig. 4-1) are split up into an internal and an external section, where the external input section is again interpreted as view input - due to the decision made on the board-game method method level and due to the transfer of this decision to the subtask "Apply_Moves". Therefore, a correspondence, for instance, between the concept "moves" and the concept "assignments" is established. This means that the method "Determine_Assignments" has to access the domain knowledge in order to describe assignments and thus moves in domain-specific terms.
It should be clear that the subtask-to-method mapping of ontologies can be extended to multiple levels of mappings in a straightforward way. Decisions about the handling of external knowledge roles, which are made according to the calling environment of a method on level i are inherited by the subtasks of this method and further on by the (sub-)methods on level (i+1) that are selected to solve these subtasks. Our framework guarantees that domain knowledge is only accessed an the lowest level of the PSM configuration: thus any internal mapping of domain knowledge within the PSM configuration is avoided.
5. Discussion
When developing the approach several design decisions have been made.
A first decision was to introduce a single global method ontology. The advantage of that decision is that a method comes with a single ontology which is then - together with the domain ontology - the reference point for defining the application ontology (Gennari et al., 1994). On the other hand, from the notion of a (global) method ontology the need arises to establish internal mappings between the method, subtask, and submethod ontologies. However, without such a (global) method ontology, multiple sets of mappings between the application ontology and the various submethod ontologies would be required. In the end, we think that the proposed solution results in a clearer interface structure for a method, which is advantageous when handling a library of methods.
A second important aspect is the handling of the domain views of the method. The proposed approach supports a method interface that leaves open which knowledge is to be taken from the domain and which is delivered as input by the surrounding (sub-)task environment. In this way a method may be adapted in a very flexible way to its calling environment. On the other hand, one could also think of making this decision already within the method interface specification (that is, by using external stores and views/terminators instead of external knowledge roles). Thus, the specification of a method could clearly define which of its knowledge requirements have to be fulfilled by domain knowledge. It needs further experience in configuring methods to see which alternative works better in the end. However, the approach, as described in Section 4, makes fewer commitments within the method interface and thus leaves the way open to adopt the second alternative.
A third aspect we want to address is the handling of the multiple levels of mappings. An obvious disadvantage is the overhead which is created by these mappings. With respect to the development effort which is caused by the definition of all these mappings we will investigate in the future to which extent these mappings may be generated from the given ontologies. Concerning the runtime overhead we could think of a two-steps approach. During the process of configuring a method, the multiple levels of mappings provide a high flexibility in experimenting with different configurations: Replacing a submethod for solving a subtask by another submethod just requires the re-definition of the local mappings. As soon as the configuration of the method is stable, part of the multiple-level mappings may be compiled into more efficient mapping structures as part of the design and implementation activities. Thus the run-time overhead could be reduced. However, an investigation of such a compiling approach is a topic of future research.
The approach described in this paper is closely related to the notion of mapping relations (Gennari et al., 1994). Obviously, the type of mapping relations that have been defined in PROTÉGÉ-II (Gennari et al., 1994) are relevant in our framework as well. However, it is still open as to what additional types of mapping relations will be required in the end. Hopefully, some further insights may be gained from the database community and its investigation of schema transformations in the context of interoperable data bases (see e.g. (Hsiao et al., 1993)).
The aspects of configuring methods from more elementary components is investigated in several other approaches. The CommonKADS framework (Schreiber et al., 1994b) (Breuker and Van de Velde, 1994) bears a lot of similarities with the approach introduced in this paper. The decomposition of methods into subtasks as well as the notion of knowledge roles for describing the interface of (sub-)tasks directly corresponds to the CommonKADS framework. In CommonKADS this task interface is defined by so-called input/output roles (Schreiber et al., 1994a). In contrast to our approach, there is no notion of a subtask ontology and therefore no explicit description of ontology mappings within a configured method. Furthermore, the definition of the Conceptual Modelling Language (CML) (Schreiber et al., 1994a) does not specify explicitly how a problem solving method is applied to a task definition.
The DIDS-approach (Runkel et al., 1994) also provides means for building up problem solving methods from more elementary mechanisms. In DIDS a task description includes among others a specification of knowledge structures that define an ontology of the knowledge necessary for solving the task and operators that perform operations on these knowledge structures. Operators use such knowledge structures as input and produce modified structures as output. DIDS offers predefined mechanisms that realize these operators. Such an operator comes with a description of its input/output structures. Within the DIDS framework the "matching" of the operator input/output knowledge structures with the input/output structures of the mechanism is restricted to a one-to-one correspondence of the respective (knowledge) structures. This is in contrast to our approach that offers flexible mappings for relating subtask ontologies with corresponding method ontologies.
A further approach which provides means for configuring methods is the componential methodo-logy (ComMet) (Steels, 1993) (Gossens, 1995). Within ComMet feature structures are used to characterize components and to check the compatibility of components. However, ComMet does not introduce the notion of a method ontology and corresponding ontology mappings.
In the Spark, Burn, Firefighter framework (Yost et al., 1994), mappings are only discussed in the context of the active glossary, which relates the terminology of a workplace analysis with the terminology of appropriate problem-solving mechanisms (Klinker et al., 1993). On the one hand, the terms that are used to describe the input/output behavior of the activities which have been identified during the workplace analysis are related to the terms of the active glossary. On the other hand, the terms of the active glossary are related to the vocabulary of the reusable mechanisms. Based on this information mechanisms may be selected for solving a given activity. However, the framework does not offer means (i) for specifying more complex mappings and (ii) for a multi-level configuration of a complex method from more elementary meachanims.
6. Conclusion
In this paper, we have introduced a framework for handling method ontologies during the process of configuring methods. Characteristic features of the proposed approach are the definition of a single global method ontology and the notion of subtask ontologies. By introducing subtask ontologies the global ontology of a method is made independent from the ontologies of the submethods which are used to solve the subtasks. Thus a great amount of locality for the selected submethods is achieved. Furthermore, within the framework domain knowledge is only accessed by (sub-)methods on the lowest level of refinement. Thus, no mapping of domain knowledge between different configuration levels is required.
Of course, this approach for configuring various methods from more elementary submethods has to be evaluated by applying the framework for solving different application tasks. As one evaluation step we plan to specify and implement the board-game method according to the proposed framework.
The framework has been described rather informally in this paper. However, the framework can be formalized by using the new version of the Knowledge Acquisition and Representation Language KARL that is currently under development (Angele et al., 1996a). More specifically, all the ontology definitions for subtasks and methods as well as the required mappings can be directly specified in KARL. The framework that is described in this paper is supplemented with current research activities which investigate the formal specification of the functionality of (sub-)tasks and of problem solving methods (Fensel et al., 1996b). Results of these research activities will be used for addressing the indexing problem, that is for identifying the appropriate problem solving method for solving a (sub-)task at hand.
Acknowledgement
Fruitful discussions with Juergen Angele, Stefan Decker, Michael Erdmann, Rainer Perkuhn, and Yuval Shahar are gratefully acknowledged. Rainer Perkuhn provided valuable editorial support. The main parts of this framework have been worked out while the first author spent part of his sabbatical with the PROTÉGÉ-II group.
This work has been partially supported by a grant from Deutsche Forschungsgemeinschaft. This work has been supported in part by grant LM05208 from the National Library of Medicine, by gifts from Digital Equipment Coorperation, by grant dnr 93-3233 from the Swedish National Board for Industrial and Technical Development (NUTEK), and by scholarships from the Swedish Institute, from the Fulbright Commission, and from Stanford University. Dr. Musen is recipient of National Science Foundation Young Investigator Award IRI-9257578.
References
Angele, J., Decker, St., Perkuhn, R., and Studer, R. (1996a): Modeling problem-solving methods in new KARL. In Proc. of the 10th Banff Knowledge Acquisition for Knowledge-based Systems Workshop, Banff, Canada.
Angele, J., Fensel, D., and Studer, R. (1996b): Domain and task modeling in MIKE. In A.G. Sutcliffe et al., Eds. Domain Knowledge for Interactive System Design, Proc. IFIP WG 8.1/13.2. Joint Working Conf., Geneva, Chapman & Hall.
Breuker, J. and Van de Velde, W., Eds. (1994): CommonKADS Library for Expertise Modelling. IOS Press, Ohmsha.
Chandrasekaran, B. and Johnson, T. R. (1993): Generic tasks and task structures: history, critique and new directions. In J.-M. David et al., Eds. Second Generation Expert Systems, Springer-Verlag, Berlin.
Eriksson, H., Shahar, Y., Tu, S.W., Puerta, A.R., and Musen, M. (1995): Task modeling with reusable problem-solving methods. Artificial Intelligence, 79 (2), 293 - 326.
Fensel, D. (1995a): Assumptions and limitations of a problem solving method: a case study. In Proc. of the 9th Banff Knowledge Acquisition for Knowledge-Based Systems Workshop, Banff, Canada.
Fensel, D. (1995b): The Knowledge Acquisition and Representation Language KARL. Kluwer, Dordrecht.
Fensel, D., Angele, J., and Studer, R. (1996c): The Knowledge Acquisition and Representation Language KARL. IEEE Trans. on Knowledge and Data Engineering, to appear.
Fensel, D., Eriksson, H., Musen, M. A., and Studer, R. (1996a): Conceptual and formal specifications of problem-solving methods. Int. Journal of Expert Systems: Research and Applications, 1996.
Fensel, D., Schoenegge, A., Groenboom, R., and Wielinga, B. (1996b): Specification and verification of knowledge-based systems. In Proc. Workshop on Validation, Verification, and Refinement of Knowledge-Based Systems, 12th European Conf. on Artifical Intelligence (ECAI '96), Budapest.
Gennari, J. H., Tu, S. W., Rothenfluh, Th. E., and Musen, M. A. (1994): Mapping domains to methods in support of reuse. Int. J. of Human-Computer Studies, 41, 399-424.
Gossens, L. (1995): From ComMet to KresT. In Proc. of the 9th Banff Knowledge Acquisition for Knowledge-based Systems Workshop, Banff, Canada.
Hsiao, D., Neuhold, E.J., and Sacks-Davis, R., Eds. (1993): Interoperable Database Systems (DS-5), IFIP Transactions A-25, North-Holland, Amsterdam.
Klinker, G., Marques, D., and McDermott, J. (1993): The active glossary: taking integration seriously. Knowledge Acquisition, 5, 173-197.
Krueger, C. W. (1992): Software reuse. ACM Computing Surveys, 24 (2).
Linster, M., Ed. (1994): Sisyphus'91/92: Models of problem solving. Special Issue Int. Journal of Human Computer Studies, 40 (3).
McDermott, J. (1988): Preliminary steps toward a taxonomy of problem-solving methods. In S. Marcus, Ed. Automating Knowledge Acquisition for Expert Systems, Boston, MA: Kluwer.
Puerta, A. R., Edgar, J. W., Tu, S. W., and Musen, M. A. (1992): A multiple-method knowledge-acquisition shell for the automatic generation of knowledge-acquisition tools. Knowledge Acquisition, 4, 171-196.
Puppe, F. (1993): Systematic Introduction to Expert Systems: Knowledge Representation and Problem-Solving Methods, Springer-Verlag, Berlin.
Runkel, J. T., Birmingham, W. P., and Balkany, A. (1994): Separation of knowledge: a key to reusability. Proc. of the 8th Banff Knowledge Acquisition for Knowledge-based Systems Workshop, Banff, 1994.
Schreiber, G., Wielinga, B., and Breuker, J., Eds. (1993): KADS: A Principled Approach to Knowledge-Based System Development. Academic Press, London.
Schreiber, G., Wielinga, B., Akkermans, H., Van de Velde, W., and Anjewierden, A. (1994a): CML: The CommonKADS conceptual modeling language. In L. Steels et al., Eds. A Future for Knowledge Acquisition, Proc. 8th European Knowledge Acquisition Workshop (EKAW '94), Hoegaarden, Lecture Notes in AI, no. 867, Springer-Verlag, Berlin.
Schreiber, G., Wielinga, B., Akkermans, H., Van de Velde, W., and de Hoog, R. (1994b): CommonKADS. A comprehensive methodology for KBS development. IEEE Expert, 9 (6), December 1994.
Steels, L. (1993): The componential framework and its role in reusability. In J.-M. David et al., Eds. Second Generation Expert Systems. Springer Verlag, Berlin.
Yost, G. R., Klinker, G., Linster, M., Marques, D., and McDermott, J. (1994): The SBF framework, 1989 - 1994: From applications to workplaces. In L. Steels et al., Eds. A Future for Knowledge Acquisition, Proc. 8th European Knowledge Acquisition Workshop (EKAW '94), Hoegaarden, Lecture Notes in AI, no. 867, Springer-Verlag, Berlin.