Temporal Semantics of Complex Reasoning Tasks

• 1 INTRODUCTION
• 2 MODELLING REASONING BEHAVIOUR
  • 2.1 Task decomposition
  • 2.2 Information exchange between (sub-)tasks
  • 2.3 Task sequencing
  • 2.4 Role delegation
  • 2.5 Knowledge structures and relation to tasks
  • 2.6 Detailed specification
  • 2.7 Comparison to other approaches
• 3 TEMPORAL SEMANTICS OF REASONING BEHAVIOUR
• 4 COMPOSITIONAL INFORMATION STATES
• 5 COMPOSITIONAL BEHAVIOUR
  • 5.1 Transitions between components
  • 5.2. Transitions due to task control
  • 5.3. Compositional Transitions
• 6 DISCUSSION AND CONCLUSIONS
• ACKNOWLEDGEMENTS
• REFERENCES

1 INTRODUCTION

Complex tasks in which reasoning plays an important role, such as design and decision tasks, are most often extremely dynamic. The behaviour exhibited by (design and decision) systems is the result of interaction between (autonomous) agents and the material world. Non-monotonic behaviour is the rule rather than the exception.

The aim in knowledge engineering is to model such complex behaviour. The common approach is to model complex functionality by means of task (de)composition; where a complex task at a certain level comprises of subtasks and task control at a lower level. Non-monotonic behaviour modelled in this way naturally leads to a view of behaviour as sequences of states (of eventually monotonic subtasks) over time. A system, for example, can explicitly reason about its own behaviour on the basis of which it can influence its own control of its behaviour: in fact temporal reasoning.

Within knowledge engineering the ability to formally describe the behaviour of models (of complex tasks) contributes to the modelling, design, evaluation and maintenance, validation and verification, and reuse of components (of models of knowledge-based systems) (Harmelen and Fensel, 1995). As such, formal methods provide a means to formally describe a complex task thereby providing a common ground for informal models of the same complex task.

A framework that allows conceptual and formal specification of such models should be powerful enough to capture such behaviour in an explicit and transparant manner. A number of the current approaches to modelling complex reasoning tasks, in which formal specification plays an important role, are MIKE/KARL, KADS/(ML)², and MILORD (Fensel, 1993; Akkermans, Harmelen, Schreiber, and Wielinga, 1992; Agusti, Esteva, Carcia, Godo, de Mantaras, Murgui, Puyol, and Sierra, 1992; Fensel and Harmelen, 1994; Treur and Wetter, 1993). These frameworks include a formal syntax for the specification language, but the formal semantics of such systems from a temporal perspective is often not defined.

Especially for compositional dynamic tasks, both a conceptual and formal definition of the temporal semantics of behaviour is of importance. Formal semantics not only provides a basis for validation and verification of system behaviour, but specifications of components at different levels of abstraction with well-defined semantics also provide a means to enable automated support for redesign of task models and components (Brazier, Langen, Treur, and Wijngaards, 1996). Automated support for redesign, for example, often requires explicit formulation of requirements on system behaviour. In this paper the formal approach to modelling dynamic reasoning tasks within compositional architectures, DESIRE (Langevelde, Philipsen, and Treur, 1992; Brazier, Treur, Wijngaards, and Willems, 1995), and its temporal semantics is extended to include hierarchical decomposition.

Section 2 provides an overview of the knowledge modelled and specified in task models. In Section 3 the perspective on temporal semantics is introduced and the basic concepts are defined. In Section 4 definitions of the concepts required to formalise compositional information states are introduced, followed by definitions of concepts directly related to transitions between (hierarchical) component information states in Section 5. The formalisation of the resulting compositional behaviour is defined in terms of the temporal approach in Section 5 and discussed in Section 6. Further discussion of applications for which this approach has been successfully applied extends beyond the scope of this paper: see, for example (Brazier, Dunin-Keplicz, Jennings, and Treur, 1995; Brazier, Langen, Ruttkay, and Treur, 1994; Brazier and Treur, 1994; Geelen and Kowalczyk, 1992).

2 MODELLING REASONING BEHAVIOUR

A shared task model is, in fact, a mediating model. It mediates between a knowledge engineer and an expert, but also between a knowledge engineer and system design. Within the DESIRE framework task models provide the basis for system architecture. Tasks are mapped onto components, subtasks onto subcomponents, interactions between tasks are mapped onto information links between components. Domain knowledge is mapped onto structures which are referenced in specifications of components. The goals pursued and the roles of the parties involved in relation to the goals are defined. A description of the situation in which such goals can be pursued, and of the assumptions with respect to task performance are made explicit.

The result of task analysis is a conceptual specification of five types of knowledge:

• knowledge of task decomposition,
• knowledge of information exchange between (sub-)tasks,
• knowledge of task sequencing,
• knowledge of role delegation, and
• knowledge of knowledge structures and relation to tasks.

2.1 Task decomposition

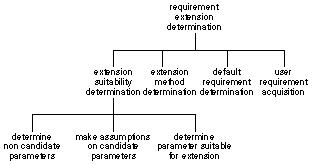
A task hierarchy defines which subtasks of the task are distinguished and the task-subtask relations between them. This entails a one-to-many relation which, for example, can be specified by means of a table (not shown) and depicted as a tree structure or a box-in-box structure (see Figures 1 and 2).

Figure 1: Pictoral specifications of a task decomposition.

In the task model for an elevator configuration task (Brazier, Langen, Treur, Wijngaards, and Willems, 1996), 'requirement extension determination' proposes extensions to the current set of requirement parameters. It proposes values for requirement parameters that do not have a value yet; adding this value extends the requirement parameters set. 'Extension suitability determination' determines which requirement parameters are best suited to be given a value. 'Extension method determination' decides which method to use to determine a value for the chosen requirement parameter: by means of default reasoning or user consultation. 'Default requirement determination' assigns a value to the chosen requirement parameter, and 'user requirement acquisition' obtains a value by interacting with the user, and assigns the value to the chosen parameter.

The task of 'extension suitability determination' is decomposed into three subtasks, of which the task 'determine non-candidate parameters' finds out which parameters are not a candidate for extension, the task 'make assumptions on candidate parameters' employs a closed-world-assumption to determine which candidate parameters are still eligible for extension, and the task 'determine parameter suitable for extension' selects one of these eligible parameters as suitable parameter. This example illustrates a non-monotonic task realized by a combination of monotonic subtasks. The task of 'extension suitability determination' is non-monotonic as it does not conserve its output when more input is available (not retracting already known input).

Conceptually, for each task, the types of information required as input or generated as output of a task should be specified. This can be done by defining names for information types (names chosen by the knowledge engineer and the expert(s)) and relations expressing how such information is related to a tasks' output and/or input. In a pictoral representation, each (sub)task can be annotated with information regarding the types of information of its input and output, for example, with input to the left and output to the right as shown in Figure 2.

Figure 2: Input & output types of information of task 'extension suitability determination'.

The reflective nature of tasks is another important element of the task decomposition that is emphasised in DESIRE. Essential for a transparant specification of a system is a clear distinction between object-level reasoning about some domain, from meta-level reasoning about the state and goals of a system. This object-meta distinction between tasks can be specified explicitly as an object-meta relation, an example is shown in Table 1.

Table 1. Object-meta distinction between tasks

2.2 Information exchange between (sub-)tasks

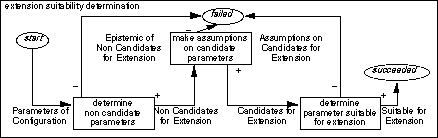
Figure 3: Information exchange among subtasks and between subtasks and the task of 'extension suitability determination'.

In Figure 3 examples of two kinds of relations are shown in a pictoral representation: private information exchange between the output information type of one subtask and the input information type of another subtask, and mediating information exchange between the output information type of a subtask and the output information type of its task (and vice versa).

Not only are the types of information to be transferred from one (sub-)task to the next (sub-)tasks defined, but also the grounds upon which the 'decision' to forward this information. Explicit evaluation criteria are specified for this purpose. They are discussed in next subsection.

2.3 Task sequencing

2.4 Role delegation

In complex situations often a number of autonomous systems and/or users are involved. Even in a traditional view of (knowledge-based) systems, the user and system interact to achieve the necessary behaviour. Knowledge of role delegation refers to the division of tasks amongst participants: minimally which tasks are to be performed by the system and which by one or more users. In more complex situations often more participants are involved. Essentially role delegation is defined by a set of participants (i.e. agents) and a relation between tasks and subsets of the set of agents. See Table 2 for an example.

Table 2: Role delegation of tasks of 'RQS Extension Determination'

A pictoral representation can be obtained by placing the (sets of) agents in the tree representing the task hierarchy.

2.5 Knowledge structures and relation to tasks

Knowledge of knowledge structures entails specification of the types of knowledge which are needed for task performance: for input and output information structures but also internal knowledge bases used for reasoning. For each task the names of information types and knowledge bases are related to the task(s) that refer(s) to them, as shown in an example below.

Table 3: Internal information type and knowledge base for subtasks of 'Extension Suitability Determination'

Information types can be defined in a compositional manner by combining them from sub information types. This can be specified by means of a relation defining a tree as is shown in Table 4.

Table 4: Hierarchy of information types.

Graphical representations can be made in tree or block form. The same can be done for knowledge bases, as is shown in Table 5.

Table 5: Hierarchy of knowledge bases

2.6 Detailed specification

Specification of a system is most often an iterative process: in time more detailed knowledge is acquired and modelled. The types of knowledge described during conceptual analysis have a (unique) counterpart in the specification. The types of knowledge become more explicit, and are defined more precisely.

Each task is mapped onto a component. Each component has a uniform structure (see Figure 5), that distinguishes between task control information and kernel information. The kernel information of a primitive (monotonic) component corresponds to a knowledge base, whereas the kernel of a composed (possibly non-monotonic) component consists of subcomponents and information links. The task control information of a primitive component consists of an inference engine, whereas the task control of a composed component consists of knowledge about task control. Another distinction made in the uniform structure is between public and private information, which fulfills the notion of information hiding.

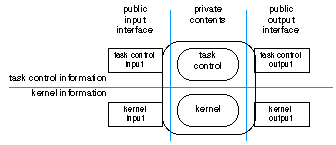
Figure 5: Uniform structure of a component.

During detailed specification (primitive) tasks are mapped onto (primitive) components, information exchange onto information links, and task sequencing knowledge onto task control knowledge. Moreover, the input, output and internal information types need to be mapped upon signatures (in our case: sets of ground atoms). This entails:

• extending the task decomposition to include references to the signatures required for input and output, and to include specifications of the meta/object distinctions.
• defining the information links between and within components at the level of the ground atoms.
• specifying the sequencing of component activation and the conditions under which components are to be activated.
• defining the information structures and knowledge to which the conceptual description referred: (object and/or meta-level) signatures for input and output, and knowledge bases for primitive components.

2.7 Comparison to other approaches

The formal specification framework DESIRE has been compared to other approaches. The formal specification language of DESIRE has been shown to be more flexible in modelling reasoning patterns (Harmelen and Fensel, 1995). In terms of expressive power, declarativeness, adequacy to specify dynamic aspects of reasoning patterns, possibility to specify multi-level architectures, adequacy to specify non-classical reasoning, executability and availability of formal semantics, the formal specification language within the DESIRE framework is to some extent comparable to other formal specification languages such as (ML)² (Akkermans, Harmelen, Schreiber, and Wielinga, 1992) and KARL (Fensel, 1993). It differs in that it is executable and can specify integrated systems. The formal specification languages languages differ in expressiveness of control knowledge (Treur and Wetter, 1993; Fensel and Harmelen, 1994).

Task control knowledge within DESIRE is located within each composed task (or component); i.e. distributed control. In (ML)² and KARL task control knowledge is expressed in a separate layer. Also the ability to perform reflective reasoning (both upward and downward reflection) is a major difference, enhancing DESIRE's flexibility in modelling reasoning patterns.

3 TEMPORAL SEMANTICS OF REASONING BEHAVIOUR

Behaviour is formalised as sequences of information states in which truth-values are assigned to elements describing the domain a component is reasoning about. The current state of a system is reflected by the current assignment of truth-values. The behaviour of a compositional architecture is mirrored in its successive (overall) information states, each defined by the composition of the information states of its sub-components.

The elements used to describe the states (the ground atoms) are expressed in a language that is defined by a signature. Each component within a compositional architecture has an information state describing the truth values (false (0), true (1) and undefined (u)) of atoms of the component.

Definition 3.1 (signature, information state) A signature is a structure of symbols defining a set of ground atoms At(). An information state for a signature is a mapping from the set of ground atoms At() to the set of truth values {0, 1, u}; i.e. a (partial) model M : At() {0, 1, u}. The set of all information states of signature is denoted by IS().

An example of a structure defining a signature is a tuple of (sub)sorts, constants, functions, and predicates of a many-sorted predicate logic, used in the DESIRE specification below, as is the use of referenced signatures for importing already defined signatures.

signature RequirementParameter_sig sorts RequirementParameter objects car_cab_height,..:RequirementParameter; end signature

signature NonCandidateReqParm_sig referenced signatures RequirementParameter_sig; relations non-candidate: RequirementParameter; end signature

The set of ground atoms defined for NonCandidateReqParm_sig is defined as follows:

Formalising information states as partial models is sufficient to model the reasoning behaviour of common inference mechanisms, such as chaining or unit-resolution, in terms of all ground literal conclusions that have been derived up to a certain moment in time.

Behaviour is the result of transitions from one information state to another. Transitions are defined within the compositional structure of the information states they manipulate: a transition only changes the information state in one of its components.

Definition 3.2 (transition) A transition between information states is a pair of partial models; i.e., an element {S, S'} (also denoted by S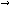S') of IS([Sigma]) x IS([Sigma]). A transition relation is a set of these transitions, i.e. a relation on IS() x IS().

If a transition relation is functional then it specifies deterministic behaviour. By applying transitions in succession, sequences of states are constructed. These sequences, also called traces (and interpreted as temporal models), formally describe behaviour. They adhere to the compositional structure: a trace describes a composed information state that develops in time (see Figure 6).

Definition 3.3 (trace and temporal model) A trace or partial temporal model of signature is a sequence of information states (M^t)_{t N} in IS(). The set of all partial temporal models is denoted by IS()^N, or Traces().

A set of partial temporal models is a declarative description of the semantics of the behaviour of the system; each temporal model can be seen as one of the alternatives for the intended behaviour.

Figure 6: Information states in time.

4 COMPOSITIONAL INFORMATION STATES

The execution of the corresponding task changes both the internal information state of the component (private information) and the output information made available to other components (public information). The private information is based on internal signatures and signatures of the public input and output; during execution inputs are taken from the input interface (input buffer) and outputs are transferred to the output interface (output buffer). The distinction between public and private information within a component is shown in Figure 5. Also the distinction between task (control) related information and kernel related information is shown in Figure 5.

Definition 4.1 (public kernel information) Each component C is assigned a signature, called the public kernel signature of C, denoted by _C,pub^ker. The input and output parts are subsignatures, denoted by _C,in^ker and _C,out^ker. The public kernel information state for C is the information state for signature _C,pub^ker and the fixed set of public kernel information states for C is denoted by IS_pub^ker(C).

Kernel information states can be either primitive or composed. The atoms which determine a primitive kernel information state are defined within the kernel of a primitive component (e.g., the signature of a knowledge base). The kernel information state of a composed component is a combination of the kernel information states for the component's subcomponents.

Definition 4.2 (kernel information state) Let D be a component.
a) If D is primitive, then its set of private kernel information states is defined by:

IS_pri^ker(D) = IS(_D,pri^ker)

IS_pri^ker(D) = _{C Ch(D)} IS^ker(C)

IS^ker(D) = IS_pri^ker(D) x IS_pub^ker(D)

An example of a composed information state is shown in Figure 9, where each of the columns is a composed information state.

The private part of the information state of the task control component can be constructed in a similar manner. The task control knowledge is used to supervise the activations of the kernel (both subcomponents and information links). Task control information includes specification of sets of goals and requests, exhaustiveness of search, etc: the additional information required to execute a task.

Definition 4.3 (task control information state) The task control of a component C is modelled as a component. Similar to definitions 4.1 and 4.2 an information state is defined.

a) For any component D the set of public task control information states is defined by:

IS_pub^tc(D) = IS(_D,pub^tc)

IS_pri^tc(D) = IS(_D,pri^tc)

IS^tc(I)

IS^tc(C) = IS_pub^tc(C) x IS_pri^tc(C)

IS^com,tc(D) = _{C C(D)} IS^tc(C) x _{I KL(D)} IS^tc(I)

IS^tc(D) = IS_pub^tc(D) x IS_pri^tc(D) x IS^com,tc(D)

The knowledge about the private task control is specified explicitly in DESIRE; the signatures used are generic (including relations such as next-state, next-uptodate-link, ...), see Section 5.2.

The kernel and the task control together define the information state of components.

Definition 4.4 (component information states) Let D be any component.

The set of information states of D is defined as:

IS(D) = IS^ker(D) x IS^tc(D)

Another distinction in the structure of the information state can be made. The kernel input and output interface are not merely a collection of signatures, but are viewed as a combination of signatures, where signatures are grouped in levels, and levels are ordered in an object/meta/meta-meta/...-relation.

In the context of compositional structures and for the specification of detailed process information the notion of levelled signatures is important. The specification of more detailed dynamics is modelled through (meta-level) reasoning of one level about the state of the process of the level below.

5 COMPOSITIONAL BEHAVIOUR

The notion of a transition relation can be generalised for the compositional case, defining a compositional transition relation. A binary relation is defined between a tuple of information states (left hand side, precondition of the transition) and another tuple of information states (right hand side, result of the transition). This transition relation between one part of a compositional state and another part of a compositional state induces a transition relation for the compositional state as a whole.

Transition relations exist both within and between components. An information state of a component can be changed either because a component has been active and generated new information itself, or because information has been transferred/exchanged from one component to another. Transitions between components are specified by information links as defined below. Transitions within components are either transitions within the kernel, transitions within the task control, or transitions between task control and the kernel.

5.1 Transitions between components

To enable information exchange between components, information links are specified: between two components (private links) or between (the interface of) a component and one of its subcomponents (a mediating link), as shown in Figure 7.

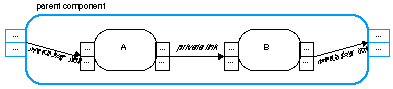
Figure 7: Kernel information links.

Information links are the logical basis for information exchange between components. It is assumed that the interface of every component consists of one or more (meta-)levels as explained above. Activations of a link from component C₁ to component C₂ causes a change in the information state of C₂ on the basis of information available in C₁. This change is a refinement or (for updates) a non-conservative modification of the information state of C₂. In effect it implies an extension, update or revision of the information state. A (relative) principle of conservation is assumed: all information that is not explicitly changed by an activation of a link will remain available (a specific frame assumption). The task control component controls the activation of the various links.

An information link is defined on the basis of semantic units: atoms and their truth values. In principle it relates a semantic unit of a component C₁, defined by a pair < a, tv₁ > of a ground atom a of one signature and a truth value tv₁ to a semantic unit of another component C₂, defined by a pair < b, tv₂> with b of another signature. Atoms which refer to the same entities in the world may be named differently within different components, in which case an information link defines the "translation" of atom names.

Definition 5.1 (semantic unit, kernel information link)

Let D be a complex component and C, C₁ and C₂ its subcomponents. The set of public semantic units of level x for the kernel of a component C is defined by

SU^(x)(C) = At(_C,pub^ker,(x)) x {0, 1, u}

a) A private kernel link of D, I from level x of C₁ to level y of C₂ is a binary relation

I : SU^(x)_out(C₁) x SU^(y)_in(C₂)

I : SU^(x)_in(D) x SU^(y)_in(C)
I : SU^(x)_out(C) x SU^(y)_out(D) and
I : SU^(x)_in(D) x SU^(y)_out(D)

A trivial standard example of an information link is when the sets of semantic units have a common subset U, and for < a, tv₁ > SU^(x)_out(C₁), < b, tv₂ > SU^(y)_in(C₂) the identity relation I is defined by I(< a, tv₁ >, < b, tv₂ >) if < a, tv₁ > = < b, tv₂ > U. Note that by restricting this subset U restricted information exchange is specified.

In the example below, the name of the parameter to be deduced is passed to the component that deduces an additional value. The transfer specified by a mediating link translates poss_ass( likely_candidate( X: RequirementParameter ) ) to candidate( X: RequirementParameter ).

  private link pass_to_deduce_reqparm: object-assumption
    domain make_assumption_on_candidate_parameter
      output output_1
    co-domain determine_parameter_suitable_for_extension
      input input_2
    sort links
      (RequirementParameter, RequirementParameter)
      (Value, Value )
    object links identity
    term links identity

    atom links

      (poss_ass( likely_candidate(P: RequirementParameter)),
        assumption(candidate( P: RequirementParameter), positive)):
        <<true, true>, <false, false>, <unknown. false> >;
   end link

: (A x B)x(B x C) with (< a, b >, < b', c' >)

that is *(< a, b, c >, < a', b', c' >) with a' = a
whenever (< a, b >, < b', c' >)

Definition 5.2 (information link transition) Suppose E₁ and E₂ are components and I is a information link from level x of E₁ to level y of E₂.
A transition relation for the information link I is a relation

: (IS_x(E₁)xIS_y(E₂) x IS^tc(I)) x (IS_y(E₂)xIS^tc(I))

M'₂(b) = M₂(b) (conserved) or

I(< a, M₁(a) >, < b, M'₂(b)>) for some atom a (changed by the link)

5.2. Transitions due to task control

  task control extension_suitability_determination
    task control knowledge
      if start
        and target-set( determine_suitable_parameter)
        then next-state( determine_non_candidate_parameter, active)
        and next-target-set( determine_non_candidate_parameter, determine)
        and next-uptodate-link( a1 );
      .......
      if evaluation( determine_parameter_suitable_for_extension, det_suit_param, succeeded, any )
        then stop
        and next-uptodate-link( pass_suitable_parameters_to_output );
      ........
  end task control

Definition 5.3 (task control transition) A task control transition relation for a component C is a relation associating task control information states for C to task control information states for C; i.e., a relation : IS^tc(C) x IS^tc(C) where each transition is induced by the task control specification.

The task control information must, in some way, be transferred between the task control of the parent component and the task control information of the subcomponents. Three kinds of task control links are discerned: upward task control links, and downward task control links that connect the private task control to the subcomponent and sublink task control, and thirdly the mediating task control links that communicate the private task control to the public task control and vice versa (see Figure 8).

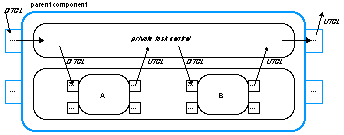
Figure 8: Task control links

Formally, task control links are defined as follows. For example, each component C has a downward link defined by the pair < next-state(C, active), 1 >, < state(active), 1 >.

Definition 5.4 (task control link) Let D be a composed component and let the set of semantic units SU_pri^tc be defined by SU_pri^tc(D) = At(_D,pri^tc) x {0, 1, u}.

a) A (combined) downward task control link (denoted by DTCL) is a set consisting, for each subcomponent C, of a relation on

I : SU_pri^tc(D) x SU_in^tc(C)
where SU_in^tc is defined by SU_in^tc(C) = At(_C,pub^tc) x {0, 1, u}

I : SU_out^tc(C) x SU_pri^tc(D)
where SU_out^tc is defined by SU_out^tc(C) = At(_C,pub^tc) x {0, 1, u}

I : SU_in^tc(D) x SU_pri^tc(D) or I : SU_pri^tc(D) x SU_out^tc(D)

Definition 5.5 (task control link transition) Let D be a complex component.

a) A transition relation for the upward task control link UTCL is defined as a relation

_UTCL : (IS^com,tc(D) x IS^tc(D)) x IS^tc(D)

N'₂(b) = N₂(b) (conserved) or
I(< a, N₁(a) >, < b, N'₂(b)>) for some atom a (changed by a link).

_DTCL : (IS^tc(D) x IS^com,tc(D)) x IS^com,tc(D)

N'₂(b) = N₂(b) (conserved) or
I(< a, N₁(a) >, < b, N'₂(b)>) for some atom a (changed by a link).

5.3. Compositional Transitions

For primitive reasoning components, kernel transitions are induced by inferences on the basis of knowledge in the knowledge base. Compositional transitions define the dynamic semantics of hierarchical compositional systems.

Definition 5.6 (kernel transitions) Let C be a component. A kernel transition relation for a component C (or private component transition relation) is a relation associating information states for C to information states for C; i.e., a relation

: IS^ker(C) x IS^ker(C)

Definition 5.7 (compositional transitions) Let D be a composed component with subcomponent C. A compositional transition relation for the D is a transition relation

: IS_pri(D) x IS_pri(D)

(1) a kernel transition, (2) a task control link transition, (3) a task control transition.

The following definition shows how traces generated by iteratively applying a transition function on the current information state can be interpreted as temporal models giving a declarative description of the semantics of the behaviour of the system; they can be viewed as the intended (behavioural) models of the system.

Figure 9: A trace of information states.

Definition 5.8 (compositional trace) Let D be a component.

a) A trace of a component D is a sequence of information states (M^t)_{t N} in IS^com(D). The set of all traces is denoted by IS(D)^N, or Traces(D).

b) An element (M^t)_{t N} Traces(D) is called a temporal model of D if for all time points t the step from M^t to M^t+1 is defined in accordance with a compositional transition of the system. The set of temporal models of D forms a subset BehMod(D) of Traces(D).

A temporal model describes a trace representing possible (intended) behaviour of the reasoning. One view is that the trace is generated by the (execution of) transition functions, given initial input information. From every initial information setting a trace can be generated by the transitions. Together the generated traces form the set BehMod(D). A slightly different view is that the transition relations define a set of (temporal) axioms or constraints BehTheory(D) on temporal models in Traces(D). The possible behavioural alternatives are given by the set of the temporal models satisfying these temporal constraints:

TempMod(D) = { M Traces(D) | M BehTheory(D) }

6 DISCUSSION AND CONCLUSIONS

Another formal specification language that supports hierarchical task structures is KARL (Fensel, 1993) in which inference actions can be defined in terms of other (more primitive) inference actions. This language is related to the KADS methodology (Schreiber, Wielinga, and Breuker, 1993) with its three independent (hierarchically organised) layers. In KADS, hierarchical decomposition is only available at the task layer. The introduction of hierarchical decomposition at the inference layer in KARL is an extension of KADS. In KARL the decomposition of the inference layer is in a one to one correspondence to the decomposition of the task layer. Similar to the approach here the semantics attributed to a composed inference action takes into account the related control structure at the task layer and the primitive inference actions included. A difference with our approach is that in our specification this related control structure is included in the composed component itself and not separated at a distinct (task) layer. This implies that in our case the specification document mirrors the compositional structure more explicitly, in the sense of 'hiding' the control inside the composed component. Moreover, in KARL the temporal aspects are not explicitly covered by the formal semantics that assigns a 'static' (input-output) semantics to the inference layer independently from the task layer. A conclusion from our work presented here is that control and temporal semantics are necessarily intertwined for models of complex (non-monotonic) tasks.

In particular, for applications in which the interaction between components that reason and act autonomously, such as cooperative (human-computer) systems and multi-agent systems, the dynamics of interactions is crucial. These interactions take place in a dynamically controlled manner and can be modelled in our temporal framework by transitions between states. As KADS is based on a different conceptual model (the four layer model), in which the notions of state and transition are left implicit, KADS languages like KARL and (ML)² have difficulty expressing dynamically controlled interactions between autonomous components in an adequate manner.

A formal basis to the conceptual phase of complex system design, supporting knowledge acquisition and within which behaviour can be explicitly modelled, is available. Reuse of formally specified (sub)components of a system is possible. The behaviour of the (sub)components in interaction with other (sub)components can be well-defined. In current research multi-agent situations, in which agents are modelled as interacting components, are being explored. Given compositional descriptions of complex dynamic systems, together with well-defined semantics, validation and verification of system behaviour should be possible. Initial research in this area is promising (Treur and Willems, 1995). Within the context of the approach described, further foundational research with respect to modelling complex reasoning can be investigated: more intricate patterns of reasoning behaviour can be explored and formally described.

ACKNOWLEDGEMENTS

This research was partly funded by the Netherlands Organization for Scientific Research (NWO) within the REVISE project "Evolutionary design in knowledge-based systems" (project number 612-322-316) and the ESPRIT III Basic Research project 6156 DRUMS II.

REFERENCES

Agusti, J., Esteva, F., Carcia, P., Godo, L., Lopez de Mantaras, R., Murgui, Ll., Puyol, J., and Sierra, C. (1992). Structured Local Fuzzy Logics in MILORD, In: Zadeh, L., and Kacprzyk, J. (Eds.) Fuzzy Logic for the Management of Uncertainty, John Wiley & Sons, Inc.

Akkermans, J.M., Harmelen, F. van, Schreiber, A.Th., and Wielinga, B.J. (1992). A formalisation of knowledge-level models for knowledge acquisition. Int. J. Of Intelligent Systems.

Blamey, S. (1986). Partial Logic. In: D. Gabbay and F. Günthner (Eds.), Handbook of Philosophical Logic. Vol. III, pp. 1-70, Reidel, Dordrecht.

Brazier, F.M.T., Dunin-Keplicz, B., Jennings, N., and Treur, J. (1995). Formal Specification of Multi-Agent Systems: a Real-World Case, Proceedings First International Conference on Multi-Agent Systems, ICMAS'95, pp. 25-32.

Brazier, F.M.T., Langen, P.H.G. van, Ruttkay, Zs. and Treur, J. (1994). On the formalisation of design processes. In: Gero, J.S. (Ed.), AI in Design, Proceedings AID'94, Kluwer Academic Publishers, Dordrecht, pp. 535-552.

Brazier, F.M.T., Langen, P.H.G. van, Treur, J., Wijngaards, N.J.E. and Willems, M. (1996). DESIRE: Designing an elevator configuration. In: Schreiber, A.Th., and Birmingham, W.P. (Eds.), Special Issue on Sisyphus-VT. International Journal of Human-Computer Studies, 1996, Volume 44, pp. 469-520.

Brazier, F.M.T., and Treur, J. (1994). User centered knowledge-based system design: a formal modelling approach. In: Steels, L., Schreiber G. and Velde, W. van de (Eds.), A Future for Knowledge Acquisition, EKAW'94, Proceedings, Springer-Verlag, Dordrecht, pp. 283-302.

Brazier, F.M.T., Treur, J. and Wijngaards, N.J.E. (1996). The acquisition of a shared task model. In: Shadbolt, N., O'Hara, K., and Schreiber, A.Th. (Eds.). Advances in Knowledge Acquisition; 9th European Knowledge Acquisition Workshop, EKAW'96, Lecture Notes in Artificial Intelligence, Volume 1076, Springer Verlag, pp. 278-289.

Brazier, F.M.T., Treur, J., Wijngaards, N.J.E., and Willems, M. (1995). Formal specification of hierarchically (de)composed tasks. In Gaines, B.R. and Musen, M.A. (Eds.), Proceedings of the 9th Banff Knowledge Acquisition for Knowledge-Based Systems Workshop, KAW '95, Volume 2, pp. 25/1-25/20. Calgary: SRDG Publications, Department of Computer Science, University of Calgary.

Engelfriet, J. and Treur, J. (1994). Temporal theories of reasoning. In: MacNish, C., Pearce, D., and Pereira, L.M. (Eds.), Logics in Artificial Intelligence, Proceedings of the 4th European Workshop on Logics in Artificial Inteligence, JELIA'94, Springer-Verlag, volume 838 of Lecture Notes in Artificial Intelligence, pages 279-299.

Fensel, D. (1993) The knowledge acquisition and representation language KARL, PhD. Thesis, Univ. of Karlsruhe.

Fensel, D., Harmelen, F. van, (1994) A comparison of languages which operationalize and formalize KADS models of expertise. Knowledge Engineering Review, Volume 9, pp. 105-146.

Gavrila, I.S. and Treur, J. (1994). A formal model for the dynamics of compositional reasoning systems, in Cohn, A.G. (Ed.), Proc. 11th European Conference on Artificial Intelligence, ECAI'94 , John Wiley & Sons, Chichester, pp. 307-311.

Geelen, P.A., and Kowalczyk, W. (1992) A knowledge-based system for ruting of international blanc payment orders, In: Proc. of Int. Conf. on AI, Expert Systems and Natural Language, Avignon-92, vol 2, pp. 669-677.

Harmelen, F. van, and Fensel, D. (1995). Formal methods in knowledge engineering. The Knowledge Engineering Review, Volume 10(4), pp. 345-360.

Langevelde, I.A. van, Philipsen, A.W. and Treur, J. (1992). Formal specification of compositional architectures. In: Neumann, B. (Ed.), Proc. 10th European Conference on Artificial Intelligence, ECAI'92, John Wiley & Sons, Chichester, pp. 272-276. Extended version: Report IR-282, Vrije Universiteit Amsterdam, Department of Mathematics and Computer Science, 1991

Langen, P.H.G. van, and Treur, J. (1989). Representing World Situations and Information States by Many-Sorted Partial Models. Technical Report PE8904, University of Amsterdam, Department of Mathematics and Computer Science.

Langholm, T. (1988). Partiality, Truth and Persistence. CSLI Lecture Notes, No. 15. Stanford University, Stanford.

Schreiber, A.Th., Wielinga, B.J. and Breuker, J.A. (Eds.) (1993). KADS: A Principled Approach to Knowledge-Based System Development. Academic Press, London.

Treur, J. (1994), Temporal Semantics of Meta-level Architectures for the Control of Reasoning, In: Turini, F. (Ed.), Lecture Notes in Comp. Sc. 883, Springer-Verlag.

Treur, J. and Wetter, Th. (Eds.) (1993). Formal Specification of Complex Reasoning Systems, Ellis Horwood.

Treur, J. and Willlems M (1995). On verification in compositional knowledge-based systems. In: Rousset, M.-C. and Ayel, M. (Eds.), Proceedings European Symposium on Validation and Verfication on KBSes, EUROVAV'95, Chambéry.