Mildred L.G. Shaw and Brian R. Gaines
Knowledge
Science Institute
University of Calgary
Alberta, Canada T2N
1N4
mildred@cpsc.ucalgary.ca, gaines@cpsc.ucalgary.ca
The repertory grid has proved a useful tool for knowledge elicitation, yet its `flat' entity-attribute-value-value structure seems to preclude its use in developing the hierarchical knowledge structures common in semantic networks. However, it is known that general knowledge representation schemes, such as those of KL-ONE type systems, can be represented as an entity--attribute-value matrix in which the entities are concepts and the values are constraints. WebGrid-II extends the values available in a grid to include symbolic and numeric constraints, and this article demonstrates how various forms of grid analyses generate hierarchical knowledge structures from extended grids.
The Kelly repertory grid provides a simple matrix representation in which the set of integers is used for single-valued fillers (Kelly, 1955; Shaw, 1980). This limits its representation capabilities and a variety of extensions have been implemented or proposed (Boose and Bradshaw, 1987; Bradshaw, Ford, Adams-Webber and Boose, 1993; Gaines and Shaw, 1993). A major objective in our WebGrid development is to extend the forms of constraint that can be represented in a grid in order to increase its representational power, while retaining a simple user interface to the tool in order to maintain its usability. WebGrid-II provides categorical and numerical data types in addition to rating scales, and also allows symbolic values such as "any", "none", and "not applicable".
Gaines (1993, 1994) has developed a complete semantics for CLASSIC and similar KL-ONE derivatives in terms of a matrix in which the basic constraints are derived from set-theoretic constraints upon a filler set for a given role. An entity-attribute-value grid with the `values' extended to include more general constraints can emulate general concept-role-constraint knowledge representation systems, and it should be possible for the analysis of the grid to exhibit the underlying hierarchies in these structures. The following examples demonstrate that this is feasible in practice and a solid foundation for knowledge acquisition and modeling by showing how WebGrid-II with extended data types can be used to develop hierarchical data structures from nominally flat grids.
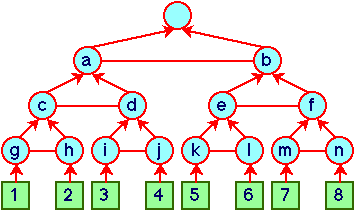
Consider a simple hierarchy with 8 leaf nodes based on 7 binary distinctions as shown in Figure 1. The symbolism of Figure 1 is that of the visual language KDraw (Gaines, 1991), which also corresponds to Kelly's hierarchical systems of bipolar constructs (Gaines and Shaw, 1993).

Figure 1 Basic hierarchy
A repertory grid was developed using as elements the 8 individuals shown at the bottom of Figure 1 and as constructs the 7 bipolar constructs distinguishing them. The FOCUS cluster analysis in WebGrid-II was used to analyze this grid producing the output shown in Figure 2. It can be seen that the element cluster at the bottom right of Figure 2 accurately reproduces the hierarchy of Figure 1. This can also be derived analytically as a general result for any size of hierarchy. Thus a FOCUS cluster analysis is a sound tool for deriving a hierarchical structure underlying a flat grid.
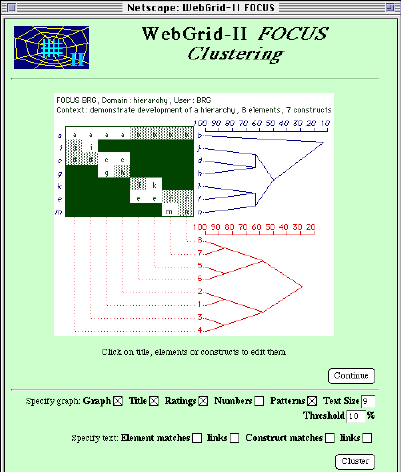
Figure 2 FOCUS reconstructing the hierarchy
As a more complex empirical example consider the concept map of Figure 3 which illustrates the relations between Internet services in terms of a set of basic distinctions (Gaines, Chen and Shaw, 1997).
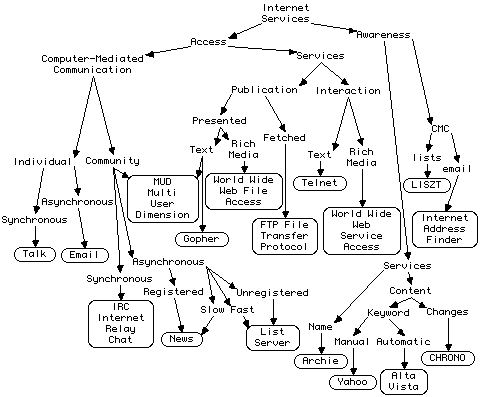
Figure 3 Hierarchy of Internet Services (Gaines et al., 1997)
When the data of Figure 3 is entered into WebGrid-II and a FOCUS cluster analysis is run the element tree generated is that shown in Figure 4. Again the hierarchical concept map is shown to be derivable from the flat grid.
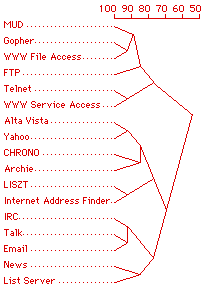
Figure 4 FOCUS reconstructing Internet hierarchy
Another way in which hierarchical structures may be developed in WebGrid is through the derivation of rules. This will be exemplified by an example that shows WebGrid in action. Figure 5 shows the initial screen of WebGrid-II. The HTML form requests the usual data required to initiate grid elicitation: user name; domain and context; terms for elements and constructs; default rating scale; data types allowed; and a list of initial elements. It also allows the subsequent screens to be customized with an HTML specification of a header and trailer--this capability to include links to multimedia web data is also used to allow annotation, text and pictures, to be attached to elements. The small "?" icons give access to context-sensitive on-line help.
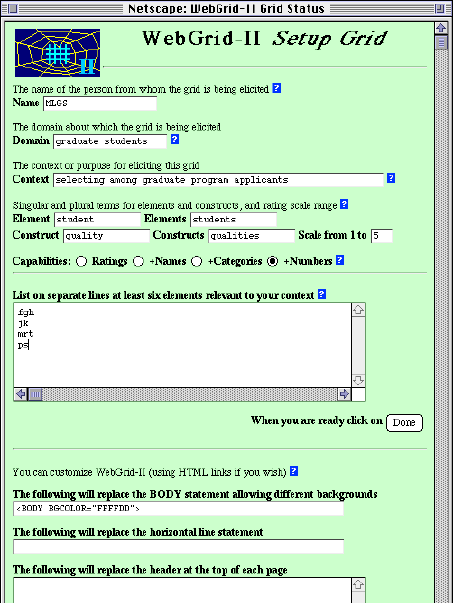
Figure 5 WebGrid-II initial screen
The problem domain is that of "selecting among graduate program applicants" and the intention of the user is to develop a set of rules defining the criteria for selection. The system will incorporate the text typed in by the user into the later dialog, and the user has stated that the elements in the grid are to be called "students" and the constructs "qualities." The user has set the types of constructs to be "Ratings+Names+Categories+Numbers"--the "Ratings" option elicits a standard repertory grid, the "+Names" option indicates that the user wants to use more advanced facilities for knowledge modeling, the "+Categories" allows categorical constructs to be defined, and the "+Numbers" option allows numeric constructs to be defined. She has left the default rating scale to be 1-5 and has entered the initials of 4 students typifying the range of selection decisions normally made.
When the user clicks on the "Done" button at the bottom, the browser transmits the data entered to the remote server which passes it through its common gateway interface to a specialist knowledge acquisition auxiliary server. The server processes the data and generates an HTML document that it returns to the browser resulting in the screen shown in Figure 6 eliciting a construct from a triad of elements.
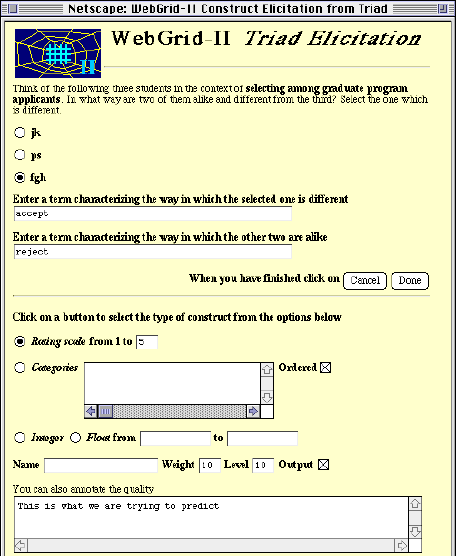
Figure 6 Construct elicitation from a triad
The upper part of the screen assumes that a rating scale will be used. The lower part of the screen is generated because advanced features were selected through the "+Numbers" option. It allows the user to vary the rating scale for an individual construct, to select a categorical, integer or float construct, to name the construct, to give it a weight in clustering, a priority level in asking questions in an expert system application, and to specify that the construct is an input for decision making purposes or an output to be anticipated. Since the construct entered is the main decision to be made, to accept or reject a student, and the user wants the system to anticipate the correct decision from the way the student is construed she has made it an output.
The user clicks on a radio button to select an element which she construes as different from the other two and enters terms characterizing the construct. When the user clicks on "Done" the server generates the screen shown on the left of Figure 7 which places a popup menu rating scale alongside each element enabling the user to rate each one along the new construct as shown on the right. She is also able to change the terms used if they seem inappropriate in the context of all the elements, and to change the ratings of the already entered elements if appropriate.
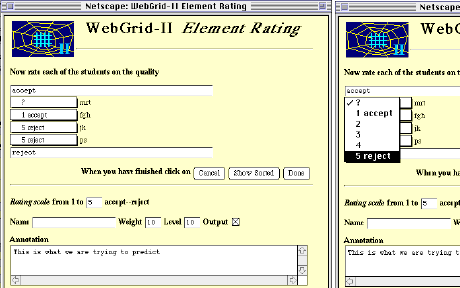
Figure 7 Rating elements on constructs
Clicking on the "Done" button in Figure 7 sends the ratings back to the server which generates the status screen shown in Figure 8.
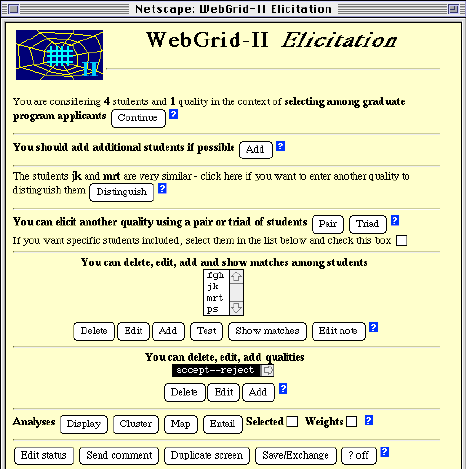
Figure 8 Status screen
This shows the elements and constructs entered, allowing them to be selected for deletion, editing and so on. It also offers various suggestions as how to continue the elicitation based on the data entered so far, facilities for analysis, saving the grid, and so on. The user decides to develop another two constructs from triads of elements and enters "high gpa--inadequate gpa" and "good references--inadequate references" since she knows that these are critical to acceptance.
The user notes that the students' grade point average (gpa) is important in admission decisions and click on "Add" under the list of constructs to add it. She fills in the screen shown in Figure 9, entering a construct called "gpa" which is a floating point number between 0 and 4. She uses the "Categories" box to define some categories based on gpa values, that 0 through 2.99 is inadequate, 3 through 4 is adequate and 3.5 through 4 is high.
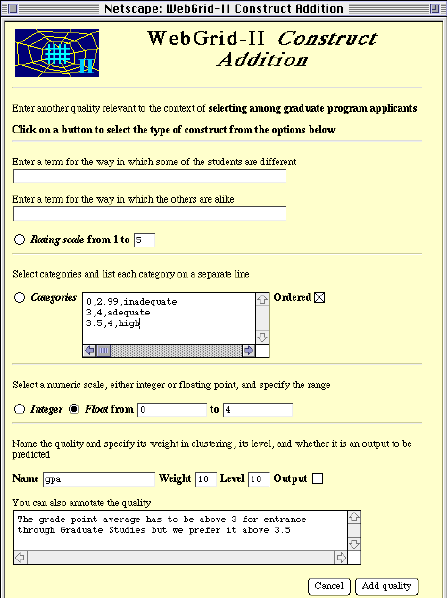
Figure 9 Defining a numeric construct
When she clicks on "Add quality" WebGrid-II returns the screen shown in Figure 10 asking her to enter numeric values for the gpa of each student.
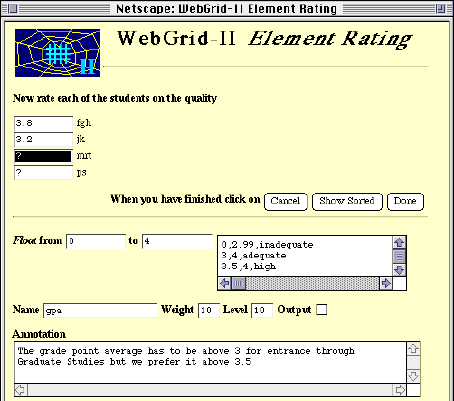
Figure 10 Entering numeric values
She enters another construct, "good references--inadequate references", and decides to run rule entailment to see if the constructs enter account for the admission decisions. This generates the screen of Figure 11 which shows that "ps" might have been expected to be admitted but was not. She realizes this is because he did not having anyone willing to supervise him, enters the construct "willing supervisor--no supervisor", runs rule entailment again and this time gets rules that correctly predict all 4 cases.
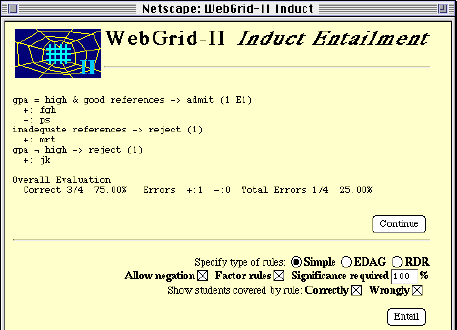
Figure 11 Rules entailed after 3 constructs
She then decides to check the rule against some more test cases and clicks on the "Test" button under the elements list in Figure 8. WebGrid-II generates the screen shown in Figure 12 which enables her to enter data on a test case and infer a conclusion from the rules.
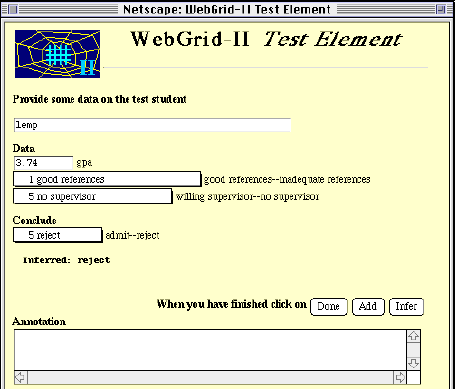
Figure 12 Inference with a test case
When she enters a student "lemp" WebGrid-II infers that he should be rejected but she remembers he was accepted because he had a scholarship and it was expected he would be easily able to find a supervisor. She clicks on "Add" to add this case to the grid and then adds the construct "has scholarship--no scholarship". She goes on adding cases and constructs using the test facility, the suggestions about matches on the main screen, and so on, until she has developed a grid of 12 elements and 7 constructs which results in the rules shown in Figure 13.
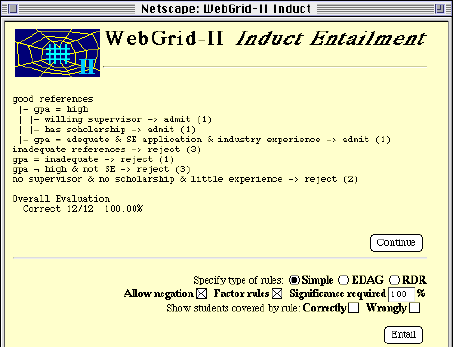
Figure 13 Final rules
The rule for admission is that the candidate must have good references and either a high gpa with a willing supervisor or a scholarship, or must have an adequate gpa and be applying for the software engineering specialization which also requires significant industry experience. She decides also to look at rules with exceptions, selects the "EDAG" button in Figure 13 and clicks on "Infer" to generate the screen of Figure 14. This says that a candidate should be rejected unless they have good references and in addition their gpa is high but they do not have no supervisor or no scholarship, or their gpa is adequate, they are applying for the SE specialization and have industrial experience.
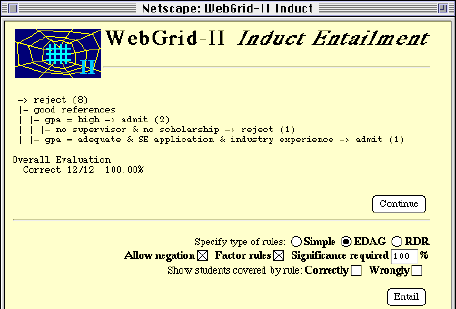
Figure 14 Final rules with exceptions
It can be seen in both Figure 13 and 14 that the induction of rules has itself generated a hierarchical conceptual structure. This is evident when the rule is represented as an EDAG in KDraw as shown in Figure 15. The rules generated from the flat grid result in an elaborate hierarchical conceptual structure.
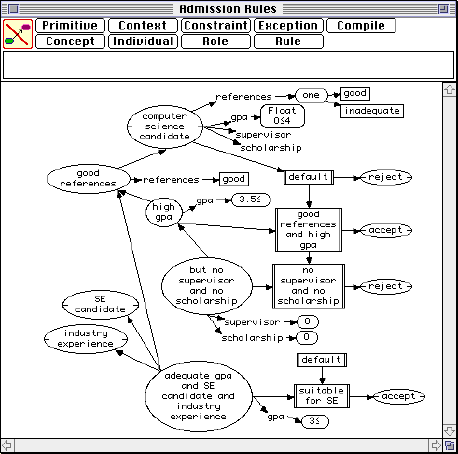
Figure 15 Final rules with exceptions in KDraw
Gaines and Shaw (1994) present a study of using knowledge acquisition and representation tools to support scientific communities in which they use a laddering technique to analyze the definition of an "IMS ideal artifact" in a paper by Tomiyama (1992) that defines the objectives of the international Intelligent Manufacturing Systems project. The analysis is presented as a knowledge structure in KDraw in Figure 16. The knowledge structure shows an IMS ideal artifact as being defined by its inheritance of 3 essential qualities, each of which is itself defined by its inheritance of 3 essential qualities. The qualities are themselves defined in terms of bipolar constructs consisting of pairs of disjoint primitives.
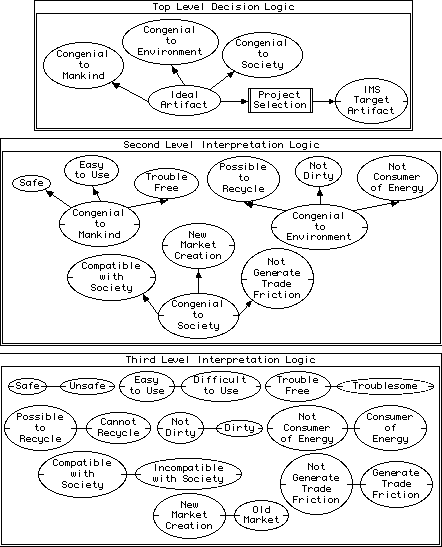
Figure 16 Tomiyama's definition of an "IMS Ideal artifact" represented in KDraw
It is possible to reconstruct this knowledge structure in WebGrid-II by entering a grid of 10 elements and 13 constructs where the elements are an instance of an ideal artifact together with the 9 near-misses that fail to be an ideal artifact by having one inappropriate value. The 4 derived constructs in the first level of Figure 16 are specified as outputs and running rule entailment in WebGrid-II derives their relation to one another and to the operational constructs as shown in Figure 17.

Figure 17 Rule entailment for a grid representing an ideal case and near misses for Fig.16
The rules derived in Figure 17 are a backward-chaining set reproducing the knowledge structure of Figure 16. When they are run on a test case, as shown in Figure 18, all four of the output constructs are derived allowing the reasons to be seen as to why a specific case is, or is not, an IMS ideal artifact to be seen--that is, the "why" or "why not" question is automatically answered in terms of the sub-goals.
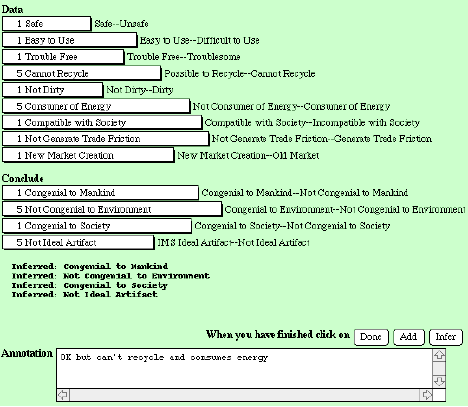
Figure 18 Testing a case as a potential IMS ideal artifact
The repertory grid has proved a useful tool for knowledge elicitation, yet its `flat' entity-attribute-value value seems to preclude its use in developing the hierarchical knowledge structures common in semantic networks. However, it is known that general knowledge representation schemes, such as those of KL-ONE type systems, can be represented as an entity--attribute-value matrix in which the entities are concepts and the values are constraints. WebGrid-II extends the values available in a grid to include symbolic and numeric constraints, and this article has demonstrated how various forms of grid analyses generate hierarchical knowledge structures from extended grids.
The first example shows how a typical conceptual hierarchy is perfectly reconstructed through the FOCUS cluster analysis, and how this applies to real data. The second example shows how a complex hierarchical structure naturally develops through the rules entailed by the grid. The third example shows how a typical conceptual hierarchy is perfectly reconstructed through the entailment of backward-chaining rules.
It is hoped that this article exemplifies the relationship between the flat structures of a repertory grid and the hierarchical structures of a semantic network in such a way as to suggest ways in which WebGrid-II might be integrated with various ontology tools.
Financial assistance for this work has been made available by the Natural Sciences and Engineering Research Council of Canada.
Boose, J.H. and Bradshaw, J.M. (1987). Expertise transfer and complex problems: using AQUINAS as a knowledge acquisition workbench for knowledge-based systems. International Journal of Man-Machine Studies 26 3-28.
Bradshaw, J.M., Ford, K.M., Adams-Webber, J.R. and Boose, J.H. (1993). Beyond the repertory grid: new approaches to constructivist knowledge acquisition tool development. International Journal of Intelligent Systems 8(2) 287-33.
Gaines, B.R. (1991). An interactive visual language for term subsumption visual languages. IJCAI'91: Proceedings of the Twelfth International Joint Conference on Artificial Intelligence. pp.817-823. San Mateo, California, Morgan Kaufmann.
Gaines, B.R. (1993). A class library implementation of a principled open architecture knowledge representation server with plug-in data types. IJCAI'93: Proceedings of the Thirteenth International Joint Conference on Artificial Intelligence. pp.504-509. San Mateo, California, Morgan Kaufmann.
Gaines, B.R. (1994). Class library implementation of an open architecture knowledge support system. International Journal Human-Computer Studies 41(1/2) 59-107.
Gaines, B.R., Chen, L.L.-J. and Shaw, M.L.G. (1997). Modeling the human factors of scholarly communities supported through the Internet and World Wide Web. Journal American Society Information Science 48(11) 987-1003.
Gaines, B.R. and Shaw, M.L.G. (1993). Basing knowledge acquisition tools in personal construct psychology. Knowledge Engineering Review 8(1) 49-85.
Gaines, B.R. and Shaw, M.L.G. (1994). Using knowledge acquisition and representation tools to support scientific communities. AAAI'94: Proceedings of the Twelfth National Conference on Artificial Intelligence. pp.707-714. Menlo Park, California, AAAI Press/MIT Press.
Kelly, G.A. (1955). The Psychology of Personal Constructs. New York, Norton.
Shaw, M.L.G. (1980). On Becoming A Personal Scientist: Interactive Computer Elicitation of Personal Models Of The World. London, Academic Press.
Tomiyama, T. (1992). The technical concept of IMS. RACE Discussion Paper, No. RA-DP2, Research into Artifacts, Center for Engineering, The University of Tokyo.