 -calculus form for this item is:
-calculus form for this item is:
Key Centre for Advanced Computing Sciences
University of Technology, Sydney
PO Box 123, NSW 2007, Australia
The cost of managing system integrity increases with the degree of "volatility" of a system (Devedzic 1996). Volatile systems are systems which are subject to a high rate of change. Constraints are used to manage the integrity of the knowledge-based systems in which the knowledge base is volatile (Coenen & Bench-Capon 1992). This approach employs constraints for two distinct purposes:
Constraints are an integral part of the "conceptual model". The conceptual model is a complete representation of the knowledge required by the system; it specifies how the system will do what it is required to do (Debenham 1996d). The conceptual model consists of two parts. The first part is a representation of all things in the application as "items" (Debenham 1996b). The second part is a "coupling map" which supports the maintenance procedure (Debenham 1995). Items contain pragmatic constraints. Referential constraints simplify the structure of the coupling map. A tool which incorporates this approach has been built and trialed in a commercial environment.
The terms `data', `information' and `knowledge' are used here in a rather idiosyncratic sense. The data in an application are those things which are taken as the fundamental, indivisible things in that application; data things can be represented as simple constants or variables. The information is those things which are "implicit" associations between data things. An implicit association is one that has no succinct, computable representation. Information things can be represented as tuples or relations. The knowledge is those things which are "explicit" associations between information things or data things. An explicit association is one that has a succinct, computable representation. Knowledge things can be represented either as programs in an imperative language or as rules in a declarative language.
The conceptual model is not a complete system specification. The conceptual model does not contain details of which information items should be stored as relations in the relational database. The conceptual model does not contain details of how the knowledge items should be used to derive the values of those information items which are not physically stored as relations. The internal model is derived from the conceptual model by including both details of which information items should be stored as relations in the relational database, and details of how the knowledge items should be used to derive the values of those information items which are not physically stored as relations (Debenham & Devedzic 1996a). Once the internal model has been derived, referential constraints may be applied to the items in the conceptual model. These referential constraints simplify the coupling map, and thus improve the efficiency of the maintenance procedure.
Items have a uniform format no matter whether they represent data, information or knowledge. The key to this uniform representation is the way in which the "meaning" of an item, called its semantics, is specified. The semantics of an item is a function which recognises the members of the "value set" of that item. The value set of an information item is the set of tuples which are associated with a relational implementation of that item. Knowledge items, including complex, recursive knowledge items, have value sets too (Debenham 1996b). For example, the item which represents the rule "the sale price of parts is the cost price marked up by a universal mark-up factor" could have a value set as shown in Figure 1. Items incorporate two distinct classes of pragmatic constraints.
[part/sale-price, part/cost-price, mark-up]
| part/sale-price | part/cost-price | mark-up | |||||||||||||||||||||||||||||||||||
|
|
|
Figure 1: Value set of the item [part/sale-price, part/cost-price, mark-up]
Items are expressed in terms of their "components". For example, the knowledge item which represents the rule for marking-up the price of car spare parts will be expressed in terms of car spare parts. Also the knowledge item which represents the rule for marking-up the price of bike spare parts will be expressed in terms of bike spare parts. Items are thus unable to express the essence of the "mark up" rule. Objects are item building operators. Objects are not expressed in terms of particular components. Items and objects have a similar structure. The semantics of an object is a function which recognises the members of the "value set" of any item instance of that object operator. Objects incorporate two distinct classes of pragmatic constraints.
Pragmatic constraints apply equally to knowledge, information and data. A taxonomy of pragmatic constraints is:
A major collaborative research project between the University of Technology, Sydney and the CSIRO Division of Information Technology has addressed the effective maintenance of knowledge-based systems. The early results of this project are summarised in (Debenham 1989). Recent work in this project has focused on two issues. The first issue is the development of a unified framework for conceptual modelling in which the "data", "information" and "knowledge" in the application can all be represented entirely as "items" in a single formalism (Debenham & Devedzic 1996b). The second issue is the development of classes of constraints for knowledge which can protect the knowledge base effectively against the introduction of update anomalies. Early results on the development of knowledge constraints were reported in (Debenham 1989); more recent results are reported here. A key product of this collaborative research project has been the development of a complete methodology for the management of knowledge-based systems. This methodology is supported by a Computer Assisted Knowledge Engineering tool, or CAKE tool, called "The Knowledge Analyst's Assistant". An experimental version of this tool has been constructed (Debenham 1989) and has been trialed in a commercial environment.
 -calculus
expressions. Formally an item is a named triple
A[ SA, VA,
CA] where A is the item name, SA is
called the semantics of A, VA is called the
value constraints of A and CA is called the
set constraints of A. The i-schema notation for
representing items informally is shown in Figure 2. The
-calculus
expressions. Formally an item is a named triple
A[ SA, VA,
CA] where A is the item name, SA is
called the semantics of A, VA is called the
value constraints of A and CA is called the
set constraints of A. The i-schema notation for
representing items informally is shown in Figure 2. The  -calculus is
used to establish the formal properties of items. The i-schema are used to
specify items in practice.
-calculus is
used to establish the formal properties of items. The i-schema are used to
specify items in practice.
For example, an application could contain an association whereby each
part is associated with a cost-price. This association could be
subject to the value constraint that parts whose part-number is less that 1,999
will be associated with a cost price of no more than $300. This association
could be subject to the universal set constraint that every part must be in
this association, and the candidate set constraint that each part is associated
with a unique cost-price. This association could be represented by the
information item named part/cost-price. The i-schema for this
information item is shown in Figure 2. The  -calculus form for this item is:
-calculus form for this item is:
 xy · [Spart(x)
xy · [Spart(x)  Scost-price(y)
Scost-price(y)  costs(x, y)] ·,
costs(x, y)] ·,
 xy · [ Vpart(x)
xy · [ Vpart(x)  Vcost-price(y)
Vcost-price(y)  ((x < 1999)
((x < 1999) 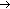 (y
(y  300)) ] ·,
300)) ] ·, Ccost-price
Ccost-price  (Uni(part)
(Uni(part)  Can(cost-price, {part}))part/cost-price ]
Can(cost-price, {part}))part/cost-price ]
|
||||||||||||||||||
| ||||||||||||||||||
Figure 2: i-schema format and the item 'part/cost-price'
Rules, or knowledge, can also be defined as items and thus can be represented using i-schema. Consider the rule "the sale price of parts is the cost price marked up by a universal mark-up factor"; suppose that this rule is represented by the item named [part/sale-price, part/cost-price, mark-up]. The idea of defining the semantics of items as recognising functions for the members of their value set extends to complex, recursive knowledge items too (Debenham 1996b). For example, the semantics of the [part/sale-price, part/cost-price, mark-up] item is:
 x1x2y1y2z·[Spart/sale-price(x1, x2)
x1x2y1y2z·[Spart/sale-price(x1, x2)
 Spart/cost-price(y1, y2)
Spart/cost-price(y1, y2)  Smark-up(z)
Smark-up(z) ((x1 = y1)
((x1 = y1) 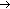 (x2 = z × y2))]·
(x2 = z × y2))]·
 Uni(part/cost-price)
Uni(part/cost-price)
 Can(part/sale-price, {part/cost-price, mark-up})
Can(part/sale-price, {part/cost-price, mark-up}) Can(part/cost-price, {part/sale-price, mark-up})
Can(part/cost-price, {part/sale-price, mark-up}) Can(mark-up, {part/sale-price, part/cost-price})
Can(mark-up, {part/sale-price, part/cost-price})
| [part/sale-price, part/cost-price, mark-up] | ||
| part/sale-price | part/cost-price | part/mark-up |
| (x, w) | (x, y) | z |
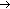 (w = z × y) (w = z × y) |
||
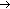 w > y w > y |
||
 |
 |
 |
| o | ||
| o | ||
| o | ||
Figure 3: [part/sale-price, part/cost-price, mark-up]
Constraints which constrain the way that an item is are called static constraints. The examples given above are all static constraints. In contrast, dynamic item constraints are constraints on how an item may be modified. An example of a dynamic item constraint on the knowledge item above is the requirement that if it is modified for any reason then the values in its value set associated with the component "part/sale-price" can only change by less than 10% of the previous values.
A single rule of "normalisation" may be specified for items (Debenham 1995). This rule may be applied to complex items, including complex knowledge items, to break them down into simpler items. From this single rule the five normal forms for relational database (Date 1986) may be derived as well as a comprehensive set of new normal forms for knowledge (Debenham 1996c).
Each object is an operator which turns n items into another item for some value of n. Further, the definition of each object will presume that the set of items to which that object may be applied are of a specific "type". The type of an m-adic item is determined both by whether it is a data item, an information item or a knowledge item and by the value of m. The argument type of an n-adic object is an n-tuple which specifies the types of the n items to which that object may be applied. Each of the n elements in an argument type will be "free" or "fixed". A free argument type is denoted by Xn and indicates that the object may be applied to any type of n-adic item and thus simply specifies the arity of that item. For example, if an object has argument type (X2, X2, X1) then it may be applied to any 2-adic item, followed by any other 2-adic item which is followed by any 1-adic item. A fixed argument type is denoted by Dn (standing for "data"), In (standing for "information") or Kn (standing for "knowledge") and indicates that the object can only be applied to an n-adic item of the nominated type. A fixed argument type specifies both the arity of each argument and whether that argument should be a data item, an information item or a knowledge item.
The formal definition of an object is similar to that of an item. An object is a named, typed triple A[E,F,G], where:
As for items, objects may be presented informally as "o-schema" or formally as
 -calculus expressions. The o-schema notation for representing
objects informally is shown in Figure 4.
-calculus expressions. The o-schema notation for representing
objects informally is shown in Figure 4.
The costs object of argument type (D1, D1) may be used to build the part/cost-price item:
costs(part, cost-price) = part/cost-price
The o-schema for the costs object is shown in Figure 4.
The mark-up-rule object of argument type (I2, I2, D1) may be used to build the [part/sale-price, part/cost-price, mark-up] item:
(part/sale-price,
|
|||||||||||||||||||||||||||
| |||||||||||||||||||||||||||
| Figure 4: o-schema format and the object 'costs' | |||||||||||||||||||||||||||
Figure 5: o-schema for object 'mark-up-rule'
|
|||||||||||||||||||||||||||
The conceptual model consists of both a representation of the things in the applications as "items", and a coupling map. The coupling map is a representation of the coupling relationships. These coupling relationships are of four distinct kinds (Debenham 1996a). First, duplicate relationships link two items which share some common meaning. In other words, a duplicate relationship indicates that a real fact has been represented, at least in part, in more than one place. Second, component relationships link each item to its components. For example, the component relationships for the item [part/sale-price, part/cost-price, mark-up] above are shown in Figure 6. Third, equivalence relationships link two items whose semantics are logically equivalent. Fourth, sub-item relationships link two items one of whose semantics logically implies the other's semantics.
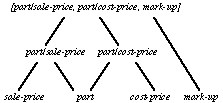
Figure 6: Component relationships
The coupling map can be simplified. The coupling map contains four kinds of coupling relationship. Duplicate relationships may be removed by applying the process of knowledge normalisation (Debenham 1996c). Some component relationships may be removed by applying referential constraints. Equivalence relationships may be removed by renaming. Sub-item relationships may be reduced to sub-type relationships.
Sub-item relationships join two items if one item is a sub-item of the other item. If a given data item is a sub-item of another data item then it is usual to say that the given data item is a sub-type of the other data item. For example, the item part1 could have as its value set all valid spare part numbers which lie between 1 and 1999, and the item part could have as its value set all valid spare part numbers; in this example part1 is a sub-type of part.
Sub-item relationships may exist between information items or knowledge items, but all sub-item relationships can be reduced to sub-type relationships between data items. For example consider the item car-part/cost-price shown in Figure 7. The structure at the top shows that this item is a sub-item of the item part/cost-price. The structure at the bottom shows how this sub-item relationship has been reduced to a sub-type relationship.
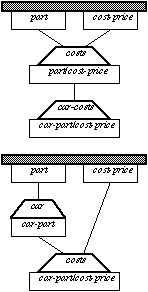
Figure 7: Reduction of sub-item relationship
In (Debenham 1996c) an "item join" operation is defined. Item join provides
the basis for item decomposition. Given items A and B, the item
with name A  E B is called the
join of A and B on E, where E is a set of components
common to both A and B. When two items are joined on the
component set which consists of all of their identical components we
omit the subscript of the join operator. Using the rule of composition
E B is called the
join of A and B on E, where E is a set of components
common to both A and B. When two items are joined on the
component set which consists of all of their identical components we
omit the subscript of the join operator. Using the rule of composition
 , knowledge items, information items and data items may be
joined with one another regardless of type. For example, the knowledge item:
, knowledge items, information items and data items may be
joined with one another regardless of type. For example, the knowledge item:
 xy·[x = y × 0.05]·,
xy·[x = y × 0.05]·,
 xy·[x < y]·, C[cost-price, tax] ]
xy·[x < y]·, C[cost-price, tax] ]
 {cost-price}part/cost-price =
{cost-price}part/cost-price =
 xyz·[costs(x,y)
xyz·[costs(x,y)  z = y ×
0.05]·,
z = y ×
0.05]·,
 xyz·[((1000<x<1999)
xyz·[((1000<x<1999)  (0<y
(0<y 300))
300))  (z<y)]·,
(z<y)]·,
 operator may form the basis of a theory of
decomposition in which each item may be replaced by a set of simpler items. An
item I is decomposable into the set of items D =
{I1, I2,..., In} if:
operator may form the basis of a theory of
decomposition in which each item may be replaced by a set of simpler items. An
item I is decomposable into the set of items D =
{I1, I2,..., In} if:
 I2
I2  ...
...  In , where
In , where
A conceptual model is said to be normal if the items and objects in it are not decomposable. Suppose that item I has the three components A, B and C. Consider the different ways in which this item I = I(C, B, A) can be decomposed into sub-items I1, I2 and I3. These different ways are categorised by the different ways in which functional associations are present in I; functional associations are represented by the candidate constraint. The different ways in which functional associations are present in a three component item lead precisely to the classical normal forms:
| 3NF | I((C, B) & A) = I2(C & B)  {B} I1(B & A) {B} I1(B & A) |
| 2NF | I(C & (B, A)) = I2(C & B)  {B} I1(B, A) {B} I1(B, A) |
| BC | I(B & (C, A)) = I2(C & B)  {B} I1(B, A) {B} I1(B, A) |
| 4NF | I(C, B, A) = I2(C,B)  {B} I1(B,A) {B} I1(B,A) |
| 5NF | I(C, B, A) = I3(A, C)  {C} I2(C, B) {C} I2(C, B)  {B} I1(B, A) {B} I1(B, A) |
The classical normal forms noted above apply equally well to knowledge as to data or information (Debenham 1996b). Thus the classical normal forms provide a complete characterisation of the different ways in which an item of three components may be decomposed. Further normal forms may be derived by considering decompositions of items of more than three components.
The maintenance procedure is guided by the coupling map. This procedure is
activated by the modification of an item. An item's semantics recognises the
members of its value set. Thus if an item's value set is modified then that
item's semantics has been modified. For example, the value set of the
part/cost-price item may be stored as a relation R. The predicate
"costs(x,y)" occurs in the semantics of this item. In strict terms, the
meaning of this predicate is "x costs y at time  ". If a tuple is added,
modified or deleted in the relation R then all of the coupling relationships
from the item part/cost-price must, in theory, be investigated. In
other words, each simple maintenance task on a relation can generate a
significant maintenance task. Referential constraints may be applied to
isolate the effect of simple maintenance tasks.
". If a tuple is added,
modified or deleted in the relation R then all of the coupling relationships
from the item part/cost-price must, in theory, be investigated. In
other words, each simple maintenance task on a relation can generate a
significant maintenance task. Referential constraints may be applied to
isolate the effect of simple maintenance tasks.
For example, consider a simple example in which [part/sale-price, part/cost-price, mark-up] is the only knowledge item in the conceptual model. Suppose that the internal model states that the mark-up data item and the part/cost-price information item should both be physically stored. That is, of the three distinct if-then interpretations of this single knowledge item, only the interpretation which derives the value set of the part/sale-price information item is required. The constraint that "the value set of the information item part/cost-price is fixed in the knowledge item [part/sale-price, part/cost-price, mark-up]" is an example of a referential constraint. This constraint means that if the tuples in the relation part/cost-price are modified then it is not necessary to follow the component link to the item [part/sale-price, part/cost-price, mark-up]. In other words "the validity of the knowledge item [part/sale-price, part/cost-price, mark-up] is invariant of the contents of the value set of its component information item part/cost-price". This referential constraint is a static constraint on the item [part/sale-price, part/cost-price, mark-up]; it states that this knowledge item must apply to any tuple which satisfies the item constraints of the information item part/cost-price. This constraint prunes the component relationship from the information item part/cost-price to the knowledge item [part/sale-price, part/cost-price, mark-up] in the instance when the value set of item part/cost-price is modified.
The referential constraint just considered has the effect of pruning a component relationship from an information item to a knowledge item. Component relationships from knowledge items to their constituent data or information items can be pruned in a similar way. For example, the constraint that "the value set of the knowledge item [part/sale-price, part/cost-price, mark-up]" is fixed on the information item part/cost-price " is an example of a referential constraint. This constraint means that if the item [part/sale-price, part/cost-price, mark-up] is modified then it is not necessary to follow the component link to the tuples of the relation part/cost-price. In other words "the validity of the value set of the information item part/cost-price is invariant of the item [part/sale-price, part/cost-price, mark-up]". This referential constraint is a static constraint on the information item part//cost-price. This constraint prunes the component relationship from the knowledge item [part/sale-price, part/cost-price, mark-up] to the information item part/cost-price in the instance when the clauses which implement the item [part/sale-price, part/cost-price, mark-up] are modified.
Date, C.J. 1986. An Introduction to Database Systems. (4th edition) Addison-Wesley, 1986.
Debenham, J.K. 1989. Knowledge Systems Design. Prentice Hall, 1989.
Debenham, J.K. 1995. Understanding Expert Systems Maintenance. In proceedings Sixth International Conference on Database and Expert Systems Applications DEXA'95, London, September 1995.
Debenham, J.K. 1996a. Characterising Maintenance Links. In proceedings Third World Congress on Expert Systems, Seoul, February 1996.
Debenham, J.K. 1996b. Integrating Knowledge Base and Database. In proceedings 10th ACM Annual Symposium on Applied Computing SAC'96, Philadelphia, February 1996, pp28-32.
Debenham, J.K. 1996c. Knowledge Simplification. In proceedings 9th International Symposium on Methodologies for Intelligent Systems ISMIS'96, Zakopane, Poland, June 1996.
Debenham, J.K. 1996d. Unification of Knowledge Acquisition and Knowledge Representation. In proceedings International Conference on Information Processing and Management of Uncertainty in Knowledge Based Systems IPMU'96, Granada, Spain, July 1996.
Debenham, J.K.; and Devedzic, V. 1996a. Designing Knowledge-Based Systems for Optimal Performance. In proceedings Seventh International Conference on Database and Expert Systems Applications DEXA'96, Zurich, Switzerland, September 1996, pp728-737.
Debenham, J.K.; and Devedzic, V. 1996b. Knowledge Analysis in KBS Design. In proceedings Seventh International Conference on Artificial Intelligence: Methodologies, Systems, Applications AIMSA'96, Sozopol, Bulgaria, September 1996, pp178-190.
Devedzic V. 1996. Organization and Management of Knowledge Bases: An Object-Oriented Approach. In proceedings of The Third World Congress on Expert Systems, Vol.II, Seoul, Korea, 1996, pp. 1263-1270.
Gray, P.M.D. 1989. Expert Systems and Object-Oriented Databases: Evolving a New Software Architecture. In Research and Development in Expert Systems V, Cambridge University Press, 1989, pp 284-295.
Kang, B.; Gambetta, W.; and Compton, P. 1996. Validation and Verification with Ripple Down Rules. International Journal of Human Computer Studies Vol 44 (2) pp257-270 (1996).
Lehner, F.; Hofman, H.F.; Setzer, R.; and Maier, R. 1993. Maintenance of Knowledge Bases. In proceedings Fourth International Conference DEXA93, Prague, September 1993, pp436-447.
Tayar, N. 1993. A Model for Developing Large Shared Knowledge Bases. In proceedings Second International Conference on Information and Knowledge Management, Washington, November 1993, pp717-719.