
Concept maps are used in a wide variety of disciplines because of their ability to make complex information structures explicit. Concept maps can be used informally or formally - where the graphical "syntax" of the maps is tightly controlled. Both forms are needed. Constraint Graphs is a program in which users can constrain arbitrary graphs to conform to any of a wide variety of graphical formalisms. The Constraint Graphs program is combined with a graphical user interface to yield an interactive concept mapping system, that can transcend informal concept mapping and at least several concept mapping formalisms.
Concept mapping is a simple and intuitive method of representing knowledge in a more flexible and natural form than is possible with other forms of representation such as pure text or strict formalisms (e.g. predicate logic). Concept maps are composed of nodes and arcs connecting the nodes. Nodes represent concepts and are labeled with a short description of the concepts. Arcs represent the relationships among the concept nodes and are usually labeled with a the relationship type. This simple notion leads to very powerful knowledge representation for both human understanding and computer processing.
For example, Figure 1 shows a concept map the may be developed by the participants in a decision-making meeting. The visual language used in Figure 1 is a semi-formalism called gIBIS (Graphical Issue Based Information System). Here, the elliptical nodes represent issues, the rounded-rectangular nodes represent positions taken on the issues, and the rectangular nodes represent arguments. The arcs connecting the nodes are all labeled with relationship types.
The decision making process represented in Figure 1 shows a clear and clean structure that would be quite difficult to represent using plain text. The relative linearity of text would obscure the relationships among the individual arguments and the sub-set of positions they related to. To be sure, a two-dimensional table could clearly represent the structure of most of Figure 1 (with the exception of the "standardization" part), but tables quickly become difficult as the complexity of the situation increases. The flexible, two-dimensional structure of the concept map is much more capable of clearly representing complex knowledge structures.

Concept maps can not only be used for decision making, but also for design, description, planning, brainstorming, scenario construction, and modeling. Furthermore, if concept maps are used in these ways, they can also serve as easy-to-collect corporate records of these activities. In addition, concept maps can be used in conjunction with hypermedia navigation systems to create "meta-concept maps" - concept maps that can be used to organize and navigate large collections of other concept maps.
If the "syntax" of concept maps is restricted (formalized) such that a semantics may be associated with them, then computer programs can be created to process the maps in various ways: for information retrieval, for decision support, and for knowledge-based inference by automated agents.
Thus, various forms of concept mapping are useful in industry for representing knowledge for both human understanding and computer support. But the different sorts of concept maps used in different ways may become difficult to handle and support. A central concept mapping system that could serve as a "shell" for all the different uses of concept maps would address this problem. The remainder of this paper describes just such as system.
Concept maps are graphs consisting of nodes with connecting arcs, which represent relationships between nodes (Lambiotte et al. 1984). The nodes are labeled with descriptive text, representing the "concept", and the arcs are often labeled with a relationship type. Nodes may be represented using distinct visual attributes, such as shape and color, to distinguish node types; arcs may be similarly distinguished.
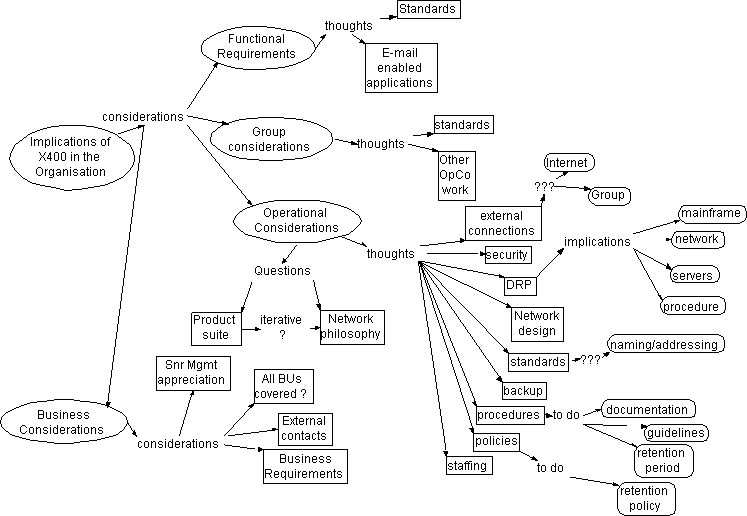
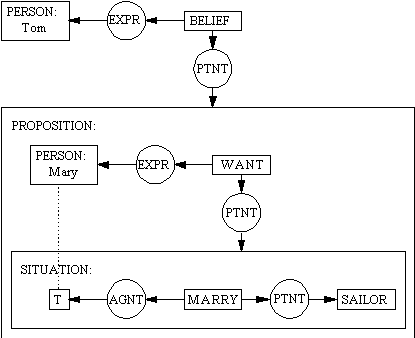
Figure 2 is an example of an informal concept map developed by a group during an interactive brainstorming session about a new network in a large company. In contrast, Figure 3 shows a formal concept map, called a Conceptual Graph (Sowa 1984), which models the sentence "Tom believes Mary wants to marry a sailor" in a way that is amenable to straightforward, unambiguous interpretation by a computer program.
Concept mapping (and the constraint graphs architecture in particular) is applicable to many areas of knowledge management in business. Business applications range from structured brainstorming (Figure 2) to "corporate memory" applications, to formal knowledge representation and execution such as expert systems.
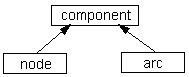
The purpose of a constraint graph is to provide an abstract mechanism to describe a graphical formalism. Constraint graphs are formally specified using a dialect of the specification language Z (Hayes 1987) called ZSL (Jia 1995). The complete specification is posted on the Web (Kremer 1996c). The basic premise is that all graphs contain only two basic object types: nodes and arcs (collectively referred to as components). Each of the basic types may be further elaborated into a lattice of subtypes. Each new subtype can introduce new attributes on top of those of its parent type. Constraint predicates can be attached to each subtype and are used as necessary to constrain the graph to conform to a particular formalism.
Interestingly, the traditional distinction between a type and an object is abandoned. But one may consider a component to be an object if it possesses a "~Exists x.x<this" predicate ("there is nothing that is a proper subtype of me"). Actually, the predicate "Forall x|x<this.~Exists y.y<x" ("nothing that is a proper subtype of me has any proper subtypes") is more common. For example, for the CLASSIC (Borgida et al. 1989) formalism, such a predicate is used to describe the fact the no Individual can be a superclass. (But the Individual object itself has to have subclasses, or there would be no individuals!)
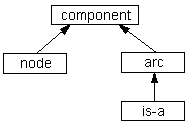
The type lattice of a constraint graph is fully integrated with the graph itself. That is, is-a arcs are just a subtype of the basic arc and are "drawn" into the graph just as any ordinary arc type (like owns, has-color, or bigger-than) would be. Of course, is-a adds several constraints on top of a basic arc because the is-a projection of the graph must be a lattice. These constrains include the fact that is-a arcs cannot form cycles and is-a arcs are always directed binary arcs. The type system is so well integrated with the graph system that users may specify the type of an object by drawing an is-a arc from the object to its type object (or by selecting its type from a menu at create time). Since the constraint graphs specification defines arc endpoints as terminating on components (not just nodes), a "separate" lattice of arcs (including is-a arcs) can also be formed, as required by the target formalism.
The addition, deletion, or modification of any component of a graph causes the system do a type check. This involves evaluating the constraint predicates and also related components. A constraint predicate takes as parameters the graph itself, the target object (the one in question), and the object that the predicate is actually attached to. Any component is legal if and only if
In addition, an arc (either isa or non-isa) is legal if and only if
Furthermore, an is-a arc is legal if and only if
A common concern is constraining the types of the objects in which
arcs can terminate. This is accomplished by simply attaching
the terminals of the defining arc to the appropriate type objects.
More complex cases can be handled using predicates. For example,
the brother relationship can be constrained (without bothering
with a male-person concept) by the constraint predicate
("brother is a binary relation between two persons where the second one is male"). Note that the second and third conjunct are redundant if
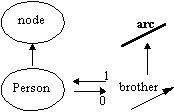
is drawn as the definition (by the second arc rule). Also note that the first conjunct, "this.arity=2" is still required to prevent a subtype of brother from becoming a trinary arc.
For convenience, a constraint graph is divided into levels. Level 1 consists of the graph types themselves - node, arc, is-a and composite - and is immutable as far as the user is concerned. The designation of the rest of the levels is left to the discretion of the formalism implementor. Generally, levels 2 and 3 should be at the system level where the basic types are defined according to the target formalism. These types should normally be considered immutable by any end users, since to disrupt them may compromise the interpretation of the graph. Two system levels are often used (where level 2 is hidden from the end user and used for hidden type hierarchies, while level 3 is public and used to populate the space of type identifiers for the end user). Level 4 is generally considered to be the user level, where the end user builds some specific knowledge structure. More levels are possible: for example, level 4 might be used to construct types in some specific domain, and a fifth level might be added to hold objects of that domain within some hypothetical world.
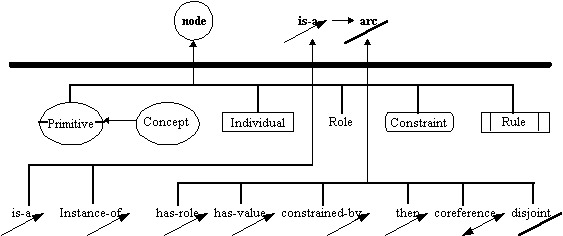
As an example, Figure 4 shows how a constraint graph can model KDraw (Gaines 1991), a visual form of CLASSIC (Borgida et al. 1989). The Constraint Graphs KDraw implementation is formally specified in Z in (Kremer 1996a). All the subtypes pictured below the heavy line in Figure 4 are not primitive in the constraint graph, but are added by a user describing KDraw. These all belong to level 3. The basic node types are concept, primitive, individual, constraint, and rule. KDraw has nine relations, two of which are subtypes of the is-a arc. The considerable semantics (rules) associated with the is-a arc (is-a arcs cannot form cycles, is-a arcs are binary, etc.) are automatically inherited by the subtype is-a and instance-of arcs.
Above the heavy line in Figure 4 are the primitive (level 1) objects of the constraint graph: node, arc, and is-a. Is-a is a subtype of arc (and forms the type lattice of a constraint graph).
Figure 5 shows an actual Constraint Graphs schema for the object types in KDraw. Node labels all begin with upper-case letters; arcs (relationships) are pictured as all lower-case letters. The surrounds of nodes are the same shape and style used in KDraw. Arcs in KDraw are all unlabeled (they are only labeled here for clarity), and for most part, are binary directed arcs (arrows) unambiguously distinguished by the (visual) type of their terminal objects. The cases where arcs types are not unambiguous are those in which the arc types have both terminals at concepts: Is-a, exclusive, and coreferent. These are visually disambiguated by Is-a being a directed arc, exclusive being an undirected arc, and coreferent being a double-directed arc.
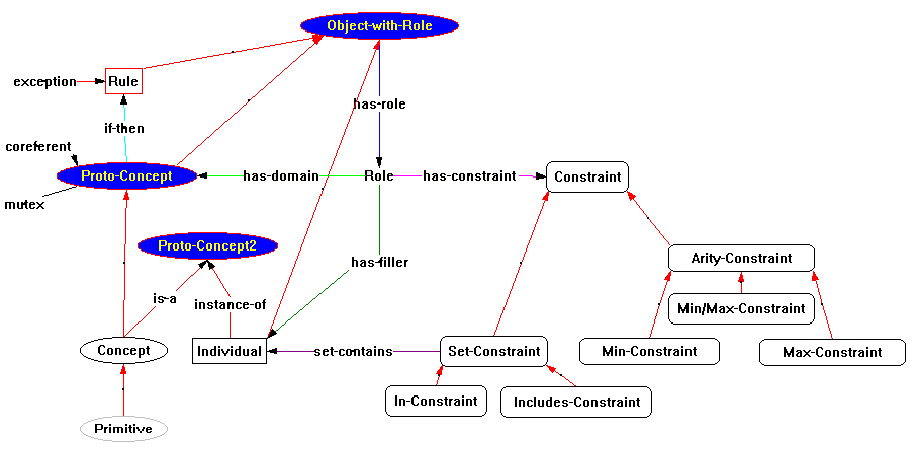
Of course, each of the objects shown in Figure 4 must be constrained to conform to the graphical syntax of KDraw. This is done in the Constraint Graph schema of Figure 5. For nodes, this is trivial, for the arcs alone suffice to control the syntax. (Any nodes could stand alone and unattached without violating any KDraw rules, but they wouldn't be very meaningful.) The only predicates applied to nodes are regular expression constraints which apply to the labels the end user puts on the various Constraint nodes. For the most part, arcs can be constrained by merely connecting their terminals to the appropriate type object (as per the second link rule above). These terminals are (almost) precisely those shown in Figure 5. Complications arise due to the need to introduce additional types to encapsulate "polymorphic" relationships (such as has-role), and to handle the natural inheritance of visual attributes from Concepts to Individuals through instance-of arcs without giving Individuals all the semantics of Concepts (to be detailed below).
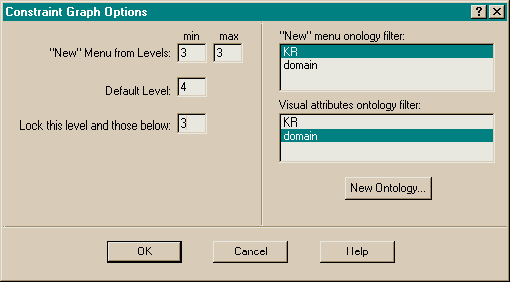
Figure 5 contains several nodes which are hidden from the user: Object-withRole, ProtoConcept, Constraint, Set-Constraint, and Arity-Constraint. These are hidden by placing them in level 2, and blocking level 2 from end user visibility using the options dialog (Figure 6). The purpose of these nodes is to allow "polymorphic" relationships between nodes. For example, there are four node types that can be the root of a has-role arc - Concept, Primitive, Rule, and Individual. This similarity is captured by introducing the (hidden) common supertype Object-with-Role. Similarly, the commonality among the various Constraint types is captured by hidden common supertypes.
There are several other constraints necessary to emulate KDraw. These are added as predicates:
These links and rules are sufficient to constrain a graph to the legal graphical syntax of a KDraw. (It's still possible to construct a nonsensical graph, but that's another story!)
The distinctive shapes of the node surrounds in KDraw are modeled by attributes in the constraint graph system. The nodes in the KDraw domain are each given a shape attribute: for example, concept has "shape=ellipse", role has "shape=none". Attributes are inherited by subtypes; so, all subtypes of concept will have the "shape=ellipse" attribute. But things are not that simple, as the example in Figure 7 shows. In this example, one needs to say not only that George is an instance-of Person, but also that George is-a individual. Clearly George is (and should be) both a subtype of the concept Person and of Individual. The semantics of KDraw dictates that the surround for George should be a rectangle and not an ellipse. But George inherits both "shape=rectangle" (from individual) and "shape=ellipse" (from person). How are these properly disambiguated? One may consider disambiguating using the predicates, but this would only allow or disallow a particular configuration; what is needed is a way to automatically and efficiently choose the correct shape. The system used in Constraint Graphs is to extend attributes with properties. One of those properties is priority, which is of type natural number, {0, 1, 2, …}. The highest priority is 0. Using this scheme, individual's shape attribute is given the priority 0, and concept's shape attribute is given the priority 1. Thus, the system is able to unambiguously compute George's shape as rectangle.
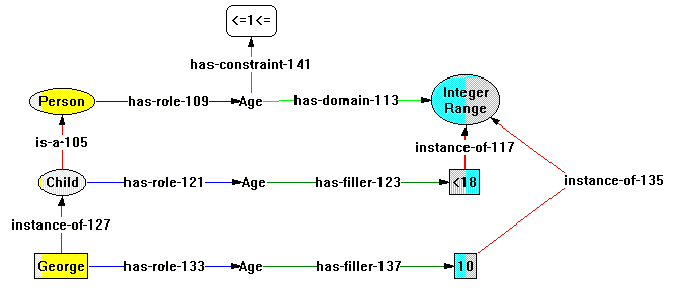
A related problem is that George should naturally inherit the color that the user has given to Person, since George is an instance-of Person. Instance-of is a subtype of isa, so the color inheritance happens naturally. But Individuals must not inherit other abilities that a Concept supertype might have, such as the ability to be on the root side of a has-rule relationship (see Figure 5). This trick is accomplished by filtering appropriate isa arcs. The arc instance-of-127 is tagged (by a predicate rule in instance-of) with the domain filter (used by the visual inheritance system), while the graph is using the (mutually exclusive) KR filter to determine arc eligibility (see Figure 6).
Another problem arises because the visual syntax of KDraw is completely dictated by the surround shape; that is, users expect ellipses to represent concepts, rectangles to represent individuals, etc. If a user were to override the shape of concept for instance, the concept map would be rendered unreadable (but still computable, because the system uses abstract types, not shape). On the other hand users could override other attributes, such as color, without effecting the readability of the map. This problem is solved by again using properties of attributes. A second property, constant, is introduced. A constant attribute cannot be overridden by any object at a lower level. Thus, the shape attribute can be locked on all KDraw objects, preventing users from changing the shape, while still allowing them to change attributes like color. Locking could easily be accomplished by using predicates, but since it occurs relatively often it is a part of the attribute system, where it is more convenient to specify.
The Constraint Graph program is capable of capturing the syntax of other graphical formalisms by inferencing via the type lattice, but the reader should note that it is not intended to take on the deeper semantic nuances of any arbitrary graphical formalism. For example, although it can emulate the syntax of KDraw, Constraint Graph cannot do the inferences of KDraw.
However, the Constraint Graph program is relatively easy to extend to "compile" a graph into the native notation of a target formalism. For example, it took only a single day to write an extension to output the graph as a complete Z specification - this automatic generation produced the specifications found in (Kremer 1996a) and (Kremer 1996b). Future work on this project includes adding an extension to compile a graph into KDraw's native notation, calling up a separate KDraw interpreter (possibly elsewhere on the Internet), and writing back the inferences into the original graph.
The constraint graphs program itself lacks a graphical interface. The figures produced here are done by combining the constraint graphs program with an program called KSIMapper. KSIMapper is a graphical concept mapping program. Each time a user creates a new component in the KSIMapper interface, a corresponding component is created in the constraint graph. The component in the constraint graph is checked for legality. If it is not legal, the creation is undone in both places and an appropriate message dispatched to the user. Likewise, for any modification to an object in the interface (such as changing the value of an attribute) the corresponding change is made in the constraint graph, checked for legality, and undone if it is not legal. Thus, the graphical interface is always kept in conformance to legal syntax according to the constraint graph.
Changes in one place in the graph may affect changes in other places in the graph. For example, if the person concept has the attribute "color=green", and a user changed the attribute to "color=blue", then (assuming no subtype overrides the attribute value) all subtypes of person (primitive-concepts, concepts, or individuals) should also change their color to blue. This is accomplished easily in the program because when an KSIMapper component/constraint graphs component pair is created the two are linked using the observer pattern (Gamma et al. 1995) so that any changes to the Graphs object are broadcast to the corresponding KSIMapper object. When any attribute of a Graphs object changes, the changes are automatically propagated to all subtypes which, in turn, broadcast the update to all their observers in KSIMapper.
Since the two parts of the program, KSIMapper and Graphs, have such a high degree of independence, it should be relatively easy to reconfigure the software. For example, one could start with a very informal map drawn with KSIMapper alone (which imposes no constraints), and then "clip-on" a KDraw constraint graph to allow the gradual "formalization" of the map to match KDraw syntax. Work in this area has not yet been undertaken, but it looks relatively straight-forward. A more difficult problem is the smooth transition from one formalism to another (related) one. There are many more problems here, having to do with phasing out of one formalism and the introduction of another without producing too much inconsistency in the meantime.
Efficiency is also a significant problem in the current version of the software. The independence of the two halves of the program is paid for by a certain amount of redundancy, both in terms of space and time complexity. The checking of the legality of a object in a constraint graph also has a polynomial time complexity on the number of objects in the graph according the specification. Actually, one of the implementations of the specification caches relationships, and so the time complexity is reduced to polynomial on the depth of the graph. However, there is lots of room for improvement here.
Constraint graphs have only been applied to KDraw, Conceptual Graphs, and gIBIS to date. Applying them to other graphical formalisms such as Petri nets would be useful to show the utility of constraint graphs. This may also serve to further generalize the tool.
Concept maps are an intuitive form of knowledge representation. Concept maps can be used in informal (unstructured) forms as well as formal (structured) forms. The constraint graphs program is designed to emulate many graphical formalisms. It can be used to constrain an internally represented graph to conform to many graphical formalisms via a user-specifiable type lattice augmented by object attributes and "constraint predicates".
The constraint graphs program can be combined with the KSIMapper graphical interface. In this way, a flexible, multi-user, programmable concept mapping "shell" is formed.
It is still early in the life cycle of these programs. Exactly how easy it is to configure constraint graphs to handle other formalisms (other than its it initial test cases) remains to be seen. Efficiency considerations need to be addressed as well. Furthermore, the KSIMapper user interface is still quite rarefied and needs to be extended to handle several common direct manipulation features. Finally, it will be interesting to study whether such a system can simplify the transition between informal and formal systems.
Concept mapping applies to knowledge management in industry in both informal and formal forms for human comprehension and computer support respectively. However, the diversity of uses implies a variety of concept mapping "languages". A high-level, configurable system such as Constraint Graphs may be an ideal way to deal with the variety.
Axelrod, R. 1976. Structure of Decision. Princeton, New Jersey, Princeton University Press.
Banathy, B. H. 1991. Cognitive mapping of educational systems for future generations. World Future 30(1): 5-17.
Borgida, A., Brachman, R. J., McGuiness, D. L. & Resnick, L. A. 1989. CLASSIC: A Structural Data Model for Objects. Proceeding of 1989 SIGMOD Conference on the Management of Data. New York, ACM Press: 58-67.
Eden, C., Jones, S. & Sims, D. 1979. Thinking in Organizations. London, Macmillan.
Eklund, P. W., Leane, J. & C., N. 1993. GRIT: Toward a Standard GUI for Conceptual Structures. Second International Workshop on PEIRCE: A Conceptual Graphs Workbench. Laval University, Quebec, Canada.
Ellis, G. & Levinson, R., Eds. 1992. Proceedings of the First International Workshop on PEIRCE: A Conceptual Graphs Workbench. Las Cruccs, New Mexico.
Gaines, B. R. 1991. An Interactive Visual Language for Term Subsumption Languages. IJCAI-91. Sydney, Australia.
Gamma, E., Helm, R., Johnson, R. & Vlissides, J. 1995. Design Patterns: Elements of Reusable Object-Oriented Software. Reading Mass., Addison Wesley.
Graesser, A. C. & Clark, L. F. 1985. Structures and Procedures of Implicit Knowledge. New Jersey, Ablex.
Hart, J. A. 1977. Cognitive maps of three latin american policy makers. World Politics 30(1): 115-140.
Hayes, I., Ed. 1987. Specification Case Studies. Englewood Cliffs, N. J., Prentice-Hall.
Jia, X. 1995. ZTC: A type checker for Z (version 2.02). ftp://ise.cs.depaul.edu/pub/ZTC/, September 29,1996.
Kremer, R. 1993. A Concept Map Based Approach to the Shared Workspace. MSc. Thesis, Department of Computer Science, University of Calgary, Calgary, Canada.
Kremer, R. 1994. Concept Mapping: Informal to Formal. Third International Conference on Conceptual Structures, Knowledge Represetnation Workshop. University of Maryland.
Kremer, R. 1995. The Design of a Concept Mapping Environment for Knowledge Acquisition and Knowledge Representation. Banff Knowledge Acquisition Workshop. Banff, Alberta.
Kremer, R. 1996a. A Z Specification for KRS using Typed Graphs. http://www.cpsc.ucalgary.ca/~kremer/graphs/KRS_Z.html, September 30, 1996.
Kremer, R. 1996b. A Z Specification for the Conceptual Graphs based on of Typed Graphs. http://www.cpsc.ucalgary.ca/~kremer/graphs/CG_Z.html, September 30, 1996.
Kremer, R. 1996c. A Z Specification for the Formal Interpretation of Typed Graphs. http://www.cpsc.ucalgary.ca/~kremer/graphs/graphsZ2.html, September 30, 1996.
Lambiotte, J. G., Dansereau, D. F., Cross, D. R. & Reynolds, S. B. 1984. Multirelational Semantic Maps. Educational Psychology Review 1(4): 331-367.
McNeese, M. D., Zaff, B. S., Peio, K. J., Snyder, D. E., Duncan, J. C. & McFarren, M. R. 1990. An Advanced Knowledge and Design Acquisition Methodology for the Pilot's Associate. Wright-Patterson Air Force Base, Ohio, Harry G. Armstrong Aerospace Medical Research Laboratory.
Nosek, J. T. & Roth, I. 1990. A Comparison of Formal Knowledge Representation Schemes as Communication Tools: Predicate Logic vs. Semantic Network. International Journal of Man-Machine Studies 33: 227-239.
Novak, J. D. & Gowin, D. B. 1984. Learning How To Learn. New York, Cambridge University Press.
Quillian, M. R. 1968. Semantic memory. Semantic Information Processing. M. Minsky. Cambridge, Massachusetts, MIT Press: 216-270.
Sowa, J. F. 1984. Conceptual Structures: Information Processing in Mind and Machine. Reading, Massachusetts, Addison-Wesley.