Dieter Fensel and Richard Benjamins
University of Amsterdam, Department SWI
Roetersstraat 15, 1018
WB Amsterdam, the Netherlands,
E-mail: {fensel | richard}@swi.psy.uva.nl
In [Fensel & Straatman, 1996] we discussed the idea of viewing the development process of an efficient knowledge-based reasoner as a process of introducing and refining assumptions. A simple generate & test problem solver is modified to a more efficient problem-solving method (a variant of propose & revise for parametric design by introducing assumptions that weaken the task and that strengthen the requirements on domain knowledge. In this paper, we review the work on diagnostic reasoning systems. We focus on assumptions that are introduced to define the effect of diagnostic reasoners and to improve their efficiency. The work on diagnostic reasoning provides an interesting empirical basis for our approach as it provides a more than ten years long history on developing knowledge-based reasoners for a complex task. During this process, several assumptions have been identified and refined in the literature on model-based diagnostic systems.
The first diagnostic systems built were heuristic systems, in the sense that they contained compiled knowledge which linked symptoms directly to hypotheses (usually in rules). In these systems, only foreseen symptoms can be diagnosed and heuristic knowledge that links symptoms with possible faults needs to be available. One of the main principles underlying model-based diagnosis is the use of a domain model (called SBF models in [Chandrasekaran, 1991]). Heuristic knowledge that links symptoms with causes is no longer necessarily. The domain model is used for predicting the desired device behaviour, which is then compared to the observed device behaviour. A discrepancy indicates a symptom. General reasoning techniques as constraint satisfaction or truth maintenance can be used to derive diagnoses that explain the actual behaviour of the device using its model. Because the reasoning part is represented separately from domain knowledge, it can be reused for different domains. This paradigm of model-based diagnosis gave rise to the development of general approaches to diagnosis, such as ``constraint suspension`` [Davis, 1984], DART [Genesereth, 1984], GDE [de Kleer & Williams, 1987], and several extensions to GDE (GDE+ [Struss & Dressler, 1989], Sherlock [de Kleer & Williams, 1989]).
In
this paper, we will focus on assumptions underlying approaches to diagnostic
problem solving. In Section 2, we discuss assumptions that are necessary to
relate a diagnostic system with its environment. That is, assumptions on the
available case data, the required domain knowledge and the problem type. In
Section 3, we discuss assumptions introduced to reduce the complexity of the
reasoning process necessary to execute the diagnostic task. Such assumptions are
introduced to either change the worst-case complexity or the average-case
behaviour of problem solving. In Section 4, we sketch further assumptions that
are related to the efficiency of the interaction of the problem solver with its
environment. Section 5 sketches a general framework for specifying reasoning
systems and their underlying assumptions. It discusses how assumptions can be
used to weaken or strengthen the problem-solving method competence. In section 6,
we present conclusions.
2 The Task: Assumptions
for Effect
In model-based diagnosis (cf. [de Kleer et al., 1992]), the definition of the task of the KBS
requires a system description of the device under consideration and a
set of observations, where some indicate normal and other
abnormal behaviour. The goal of the task is to find a diagnosis
that, together with the system description, explains the observations.
In the following, we discuss four different aspects of such a task definition and
show the assumptions related to each of them. The four aspects are: identifying
abnormalities, identifying causes of these abnormalities, defining hypotheses,
and defining diagnoses.
2.1 Identifying
Abnormalities
Identification of abnormal behaviour is
necessary before a diagnostic process can be started to find explanations for the
abnormalities. This identification task requires three kinds of knowledge, of
which two are related to the type of input, and one to the interpretation of
possible discrepancies (see [Benjamins, 1993]):
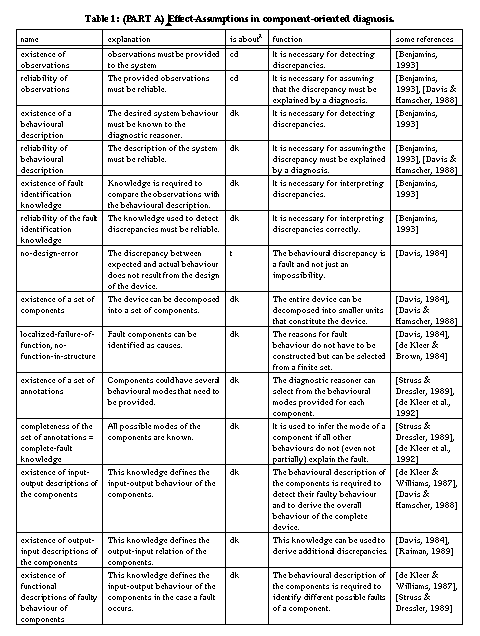
These assumptions are also necessary for the meta-level decision whether a diagnosis problem is given at all (i.e., whether there is an abnormality in system behaviour). This decision relies on a further assumption: the no-design-error assumption [Davis, 1984] which says that if no fault occurs, then the device must be able to achieve the desired behaviour. In other words, the discrepancy must be the result of a fault situation where some parts of the system are defect. It cannot be the result of a situation where the system works correctly, but cannot achieve the desired functionality because it is not designed for this. If this assumption does not hold, one has a design problem and not a diagnostic problem.
2.2 Identifying
Causes
Another purpose of the system description is the
identification of causes of faulty behaviour. This cause-identification knowledge
must be reliable [Davis & Hamscher, 1988], or,
in other words, the knowledge used in model-based diagnosis is assumed to be a
correct and complete description of the artefact. Correct and complete in the
sense, that it enables the derivation of correct and complete diagnoses if
discrepancies appear. In accordance with different types of device models and
diagnostic methods, these assumptions wear different clothes. During the
following we restrict our attention to component-oriented device models that
describe a device in terms of components, their behaviours (a functional
description), and their connections. The set of all possible hypotheses is the
power-set of the set of annotated components
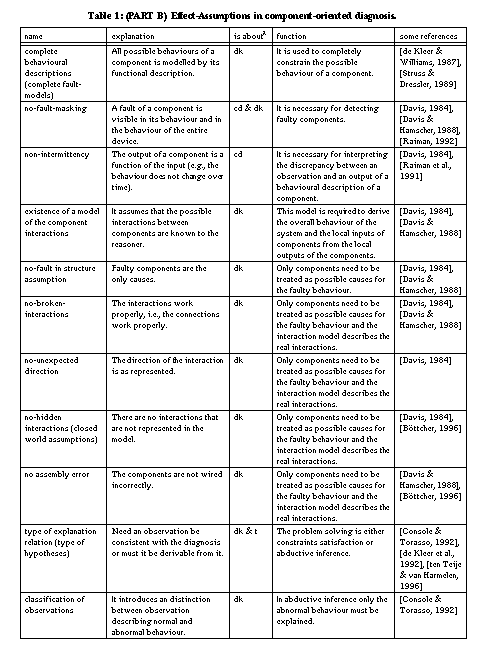
First, the localised-failure-of-function assumption: the device must be decomposable in well-defined and localised entities (i.e., a component) that can be treated as causes of faulty behaviour. Second, these components have a functional description that provides the (correct) output for their possible inputs. If this functional description is local, that is, it does not refer to the functioning of the whole device, the no-function-in-structure assumption [de Kleer & Brown, 1984] is satisfied. Several diagnostic methods can also use the reverse of the functional descriptions, thus, rules that derive the expected input from the provided output. If only correct functional descriptions are available, fault behaviour is defined as any other behaviour than the correct one. Fault behaviour of components can be constrained by including fault models, that is, functional descriptions of the components in case they are broken (cf. [de Kleer & Williams, 1989], [Struss & Dressler, 1989]). If one assumes that these functional descriptions are complete (the complete fault-knowledge assumption), then components can be considered innocent if none of their fault descriptions is consistent with the observed fault behaviour. A result of using fault models is that all kinds of non-specified behaviours of a component are excluded as diagnosis. For example, using fault models, it becomes impossible to conclude that a fault (one of two light bulbs is not working) is explained by a defect battery that does not provide power and a defect lamp that lights without electricity (cf. [Struss & Dressler, 1989]).
Further assumptions that are related to the functional descriptions of components are the no-fault-masking and the non-intermittency assumption. The former states that the defect of an individual or composite component, or of the entire device must be visible by changed outputs (cf. [Davis & Hamscher, 1988], [Raiman, 1992]). According to the latter, a component that gets identical inputs at different points of time, must produce identical outputs. In other words, the output is a function of the input (cf. [Raiman et al., 1991]). They argue that intermittency results from incomplete input specifications of components, but that it is impossible to get rid of it (it is impossible to represent the required additional inputs).
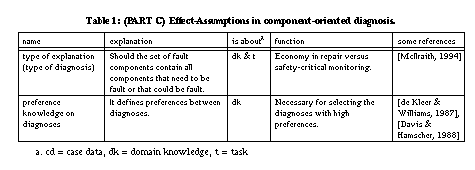
A third assumption underlying many diagnostic approaches is the no-faults-in-structure assumption (cf. [Davis & Hamscher, 1988]) that manifests itself in different variants according to the particular domain. The assumption states that the interactions of the components are correctly modelled and that they are complete. This assumption gives rise to three different classes of more specific assumptions. First, the no-broken-interaction assumption states that connections between the components work correctly (e.g. no wires between components are broken). If this is not the case, the assumption can be weakened by representing the connections themselves as components too. Second, the no-unexpected-directions assumption (or existence of a causal-pathway assumption) states that the directions of the interactions are correctly modelled and are complete. For example, a light-bulb gets power from a battery and there is no interaction in the opposite direction. The no-hidden-interactions assumption (cf. [Böttcher, 1996]) assumes that there are no non-represented interactions (i.e., closed-world assumptions on connections). A bridge fault [Davis, 1984] is an example of a violation of this assumption in the electronic domain. Electronic devices whose components unintendedly interact through heat exchange, is another example [Böttcher, 1996]. In the worst case, all potential unintended interaction paths between components are represented [Preist & Welhalm, 1990]. The no-hidden-interactions assumption is critical since most models (like design models of the device) describe correctly working devices and unexpected interactions are therefore precisely not mentioned. A refinement of this assumptions is that there are no assembly errors (i.e., every individual component works but they have been wired up incorrectly).
2.3 Defining Hypotheses
In addition to
knowledge that is required to identify a discrepancy and knowledge that provides
hypotheses used to explain these discrepancies, one requires further knowledge to
decide which type of explanation is required. [Console &
Torasso, 1992] distinguish two types of explanations: weak explanations, that
are consistent with the observations (no contradiction can be derived
from the union of the device model, the observations, and the hypothesis), and
strong explanations, that imply the observations (the observations can
be derived from the device model and the hypothesis). Both types of explanation
can be combined by dividing observations in two classes: observations that need
to be explained by deriving them from a hypothesis, and observations that need
only be consistent with the hypothesis. In this case one requires knowledge
that allows to divide the set of observations. The decision which type of
explanation to use, can only be made based on assumptions about the environment
in which the KBS is used.
2.4 Defining
Diagnoses
Having established observations, hypotheses
and an explanatory relation that relates hypotheses with observations, one must
establish the notion of diagnosis. Not each hypothesis that correctly
explains all observations needs to be a desired diagnosis. One could accept only
parsimonious hypotheses as diagnoses (cf. [Bylander et al., 1991]). An hypothesis or explanation H is
parsimonious if H is an explanation and there exists no other hypothesis
H' that also is an explanation and H' < H.
H is a diagnosis if H is a parsimonious explanation. One has to
make assumptions about the desired diagnosis (cf. [McIlraith,
1994]) in order to define the partial ordering (<) on hypotheses. For
example, whether the diagnostic task is concerned with finding all components
that are necessarily fault to explain the system behaviour, or whether it is
concerned with finding all components that are necessarily correct to explain the
system behaviour. In the first case, we aim at economy in repair, whereas in
safety critical applications (e.g., monitoring of nuclear power plants) one
should obviously choose for the second case.
As shown by [McIlraith, 1994], the assumptions about the type of explanation relation (i.e., consistency versus derivability) and about the explanations (i.e., definition of parsimony) make also strong commitments on the domain knowledge (the device model) that is used to describe the system. If we ask for a consistent explanation with minimal sets of fault components (i.e., H1 < H2 if H1 assumes less components as being fault than H2), we need knowledge that constrains the normal behaviour of components. If we ask for a consistent explanation with minimal sets of correct components (i.e., H1 < H2 if H1 assumes less components as being correct than H2), we need knowledge that constrains the abnormal behaviour of components.
The definition of parsimonious
hypotheses introduces a preference on hypotheses. This could be extended
by defining further preferences on diagnoses to select one optimal one (e.g., by
introducing assumptions related to the probability of faults). Again, knowledge
about preferences must be available to define a preference function and a
corresponding ordering.
2.5 Summary
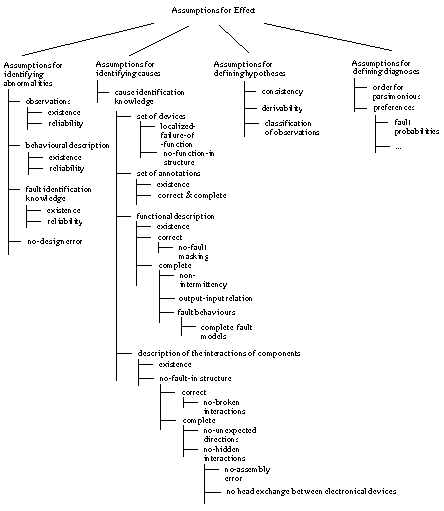
Figure 1 summarises the assumptions that are
discussed above and groups them according to their purpose. All these assumptions
are necessary to relate the definition of the functionality of the diagnostic
system with the diagnostic problem (i.e., the task) to be solved and with the
domain knowledge that is required to define the task. Table
1 provides an explanation of the assumptions along with the role they play
(function), the domain they are about (case data, domain knowledge or task), and
some references where they are discussed in more detail.
Figure 1 Assumptions for Effect
3 The Problem Solver: Assumptions for Efficiency
Besides the assumptions that are necessary to define the
task, further assumptions are necessary because of the complexity of model-based
diagnosis. Component-based diagnosis is in the worst case exponential in the
number of annotated components ([Bylander et al., 1991]).
Every element of the power-set of the set of annotated components is a possible
hypothesis. As we are not interested in problem-solving in principle but in
practice, further assumptions have to be introduced that either decrease the
worst-case, or at least the average-case behaviour.
3.1 Reducing the Worst-Case Complexity: The Single-Fault Assumption
A drastic way to reduce the complexity of the diagnostic
task is achieved by the single-fault or N-fault assumption
(SFA) [Davis, 1984], which reduces the complexity to
polynomial in the number of components. If the single-fault assumption holds, the
incorrect behaviour of the device is completely explainable by one failing
component. This assumption defines either strong requirements on the provided
domain knowledge, or significantly restricts the diagnostic problems that can
correctly be handled by the diagnostic system (cf. [Benjamins et
al., 1996]).
If the SFA has to be satisfied by the domain knowledge, then each possible fault has to be represented as a single entity. In principle this causes complexity problems for the domain knowledge as each fault combination (combination of fault components) has to be represented. However, additional domain knowledge can be used to restrict the exponential increase. [Davis, 1984] discusses an example of a representation change where a 4-fault case (i.e., 15 different combinations of faults) is transformed into a single fault. A chip with four ports can cause faults on each port. When we know that the individual ports never fail, but only the chip as a whole, a fault on four ports can be represented as one fault of the chip. Even without such a representation change, we do not necessarily have to represent all possible fault combinations. We can, for example, exclude all combinations that are not possible or likely in the specific domain (expert knowledge).
Instead of formulating the requirement above
on the domain knowledge, one can also weaken the task definition by this
assumption. This means that the competence of the PSM meets the task definition
under the assumption that only single fault occurs. That is, only in cases where
a single fault occurs, the method works correctly and complete. This would imply
that the diagnostic system is designed for simple routine diagnoses.
3.2 Reducing the Average-Case Behaviour: The Minimality
Assumption of GDE
As the SFA might be too strong an
assumption for several applications, either as a requirement on the domain
knowledge or as a restriction on the task, [Reiter, 1987] and
[de Kleer & Williams, 1987] provide approaches able to
deal with multiple faults. However, this re-introduces the complexity problems of
MBD. To deal with this problem, GDE [de Kleer & Williams,
1987] exploits the minimality assumption, which reduces, in
practical cases, the exponential worst case behaviour to a complexity that grows
with the square of the number of components. In GDE, this assumptions helps
reducing the complexity in two ways. First, a conflict is a set of components
where it cannot be the case that all components work correctly given the provided
domain knowledge and the observed behaviour. Under the minimality assumption,
each super-set of a conflict is also a conflict and all conflicts can be
represented by minimal conflicts. Second, a hypothesis contains at least one
component of each conflict. Every super-set of such a hypothesis is again a
hypothesis. Therefore, diagnoses can be represented by minimal diagnoses. The
minimality assumption requires that diagnoses are independent or monotonic (see
[Bylander et al., 1991]): a diagnosis that assumes more
components as being faulty, explains more observations.
A drastic way to ensure that the minimality assumption holds, is to neglect any knowledge about the behaviour of faulty components. Thus, any behaviour that is not correct is considered as fault. A disadvantage of this is that physical rules may be violated (i.e., existing knowledge about faulty behaviour). We already mentioned the example provided in [Struss & Dressler, 1989], where a fault (one of two bulbs does not light) is explained by a broken battery that does not provide power and a broken bulb that lights without power. Knowledge about how components behave when they are faulty (called fault models) could be used to constrain the set of diagnoses derived by the system. On the other hand, it increases the complexity of the task. If for one component m possible fault behaviours are provided, this leads to m+1 possible states instead of two (correct and fault). The maximum number of candidates increases from 2n to (m+1)n.
A similar extension of GDE that includes fault models, is the Sherlock system (cf. [de Kleer & Williams, 1989]). With fault models, it is no longer guaranteed that every super-set of the faulty components that constitute the diagnosis, is also a diagnosis, and therefore the minimality assumption as such cannot be exploited. In Sherlock, a diagnosis does not only contain fault components (and implicitly assumes that all other, not mentioned, components are correct), but it contains a set of components assumed to work correctly and a set of components assumed to be fault. A conflict is now a set of some correct and fault components that is inconsistent with the provided domain knowledge and the observations. In order to accommodate to this situation, [de Kleer et al., 1992] extend the concept of minimal diagnoses to kernel diagnoses and characterise the conditions under which the minimality assumption still holds. The kernel diagnoses are given by the prime implicants of the minimal conflicts. Moreover, the minimal sets of kernel diagnoses sufficient to cover every diagnosis correspond to the irredundant sets of prime implicants of all minimal conflicts. These extensions cause drastic additional effort, because there can be exponentially more kernel diagnoses than minimal diagnoses, and finding irredundant sets of prime implicants is NP-hard. Therefore, [de Kleer et al., 1992] characterise two assumptions under which the kernel diagnoses are identical to the minimal diagnoses. The kernel diagnoses are identical to the minimal diagnoses if all conflicts contain only fault components. In this case, there is again only one irredundant set of minimal diagnoses (the set containing all minimal diagnoses). The two assumptions that can ensure these properties are the ignorance-of-abnormal-behaviour assumption and the limited-knowledge-of-abnormal-behaviour assumption.
The ignorance-of-abnormal-behaviour assumption excludes knowledge
about faulty behaviour and thus characterises the original situation of GDE. The
limited-knowledge-of-abnormal-behaviour assumption states that the knowledge of
abnormal behaviour does not rule out any diagnosis indicating a set of fault
components, if there exist a valid diagnosis indicating a subset of them as
faulty components, and if the additional assumed fault components are not
inconsistent with the observations and the system description. The latter
assumption is a refinement of the former, that is, the truth of the
ignorance-of-abnormal-behaviour assumption implies the truth of the
limited-knowledge-of-abnormal-behaviour assumption.
3.3 Search Guidance
The complexity
of component-based diagnosis (especially when working with fault models) requires
further assumptions that enable efficient reasoning for practical cases (cf. [Struss, 1992], [Böttcher & Dressler,
1994]). Again, these assumptions do not change the worst case complexity but
should reduce the necessary effort in practical cases. A well-known notion to
increase efficiency is a reasoning focus. Defining a focus for the reasoning
process can be achieved by exploiting hierarchies or probability information. The
hierarchically-layered device-model assumption assumes the existence of
hierarchically layered models that allow step wise refinement of diagnosis to
reduce the complexity of the diagnostic process (cf. the complexity analysis of
hierarchical structures of [Goel et al., 1987]). The large
number of components at the lowest level of refinement is replaced by a small
number of components at a higher level. Only the relevant parts of the model are
refined during the problem-solving process. The hierarchically-layered
behavioural-model assumption assumes the existence of more abstract
descriptions of the behaviour that can improve the efficiency because reasoning
can be performed at a more coarse grained, and thus simpler, level (cf. [Abu-Hanna, 1994]). The existence-of-probabilities
assumption assumes knowledge about the probability of faults that can be used to
guide the search process for diagnoses by focusing on faults with high
probabilities. Usually, these probabilities introduce new assumptions (e.g., the
components-fail-independently assumption [de Kleer &
Williams, 1989]).
All these knowledge types and their
related assumptions rely on further assumptions concerning the utility of this
search control knowledge. For example, the hierarchically-layered device model
improves only the search process when the faults are not distributed in a way
that enforces the problem solver to expand each abstract component descriptions
to their lowest levels. It significantly improves the search process if the
problem solver need to refine only one abstract component description at each
level.
3.4 Summary
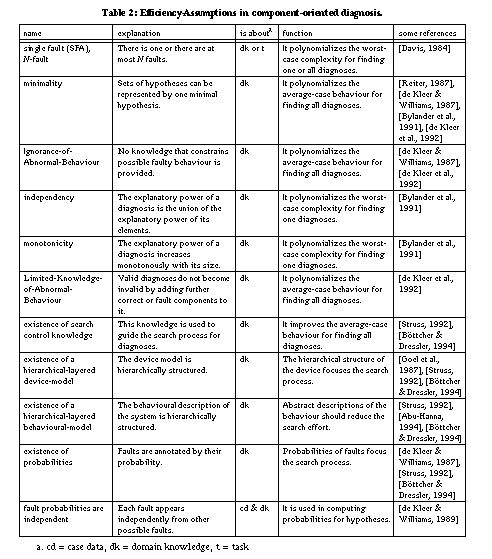
Figure 2 summarises the assumptions and groups them
according to their purpose. All these assumptions are introduced to reduce the
computational effort required to solve the problem. Table
2 provides an explanation of the assumptions along with the role they play
(function), the domain they are about (case data, domain knowledge or task), and
some references where they are discussed in more detail.
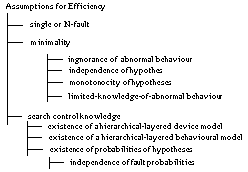
Figure 2 Assumptions for Efficiency
4 Efficient Interaction with the Environment: Hypothesis
Discrimination
Hypothesis discrimination
becomes necessary if the number of hypotheses found, exceeds the desired number
(cf. Table [Davis & Hamscher, 1988]). Additional
observations must be provided as the initial observations were not strong enough
to discriminate between existing hypotheses. Assumptions related to this activity
include the following (see Table [Benjamins, 1993]). First,
it must be possible to obtain additional observations. Examples of more
specific versions of this assumption are: can the device be unfastened, are
measuring points reachable, can components be replaced easily to test behaviour,
can new input be provided to the device, etc. Second, assumptions can be made
about the utility of additional observations. One can assume cost
information of additional measurements and knowledge about their discriminatory
power (i.e., knowledge about dependencies between hypotheses) to optimise their
selection. Again, NP-hard problems arise if one tries to optimise these
decisions. Therefore, assumptions concerning heuristic knowledge that
guide this process are necessary.
All these assumptions are necessary to optimise the
cooperation of the diagnostic system with its environment. In principle, one
could assume that all observations that are possible are provided to the system
before it starts its diagnostic reasoning. However, collecting observations is
often a major cost-determining factor. Therefore, assumptions are introduced
concerning the efficiency of gathering information with minimal costs.
5 The Role of Assumptions in Specifying Knowledge-Based
Reasoning Systems
In [Fensel et al.,
1996], we provided different aspects of a specification of knowledge-based
system which are related by assumptions (see Figure 3): a
task definition defines the problem to be solved by the knowledge-based
system; a problem-solving method defines the reasoning process of the
knowledge-based system; and a domain model describes the domain
knowledge of the knowledge-based system.
Figure 3 The different elements of a specification of a knowledge-based system
The task definition specifies the goals
that should be achieved in order to solve a given problem, which are functionally
specified as an input-output relation. A task definition also defines assumptions
about the domain knowledge. For example, a task that concerns the selection of
the maximal element of a set of elements, requires a preference relation as
domain knowledge. Assumptions are also used to define the requirements on such a
relation (e.g. transitivity, symmetry, etc.).
assumptionsdomain-knowledgeThe formula states that, if the assumptions on domain knowledge hold in the initial state, then the problem-solving method must terminate in a state that fulfils the goals of the task, if the assumptions on the task are fulfilled. This formula could be weakened by either strengthening the assumptions on domain knowledge (i.e., the problem-solving method must behave well for less initial states) or strengthening the assumptions on the task (i.e., the problem-solving method must achieve the goal in less terminal states).([problem-solving method] assumptionstask
goal)
The description of the domain model introduces the domain knowledge as it is required by the problem-solving method and the task definition. Three elements are needed to define a domain model. First, a description of properties of the domain knowledge at a meta-level. The meta-knowledge characterises properties of the domain knowledge. It is the counterpart of the assumptions on domain knowledge made by the other parts of a KBS specification: assumptions made about domain knowledge by these parts, must be stated as properties of the domain knowledge. These properties define goals for the modelling process of domain knowledge in the case of knowledge acquisition. The second element of a domain model concerns the domain knowledge and case data necessary to define the task in the given application domain, and necessary to carry out the inference steps of the chosen problem-solving method. The third element is formed by external assumptions that link the domain knowledge with the actual domain. These external assumptions can be viewed as the missing pieces in the proof that the domain knowledge fulfils its meta-level characterisations.
The assumptions of the different parts of a KBS specification define their proper relationships and the adequate relationship of the overall specification with its environment. Their detection, verification, and validation is an important part for developing correct reasoning systems. In [Fensel et al., 1996], we used the Karlsruhe Interactive Verifier (KIV) [Reif, 1995], developed in the specifications. Besides verification, KIV was used to detect hidden assumptions which were necessary to relate the competence of a problem-solving method to the task definition. Hidden assumptions could be found by analysing failed proof attempts. The analysis of partial proofs gives some hints for the construction of possible counter examples, but also for repairing the proof by introducing further assumptions. These assumptions are the missing pieces in proofing the correctness of the specification. Verifying these specification is therefore a way to detect underlying hidden assumptions.
6
Conclusion
It is essential to know the underlying
assumptions of a reasoning system in order to know when it is applicable.
Moreover, assumptions are good ways to characterise them and they can be used to
guide the acquisition process of domain knowledge. They define the type of
knowledge and its properties as it is are required by the reasoner.
In future work we will use the assumptions
identified in this paper to construct, in an assumption-driven manner, efficient
knowledge-based reasoners. We will also investigate whether the identified
assumptions can be structured in a such a way that they support this process. In
other words, we are looking for libraries of reusable assumptions. Still, our
current work suffers from serious shortcomings. We have not provided a proper
definition of the term
assumption nor a real justification for the
classification we applied in the paper. The assumptions where collected as they
could be found in papers on model-based diagnosis but it lacks a
theoretical-based framework that would allow to detect gaps in this list and to
decide when a level of (relative) completeness is achieved.
References
A. Abu-Hanna: Multiple
Domain Models in Diagnostic Reasoning, PhD thesis, University of Amsterdam,
1994.