Specification and Verification of Knowledge-Based Systems

Dieter Fensel¹, Arno Schönegge², Rix Groenboom³, Bob Wielinga¹

¹ University of Amsterdam, Department SWI
Roetersstraat 15, 1018 WB Amsterdam, the Netherlands,
E-mail: {fensel | wielinga}@swi.psy.uva.nl

² University of Karlsruhe, Institut für Logik, Komplexität und Deduktionssysteme
76128 Karlsruhe, Germany.
E-mail: schoeneg@ira.uka.de

³ University of Groningen, Department of Computing Science
P.O. Box 800, 9700 AV Groningen, the Netherlands.
E-mail: rix@cs.rug.nl

Abstract. The paper introduces a formal approach for the specification and verification of knowledge-based systems. We identify different elements of such a specification: a task definition, a problem-solving method, a domain model, an adapter, and assumptions that relate these elements. We present abstract data types and a variant of dynamic logic as formal means to specify these different elements. Based on our framework we can distinguish several verification tasks. In the paper, we discuss the application of the Karlsruhe Interactive Verifier (KIV) for this purpose. KIV was originally developed for the verification of procedural programs but it fits well for our approach. We illustrate the verification process with KIV and show how KIV can be used as an exploration tool that helps to detect assumptions necessary to close the gap between the task definition and the competence of a problem-solving method.

1 INTRODUCTION

During the last years, several conceptual and formal specification techniques for knowledge-based systems (KBS) have been developed (see Fensel & van Harmelen (1994), Fensel (1995c) for surveys). The main advantage of these modelling or specification techniques is that they enable the description of a KBS independent of its implementation. This has two main implications. First, validation and verification of the functionality, the reasoning behavior, and the domain knowledge of a KBS is already possible during the early phases of the development process of the KBS. A model of the KBS can be investigated independently of aspects that are only related to its implementation. Especially if a KBS is built up from reusable components (based on libraries of problem-solving methods, Breuker & van de Velde (1994), Benjamins (1993); and domain ontologies, Wielinga & Schreiber (1994)) it becomes an essential task to verify whether the assumptions of such a reusable building block fit to the actual provided task and knowledge. Second, such a specification can be used as golden standard for the validation and verification of the implementation of the KBS. It defines the requirements the implementation must fulfil.

The work that is presented in this paper provides three contributions to the field.

(1) We will develop a conceptual and formal framework for the specification of KBSs. The conceptual framework is developed in accordance to the CommonKADS model of expertise (see Schreiber et al. (1994)) because this model has become widely used by the knowledge engineering community. The formal means applied are based on combining variants of algebraic specification techniques (see Bidoit et al. (1991)) and dynamic logic (see Harel (1984)). We could not completely rely on existing specification languages for KBS since most of them cover only a subset of a complete specification of a KBS or lack from a appropriate semantics and axiomatization.

(2) We identify several proof obligations that arise in order to guarantee a consistent specification. The overall verification of a KBS is broken down into five different types of proof obligations that ensure that the different elements of a specification together define a consistent system with appropriate functionality.

(3) We show how the Karlsruhe Interactive Verifier (KIV) (see Reif (1995)), developed in the area of program verification, provides support in proceeding these proofs. Our view of verification is not restricted to the task of decorating software with a verified stamp after its construction. We believe that verification techniques can be valuable already in the development process (cf. Ledru (1994)). Especially in the context of the development process for KBS as proposed here we think of detecting (hidden) assumptions of PSMs by analysing failures of proof attempts.

The paper is organised as follows. In section 2, we discuss the different elements of a formal specification of a KBS and which kinds of proof obligation arise in their context. In section 3 we introduce an example of a task definition. We discuss the task of selecting a best explanation in abductive diagnosis. In section 4, we provide the definition of the weak PSM hill-climbing that finds a local optimum. We will then discuss in section 5 how ontology mappings and additional assumptions relate the task description with the competence of hill-climbing. In section 6 is shown, how the Karlsruhe Interactive Verifier (KIV) can be used for these verification tasks. We demonstrate termination and equivalence proofs and show how KIV can be used as an exploration tool that helps to find the appropriate assumptions necessary to link a competence of a PSM with a task definition. Section 7 summarizes the paper and defines objectives for future research.

2 A Formal Framework for the Specification of Knowledge-Based Systems

During the following, we first introduce the different elements of a specification. Then we discuss, how they are related and which proof obligations arise from these relationships.

2.1 The Main Elements of a Specification

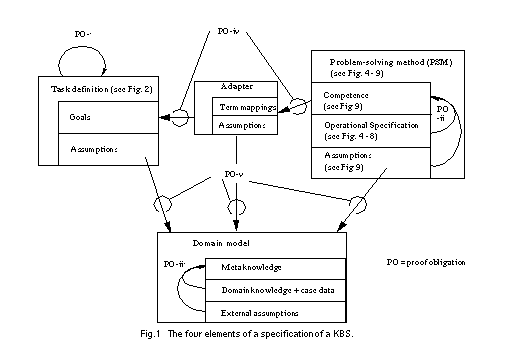
A framework for describing a knowledge-based system consists of four elements (see Figure 1): a task definition that defines the problem that should be solved by the KBS; a problem-solving method (PSM) that defines the reasoning process of a KBS; and a domain model that describes the domain knowledge of the KBS. Each of these elements are described independently to enable the reuse of task descriptions in different domains (see Breuker & van de Velde (1994)), the reuse of PSMs for different tasks and domains (Puppe (1993), Breuker & van de Velde (1994), Benjamins (1993)), and the reuse of domain knowledge for different tasks and PSMs (cf. Top & Akkermans (1994), Wielinga & Schreiber (1994)). A fourth element of a specification of a KBS is an adapter that is necessary to relate the functionality of a PSM and the provided domain knowledge with the desired functionality as it is defined by the task definition. Additional assumptions have to be introduced and the different terminologies have to be mapped. The necessity of adapters arise from the reusability of the other building blocks of a specification. They must be adjusted to each other and to the specific requirements of a given application problem.

The description of a task specifies some goals that should be achieved in order to solve a given problem. This functionality is specified as a relation between input and output of a KBS. A second part of a task specification is the definition of assumptions over domain knowledge. For example, a task that defines the selection of the maximal element of a given set of elements requires a preference relation as domain knowledge. Assumptions are used to define the requirements on such a relation (e.g. transitivity, connexitivity, etc.). A natural candidate for the formal task definition are algebraic specifications. They have been developed in software engineering to define the functionality of a software artefact (cf. Bidoit et al. (1991), Ehrig & Mahr (1985), Wirsing (1990)) and have already been applied by Spee & in't Veld (1994) and Pierret-Golbreich & Talon (1996) for KBS. In a nutshell, algebraic specifications provide a signature consisting of types, constants, functions and predicates and a set of axioms that define properties of these syntactical elements.

The description of the reasoning process of the KBS by a PSM consists of three elements. First, the definition of the functionality of the PSM. Such a functional specification defines the competence of a PSM independent from its realization (cf. van de Velde (1988), Akkermans et al. (1993), Wielinga et al. (1995)). Again algebraic specifications can be used for this purpose. Second, an operational description defines the dynamic reasoning process of a PSM. Such an operational description explains how the desired competence can be achieved. It defines the main reasoning steps (called inference actions) and their dynamic interaction (i.e., the knowledge and control flow) in order to achieve the functionality of the PSM. Dynamic logic (cf. Harel (1984)) or temporal logic (see Treur (1994)) are required to specify the dynamic interaction of these inferences. The definition of such an inference step could recursively introduce a new (sub-)task definition. This process of stepwise refinement stops when the realization of such an inference is regarded as an implementation issue that is neglected during the specification process of the KBS. The third element of a PSM are assumptions over domain knowledge. Each inference step requires a specific type of domain knowledge. These complex requirements on the input of a PSM distinguish it from usual software products. Pre-conditions on valid inputs are extended to complex requirements on available domain knowledge.

The description of the domain model introduces the domain knowledge as it is required by the PSM and the task definition. Ontologies (i.e., meta-theories of domain knowledge) are proposed in knowledge engineering as a means to explicitly represent the commitments of a domain knowledge (cf. Top & Akkermans (1994), Wielinga & Schreiber (1994)). For our purpose, we require three elements for defining a domain model: First, a description of properties of the domain knowledge at a meta-level. The meta knowledge characterizes properties of the domain knowledge. It is the counter part of the assumptions on domain knowledge of the other parts of a specification. They reflect the assumptions of task definitions and PSM on domain knowledge. Second, the domain knowledge and case data necessary to define the task in the given application domain and necessary to proceed the inference steps of the chosen PSM. Third, external assumptions that relate the domain knowledge with the domain (i.e., the system model with the actual system). These assumptions link the domain knowledge with the actual domain. These assumptions can be viewed as the missing pieces in the proof that the domain knowledge fulfils its meta-level characterizations. Some of these properties may be directly inferred from the domain knowledge whereas others can only be derived by introducing assumptions on the environment of the system.

The description of an adapter maps the different terminologies of task definition, PSM, and domain model and introduces assumptions that have to be made to relate the competence of a PSM with the functionality as it is introduced by the task definition (cf. Fensel (1995a), Benjamins et al. (1996)). It relates the three other parts of a specification together and establishes their relationship in a way that meets the specific application problem. Each of the three other elements can be described independently and selected from libraries of reusable task definitions, PSM, and domain models. Their consistent combination and their adaptation to the specific aspects of the given application (because they should be reusable they need to abstract from specific aspects of application problems) must be provided by the adapter. Its assumptions are necessary as in general, most problems tackled with knowledge-based systems are inherently complex and intractable, i.e., their time complexity is NP-hard (Bylander (1991), Bylander et al. (1991), and Nebel (1996)). A PSM can only solve such tasks with reasonable computational effort by introducing assumptions that restrict the complexity of the problem or strengthen the assumptions over domain knowledge. In the following, we illustrate the adaptation of a PSM in accordance to a formal description of a task by introducing assumptions. These assumptions either weaken the task definition or introduce additional requirements on the domain knowledge that is expected by the PSM. In the first case, the task is weakened to meet the competence of the PSM and in the second case, the competence of the method is strengthened by the assumed domain knowledge.

2.2 The Main Proof Obligations

Following the development process for task and domain specific PSMs as proposed in this paper the overall verification of a KBS is broken down into five kinds of proof obligations (see Figure 1):

(PO-i) the consistency of the task definition ensures that a model of the task definition exist;

(PO-ii) the operational description of the PSM exhibits the functionality described in the competence theor. This proof obligation recursively returns for each inference action of a PSM;

(PO-iii) the internal consistency of the domain mode;

(PO-iv) under certain assumptions, the functionality described in the competence theory is sufficient for solving the task;

(PO-v) the domain model fulfils these assumption.

Notice that PO-i deals with the task definition internally, PO-ii deals with the task definition internally, and PO-iii deals with the domain model internally, whereas PO-iv and PO-v deal with the external relationships between tasks, PSM, assumptions, and domain knowledge. Thus a separation of concerns is achieved which contributes to the feasibility of the verification (cf. van Harmelen & Aben (1996)). The conceptual model applied to describe knowledge-based system is used to brake the general proof obligations into smaller pieces and makes parts of them reusable. As PSMs can be reused, the proofs of PO-ii does not have to be repeated for every application. Only when a new PSM is introduced into the library (cf. Puppe (1993), Breuker & van de Velde (1994)), these proofs have to be done. Similar proof economy can be achieved for PO-i and PO-iii by reusable task definitions and domain models. Application specific proof obligations are PO-iv and PO-v. The first links the competence of the PSM to the functionality of the task introducing some assumptions. PO-v ensures that the assumptions over domain knowledge are fulfilled.

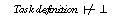
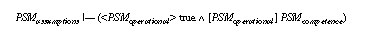
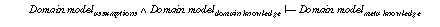
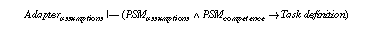
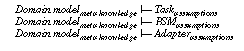
3 The Task ``Select A Best Explanation''

The task abductive diagnosis requires a set of observations as input and tries to deliver a correct, complete and most plausible diagnosis as output (see e.g. Bylander et al. (1991)). Roughly, one can identify three reasoning tasks of abductive diagnosis:

generating possible diagnoses;
testing whether these possible diagnoses are correct and complete;
selecting the diagnosis with the highest plausibility.

In the following we will focus on the third subtask selecting the explanation with the highest plausibility. The task assumes a set of correct and complete hypotheses for a given abductive problem as input. As output, it provides a diagnosis having the maximal plausibility.

Figure 2 defines the signature of the task under concern. The sort Hall defines the set of all possible hypotheses that can explain possible faults in the domain. The sort plausibilities is used to express the plausibility of a hypothesis. Hall and plausibilities must be data or knowledge types in the given domain and introduce ontological commitments. The function pl must be provided as domain knowledge. It relates hypotheses to their property that gets optimized.

The predicate hypothesis defines the set of actual hypotheses from which we search for the optimal element. The interpretation of the predicate hypothesis must be provided as data input to the task. The assumption over input is that it is not empty (see (3)).

A further predicate pref is required to distinguish between different elements of hypothesis by imposing an ordering in them. More precisely spoken, it is used to distinguish their values of the function pl. It defines an additional ontological commitment as this preference (i.e., the interpretation of the predicate pref) must be provided as domain knowledge. This semantical requirement for a preference relation must be further characterized by its properties. The precise definition of the preference predicate by axioms (4) - (7) defines requirements on the domain relationship that is used to interpret it. These axioms ensure that pref defines a linear ordering (sometimes also called total ordering).

We still have to define the functionality that should be provided by the task. That is, we have to define the predicate diagnosis with the predicate symbols hypotheses, pref and the function symbol pl. With axioms (1) + (2) we ask for a maximal element of the input as goal of the task.

4 The Weak Problem-Solving Method Hill-climbing

There exist several techniques (see e.g. Smith & Lowry (1990)) and PSMs (see Puppe (1993), Breuker & van de Velde (1994)) that are available to solve a given task. Three main decisions have to taken for deciding which problem-solving technique should be applied:

Is the problem-solving technique or method suitable for the given type of task and how large is the effort to map the terminology of the task onto the terminology of the method (Eriksson et al. (1995), Fensel et al. (1996))?
What types of domain knowledge are required by it? For example, a problem-solving method like propose & revise can only be applied to a parametric design problem if knowledge is available that can be used to propose initial parameter values and knowledge that can be used to repair constraints violations. Different variants of propose & revise can be identified by making these requirements on domain knowledge more precise Fensel (1995a).
How important and problematic is the efficiency aspect? Blind generate & test like methods have low efficiency but are easy to understand and implement. More sophisticated methods that compile test knowledge into the generate step provide higher efficiency but provide less understandability and require more effort in implementing and maintaining them (Davis & Hamscher (1992), Fensel & Straatman (1996)).

The main distinction between the algorithmic techniques of Smith & Lowry (1990) or so-called weak problem-solving methods (actually heuristic and non-heuristic search techniques, Bundy (1990)) at the one hand and problem-solving method at the other hand is that the latter make stronger commitments on the terminological structure of the tasks they can be applied to and the type of knowledge they require. For example, the task-specific board-game method is gained from the weak search strategy chronological backtracking by posing an internal terminological structure on the states of the search process and using this structure to define state transitions (Eriksson et al. (1995), Fensel et al. (1996)) that define stronger requirements on available domain knowledge.

Because for reasons of simplicity we have chosen a simple task definition, we can choose a weak problem-solving method for solving it. The task is a simple selection task where the elements are characterized by one property that should be optimized. We decided to choose the local search method hill-climbing for our example (cf. Figure 3). Hill-climbing is a local search algorithm that stops when it has found a local optimum.

The main requirement on domain knowledge that is introduced by hill-climbing (and by other local search methods) is the existence of a neighbourhood relationship between nodes (called graph during the following) that is used to guide the local search process. In general, several domain-specific possibilities exist to define such a graph relationship. In component-based diagnosis where each hypothesis is a set of defect components that explain the fault behaviour of a device this graph relation could be defined between two hypotheses by:

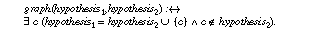
That is, the neighbour of a hypothesis are all hypotheses that contain one less defect component . It is clear that such a definition only makes sense if the preference of a hypothesis is related to the number of components it assumes to be defect. A further example for such a graph os provided in machine learning when one searches locally for rules or decision trees that cover a set of examples (cf. Quinlan (1984)). The graph relation is defined between rules that can be derived from each other by adding or deleting one premise. In general, hill-climbing can only be applied if a relation in the domain exist that can be used to define a graph for its search process.

One could argue why we do not just use a method that pairwise compares elements of the given set of hypotheses in random order as the complexity of the problem is only linear in the number of nodes. Still for large hypotheses sets, heuristic techniques must be applied. For example, the number of hypotheses increases exponentially in component-based diagnosis in the number of components (the set of hypotheses is the power set of the set of components). Therefore, efficiency of the search process becomes important and a heuristic approach is necessary.

In the following we provide the operational specification together with its knowledge requirements, the competence theory, and finally the proof obligations of this method.

4.1 Operational Specification of Hill-Climbing

Hill-climbing finds a local optimum. The entire method is decomposed into the following three steps. The inference action init selects the start node. An inference action generate generates all neighbours of a node. The inference action select selects the node with the highest value. Figure 4 gives the knowledge flow diagram of the method.

4.1.1 Inference Actions.

We use algebraic specifications enriched by the modality operators of dynamic logic to specify the functionality of inference actions. We distinguish between predicates that have the same truth values in the initial state and in the state after the execution of an inference action (called static predicates) from the predicates that change as a result of executing the inference action (called dynamic predicates). Figure 5 provides the definition of the three inference actions of the PSM. The functional specification is: extended by an operational specification (called implementation) that express the inference in a procedural way. We use a variant of dynamic logic for this purpose. The Modal Logic for Predicate Modification (MLPM) (see Fensel & Groenboom (1996)) was developed as a generalization of the specification languages KARL (see Fensel (1995b)) and (ML)2 (see van Harmelen & Balder (1992)). In addition, it provides an axiomatization that enables automated proofs. MLPM represents a state by the truth values of the predicates. An elementary state transition is achieved by changing the truth values of a predicate according to the truth values of a formula that is used to define the transition. Two different types of such elementary state transitions exist:

The e-operator expresses non-deterministic selection of one ground literal. A formula j can be used to restrict the set of possible ground literals from which one is chosen. All other ground literals of the predicate p are set to false. The l-operator allows updates of all ground literals of a predicate p according to the truth values of a formula j. All ground literals are set to true for which the according variable assignments evaluate the formula to true. All other ground literals of the predicate p are set to false.

MLPM provides the usual procedural constructs such as sequence, if-then-else, choice, and while-loop to define complex transition. We will make use of these constructs in section 4.1.4 when we define the operational specification of the entire hill-climbing method. As inference actions are regarded to be primitive they are defined by only one elementary transition.

An interesting feature of the inference action select is that it recursively repeats the definition of the original optimization task. In addition, select requires to find a global maximum (of all neighbourhood nodes) whereas the competence of hill-climbing can only guarantee to find a local one.

4.1.2 Dynamic Knowledge Roles

Dynamic knowledge roles (dkr) are means to represent the state of the reasoning process and are modelled by algebraic specifications (see Figure 6). Axioms can be used to represent state invariants. We define the requirement that the input provided to the method has to be non-empty.

4.1.3 Static Knowledge Roles

Static knowledge roles (skr) are means to include domain knowledge into the reasoning process of a PSM. Again, they are modelled by algebraic specifications. Axioms are used to define assumptions over the domain knowledge. Hill-climbing requires three types of domain knowledge. A preference is required to select an optimal neighbourhood node and a graph is required that defines the search space of hill-climbing, i.e. the neighbourhood relationship. The properties of this relation (i.e., the topography of the search space) heavily influence behavior and result of hill-climbing. Finally, knowledge is required that selects the initial node used to start the search process. The static knowledge roles are defined in Figure 7.

4.1.4 Control Flow

The operational description of a PSM is completed by defining the control flow (see Figure 8) that defines the execution of the inference actions. Again, we use Modal Logic for Predicate Modification (MLPM) (see section 4.1.1). An elementary state transition is achieved by changing the truth values of a predicate according to the truth values of a formula that is used to define the transition. Complex transitions are built up by defining procedural control (i.e., sequence, branch, and loop) on top of these elementary transitions.

The methods works as follows: First, we select a start node with init. If init fails to select a start node (i.e., no node in input is an element of the predicate start, see Figure 8), we randomly select one node from input for this purpose. After having selected this first node, a while loop is executed that stops when a local optimum is written to output. Within the loop we first generate all neighbours of the current node. If generate fails to generate new nodes (i.e., the current node has no neighbours) we are finished and write the current node to output. Otherwise, we select a best neighbour and compare it with the current node. If the best neighbour is better than the current node we use it for the next iteration of the loop. In the other case, we are finished and write the current node to output.

4.2 Competence Theory

The competence theory describes the functionality of the PSM. Again algebraic specifications enriched by the modality operators of dynamic logic can be used for this purpose (see Figure 9). As in the description of inference actions we distinguish static and dynamic predicates. The competence theory in Figure 9 defines that hill climbing is able to find a local optimum of the given set of elements.

4.3 Proof Obligations PO-ii

Does the operational specification of hill-climbing in section 4.1 have the competence as defined in 4.2 and can we guarantee termination of the method? Both proofs are sketched in section 6. Actually, several ``small'' errors were found in the original specification (compare section 5). As hill-climbing is a very simple PSM this illustrates the need for verification and tool support during this activity. As PSMs are designed for reuse these proofs need not to be repeated for every application. They have to be done only once when a PSM is added to a library of reusable PSMs.

5 Adapter: Linking the Task Definition with the Competence of the PSM

Linking a task definition and a domain model with a PSM requires two activities. First, the different terminologies have to be related (i.e., the different ontologies have to be mapped). Second, we have to relate the strength of the PSM with the desired goal of the task definition.

To relate the given task definition with the PSM, we have to relate the sorts Hall and plausibilities, the function pl, and the predicates hypotheses, pref, and diagnosis of the task definition (see Figure 2) with the sorts nodes and pref-values, the function h, and the predicates input, pref, and output of the competence of the PSM (see Figure 9).

The PSM hill-climbing has the competence to find a local optimum in a graph. The task under concern requires to select an optimal element from a set. In general, there are two possible strategies to close this gap (see Benjamins et al. (1996)). One can introduce additional requirements on domain knowledge that enable hill-climbing to find a global optimum or one can weaken the task definition. The first type of assumptions is expressed by formulas over the terminology as it is defined in static knowledge roles and dynamic input knowledge roles of the PSM. Static knowledge roles define the requirements for domain knowledge. Assumptions that weaken the task definitions are defined in terms of the task definition.

A trivial assumption which ensures that hill-climbing finds a global optimum is to require that each node is directly connected with each node.

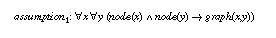
In this case, hill-climbing collapses to a complete search in one step as all nodes of the graphs are neighbours of each possible start node. If we would improve the init inference action we could weaken the assumption to: Every starting node must be connected with all nodes. The requirement on init would be to select such a node.

A less drastic assumption is to require that each node (except the maxima) has a neighbour with a higher preference.

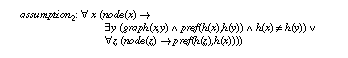
Actually, we will see that this assumptions is too weak to guarantee equivalence of task definition and PSM competence. One has to add an assumption over the input of the task (cf. section 6.3). We realized this as a result of applying the theorem prover KIV. The missing piece of the assumption was detected as a remaining open premise of an interactively constructed, partial proof that failed to show the equivalence of task definition and PSM competence.

The definition of the second if-then-else choice in Figure 8 is very critical for the competence of the PSM. Originally, we had the following definition (1):

As (1) can lead to infinite loops it was modified to (2) as an outcome of the termination proof.

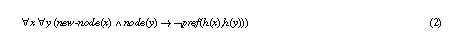
The disadvantage of (2) is that hill-climbing stops the search process when it reached a plateau in the search space (i.e., no neighbour node is better, only worse or equal neighbour exist). Therefore, an alternative solution would have been to work with condition (1) but introduce stronger requirements on the graph relation which guarantee termination of the PSM. If this relation does not contain direct or indirect cycles termination can be proven.

6 Verification with KIV

In software verification, tool support is extremely important. Large proofs and lemma bases with their (inter)dependencies have to be managed. Since in realistic applications correct programs (and specifications) are the exception rather than the rule, one has to keep track of (repeated) changes of lemmas and proofs. Thus, tool support for correctness management and reuse of proofs is necessary. Furthermore, the use of deduction systems permits to construct proofs substantially more accurate than can be done by hand. This increase in accuracy means an increase in reliability.

The KIV system (Karlsruhe Interactive Verifier) (see Reif (1992b)) is an advanced tool for the construction of provably correct software. It supports the entire design process starting from formal specifications (algebraic full first-order logic with loose semantics) and ending with verified code (Pascal-like procedures grouped into modules). It has been successfully applied in case-studies up to a size of several thousand lines of code and specification (see e.g. Fuch\xa7 et al. (1995)).

Our aim is to adapt the KIV system, originally designed for conventional software engineering, for development and verification of KBSs. For this purpose the KIV system is quite attractive. KIV supports dynamic logic which has been proved useful in specification of KBSs (cf. KARL, (ML)2, and MLPM). Since the deduction machinery of KIV is basically a tactical theorem prover (in the LCF-style Gordon et al. (1979)), it is prepared for extensions and modifications. KIV allows structuring of specifications and modularisation of software systems. Finally, the KIV system offers well-developed proof engineering facilities:

With the interactive proof environment even complicated proofs can be constructed.
A high degree of automation is achieved by a number of implemented heuristics.
Proof trees are visualized and can be manipulated with the help of a graphical user interface.
Generation of counterexamples for unprovable goals is supported.
An elaborated correctness management keeps track of lemma dependencies (and their modifications).
Automatic reuse of proofs allows an incremental verification of corrected versions of programs and lemmas (see Reif & Stenzel (1993)).

6.1 Applying KIV to the Hill-Climbing Example

In this section we report on results and experiences we gained in applying the KIV system to the hill-climbing example. Since we did not adapt the KIV system, we had to apply some small transformation on the formalization of hill-climbing. For example, dynamic predicates are modelled by variables and inference actions (init, generate, select) are represented by functions.

Figure 10 (which is original output from the KIV system using the graph visualization tool daVinci) shows how the modularisation facilities are employed. The actual algorithm is implemented in the hill-climbing-module (compare Figure 8). The inference actions are specified through axioms in the import of the module, i.e. in the specification actions (compare Figure 5, Figure 6 and Figure 7). The specification optimum corresponds to the competence of the hill-climbing method (compare Figure 9) and states that it computes a weak local optimum. Extra assumptions are needed to get the global optimum required in the task. The two assumptions from section 5 are introduced by means of the specifications totally-connected (assumption1) resp. better-neighbour (assumption2) which restrict the import (domain) of the method.

In KIV proof obligations (formulated in dynamic logic) ensuring that an implementation (module) meets its export specification are automatically generated. For the hill-climbing-module these obligations are termination of the hill-climbing algorithm and its partial correctness with respect to the optimum specification (i.e., proof obligations PO-ii of section 2.2). The module total-module contains the proof obligation that total connectedness of the graph implies that the local optimum is also a global one (i.e., PO-iv of section 2.2 using assumption1). The other module better-module contains the corresponding obligation for the assumption, that every node except the global maximum is connected to a better node (i.e., PO-iv of section 2.2 using assumption2).

6.2 Verifying the PSM Hill Climbing

The obligations for the hill-climbing-module correspond to proof obligation (PO-ii) from section 2.2. Both, termination and partial correctness (i.e. hill-climbing yields a local optimum, if terminating) were proved within the KIV system. For the termination proof it is shown that the number of nodes in the input set that are strictly better than the selected node decreases in each iteration. The proof of partial correctness was done by induction on the number of iterations necessary to terminate. Necessary for succeeding with these proofs was the introduction of the requirement that ensures non-emptiness of the input of the method. The introduction of this requirement was a result of our proofs. In addition, several errors in our original specification were found concerning the case when the inference actions init and generate do not provide output (the start predicate is not defined for the input of the PSM or the current element of node has no neighbours).

Figure 11 is a screen dump of the KIV system when proving the termination of the PSM hill-climbing. The current proof window on the right shows the partial proof tree currently under development. Each node represents a sequent (of a sequent calculus for dynamic logic); the root contains the theorem to prove. In the messages window the KIV system reports its ongoing activities. The KIV-Strategy window is the main window, which shows the sequent of the current goal, i.e. a open premise (leaf) of the (partial) proof tree (here goal number 2). The user works either by selecting (clicking) one proof tactic (the list on the left) or by selecting a command from the menu bar above. Proof tactics reduce the current goal to subgoals and thereby make the proof tree grow. Commands include the selection of heuristics, backtracking, pruning the proof tree, saving the proof, etc.

6.3 Verifying Assumptions and Detecting Hidden Assumptions

The obligations for the total-module (assumption1) and the better-module (assumption2) correspond to proof obligation (PO-iv) from section 2.2. It has to be proven whether the competence of the PSM fulfils the task definition by introducing assumptions. The proof obligation for assumption1 states that total connectedness of the graph (each node is directly linked with each node) implies that the local optimum is also a global one. Whereas this obligation has a rather trivial proof in KIV, the attempt at proving the obligation for the better-module failed, i.e. ends up with a remaining open premise (see Figure 12, the sequent window shows the unprovable premise). This result was a bit surprising for us. Supported by the graphical interface of KIV, interactively analysing the partial proof provides the explanation for the unexpected failure: the formula we wanted to prove was not true at all, i.e. the assumption that every node except the global maximum is connected to a better node, is not sufficient for the PSM hill-climbing to find a global optimum.

The analysis of the partial proof gives some hint for the construction of possible counter examples, but also a hint on how the assertion could be repaired. Here it leads straightforwardly to a strengthening of the assumption: the ``better node'' has to be member of the input of hill-climbing (cf. the sequent in Figure 12). That is, the assumption over the domain knowledge that is provided by the relationship graph must be supplemented by an assumption over the actual input of the PSM. Only if a better neighbour as required by assumption2 is an element of the actual input the equivalence can be proven.