Ghassan Beydoun and Achim Hoffmann
School of Computer Science and Engineering
University of New South Wales
Sydney, NSW 2052, Australia
Email: {ghassan,achim}@cse.unsw.edu.au
10 November 1997
This paper proposes a new approach to the design of intelligent systems. A new framework is used in which the specification of the actual system is sought to be an interactive process taking place directly between the knowledge acquisition system and the domain expert. The need for a mediating knowledge engineer is reduced to an initial domain modelling stage. Furthermore, the interactions necessary between the expert and the KA system take place at a level that is as intuitive as possible to the expert.
The emphasis of the types of systems we are addressing are KBS where search is an integral part of the problem solving process. Clearly defined combinatorial optimisation problems mark one end of the spectrum. The other end of the spectrum is marked by reducing the search process to just a single step, i.e. this covers also classification tasks. Intermediate problems being addressed are problems whose solution is probably best found by substantial search, however, where the criteria for an acceptable or even the best solution are difficult to define at the drawing board. Thus, the criteria for defined and refined during the initial use of the system. Our approach targets at the implicit representation of the less clearly definable quality criteria by allowing the expert to limit their input to the system to explanations of the steps in the expert search process. The explanations are used to construct a knowledge base representing search control knowledge. We are acquiring the knowledge in the context of its use, which substantially eases the knowledge acquisition process.
In its early days, AI had a strong emphasis on search methods. The perception was, that clever search techniques would account for most intelligent activities. While certain knowledge was necessary in order to formalise a problem properly, once it is formalised suitable search techniques would be applied to obtain a solution. Later, in the seventies a shift of emphasis in AI research took place, when researchers realized that in many cases it is not search which warrants the solution but rather the knowledge one has about the world and about how to solve specific problems. As a consequence the era of knowledge-based systems and expert systems began. Newell [Newell, 1982] suggested the notion of knowledge level, i.e. the idea to specify all necessary knowledge a system needs, at a level which, roughly speaking, corresponds to the level at which humans communicate their knowledge to their fellows. This idea penetrated much of the work what followed in the area of knowledge acquisition and expert systems.
On the one hand, the idea of the knowledge level itself received attention, resulting in developments such as a finer categorisation of knowledge into domain knowledge, problem solving knowledge etc, each type of knowledge describing different aspects of what a human problem solver or expert may use. On the other hand, also the techniques necessary to use the provided knowledge and to turn it into a working system received substantial attention in research. Earlier work on generic tasks is found in [Chandrasekaran, 1986]. I.e. it has been realised, that not simple generic techniques such as deductive reasoning techniques, or forward and backward chaining suffice to utilise knowledge in order to address all sorts of problems. Rather, specific techniques for different kinds of problems are necessary in order to build relatively complete and competent systems.
This line of research resulted in collections of problem-solving methods to be used in conjunction with domain ontologies as well as the relevant domain knowledge. See, e.g. [Puppe,1993, Schreiber & Wielinga,1994, Benjamins, 1995, Motta & Zdrahal,1996]. The idea of using domain ontologies aims at reusing part of the domain knowledge in different systems. I.e. a domain is characterised by a set of objects which are referred to by a set of terms which are deemed relevant and which can be used by different systems to handle different types of tasks. The development of reusable ontologies seems to incur the problem that such a general-purpose ontology will be very rich, while for a particular task only a small part of it will actually be needed. It seems to be a necessity to compensate for that by carefully choosing a suitable problem-solving method and by adapting the used ontology and to acquire the domain knowledge.
Furthermore, for search-intensive domains, it seems difficult to
have a sufficient repertoire of problem-solving methods available which
allows efficient search in a given domain.
Search can generally be reduced by taking specific characteristics
of the domain and the task in hand into account.
I.e. the problem-solver![]() has to be adapted to the domain and task in hand.
This is generally a non-trivial problem as it is often not obvious how
to search efficiently in a given domain.
has to be adapted to the domain and task in hand.
This is generally a non-trivial problem as it is often not obvious how
to search efficiently in a given domain.
In this paper, we propose a framework for integrating all of the above. I.e. the choice of a suitable problem-solving method as well as the acquisition of the necessary domain knowledge and the adaptation of a problem solving method to the resulting task-specific problem solver to ensure efficient and effective search. The reason why we believe this is possible is the following: Human experts are usually well capable to conduct a highly efficient search for a solution. Furthermore, they can take care of a large number of frame conditions just implicitly by directing their search towards search states which obey those conditions. E.g. in chess experts have normally problems to list all the aspects in a position they seek to optimise and to explain how they deal with trade-offs among these aspects. However, they take these issues implicitly into account when searching for a move by only considering a few of the possible moves at any search state.
I.e. instead of asking an expert to state all necessary conditions and optimisation criteria for a solution of a stated problem, then choosing a problem-solving method to subsequently run the problem-solver for a while to find some solution, we are proposing the following:
Let the system observe the expert's `manual' search for an overall solution and let the expert teach the system to conduct a search process automatically which simulates as close as possible the expert search process.The formalisation of the quality measure of potential solutions is effectively omitted.
The way we approach this is roughly as follows: In an initial phase, a basic domain ontology is developed (or reused) in order to define the search space. The search space should correspond to the possible states that an expert may encounter on their way to a problem solution. I.e. for all possible search actions an expert may decide to take, a corresponding search operator must be defined. Then an expert will sit in front of the system and perform a manual search for a `typical' task. For each search step the expert takes, the system will ask for an explanation that will lead the system to conduct the same search process as the expert. Whenever the system would take another search step according to its search rules, it will ask the expert for an explanation resulting in a possible exception to the system's current search rules, etc.
The paper is organised as follows: In the following section, we view problem solving as a search process, we also present our system SmS and indicate how it can be used to develop highly optimised problem solvers for specific domains and classes of tasks. In section 3, we discuss how SmS adapts itself across domains. In section 4 we sketch how SmS can be applied in parametric design and in particular we outline how SmS can be used to solve the Sysiphus II task of elevator design. Section 5 sketches how SmS has been used to acquire search knowledge in the domain of chess. Section 6 contains the conclusions of the paper and indicates future research.
In section 1, we discussed the efficiency of the human search method. Works like [Laird et al.,1993, Newell & Simo,1963] are inspired by this human search.
In [Fensel et al.,1997] Fensel discusses the notion of usability and reusability tradeoff. Using this notion we can group the solutions of automating search heuristics into three groups. The first group relies on strong problem solving methods and produces task dependent solutions such as Chinook [Shaeffer ,1992], or CAD tools [Gero ,1994], ... which are not reusable for other domains. The second group of work relies on weak problem solving and produces task-independent solutions to a set of domains, but uses knowledge acquisition to bridge the gap to a given domain, such work includes ASK [Gruber ,1989] and Theresias [Davis,1976]. The last group uses very weak problem solving and also produces task-independent solutions for a wider set of domains. This last group is harder to reuse. Its reuse requires lots of knowledge engineering to make the system usable for a domain. This last group includes systems like SOAR [Laird et al.,1993], GPS [Newell & Simo,1963], and Prodigy [Veloso et al.,1995].
Our system SmS matches systems in this last group in its generality. However, it is much easier to reuse as we will see. In particular, the expert explanations are given in domain terms, unlike other knowledge-based generic problem solvers [Yost, 1993]. When a domain ontology is available, SmS's reuse does not require a knowledge engineer.
SmS (Smart Searcher) was first introduced in [Beydoun & Hoffmann, 1997, Beydoun & Hoffmann, 1997] as a workbench to simulate human search processes. SmS is a generic problem solver which can be tailored for a given domain with relatively little effort. This is done by (re-)using a domain ontology while acquiring human expert knowledge. Using this acquired domain knowledge, SmS adapts the problem-solver to the domain on hand. SmS deals effectively with search problems as its knowledge base guides its search engine through the search space emulating the expert search process. SmS can also be used for classification tasks because the search process in SmS involves a classification task as a filter for determining suitable search steps. For a search degenerated to just one search step, search turns into classification. The classification tasks may also involve the acquisition of additional information from the user or other sources, before a classification can be made. This can be accommodated by SmS by a search through the state space, where specific search operators may requested the desired information and result in a corresponding new state in the search space. The view of SmS as a powerful general problem solver will be presented in the following section. But first, we will discuss the knowledge representation - Nested Ripple Down Rules - used to store the search knowledge, and then describe its integration in the SmS architecture in details.
In this section, we give an overview of Nested Ripple Down Rules, which represent a substantial extension to Ripple Down Rules, as introduced by Compton et al., see e.g. [Compton et al., 1992], Nested Ripple-Down Rules (NRDRs) were first introduced by Beydoun and Hoffmann in [Beydoun & Hoffmann, 1997]. NRDRs represent a powerful framework for the incremental development and maintenance of complex knowledge bases without a knowledge engineer.
The original conception of Ripple Down Rules (RDRs) allows the incremental definition of a concept by an expert as follows: Initially, a default class is given, which applies to all objects and forms the root of a decision tree which will represent the final concept definition. The expert monitors the application of the concept while objects are considered by the system. When the expert disagrees with the system's classification of an object x, he/she will give the system an explanation for why x needs to be differently classified. This explanation is a conjunction of one or more conditions being met by x, where each condition is a specified value range for one of the object's attributes. This explanation is transformed into an exception rule r, i.e. a branching condition, to be appended to the terminal node n, which gave the incorrect classification The object x becomes a cornerstone case for the rule r. For later amendments, this cornerstone case will be recalled to support the expert in providing conditions for further exception rules. Due to the fact, that each amendment to the tree has only local effect, i.e. changes only the classification of those objects, which are passed down that particular path, the tree always classifies those objects correctly, which have already been seen by the expert. In practice it turned out, that this approach allows an expert to easily specify conditions which characterise necessary exception rules fairly well and with minimal effort. Furthermore, possible mistakes in the specification of such rules are easily corrected later on. Compare also [Shiraz & Sammut,1997].
NRDRs work as follows: For explaining the classification of an object, we allow besides the choice of an attribute value range also the use of other user-defined concepts. In fact, those other concepts are also incrementally defined as a Ripple Down Rule. Since our approach results in the definition of a hierarchy of concepts, each represented by a (Nested) Ripple-Down Rule, this framework is called Nested Ripple Down Rules (NRDRs). Allowing the expert to define a hierarchy of concepts seems for the acquisition of search knowledge absolutely indispensable, since experts use abstract concepts to explain their way of searching a problem space. In search domains, the `raw representation' of the search space and a particular search state is usually too primitive to allow a suitable description of the expert's knowledge.
So using NRDR, the expert is able to give explanations using domain terms. This gives SmS a large advantage over other universal problem-solving architectures like TAQL [Yost, 1993] , where the explanations are given in computational model terms that require the domain expert to have programming skills. The integration of NRDR within the SmS architecture and the knowledge acquisition process is discussed in the next sub-section.
In this section we first give an overview of the system's architecture. This is followed by a detailed description of each module. The reuse of every module will also be discussed.
In designing SmS, we aimed at providing a workbench to allow the efficient development of search heuristics and their easy refinement. Thus, SmS aims towards providing means to acquire human expert search knowledge. For the acquisition of this knowledge and to assist the human expert in modifying the knowledge base as required, SmS models the structure of expert search processes as seen in Figure 1.
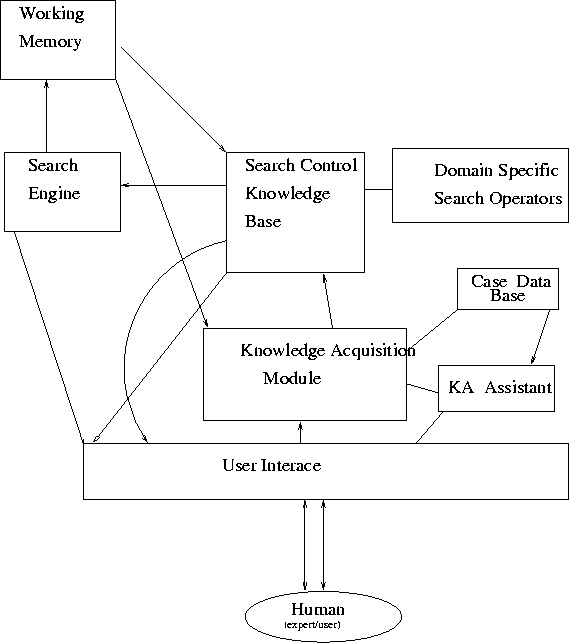
Figure 1: The architecture of SmS
To achieve SmS' goals, the Knowledge Acquisition Module together with the Case Database and the KA Assistant are responsible for the incremental development of an NRDR knowledge base which is always consistent with the seen cases. The Search Engine and the Working Memory are conducting the actual search. Which search states are visited is determined by the Domain Specific Search Operators Module and the Search Control Knowledge Base, which functions as a filter on all applicable search operators. The progress of the search is stored in the working memory. This progress is often used by the expert to explain his/her decisions.
We now give a more detailed description of every module in the system and comment on its flexibility as the system is used across different domains.
In addition, they allow tactical relations between squares and pieces to be stated. We will talk more about these primitives and their construction in section 5. These primitives are the only non-reusable components of SmS' architecture.
In the next section, we will outline how the above components can be reused across domains in the light of using SmS as general problem solver.
In this section, we will discuss how SmS works for different types of problems. This functionality is based on a controlled search. The degree of control of this search depends on the type of problem addressed.
The idea that search is a universal problem solving mechanism is not new. All that is required to formulate a search problem is a set of states, a set of operators, an initial state and a goal criterion. However, search problems stated in this way often lead to exponentially growing search time, see e.g.[Pearl & Korf,1989]. To contain this complexity, effective search procedures are needed which will usually be strongly tailored towards the problem domain in hand. The development cost of such highly specialised search procedures is usually high and the re-usability is limited. In SmS, the search procedure becomes the operationalisation of the acquired human expert search knowledge.
While search control knowledge acquisition, the expert assigns a weight to every rule, which he/she enters. This is a new extension to RDRs. While searching, the search engine applies the search operators with the highest weight. If the highest weight of an operator falls below a given threshold, the search engine backtracks and tries to find another state of the search tree, where an operator can be applied with a higher weight. So SmS uses an implicit evaluation function constructed during the knowledge acquisition process. I.e. the evaluation function is only implicitly contained in the search knowledge. By not pursuing certain search options, these search states are implicitly evaluated less worthy than those which are pursued.
SmS' search engine cooperates with the knowledge base to execute a directed search within a search graph. The knowledge base stores the human expertise. This expertise is used to filter through to the search engine only those state transition operators that are deemed most likely to yield a solution path. For a classification task, the filtered operators themselves become the class and the search graph is degenerated to only one node. This node describes the class of the search state. The term search state can be interchanged with the term "case".
Configuration tasks can also be viewed as search tasks. Thus, SmS is a flexible tool, which allows solving search problems, configuration tasks and classification tasks. Furthermore, by changing the domain specific search operators module in the system, which is the only domain dependent module, one can solve any problem of the three mentioned types. This module contains the domain dependent operators and ontological units that the operators act on. Coming up with the right operators and the ontological units for a given domain is a modelling task. This modelling task is normally needed when building classifiers with tools such as C4.5 [Quinlan,1993], RDR [Compton & Jansen, 1990], or Induct [Gaines,1991].
The modelling task of designing the operators and the ontological units is a knowledge engineering task accomplished by interviewing an expert. For example, in chess, the ontological units used consist of the 64 squares on the board and the pieces. The search operators are all the legal moves applicable to a position - these are computed by a custom build C procedure; although in principle could also have been designed by the expert. There are three types of primitive predicates from which other predicates can be defined by the expert. One primitive predicate measures the number of rows between two squares, a second primitive predicate measures the number of files between two squares and the third type of primitives counts the number of legal moves required for one piece to move from one square to another square.
These predicates are part of the interaction language that the expert uses to construct rules in the knowledge base. The language construct allows variable instantiation on the squares, and universal and existential quantification of the operators. Further, negation of the predicates, conjunction and disjunction between predicates are provided. The nested Ripple Down Rule used allows introduction of new terms into the language. This adds another dimension of flexibility to the language, and hence to the system.
From the above discussion and adopting Fensel (et al)'s [Fensel et al.,1997] viewpoint of problem solving methods, that problem solving method are search engines adapted to a given domain, the adaptation in SmS across domains takes place in the following ways:
The following section outlines how the SmS architecture can be used to solve the VT elevator problem. which is also known within the knowledge acquisition community as Sysiphus II. This problem provides a well-known example of a parametric design problem. Fensel (et al) [Fensel et al.,1997] present a detailed sketch of parametric design. Briefly, the design problem is to define values for a given set of interdependent parameters for which values must fall within given ranges and satisfy certain constraints given as a specification for the sought solution.
Yost and Rothenfluh [Yost & Rothenfluh, 1996] outlined a solution for the VT elevator problem. In this section, we will adapt some of their modelling and outline how it can be mapped to SmS.
The bulk of the effort in adapting SmS to the problem will be in designing the Domain Specific Operators Module. In particular, most of the effort is spent on designing the primitives needed by the expert to describe a class of search states and selector conditions for a search operator. Much of this section discusses the design of these operators.
The state generator generates all possible immediate states reachable from the given state. So we need to design all the operators which can transform a given search state. To do this we must consult with an elevator configuration engineer. The VT configuration task has operators of two types: One type for choosing model components and one type for adjusting design dimensions and weights.
The component selection operators are simple to design. They are based on the set of models available for every required component. However, the model used for a given component may depend on the models of several other components. For example, we need an operator to change the model of the cross-head of the elevator car. However, the model for the cross-head depends on the model of the sling (a vertical metal slab in the car). Therefore, the operator changing the model of the cross-head would also change the model of the sling.
As for the operators changing the dimensions and the weights, their design will include physical laws relating a subset of parameters involved. For example changing the counterweight would change the hoist cable tension and may require changing the car guide-rail unit. Furthermore, such operators changing the numerical values must generate states that are different from the given state on the design specification or component selection level. For instance, changing the counterweight by ten pounds does not cause any difference to the capacity of the lift in number of people, so the operator changing the counterweight adds/subtracts weight in 200 pound units.
When the operators are ready, we can build the state generator. The search state generator will be used to generate a search tree where a branch in the tree will correspond to an operator execution. The constraints of the values must be passed to the state generator as parameters to limit the search states to those acceptable values. For example, the sling under-beam space must be at least 2 inches, it would be pointless to generate any search state violating this value.
Once the state generator and the search operators are in place, the expert develops a knowledge base to guide the search within the defined search space. This knowledge base would classify which search states, to be generated by applying a given search operator, are worth pursuing in a given search state.
The knowledge base is incrementally developed using a Ripple Down Rule based representation [Compton et al., 1992]. In SmS the case representation includes all the primitives describing the current state and the state transition operator which led to this state because this operator description is often needed by the expert to explain the current state. For the VT problem we describe a case by a vector describing the 199 parameters and the last operator executed which led to this case. We must also provide the expert with primitives, which he needs to explain relations between the vector components of a case. For example, for the VT problem we need primitives stating the model of the engine, the number of loadable people required, primitives comparing different tensions etc. Any higher order description of a search state such as Excessive_Tension, Engine_Too_Small, can be accommodated using Nested RDRs as it is done in SmS [Beydoun & Hoffmann, 1997].
A typical knowledge acquisition session may start with a case where the elevator car is big enough for ten people but the engine is too weak and the specification requires ten people. So, he may enter a rule: "If Engine_Too_Small then Engine_Upgrade". Using Nested RDR, the expert extends the domain description language by defining the term "Engine_Too_Small" as separate RDR tree. The expert may then meet a case where the car is too small, but the engine has enough power. He then would add the following rule: "If Car_Too_Small then Car_Enlargement". This second rule would be attached to the false link of the first rule.
For explaining his/her search path, an expert will often need to refer to the search history within the same session. SmS allows this by storing the ongoing search in the working memory.
In this section, we demonstrate SmS' problem solving capability in the domain of chess. The associated knowledge acquisition cycle is shown. SmS interacts with a club chess player to develop a search knowledge base which produces a search process that resembles a human expert search process as much as possible. To do that, the expert defines concepts which approve moves to be considered in a min-max tree search, which in turn determines the actual move to be taken. While it seems, that the min-max search requires a specialised search mechanism, it can be accommodated in SmS by the letting the expert specify rules for move selections which take already into account that the game is a zero-sum game. I.e. each encountered search state provides the information of the relative gain or loss compared to the initial search state (the initial board position in which SmS has to decide on a move) as an extra attribute. In order to keep the searched tree small, it is important to approve only those moves which are really worthwhile considering any further. On the other hand, no critical move on either side should be excluded from the tree search in order to ensure high quality play. The knowledge acquisition process attempts to develop a concept `good move', which applies to exactly those moves which should be considered for the tree search. Initially, no search operator in any search state will qualify, i.e. no move in any chess position will be classified as `good move' and, hence, no tree search takes place.
In figure 3 there is a pawn to be captured on e3. Our human expert considers and even plays for black Nd5xP. The expert considers it as a good move because he wins a piece, i.e. the pawn.
Figure 2: Graphical view of the knowledge base. Concept definitions are given in
separate windows.
He introduces a new rule "If WinPiece then Good". Subsequently, he needs to explain the meaning of the newly used attribute "WinPiece" in the form of a new RDR for which the expert enters "If WinPawn then WinPiece" as a root node. Similarly for "WinPawn".... Eventually, the concepts are defined in domain-dependent primitive terms, which are supplied to the system as C-functions. Now, assume it was white's turn, and white played Re1. SmS1.2 considers Ne3xP as a good move because it wins a piece [ because it wins a pawn]. The expert disagrees with this because Ne3xP is not a safe move as the black knight on e3 can be captured by a rook on e1. So the knowledge base must be modified. At this point, there are three rules available for modification. At the highest level, the expert can add "If not SafeMove then Not Good" on the true link of "If WinPiece then Good". Or, he can change the meaning of "WinPiece" by adding "If not SafeMove then Not WinPiece". Finally, he can also change the meaning of "WinPawn" in the "WinPiece" Ripple Down Rule tree by adding "If Not SafeMove then Not WinPawn". The choice of the point of modification is part of the knowledge acquisition process. These choices are made known to the expert by a hierarchical interface (see figure 2). In this particular example any of the modifications is valid. The expert chooses the last option.
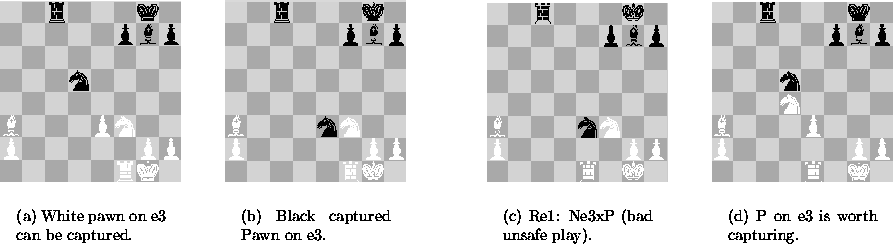
Figure 3: Black to play. Free pawn on e3.
Chess is a two players game. The search tree nodes alternate for the two players. To look ahead further than one half move, the knowledge base must be large enough to account for the responses of the opponent. The expert plays for white explaining the option he takes. Thus, for figure 3(a) the expert plays Re1 to protect the pawn on e3, and for figure 3(d), he plays Bb2 to protect the knight on d4. The knowledge base is developed by the expert's input. The concept of "DefendingPiece" is introduced. As for black's sake who is required to find some good moves in the absence of possible killer moves, i.e. capturing and/or exposing white's pieces, the knowledge base is extended to cover more strategic moves such as strengthen one's defence or attack. As a result, in our knowledge acquisition session, our knowledge base evolved to 20 rules and 11 concepts, with a depth of the concept hierarchy of up to four. In position 4(a) with white to play, the evolved knowledge base leads to a tree search of depth five involving 47 nodes. This is opposed to the blind min-max tree search of several million of nodes for this position. The pruned tree reflected largely the expert's decisions on which moves are worthwhile to investigate further. The computer play with a pruned tree of depth three is also shown below figure 4. The play shown resulted in the computer gaining the upper hand against an average human player.
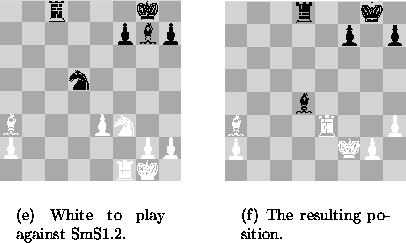
Figure 4: a) and b): Average human player against our system SmS1.2.
Left: Starting position. After the move sequence of
1. Re1 Rd8
2. h3 Bf6
3. Nd4 Nxe3
4. Rxe3 Bxd4
5. Ke2 ...
the right position was reached.
In this paper we presented a new general framework for problem-solving. We had a particular emphasis on search-intensive problems. However, we argued that even problems like classification tasks fit into the framework, which involve virtually no search at all. While we are promoting a knowledge acquisition method based on Ripple-Down Rules, we approached the problem class of parametric design from a different angle as in [Compton et al.,1998]. In [Fensel ,1997] it was suggested to adapt a given problem solving method to a given domain and task. In our approach we took the extreme view by having just a single generic problem solver for a large class of search problems. The `adaptation' to a particular domain and task occurs during the knowledge acquisition process. The unique feature of our approach lies in the fact that we seek a different type of knowledge from an expert which encompasses all knowledge that is needed: We ask for a detailed explanation of the expert's search process for a problem solution - regardless whether this is a search-intensive domain or rather a strongly constrained domain, which would require an extensive knowledge acquisition session to formalise all the relevant constraints. In our approach we do not distinguish between these types of knowledge, as the constraints are implicitly obeyed by the expert's search process. Our knowledge acquisition takes place in the context of the actual use of the knowledge being specified by the expert. Previous experiments with acquiring classification knowledge in the context of its use has been highly successful [Compton et al.,1993]. Thus, we believe that the acquisition of search knowledge in the context of its use will be similarly effective in the general case and, as a consequence, that the general framework for problem-solving presented in this paper is widely applicable.