The major focus of recent knowledge acquisition research has been on problem-solving methods (PSM). This paper present results where a PSM developed for classification has been extended to handle a configuration or parametric design task, designing ion chromatography methods in analytical chemistry. Surprisingly good results have been obtained seemingly because any knowledge that has been added to the knowledge base, has been added precisely to overcome any limitations of the PSM. These results suggest a trade-off between domain knowledge and the power of the PSM and that greater use of domain knowledge would facilitate re-use by allowing PSMs to be used for a broader range of tasks.
The
critical insight with the emergence of knowledge based systems (KBS), was the
usefulness of knowledge as compared to pure search. This was formulated in
ideas such as the "knowledge principle". This resulted in expert system shells
which while specifically intended for the accumulation of knowledge as rules,
also allowed developers great flexibility in the way they organised domain and
problem solving knowledge (e.g. OPS5 (Brownston, Farrell et al. 1985) ). As
fairly general purpose programming tools, these shells suffered from difficult
maintenance problems like any other software (Bachant and McDermott 1984;
Compton, Horn et al. 1989). Certainly, the modularity of rules allowed rules
to be very easily added to such systems, but the addition of new rules
invariably affected the prior performance of the system. Simply because a rule
could be added in a modular fashion, gave no guarantee that it would not have
other changes on the system apart from those intended. To deal with this
problem, the research area of verification and validation emerged.
On approach to this problem was to control the way in which rules were
added to minimise the impact on the system's performance (Compton and Jansen
1990). However, the major research focus in KBS development since the mid
80's, has been in attempting to understand these systems at the knowledge level
and thereby develop more principled approaches to development. The knowledge
level perspective points out that there is a whole level of inquiry about how
domain knowledge is reasoned with to solve a problem a opposed to the content
of the domain knowledge itself. If one goes back and considers earlier
rule-based systems, one finds embedded in the knowledge base all sorts of
different methods, or model-construction operators (Clancey 1992). The classic
example of this, is the practice in MYCIN to put the conditions in a rule, in
order of importance. There was no indication in the knowledge base for why
this was done, but in fact, it was to ensure that the most significant data was
dealt with first and that any questions asked of the user reflected this. The
MYCIN backward chaining inference engine processed rule conditions in order of
appearance in the rule. The aim of knowledge-level modelling has been to
improve maintenance and re-use of PSMs by making such mechanisms explicit. The
principle focus in this has been on tasks and then PSMs; i.e. what is the best
way to reason with domain knowledge to find a solution to a particular type of
problem. There have been many ways of designing, developing, organising and
accessing PSMs, with the most influential of these from the mid-80's probably
being the KADS methodology (Wielinga, Schreiber et al. 1992). For reviews and
frameworks for understanding these modelling approaches see for example:
(Brazier and Wijngaards 1997; Fensel, Motta et al. 1997). More recently
ontologies have become a more major focus of knowledge-level modelling . If
one considers ontologies in terms of Brachman's earlier work (Brachman and
Schmolze 1985), it is fair to say that the present emphasis is on the T-Box,
that is on definitions of terms and their relationships in an inheritance
hierarchy. The other aspect of Brachman's perspective, the A-box, assertional
knowledge, e.g. rules about the domain, is of little interest at present in
knowledge acquisition (KA) research. From a knowledge-level modelling
perspective, the content of the assertions in assertional knowledge is not part
of the knowledge level and so is of little interest. However, the question in
this paper is whether in practice there is a trade-off between PSM power and
assertional knowledge about objects and properties in the domain. The
assertional knowledge the expert is asked to provide is simply to identify the
appropriate solution for a particular problem and identify the features of the
situation which lead the expert to choses this particular solution, or
component of the solution.
There has always been interest in flexible KBS where the reasoning of the
system can adapted to the current problem e.g. (Brazier, Treur et al. 1995).
However, more recently there has been an upsurge in interest in providing some
more generic framework for understanding PSMs and their relationships. Fensel
has developed a way of seeing PSMs as adaptations of each other (Fensel 1997).
Perkuhn groups PSMs in terms of family resemblances (Perkuhn 1997).
Significantly the core viewpoint in (Fensel, Motta et al. 1997) is that PSMs
are search engines, but adapted to the particular task in hand. There is
nothing novel in saying that PSMs are generalised search engines, however the
historical evolution of this emphasis is of interest. AI started off with
search methods. It was then realised that knowledge overcame many of the
limitations of pure search. However, the use of knowledge was somewhat
inchoate and a knowledge level perspective emerged to try to make sense of the
use of knowledge. We are know back at a focus on search, but on understanding
PSMs as different types of search, and the relationships between them related
to the difference in search. The hypothesis in this paper is that there is
advantage in continuing the cycle and returning to an emphasis on the notion of
the utility of domain knowledge to reduce search. Although this knowledge
reduces search, as will be seen, the domain expert is simply providing advice
as to why a particular solution should be chosen in a particular context.
Finally in this perspective on PSMs, Beys sees PSMs as ways of mapping
input sets to output sets (Beys and van Someren 1997). Again it is not novel
to suggest that PSMs map inputs to outputs, however this re-emphasis at this
stage is of interest. Beys uses a set based approach because of its
mathematical utility. Our perspective is more simple in that essentially a KBS
is a system that produces some form of output given some form of input and the
output produced for any given input is the same as would be produced by an
expert. The most primitive form of mapping between input and output is simply
to connect inputs to the appropriate output, with every feature of the input
being taken into account. This would be clearly inefficient as there would be
no generality. If we consider a flat rule structure where a rule makes a final
conclusion from the initial data, then rules are a mapping from input to output
but where only the salient features in the case are identified. This provides
greater generality but with this goes a greater liability for error when the
generalisations are over-generalisations. If one then moves to something like
heuristic classification, one attempts to provide some abstraction of the data
and then rules relating to these abstractions. This is a further attempt at
generalisation, or rather an attempt to minimise the amount to knowledge
required and make use as much use of possible of knowledge added - essentially
increasing the range in which given knowledge will be used. This attempt to
increase the power of the knowledge by increasing the scope of where it might
be used, again increases the possibility of errors (causing the maintenance
problems we have already noted). Heuristic classification can be seen as a
form of local search. Given some data there are other facts that can be
concluded on the way to a solution. However, the facts that can be concluded
will depend on both the knowledge available in the rules and the inference
mechanism; how the conflict resolution strategy works and so on. If one moves
to a more complex example such as the Propose and Revise PSM (Marcus and
McDermott 1989; Zdrahal and Motta 1994) we have a system where there is some
form of local search (propose), but when this develops a solution or partial
solution that is not allowed because of some constraint, there is a mechanism
to modify the current solution (i.e. to jump to some other part of the search
space) and start the local search again. This can again be seen as a way of
trying to generalise, or rather minimise the amount of knowledge required. The
system is not provided with sufficient knowledge so that a local search will
necessarily provide a solution. Rather when the local search fails the system
is designed to jump to another part of the search space, to see if a solution
can be found there. That is, it is trying to make the best use of the
knowledge available.
Denoted by Dk = {<pi, vij>}, where pi [element] P and vij [element] Vi a
configuration. This results in the following definitions:
We believe that this categorisation of knowledge follows from a Propose and
Revise type of perspective. Certainly it also applies to other PSMs (Motta and
Zdrahal 1996), but we would see these attempting the same types of advantage
from generalising knowledge (or rather attempting to minimise the domain
knowledge required) as Propose and Revise. As far as we can see there is no
need to invoke a notion of constraint knowledge unless, one is planning on
responding differently to a constraint violation than to an unsatisfied
requirement. Similarly there is no need to understand requirements and
preferences differently unless wishes to reason about them differently. The
reason for requiring constraint type knowledge is to be able to test if
constraints are satisfied and judge whether the search needs to be started in a
new part of the space. If one considers problems simply in terms of mappings
from inputs to outputs, then in parametric design tasks, the expert's core
competence is simply in indicating what components are required in the solution
for the given input and what features in the input indicate that these
components are required. We also implicitly include in this, the notion that
the expert will also provide information on when a solution is inappropriate
for the given input and why a different solution is appropriate. A particular
solution may be required or preferred because it satisfies constraints or is
preferred over another solution, but in the situation the expert's judgement is
simply that the features in the input indicate a particular solution is
appropriate. Of course the expert may reflect on what he has done is all sorts
of ways and provide all sorts of explanation, but his or her core competence is
identifying features in the input which determine the output.
This then raises the question of a trade-off. Clearly one should attempt
to make as much use of the knowledge available as possible. For example in
Propose and Revise, if a solution is not found by some form of local search,
the search is moved to another part of the space. On the other hand one can
attempt to overcome the problem by adding further knowledge so that the problem
is found by local search. In other words, for a parametric design problem, can
a problem solver be developed by adding knowledge so that local search will
always provide a solution, without a revise step? A similar approach was used
in (Gaines 1992) where an assignment problem was solved by classification, but
there was not the same emphasis on simplifying the search required by use of
domain knowledge. Clearly it is likely that such a solution will probably
require a greater amount of domain knowledge. On the other hand,
generalisation produces errors and maintenance problems and in particular,
despite its ability to move to new parts of the search space, Propose and
Revise may not be very satisfactory at finding solutions (Zdrahal and Motta
1996). Zdrahal and Motta's solution (ibid) to this problem was to locate the
search in an appropriate part of the space by using case-based reasoning. This
is essentially an attempt to provide a solution by adding more domain
knowledge. It is also an attempt to avoid the maintenance problems of dealing
with the domain knowledge in the system, by providing another source of domain
knowledge used in a different way.
The
aim of this study is explore whether the addition of further domain knowledge
can be used to extend the competence of a problem solver. This would also
provide a significant contribution to the reuse possibility of PSMs as it would
suggest that simpler PSMs could be used for more complex tasks. We have
another underlying aim of extending Ripple Down Rules (RDR) to construction
tasks, and in the first instance configuration tasks. RDR are a way of
building knowledge based systems which focus on very simple addition of domain
knowledge. The major success of RDR has been in single classification tasks.
A challenge to RDR from the PSM community has been to extend RDR to a wider
range of tasks than classification. As will be discussed below RDR have been
extended to multiple classification tasks. They have also been used by others
for control tasks (Shiraz and Sammut 1997) and for heuristic search (Beydoun
and Hoffman 1997). This paper describes the extension of RDR to a
configuration task. The advantage of RDR for exploring the trade-off
hypothesis is that they facilitate knowledge acquisition and a trade-off
between domain knowledge and PSM power can only be useful if domain knowledge
can be added as required to enable the problems solver to find a solution.
Any RDR development depends on there being a sequence of cases which can be
used to develop a system, so that RDR studies have generally been closely tied
to specific applications. There is also little interest in developing RDR
systems where there is not a genuine expert amiable. With other methods the
knowledge engineering needs to study and understand the domain regardless of
whether or not there is an expert. A consequence of this is that a knowledge
engineer will make significant progress to at least developing a problems
solver and framework for the domain knowledge without an expert to provide the
knowledge. In contrast with RDR, after some fairly simple data modelling,
there is no other task except for the expert to identify the features in the
data for a case which indicate the appropriate solution. For this reason we
did not attempt the Sisyphus II project. The application here is to develop an
adviser for Ion Chromatography (IC) methods. The major advantages of this
domain for this project is that we had access to a large database of cases as
well as one of the world's experts on IC, and as well a there is real need and
considerable interest from analytical chemists and equipment suppliers in
developing such a system. IC is widely used as a standard tool to separate and
thereby identify charged components of a solution, for example in pollution
studies. The sample is injected onto a column and washed through with a
solute. Different ions in the sample are retarded in their passage through the
column. Factors affecting separation include: charge on the solute,
polarizability of the solute and ion-exchange capacity of the stationary phase,
hydrophobicity of the polymer used in the stationary phase, hydrophobicity of
the solute, amount of organic material present, relative sizes of the solute
and the pores of the stationary phase etc. Clearly, ion chromatography methods
will vary with the composition of the sample being investigated and there are a
number of different components of an IC method that have to be selected. The
configuration task is to select an appropriate set of components and conditions
to be able to measure the substances of interest in the sample at hand. This
is a difficult task, and the last author has assembled a data base of some 4000
methods as a resource to assist in method selection for difficult problems.
The particular sub-domain covered in the system developed so is Ion Exclusion
Chromatography. Ion Exclusion Chromatography is concerned with separating
acids and bases; however, exactly the same considerations, and the same range
of options in configuring a method apply. In the cases covered to date by the
system, separation of up to 16 different components is required.
The following contains a more detailed discussion of RDR, the Ion
Chromatography domain, the RDR Configuration method and results of using this
method on the IC domain.
Ripple
Down Rules (RDR) is based on the idea that when a KBS makes an incorrect
conclusion the new rule that is added to correct that conclusion should only be
used in the same context in which the mistake was made (Compton and Jansen
1990). In practice this means attaching the rule at the end of the sequence of
rules that were evaluated leading to the wrong conclusion. Thus, this rule
will only be evaluated in the same context in which the mistake was made.
Rules are thus added when errors are made, allowing for an incremental,
maintenance-focussed approach to knowledge acquisition. Since rules are added
to correct the interpretation of a specific case, the system ends up not only
with a number of rules but with cases associated with these rules: the cases
that prompted the addition of the rule. This leads to validated knowledge
acquisition in that the new rule that is added should not be allowed to be
satisfied by any of the cases for which rules have already been added and for
which different conclusions are appropriate. These cases are already handled.
For single classification problems, where the system will output one of a
set of conclusions a binary tree structure is used and the new rule added after
the last rule evaluated. It is worth noting that the tree is extremely
unbalanced and resembles a decision list with decision list refinements rather
than a tree (Catlett 1992). With this structure the only case that can reach
the new conclusion is the case associated with the rule that gave the incorrect
conclusion. Implicit in this outline is a non-monotonic approach in that each
rule proposes a final conclusion to be output, unless this conclusion is
replaced by a later correction rule that fires. Rules are never removed or
edited, all errors are corrected by adding new rules.
A single classification RDR approach was used to build the PEIRS system for
pathology interpretation. This system was largely developed whilst in routine
use. Apart from the development of the initial domain model the knowledge base
was developed entirely by an expert without knowledge engineering support or
skills. The only task the expert had was to identify features in the case
which distinguished it from the case associated with the rule giving the wrong
conclusion and which was now being corrected. This allowed the expert to add
about 2400 rules at the rate of about 3 mins per rule and the system ended up
being in routine use for four years and covering about 25% of chemical
pathology (Edwards, Compton et al. 1993). This compares very favourably with
other medical expert system projects and with expert system projects in general
in terms of knowledge acquisition tasks. A range of studies have also been
carried out demonstrating that problems with repetition that may occur with
this approach happen less in practice than might be expected (Compton, Preston
et al. 1995; Compton, Preston et al. 1994).
The notion of repetition in the KB is an important one with respect to the
trade-off between knowledge and PSM power. The use of a binary tree structure
means that knowledge in one particular pathway is not accessible to a search
down another pathway. Repetition in single classification RDR occurs because
when a solution is not found down a particular path, further knowledge is added
to that path rather moving the search to elsewhere. However. as noted. in
practice the repetition is small, while the speed of knowledge acquisition with
a 'chunk' added every three minutes meets the requirements of the new DARPA
project on very large knowledge based systems. The requirement for this
project is for KBS with between 10,000 and 100,000 chunks of knowledge to be
built at this rate. PEIRS was only 2,500 rules, but the cost of knowledge
addition was close to constant as the KB grew, where the DARPA requirement is
close to linear with KB size, suggesting the DARPA requirement could be met.
For multiple classification tasks an n-ary tree structure was developed and
replaced the binary tree structure used for single classification tasks. With
this structure a rule may have many children and all children will be
evaluated. If any of these are satisfied all their children will be evaluated
and so on. In contrast for single classification, once a child rule was found
to be satisfied by the data, only its children were evaluated, and as soon as
of these were found to be true only the children of that rule would be
evaluated and so on. In MCRDR all immediate children are evaluated regardless.
We again have a simple non-monotonic system, where child conclusions replace
the parent conclusion. As a result of the n-ary tree structure, cases
associated with a number of other rules may reach a new rule being added. If a
new child rule is being added, the cases associated with its parents, siblings
and all the children of its siblings can all reach this rule, and so it must be
made specific enough to exclude any of these cases satisfying this rule. It is
assumed that all conclusions required are already provided by the KBS for these
cases.
The approach to validate knowledge acquisition was simply to show the case
to the expert and ask them to select features leading to the new conclusion.
If these features were present in any of the cases that could reach the new
rule, this case was also shown to the expert and the expert was required to add
further features to the rule to exclude this case. This process was repeated
until none of the 'cornerstone cases', cases associated with rules, were
satisfied by the rule. The cornerstone cases associated with rules include
the case for which the rule was added and also cases which correctly reach this
rule but were stored because they caused the addition of another rule.
Surprisingly even when up to 600 cases might reach the rule, the expert has to
see only two or three cases before a sufficiently precise rule is constructed
to exclude all cases. In various evaluation studies MCRDR has been shown to be
more efficient that single classification RDR even for single classification
tasks, but at the small cost of the expert having to deal with 2 to 3 cases for
each rule added (Kang 1996; Kang, Compton et al. 1995).
These parameters and values suggest about 1012 possible
configurations. No doubt, the space of real possibilities is far smaller than
this, but clearly the search space is quite sizeable.
As noted, in the approach adopted we do not indicate separately: constraints,
requirements and preferences. As will be seen, the expert simply indicates the
features in the case which indicate a particular configuration is appropriate.
Such rules can be considered as requirements. However, importantly, the
approach also requires the expert to add rules to correct inappropriate
configurations. Now these rules will still be requirement rules. However,
since they cause the replacement of certain components of the previously
proposed configuration, they also implicitly express constraints and
preferences. There is also no global cost function as similarly costs are
handled by the rules added.
A sample case for which the system may have to produce a method may look
like:
SAMPLE |
PHOSPHORIC |
ARSENIC(V) |
BORIC |
PKA |
2.13 |
2.19 |
9.24 |
CHARGE |
PNEG |
PNEG |
PNEG |
MW |
98 |
0 |
61.84 |
RI |
0 |
0 |
0 |
SPECT |
NO |
NO |
NO |
ELECTROACIVE |
. |
NO |
NO |
CONDUCTANCE |
. |
YES |
YES |
FORMCOM |
MOLYBD |
NO | |
H_STATE |
TRI |
MONO |
The sample may contain only a single substance of interest, but this is a
trivial case and of little interest. Here the sample contains three analyte
ions and the method should be able to separate them all. In another example ,
the acid/base components of interest in white wine would be: Lactic, Tartaric,
Malic, Acetic. In the cases considered to date separation of up to 16
components has been required. The system also contains a data base from which
the information in the lower panels of the table is derived, e.g molecular
weight, conductance etc. The development of this data base required a
significant effort and it strictly speaking it is an important part of the
problem solving. Initial attempts to develop a system, where components were
identified by name only, were not very successful, because experts, even if
only implicitly, reason about particular attributes of these components, and
different combinations of components result in different combinations of values
for these attributes. However, this database will not be considered further
here as the major issue is incremental addition of heuristic rules given an
appropriate data representation. Use of the data base corresponds to the
abstraction stage in heuristic classification. Here however, the abstraction
involved decomposition of what are essentially objects identified by a kind of
proper name into their significant and more generic components. It should be
noted that RDR do not claim to solve the problem of developing an appropriate
data model for the domain. This remains a standard knowledge engineering, or
rather software engineering task. However RDR do make this stage easier,
because of the ability to refine over-simplified abstractions with reference to
the raw data in local contexts (Edwards, Compton et al. 1993). Current
projects are aimed at developing a more general RDR based facility for refining
abstractions concurrently with knowledge that uses these abstractions.
The cases used in this study come from a data base of all the significant
Ion Chromatography methods published between 1980 and 1996, amounting to over
4000 cases. Of these a smaller subset of Ion Exclusion Chromatography cases
were selected These in fact comprised the first cases in the data base. An
initial study developed configurations for a group of 81 cases which were
referred to the last author for assessment. The assessment was simply on
whether these methods would work for the particular sample. The configurations
for a total of 361 cases were assessed by the first author as being equivalent
to the specific methods in the data base. This assessment was necessary
because often there are number of alternatives that will satisfy the same
constraints and the selection of a particular one is unimportant, probably
determined by what happened to be available in the laboratory. The second
author is a PhD student in Chemistry, but not an expert in Ion Chromatography.
His specific expertise in IC was developed during this project. He acted as
the expert in providing rules for the expert system and as well in deciding
that methods were adequate. Note that these two activities are integrated for
RDR, in that rules are only added when the expert believes the solution
presented is inadequate. The methods suggested for these cases will eventually
be assessed by a more experienced expert. However, for this study the level of
expertise is not of major importance. Note that the expert task here was not
in deciding on a method, but in the more generic 'expert chemist' task of
deciding whether a method proposed corresponded to a method in the data base
for the identical case. Secondly the 'expert' had to gradually assemble rules
to produce the specified method. It has previously been shown that RDR can be
successfully used with 'lesser experts'. A high level of expertise can be
achieved by the RDR system, but takes longer to develop as more correction
rules have to added to correct earlier poor rules (Compton, Preston et al.
1995; Shiraz and Sammut 1997). If then a rapid development of expertise can be
achieved with a PhD student expert, it is highly plausible that even better
performance will be achieved with a more experienced expert.
This
study follows an earlier project were machine learning was used to develop an
Ion Chromatography expert system (Mulholland, Preston et al. 1996). The 4000
cases were used to develop a series of classification knowledge bases each able
to decide on one of the components of the method given the other components and
the other data for the case. These knowledge bases were build by induction
with Gaines' Induct algorithm (Gaines 1991) being the method of preference
because of its superior ability to deal with classes with small numbers of
representatives.
Once these knowledge bases were developed the task was to develop a PSM
that could use this knowledge to find a suitable solution. The method arrived
at:
This problem solving method can be seen as a variant of propose and revise in
that the heuristic of only adding components of the solution to working memory
when only a single value for that component was possible, is a type of best
first search. That this will be changed if the same process arrives at another
conclusion corresponds to the revise part of propose and revise, This
essentially starts the search in a new place. Since the requirement to move
from one single conclusion to another is somewhat difficult to satisfy,
convergence is reasonably good and the system does not jump around too much.
The
machine learning based configuration system did not allow for incremental
knowledge acquisition. To develop this we first of all moved to MCRDR to allow
multiple conclusions. This did not offer any intrinsic advantage over multiple
single classification knowledge bases. However, the n-ary tree structure with
no false branches more transparently supported the possible requirement to
hypothesise conclusions.
Initial efforts were focussed on adding knowledge acquisition to the type
of PSM used for the ML configuration system but now applied to MCRDR. This
proved to be very complex and involved tracing inference sequences and adding
rules in such a way that the same inference sequence would be maintained for
any case. The inference sequences tended to be quite long. While this was
under investigation we attempted two simpler heuristics corresponding
approximately to a best first and a complete search.
Heuristic 1: (ROSE)
Heuristic 2: (SALMON)
We soon abandoned the SALMON strategy as too expensive and because ROSE was
surprisingly effective.
The final inference approach used is as follows.
The knowledge acquisition strategy used is:
Propose and revise methods typically contain a forward chaining rule
interpreter to cover the assignment of values to attributes, but then a process
to revise this and move to a different part of the state space if the local
search has reached an unsatisfactory solution. The central hypothesis here is
that when such the system reaches an unsatisfactory or incomplete solution, it
is better to add rules enabling it to find a solution rather than moving to a
different part of the search space. Here the revision does not take place by
moving to another part of the search space. Rather the domain knowledge is
revised at acquisition time to improve local search.
In this method new knowledge is added to the system so that the single
appropriate value for an attribute will be assigned. It is important to note
that this assignment cannot be replaced by another value due to the simple
addition of other rules to deal with other cases. Another rule firing will
result in multiple values for the attribute and so that nothing will be added
to memory for this attribute. For an alternate value to be assigned, a
specific refinement rule, either stopping or replacing the earlier assignment
has to be added, so that there will be only a single value for the attribute
from the new rule. We believe this is a critical feature in the success of the
approach. Also the knowledge acquisition ensures that as rules are added they
will not be satisfied by the cases for which other rules have been added.
Since configuration RDR depend critically on Multiple Classification Ripple Down rules, they are described here in some detail.
The
MCRDR is represented as an n-ary tree. The inference of MCRDR evaluates all the
rules in the first level of the KB, then evaluates the rules at the next level
of refinement for each rule that was satisfied at the top level and so on. The
process stops when there are no more children to evaluate or when none of these
rules can be satisfied by the current data case. If any child rule fires, its
conclusion replaces the conclusion of the parent rule. If more than one child
fires, the conclusions of these rules are also included as conclusions, but
perhaps to be replaced by conclusions from their children.
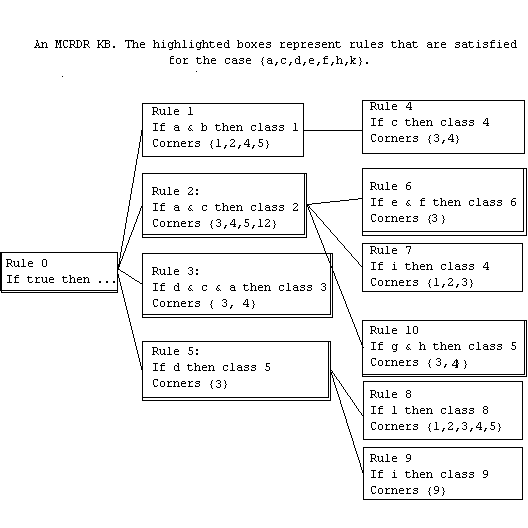
The inference process can be viewed as multiple paths from the root of the
KB to the conclusions, as shown below in Fig 2.

Path 1 [(Rule 0, ...), (Rule 2, Class 2), (Rule 6, Class 6)] Info 1 Path 2 [(Rule 0, ...), (Rule 2, Class 2), (Rule 10, Class 5)] Info 2 [4] Path 3 [(Rule 0, ...), (Rule 3, Class 2)] Info 3 Path 4 [(Rule 0, ...), (Rule 5, Class 5)] Info 4 [2]
When a case has been misclassified or a new classification is required, knowledge acquisition is needed. The process has three aspects: firstly, the system acquires the correct classifications from the expert; secondly, the system decides on the new rules' location and finally, the system acquires new rules from the expert and adds them to correct the knowledge base.
The expert simply states the new classifications. For example, if the system produces classifications class 2, class 5, class 6 for a given case, the expert may decide that class 6 does not need to be changed but class 2 and class 5 should be deleted and class 7 and class 9 need to be added.
The
system should find the locations for the new rules that will provide these
classifications. There are several possibilities that are shown in the table
below
Wrong classifications |
To correct the KB |
Wrong classification stopped |
Add a rule (stopping rule) at the end of path to prevent the classification (gives a null classification) |
Wrong classification replaced by a new conclusion |
Add a rule at the end of path to give the new X classification. |
A new independent classification |
Add a rule at a higher level to give the new classification. In practice MCRDR systems add rules for independent classifications only at the top level. |
With
MCRDR, a number of cases can reach a new rule and the higher in the tree the
more cases can reach the rule. The new rule should distinguish between new case
and all of these cornerstone cases. The cases that can reach a rule are those
associated with the parent of a new rule, its siblings and their children.
Note that the cases associated with rule include cases for which any rule is
added, but for which this rule gives a conclusion.
The algorithm for adding a new rule is as follows:
The same process is followed whether a stopping or refinement rule or new
top-level rule is added.
Some
sample rules follow. In the first a component of the configuration depends
only on the data supplied. In practise the PKA of the various ions in the
sample is derived from the data base and then rules can refer to these
abstractions of the data.
IF (MIN(PKA) >= 2.0) & (MAX(PKA) <= 4.0) THEN MOBILE_PHASE =
HCl
The following is a rule which has conditions derived from other components
of the configuration.
IF (DETECTOR= CONDUCT)&(MOBILE_PHASE = HCl) THEN SUPPRESSED= YES
The
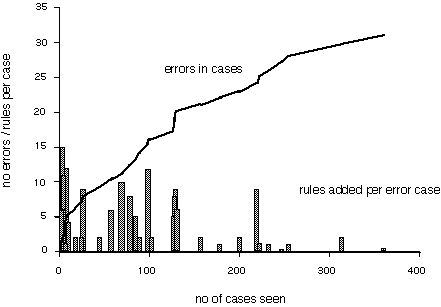
key feature of the results is that the rate at which errors are made on cases,
and therefore the rate at which rules have to be added, rapidly decreases.
Although the system has not been evaluated on a large independent set of cases,
the cases on which the system is tested here are random cases which have not
been preselected. They were in fact the first 361 Ion Exclusion Chromatography
cases chronologically in the data base. It is therefore reasonable to assume
that error rate on these cases should be an approximation of the error rate
more generally. Since errors are being corrected as they occur, the average
over any sequence of cases should be greater than the actual error at the end
of the sequence with the errors corrected. The error rate on the first 100
cases was ~17%, it was ~7% for the second 100 cases and <3% for the last 100
cases. This final error is after only 361 cases have been seen and 156 rules
have been added. The convergence for what might be assumed to be a difficult
configuration problem is quite remarkable. From experience with PEIRS and
other RDR systems, the system will never reach completion and rules will
continue to be added for cases throughout the 4000 in the data base. This is
also consistent with experience with machine learning, that knowledge in a
system is never complete (Catlett 1991).
That there are further errors to be corrected may seem to be a weakness of
the method. However, evaluation of expert systems always indicates some level
of error and the error here after only 361 cases is comparable to good final
error rates of other expert systems. The difference here however is that the
possibility of further errors is fully recognised and accepted and provision is
made for fixing these as they occur. Generally in conventional systems, the
published error rate is the final performance level of the system and there is
little facility for correcting errors except careful editing of the knowledge
base followed by separate verification and validation.
The second significant aspect of this development is the number of rules
that have to be added for each case corrected. In the initial stages rules
have to be added for virtually every component of a configuration. However as
the system develops, cases which require a lot of rules become fewer and fewer,
again showing the improvement of the system. Of interest, occasionally the
later cases require many rules, suggesting that these case are quite different
from those already handled. One would expect this phenomenon to continue, but
with decreasing frequency.
We have already argued that because of the type of expertise required in
developing this system that it was reasonable to use a Chemistry PhD as the
expert. A real expert will only produce a better system. We in fact provided
81 cases to the fourth author and developer of the IC data base. Of these 88%
of the methods were identified as workable and only 12% as not workable. The
main area of error was in choosing a mobile phase and showed up a weakness in
the second author's knowledge about the interchangeability of acids in IC.
This evaluation is not complete and it is therefore possible to raise
questions about the quality of the system as it develops further. It may also
be hypothesised that the search space in reality is far smaller than it seems.
All we can say is that this hypothesis conflicts with the experience of
analytical chemists in setting up Ion Chromatography methods for particular
samples. This is seen as difficult task where the average practitioner may
need expert advice or a series of false starts before an appropriate method is
set up. The next stage in this project is to distribute both a knowledge base
and tools for further knowledge addition to about six laboratories outside
Australia recognised internationally for their leadership in Ion
Chromatography. It seems unlikely that these laboratories would be keen to
participate if this was a small problem. Despite these indications to the
contrary we remain open to the suggestion that we have in fact provided a
solution to a small problem. However, it is also fair to say, that compared to
the level of evaluation available for other problem solving methods for
configuration tasks, configuration RDR is exceptionally well validated. One
may well ask for more validation of configuration RDR, but it would seem
unreasonable to argue that one should prefer other less well validated methods
because of the possibility that the validation of configuration RDR may not be
complete.
One significant conclusion from this study is that we have now shown that
the RDR incremental development approach can be extended to construction tasks.
This opens up the possibility of incremental knowledge acquisition for the
whole range of knowledge based system tasks. The next major issue in this
research is to integrate RDR and refining data models for a domain, rather than
data modelling being a conventional knowledge engineering exercise. A first
step in this is integrating a subsumption hierarchy and RDR so that changes to
neither the A-box or the T-box should degrade the performance of the system
(Martinez, Benjamin et al. 1997). As we have noted there is other independent
work on using RDR for control tasks and heuristic search. There have also been
a number of independent uses of RDR as representation in machine learning.
We believe the central issue raised by these results is the trade-off
between knowledge acquisition and problem solving. As Motta and Zdrahal noted
there is considerable variety in the various implementations of Propose and
Revise (Motta and Zdrahal 1996). This suggests that researchers were
attempting to come up with or tailor optimal PSMs for such problems. Most PSM
literature is written as if the domain knowledge is somehow available and the
issue is how to develop a PSM which can use this domain knowledge to find a
solution. We suggest that this leads to the idea, at least implicitly, that if
a PSM cannot find the solution, then a better PSM is needed. In contrast RDR
suggests that more knowledge should be added which the PSM can use to find the
solution. In RDR, when knowledge, relevant to the case in hand is not found,
rather than fix the PSM, more knowledge is added that can be found with the
given PSM.
The key question is whether this confers any advantage. On the face of it
the advantage is considerable. A configuration RDR PSM can be used for
multiple classification. There will simply be no inference cycles because
conclusions reached do not affect other conclusions reached. We have also
shown that single classification is better carried out with an MCRDR PSM. This
means that a single PSM can be used for these three tasks. No doubt a Propose
and Revise PSM could also be used for classification but there are major
differences in how knowledge is categorised in these methods. In heuristic
classification there is an abstraction step and then a refinement step. In
Propose and Revise there is both a local search step and a revision step moving
to another part of the space. There is also a clear distinction between the
knowledge used in the different stages. In contrast with RDR all knowledge is
simply an identification of salient features in a case which lead to a
particular part of the output required. There is no need to understand the
internal structure. However, the internal structure is virtually identical for
MCRDR and configuration RDR. The long standing of claim of RDR is that this
type of incremental validated knowledge acquisition is rapid and reliable and
something that can be carried out by an expert without the aid of knowledge
engineer. In this regard it is worth noting that neither the expert nor anyone
else in the project knows anything about the actual organisation of the
knowledge in the IC knowledge base.
The question for RDR of course remains whether RDR PSMs can be developed or
the current PSM extended to deal with still further KBS tasks. We ourselves
would see the extension to a configuration task as a major step in
demonstrating that they can be used for construction tasks. Secondly, we see
the present results as suggesting that perhaps these apparently more difficult
problems can be approached in much simpler ways if greater use is made of
domain knowledge. However, our own experience in developing such methods is
that progress is slow. Firstly RDR PSMs require the major extra feature that
they support incremental validated knowledge acquisition. However, the
problems in coming up with such PSMs were that we invariably attempted to
develop something that was far more complex than is actually required.
This work has been supported by an Australian Research Council Grant. The insightful and helpful comments of the anonymous referees are greatly appreciated although we doubt we have fully addressed the concerns they raised
Bachant,
J. and McDermott, J. (1984). R1 revisited: four years in the trenches. The
AI Magazine Fall: 21-32.
Beydoun, G. and Hoffman, A. (1997). Acquisition of search knowledge, in E.
Plaza and R. Benjamins (Eds.), Knowledge Acquisition, Modelling and
Management. Berlin, Springer. 1-16.
Beys, P. and van Someren, M. (1997). A systematic approach to the functionality
of problem solving, in E. Plaza and R. Benjamins (Eds.), Knowledge
Acquisition, Modelling and Management. Berlin, Springer. 17-32.
Brachman, R. and Schmolze, J. (1985). An overview of the KL-ONE knowledge
representation system. Cognitive Science 9(2): 171-216.
Brazier, F. and Wijngaards, N. J. E. (1997). An instrument for a purpose driven
comparison of modelling frameworks, in E. Plaza and R. Benjamins (Eds.),
Knowledge Acquisition, Modelling and Management. Berlin, Springer.
323-328.
Brazier, F. M. T., Treur, J., Wijngaards, N. J. E. and Willems, M. (1995).
Formal Specification of hierarchically (de)composed tasks. Proceedings of
the 9th Banff Knowledge Acquisition for Knowledge-Based Systems Workshop,
Banff, SRDG Publications, Dept. of Computer Science, University of Calgary.
25.1-25.20
Brownston, L., Farrell, R., Kant, E. and Martin, N. (1985). Programming Expert
Systems in OPS5. Reading, Mass, Addison-Wesley.
Catlett, J. (1991). Megainduction: A Test Flight. Machine Learning:
Proceedings of the Eighth International Conference.,
Morgan Kauffman. 596-599
Catlett, J. (1992). Ripple-Down-Rules as a Mediating Representation in
Interactive Induction. Proceedings of the Second Japanese Knowledge
Acquisition for Knowledge-Based Systems Workshop, Kobe, Japan, 155-170
Clancey, W. J. (1992). Model construction operators. Artificial
Intelligence 53(1-115):
Compton, P., Horn, R., Quinlan, R. and Lazarus, L. (1989). Maintaining an
expert system, in J. R. Quinlan (Eds.), Applications of Expert Systems.
London, Addison Wesley. 366-385.
Compton, P., Preston, P. and Kang, B. (1995). The Use of Simulated Experts in
Evaluating Knowledge Acquisition. Proceedings of the 9th AAAI-Sponsored
Banff Knowledge Acquisition for Knowledge-Based Systems Workshop, Banff,
Canada, University of Calgary. 12.1-12.18
Compton, P., Preston, P., Kang, B. and Yip, T. (1994). Local patching produces
compact knowledge bases, in L. Steels, G. Schreiber and W. Van de Velde (Eds.),
A Future for Knowledge Acquisition: Proceedings of EKAW'94. Berlin,
Springer Verlag. 104-117.
Compton, P. J. and Jansen, R. (1990). A philosophical basis for knowledge
acquisition. Knowledge Acquisition 2: 241-257. (Proceedings of the 3rd
European Knowledge Acquisition for Knowledge-Based Systems Workshop, Paris
1989, pp 75-89)
Edwards, G., Compton, P., Malor, R., Srinivasan, A. and Lazarus, L. (1993).
PEIRS: a pathologist maintained expert system for the interpretation of
chemical pathology reports. Pathology 25: 27-34.
Fensel, D. (1997). The tower-of-adaptor method for developing and reusing
problem-solving methods, in E. Plaza and R. Benjamins (Eds.), Knowledge
Acquisition, Modelling and Management. Berlin, Springer. 97-112.
Fensel, D., Motta, E., Decker, S. and Zdrahal, Z. (1997). Using ontologies for
defining tasks, problem-solving methods and their mappings, in E. Plaza and R.
Benjamins (Eds.), Knowledge Acquisition, Modelling and Management.
Berlin, Springer. 113-128.
Gaines, B. (1991). Induction and visualisation of rules with exceptions. 6th
AAAI Knowledge Acquisition for Knowledge Based Systems Workshop, Banff,
7.1-7.17
Gaines, B. (1992). The Sisyphus problem-solving example through a visual
language with KL-ONE-like knowledge representation. Sisyphus'91: Models of
Problem Solving, GMD (Gesellschaft fur Mathematik und Datenverarbeitung
mbH).
Kang (1996). Multiple Classification Ripple Down Rules. UNSW, PhD thesis.
Kang, B., Compton, P. and Preston, P. (1995). Multiple Classification Ripple
Down Rules : Evaluation and Possibilities. Proceedings of the 9th
AAAI-Sponsored Banff Knowledge Acquisition for Knowledge-Based Systems
Workshop, Banff, Canada, University of Calgary. 17.1-17.20
Marcus, S. and McDermott, J. (1989). SALT: A knowledge Acquisition Language for
Propose-and-Revise Systems. AI Journal 39: 1-38.
Martinez, R., Benjamin, R., Preston, P. and Compton, P. (1997). Integrating
Ontology Development and Knowledge Acquisition.
Motta, E. and Zdrahal, Z. (1996). Parametric Design Problem Solving.
Proceedings of the 10th AAAI-Sponsored Banff Knowledge Acquisition for
Knowledge-Based Systems Workshop, Banff, SRDG Publications, University of
Calgary.
Mulholland, M., Preston, P., Haddad, P., Hibbert, B. and Compton, P. (1996).
Teaching a Computer Ion Chromatography from a Database of Published Methods.
Journal of Chromatography 739: 15-24.
Perkuhn, R. (1997). Reuse of problem-solving methods and family resemblances,
in E. Plaza and R. Benjamins (Eds.), Knowledge Acquisition, Modelling and
Management. Berlin, Springer. 174-189.
Shiraz, G. and Sammut, C. (1997). Combining Knowledge Acquisition and Machine
Learning to Control Dynamic Systems. 15th International Joint Conferences on
Artificial Intelligence (IJCAI'97) 1997., Nagoya, Japan,
Wielinga, B. J., Schreiber, A. T. and Breuker, J. A. (1992). KADS: a modelling
approach to knowledge engineering. Knowledge Acquisition 4(1 (special
issue on KADS)): 5-54.
Zdrahal, Z. and Motta, E. (1994). An In-Depth Analysis of Propose and Revise
Problem Solving Methods. Proceedings of the Third Japanese Knowledge
Acquisition for Knowledge-Based Systems Workshop (JKAW'94), Tokyo, Japanese
Society for Artificial Intelligence. 89-106
Zdrahal, Z. and Motta, E. (1996). Improving Competence by Integrating
Case-Based Reasoning and Heuristic Search. Proceedings of the 10th
AAAI-Sponsored Banff Knowledge Acquisition for Knowledge-Based Systems
Workshop, Banff, SRDG Publications, University of Calgary.