1 Introduction
Most languages for knowledge acquisition, elicitation, and reasoning are in pure text format. Text presentation is easier for a computer program to process. However, text form presentation is not an easily understandable form, especially for those domain experts who are not familiar with computer programming. Visual representation of knowledge relies on graphics rather than text. Visual representations are more understandable and transparent than textual representations (Nosek & Roth, 1990).DESIRE (DEsign and Specification of Interacting REasoning components) (Brazier, Dunin-Keplicz, Jennings, Treur, 1995; Brazier, Treur, Wijngaards, Willems, 1996) is a development method used for the design of knowledge-based or multi-agent systems. DESIRE supports designers during the entire design process: from knowledge acquisition to automated prototype generation. DESIRE uses composition of processes and of knowledge composition to enhance transparency of the system and the knowledge used therein.
Originally, a textual knowledge representation language was used in DESIRE. Recently, as a continuation of the work represented in (Moeller, Willems, 1995) a graphical representation method for knowledge structures has been developed. A description of both graphical and textual representation of knowledge is given in Section 2.
Constraint Graphs (Kremer, 1997) is a concept mapping "meta-language" that allows one to visually define any number of target concept mapping languages. Once a target language is defined (for example, the DESIRE's graphical representation language) the constraint graphs program can emulate a graphical editor for the language as though it were custom build for the target language. This "custom" graphical editor can prevent the user from making syntactically illegal constructs and dynamically constraint user choices to those allowed by the syntax.
Constraint Graph's graphical environment is used to represent knowledge in a way that corresponds closely to the graphical representation language for knowledge that is used in DESIRE. A translator is described that bridges the gap between the graphical representation and the syntax of the textual representation language used in DESIRE.
2 Graphical Knowledge Representation in DESIRE
In this section both graphical and textual representations are presented for the specification of knowledge structures in DESIRE (Brazier, Dunin-Keplicz, Jennings & Treur 1995). Knowledge structures in DESIRE consist of information types and knowledge bases. In Sections 2.1 and 2.2 graphical and textual representations of information types are discussed. In Section 2.3 representations of knowledge bases are discussed.Information types (also called signatures) provide the ontology for the languages used in components of the system, knowledge bases and information links between components.
2.1 Basic concepts in information types
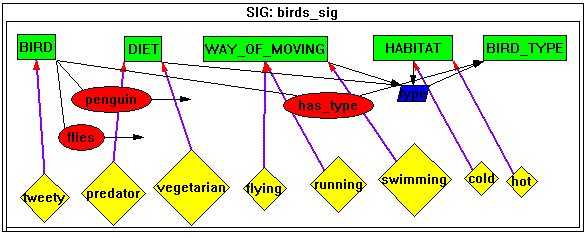
A sort can be viewed as a representation of a part of the domain. The set of sorts categorizes the objects and terms of the domain into groups. All objects used in a specification have to be typed, i.e., assigned to a sort. Terms are either objects, variables, or function applications. Each term belongs to a certain sort. The specification of a function consists of a name and information regarding the sorts that form the domain and the sort that forms the co-domain of the function. The function name in combination with instantiated function arguments forms a term. The term is of the sort that forms the co-domain of the function. Relations are the concepts needed to make statements. Relations are defined on a list of arguments that belong to certain sorts. If the list is empty, the relation is a nullary relation, also called a propositional atom. The information type birds is an example information type specifying sorts, objects, functions and atoms with which some knowledge concerning birds can be specified. The information type is specified graphically in Figure 2, and textually in Example 1.information type birds
objects tweety : BIRD; carnivore, omnivore, vegetarian : DIET;
cold, hot, coastal_areas : HABITAT; relations flies, penguin : BIRD;
|
2.2 Compositionality of information types
Compositionality of knowledge structures is important for the transparency and reusability of specifications. In DESIRE two features enable compositionality with respect to information types: information type references, and meta-descriptions. By means of information type references it is possible to import one (or more) information type(s) into another. Referencing is useful as it enables the definition of a generic relation on a sort (for which objects may not have been specified) in one information type, and the addition of objects, functions, relations, and sub-sorts to the sort in another information type. For example, information type birds above can be used in an information type that specifies a language for objects that might fly. Suppose that flying objects are either flying birds, flying insects, or flying machines. Given the information types birds, insects, and machines the more complex information type flying objects presented in Figure 3 and Example 2, can be constructed using information type references. Note that the sorts BIRD, INSECT, and MACHINE are specified to be sub-sorts of sort WORLD OBJECT.information type flying_objects
sorts WORLD_OBJECT; sub-sorts BIRD, INSECT, MACHINE : WORLD_OBJECT; objects ariane_5 : MACHINE;
hindenburg : WORLD_OBJECT; |
information type about_birds
meta-descriptions birds : BIRD_ATOM; objects pos, neg : SIGN; relations has_been_discovered : BIRD_ATOM * SIGN;
|
2.3 Knowledge bases
Knowledge bases express relationships between, for example, domain specific concepts. Reasoning processes use these relationships to derive explicit additional information. Consider information type compare birds.- information type compare_birds
- information types birds;
relations same_type: BIRD * BIRD;
knowledge base birds_kbs
contents
and has_type(Z: BIRD, Y: BIRD_TYPE) then same_type(X: BIRD, Z: BIRD); if has_type(X: BIRD, type(Y: DIET, flying, Z: HABITAT)
|
|
|
|
|
3 Constraint Graphs
Constraint graphs is a concept mapping "meta-language" that allows one to visually define any number of target concept mapping languages. Once a target language is defined (for example, the DESIRE knowledge representation language) the constraint graphs program can emulate a graphical editor for the language as though it were custom build for the target language. This "custom" graphical editor can prevent the user making synactically illegal constructs and dynamically constraint user choices to those allowed by the syntax.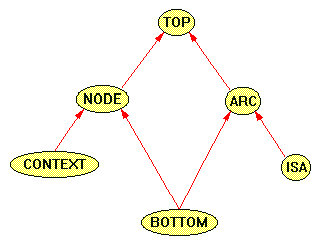 |
In order to accomodate a large number of visual languages, constraint graphs must make as few assumptions about concept mapping languages as possible. To this end, constraint graphs defines only four base components: node, arc, context, and isa (see Figure 8). Nodes and arcs are mutually exclusive, where nodes are the vertices from graph theory, and arcs interconnect other components, and are analogous to edges in graph theory. Both nodes and arcs may (or may not) be labeled, typed, and visual distinguished by color, shape, style, etc. Contexts are a subtype of node and may contain a partition of the graph. Isa arcs are a subtype of arc and are used by the system to define the subtype relation: one defines one component to the be a subtype of another component merely by drawing an isa arc from the subtype to the supertype.
Futhermore, the generality requirement of constraint
graphs dictates that arcs are not always binary, but may also be unary
or of any arbitrary arity greater than 1 (i.e., trinary and n-ary arcs
are allowed). For example, the between relation puts a trinary arc
to good use. Constraint graphs arcs may interconnect not only nodes but
other arcs as well. This is not only useful, but necessary because all
subtype and instance-of relations are defined using an isa arc,
arcs between arcs are required to define the type of any arc. Finally,
constraint graphs does not make hard distinctions between types and instances,
but rather, follows the object-delegation model (Abadi & Cardelli 1996)
where any object can function as a class or type. (Constraint graphs can
prevent a component from acting as a type using ad-hoc constraints
(Kremer 1997), but that is beyond the scope of this paper.)
 |
4. The Translator
4.1 Specifying the graphical notations in Constraint Graphs
In Constraint Graphs, three basic types of objects exist: nodes, arcs and contexts. The elements of the language to be expressed in the Constraint Graphs' environment therefore need to be mapped onto these basic types. Table 1 below shows the mapping between DESIRE's knowledge elements and nodes, arcs and contexts.|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Constraint Graphs allows the user to further constrain the language definition in Constraint Graphs by, for example, restricting the shapes and connector types of the nodes and arcs the language elements are mapped onto. In our case, we restrict the shape of node Sort to a rectangle, and the shape of Object to a diamond. Furthermore, sub-sorts, meta-descriptions and relations will be represented as directed labeled arcs, where the label takes the shape of an ellipse. Moreover, functions will be depicted as directed labeled arcs as well, but the label will be a parallelogram. Finally, information types and knowledge bases are mapped onto contexts, and the shape of these contexts will be the default: a rectangle. Although these shapes do not correspond to the shapes of the graphical representation language used in DESIRE, no confusion is expected.
Figure 10 below gives an impression of a specification of the DESIRE information type birds (compare to Figure 2) in Constraint Graphs.
 |
4.2 Implementation of the Translator
Every mature engineering discipline has handbooks to describe successful solutions for known problems. There now exists a software design patterns literature (beginning with a book by Gamma et al (Gamma, Helm, Johnson, and Vlissides, 1994)) describing successful solutions to common software problems. Industrial experience has proven that patterns are a valuable technique in software engineering problem-solving discipline. Not only do patterns capture successful experience, they also help improve communication among designers. They can help new developers avoid traps and pitfalls that traditionally can only learned by costly experience. Patterns do more than just describe solutions, they help reason deep rationale of the solutions. This section uses patterns to detail some aspects of the translator implementation.The translator was implemented with Borland C++ under Windows NT. To make the program more portable, only ANSI C++ syntax is used. The implementation details that do not relate to design patterns are omitted here.
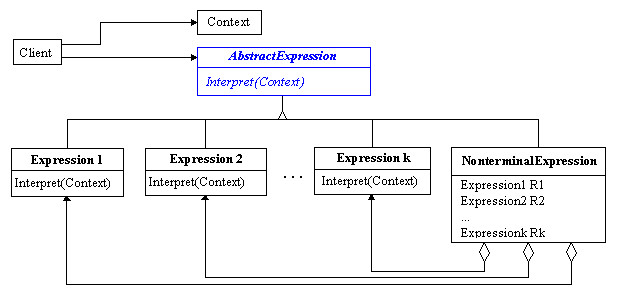
4.2.1 Interpreter Pattern
The intent of the Interpreter pattern is to represent
the grammar of a language and interpret sentences in the language (Gamma,
Helm, Johnson, and Vlissides, 1994, pp 243-255). The Interpret pattern
represents each grammar rule as a class. Symbols on the right-hand side
of grammar rule are instance variables of the class. The TerminalExpression
implements an Interpret method associated with terminal symbol in
the grammar. The NonterminalExpression implements the Interpret
method for nonterminal symbol in the grammar. Typically the Interpret
method of NonterminalExpression is implemented by calling the Interpret
methods of its subexpressions. The Interpret method takes Context
as an argument. The Context provides information global to the interpreter.
What the Context should contain totally depends on what the Interpret
method intends to do.
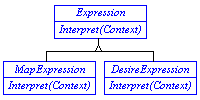 For
the translator, the class hierarchy for the Interpreter pattern has a common
abstract class Expression. Expression declares a pure virtual Interpret
method which will be inherited and implemented by all its concrete subclass.
It has two direct subclasses: MapExpression and DesireExpression.
These two classes are also abstract classes. They act as the base classes
of Constraint Graph and DESIRE object hierarchies respectively. All Constraint
Graph expression nodes are subclasses of MapExpression; all DESIRE
expression nodes are subclasses of DesireExpression.
For
the translator, the class hierarchy for the Interpreter pattern has a common
abstract class Expression. Expression declares a pure virtual Interpret
method which will be inherited and implemented by all its concrete subclass.
It has two direct subclasses: MapExpression and DesireExpression.
These two classes are also abstract classes. They act as the base classes
of Constraint Graph and DESIRE object hierarchies respectively. All Constraint
Graph expression nodes are subclasses of MapExpression; all DESIRE
expression nodes are subclasses of DesireExpression.
Terminal Expression
For TerminalExpression, the implementation of the representing class is simple and straightforward. Besides the attributes and methods needed for normal functioning, it must implement the virtual Interpret method inherited from base class. The Interpret method will interpret the corresponding terminal symbol that the class represents. For example, DESIRE has a grammar rule defining variables:
<variable> ::= <variable_name> ":" <sort_name>This is a terminal expression. This grammar rule was modeled as class DesireVariable shown in Listing 2.
class DesireVariable : public DesireExpression {
public:
...
int Interpret(Context);
...
protected:
String varName;
String sortName;
};
|
int DesireVariable::Interpret(Context c)
{
if(c.defined(sortName) && c.typeOf(sortName) == "sorts")
return 1;
else
return 0;
}
|
Nonterminal Expression
For NonterminalExperssion, as described in Gamma, et al:
- "one such class is required for each rule R::=R1R2...Rn in the grammar".
- "maintains an instance variable of type AbstractExpression for each of the symbols R1 through Rn in the grammar".
- "implements an Interpret operation for nonterminal symbols in the grammar. Interpret typically calls itself recursively on the variables representing R1 through Rn" (Gamma, Helm, Johnson, and Vlissides, 1994, p. 246).
Note the use of the word type, instead of class before AbstractExpression. This should be taken to imply that the instance variable is some subtype of AbstractExpression, not precisely AbstractExpression. In class-based languages (e.g., C++), subclassing is subtyping (Abadi and Cardelli, 1996). By subsumption, a value of type A can be viewed as a value of a supertype B. So, if c' is a subclass of c, then an instance of class c' is an instance of class c. A subtype can be used in any place where a supertype can be used. Since any subclass type is of its base class type, the instance variables type can be the type of any subclasses of AbstractExpression.
For example, consider the following grammar rule of DESIRE.
knowledge_base::= knowledge base <kb_name> [knowledge_base_interface] [knowledge_base_reference] knowledge_base_contents end knowledge base. |
class DesireKB : public DesireExpression {
public:
...
Interpret(Context);
...
protected:
string name;
DesireKBInterface* kbInterface;
DesireKBReference* kbReference;
DesireKBContent kbContent;
};
|
- The static object types of symbols in NonterminalExpression are made obvious. It is easier to relate classes to grammar rules.
- It is more type-safe. Since the type of instance variables are all specific subclasses type, not the generic AbstractExpression, there are no need to get the instance types at run time. While using these instance variables, there are no need to use dynamic_cast<> to get their actual types dynamically.
- Statically specifying instance variable's type can also ensure objects of the wrong type cannot be set/added to the NonterminalExpression. Therefore, the instance of NonterminalExpression will not contain wrong types of instance variables. The creation of NonterminalExpressions will be less error-prone.
int DesireKB::Interpret(Context c)
{
int ret = 1;
if(kbInterface)
ret = ret && kbInterface->Interpret(c);
if(kbReference)
ret = ret && kbReference->Interpret(c);
ret = ret && kbContent.Interpret(c);
return ret;
}
|
The class structure of the implementation is shown in Figure 11.
 |
Context
Context provides information that is global to the Interpreter. The kind of attributes and methods that class Context should have depend on what kind of operation the Interpret method intends to do. One Interpret method of Constraint Graph is to draw the graphics. So the Context class provides the device handle of the drawing, and the drawing position, as shown in Listing 7.
class Context {
public:
Context();
virtual ~Context();
void SetPoint1(TPoint&);
void SetPoint2(TPoint&);
void SetDevice(DEVICE);
TPoint GetPoint1();
TPoint GetPoint2();
DEVICE GetDevice();
protected:
TPoint p1;
TPoint p2;
DEVICE Device;
};
|
The Interpreter pattern distributes the Interpret method over the whole class structure. Every class in the class structure needs to be modified if another kind of interpretation is needed, i.e., new Interpret methods must be added into each class. When there are many classes in the class structure, it will be very time-consuming and error-prone to make such changes.
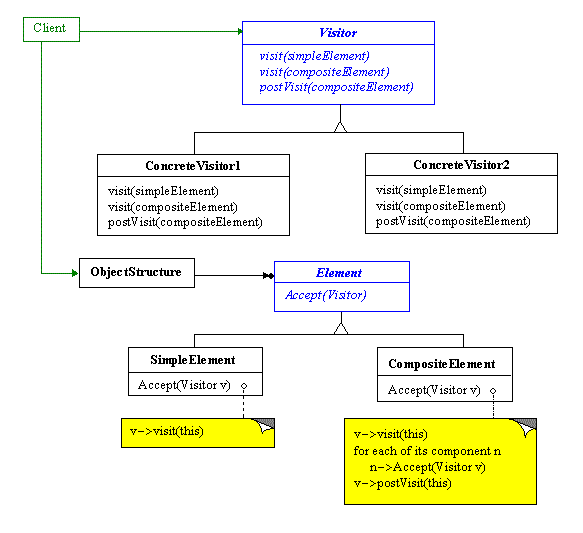
The Visitor pattern represents an operation to be performed on the elements of a class structure (Gamma, Helm, Johnson, and Vlissides, 1994, pp 331-344). Each Visitor is a set of related operations that can be performed on the elements of the class structure. New operations can be introduced without changing the classes of the elements on which it operates. The Visitor pattern deals with two class hierarchies: the Visitor, and the Elements on which the Visitor operates. For each concrete class in the Element class hierarchy, a visit method is defined in the Visitor class. Each class of the Element hierarchy defines an Accept method which introduces Visitor into the class hierarchy. Element class sends a request to Visitor by calling the Accept method which takes an object of the Visitor class as its argument. The Accept method invokes the visit method defined in the Visitor class and passes the object itself as the argument to the visit method.
The Elements of current system are the class hierarchy of the Interpreter pattern implementations. The subsection below describes the implementation of the Visitor.
Visitor
An abstract Visitor class is defined so that more than one operation can be defined. Each kind of operation can be defined as a concrete subclass of the abstract Visitor class. In the abstract Visitor class, a pure virtual method visit is defined for each TerminalExpression class; however, for NonterminalExpression, two visit methods, visit and postVisit, are defined. The visit method visits the element before visiting its composing components. The postVisit method visits the element after visiting its composing components.
The reason for defining two visit methods for NonterminalExpression is due to its inherent structure. NonterminalExpression is composed of other expressions. No presumption can be made about when Visitor should "visit" its composing components, either before or after visiting itself. In addition, such nodes may need some pre-processing before they process their constituent components, and some post-processing after they have processed their constituent components. Defining two visit methods for NonterminalExpression classes solves both problems.
Element
Each element defines an Accept method
which takes Visitor as an argument. By calling Accept, the
element sends a request to Visitor, and passes itself as the argument.
The Visitor will then perform the desired operation for the element.
Listing 8 shows the Accept method of DesireVariable class.
As mentioned above, no presumptions can be made about when its composing components should be visited for NonterminalExpression, the Accept method of such nodes must send requests to Visitor twice: one before visiting its composing components, the Visit function call, and again after visiting its composing components, the postVisit function call, as shown in Listing 9.
Sample Code
Below is some code segments of the pretty printing visitor pattern used in the translator.
void DesireVariable::Accept(DesireVisitor& v)
{
v.Visit(this);
}
void DPrettyPrintVisitor::visit(DesireVariable* v)
{
if(needComma) out << ',';
else needComma = 1;
out << v->GetName() << ":" << v->GetSort();
currentCol += (v->GetName().length() + v->GetSort().length() + 1);
needComma = 1;
}
|
void DesireKB::Accept(DesireVisitor& v)
{
v.Visit(this);
if(kbInterface)
kbInterface->Accept(v);
if(kbReference)
kbReference->Accept(v);
kbContent.Accept(v);
v.postVisit(this);
}
void DPrettyPrintVisitor::visit(DesireKB* kb)
{
if(currentCol)
out << endl;
numberOfTabs = 1;
out << "knowledge base " << kb->GetName() << endl;
currentCol = 0;
}
void DPrettyPrintVisitor::postVisit(DesireKB*)
{
if(currentCol)
out << endl;
out << "end knowledge base." << endl << endl;
numberOfTabs = 0;
currentCol = 0;
}
|
Class Structure
The class structure of the implemented Visitor pattern is shown in Figure 12.
 |
5. Relation to Conceptual Graphs
In this paper, graphical notations for knowledge in DESIRE are presented, as well as a translator which translates specifications of these notations in a graphical environment called Constraint Graphs to the original textual DESIRE language. Having this graphical interface brings the knowledge modelling in DESIRE closer to other well-known knowledge representation languages, such as Conceptual Graphs (Sowa, 1984). A conceptual graph is a finite, connected, bipartite graph, which consists of two kinds of nodes: concepts and conceptual relations (Sowa, 1984, p. 73). Concepts are denoted by a rectangle, with the name of the concept within this rectangle, and a conceptual relation is represented as an ellipse, with one or more arcs, each of which must be linked to some concept. Figure 13 below shows an example conceptual graph, representing the episodic knowledge that a girl, Sue, is eating pie fast.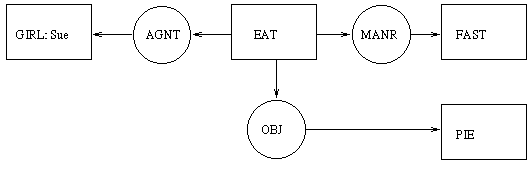 |
Sorts: Sorts conform to generic concepts in Conceptual Graphs. The notations are the same.
Objects: Objects are instances of a sort in the real world. Sowa (1984, p. 85) denotes these instances with individual concepts, concepts with an individual marker following the concept name: [BIRD: tweety]. This notation is short for the following: [BIRD]->(NAME)->["tweety"]. The objects-diamond in DESIRE can be mapped to an individual marker in Conceptual Graphs, and the instance_of arrow in the graphical notation can be compared to the conceptual relation NAME. In the case of an anonymous individual, the graphical DESIRE notation is comparable to the notation in Conceptual Graphs: if one knows that an individual of type BIRD exists, but it is unknown which individual, then this information is represented as [BIRD: *x].
Functions: In DESIRE, functions group sorts together by mapping them onto another sort. Functions can be regarded to be subtypes of a general concept FUNCTION, which takes one or more arguments and produces a result. Function SQRT, for example, can be defined as follows (Sowa, 1984, p. 415):
[NUMBER]<-(ARG)<-[SQRT]->(RSLT)->[NUMBER]In this graph, SQRT is a subtype of FUNCTION, taking one argument of type NUMBER and producing a result of type NUMBER. In DESIRE, functions do not calculate a number based on another number or other numbers, but functions act as a named placeholder for an object of its result, in which the argument(s) and the name of the function ensure the placeholder's uniqueness. Function mileage_function, for example, maps a car to a number and could be represented as the following Conceptual Graph:
[CAR]<-(ARG)<-[MILEAGE_FUNCTION]->(RSLT)->[NUMBER].This function can be used in constructions such as smaller(mileage(R: RENAULT), 30), stating that the mileage of a Renault is smaller than 30.
Relations: Relations can be classified according to their arity. This arity determines the mapping to Conceptual Graphs. 0-ary relations in DESIRE will have to be translated to concepts; concepts in Conceptual Graphs form a graph in itself, like relations form a DESIRE atom in DESIRE. Relations with an arity greater than zero can be translated into either a conceptual relation with the same arity or a combination of a concept and (an)other conceptual relation(s). For example, the relation between: space * brick * brick in DESIRE could be translated into the following Conceptual Graph:
[SPACE]->(BETW)->[BRICK] ->[BRICK]This graph is a triadic relation, which could be read as "a space is between a brick and a brick". Relation travel: person * origin * destination however should be translated into the graph
[TRAVEL] - (AGNT)->[PERSON] (ORG)->[ORIGIN] (DEST)->[DESTINATION]In Conceptual Graphs, TRAVEL is regarded to be a concept and not a conceptual relation. This is why relation travel in DESIRE is translated into a concept TRAVEL, connected to person, origin and destination by conceptual relations that specify the role these concepts play in the TRAVEL-graph.
Sub-sorts: Sub-sorts in DESIRE correspond to the type hierarchy of concepts in Conceptual Graphs. In Conceptual Graphs, hierarchies of both concepts and conceptual relations are possible, but these hierarchical is-a relations are kept in a separate semantic net from other relations that exist in the domain. In DESIRE, hierarchical relations between sorts are allowed; the sub-sort-relation is one of the many relations that may exist between sorts in a domain.
Information types, knowledge bases, antecedents, consequents and not-boxes: DESIRE's information types, knowledge bases, antecedents, consequents and not-contexts can be regarded as contexts in Conceptual Graphs. Although the graphical DESIRE notation uses a different icons to represent these contexts, these contexts can be represented by labelled rectangles in Conceptual Graphs, where the labels of these rectangles denote the type of the context (information type, knowledge base, antecedents, consequents, and not-boxes).
Information type and knowledge base references: In DESIRE, mechanisms exist to enable compositionality of information types and knowledge bases: information type- and knowledge base references, see Figures 3 and 6. In Conceptual Graphs, contexts that contain other contexts represent this contain-relation by enclosing context-boxes in other context-boxes. Therefore, the graphical DESIRE notations for this compositionality can be translated to Conceptual Graphs notation by placing information types in information types and knowledge bases in knowledge bases.
Meta-descriptions: Another, different relation exists between information types: the meta-description. A information type A in DESIRE is said to contain a meta-description of a information type B if information type A can be used to specify as terms the atoms that can be specified using the vocabulary of information type B. This means that information type A allows for expressing statements that are at a meta-level with respect to the language defined in information type B. The meta-description relationship is expressed in the graphical notation as a connection, between the meta-described information type B to a sort in the meta-level information type A. This object-meta-level relation between information types is very specific to DESIRE. In Conceptual Graphs, this relationship between information types A and B could be expressed as the conceptual relation [Information type B]->(METALEVEL)->[Information type A], with the intended meaning that information type A is at a meta-level with respect to information type B.
Knowledge base to information type reference: The graphical DESIRE notation for a knowledge base referencing an information type is a connection from the knowledge base to that information type. This connection indicates that the knowledge base, which contains facts and rules that hold in the application domain, uses that information type as the vocabulary to express those facts and rules. One could argue that a information type can be compared to the first three parts of a cannon (Sowa, 1984, p.96), which is a set of four components used to derive canonical graphs: a type hierarchy (sorts and sub-sorts), a set of individual markers (objects), a conformity relation (the sorts the objects belong to) and a finite set of conceptual graphs (the graphs that are true in the domain). The knowledge expressed in knowledge bases would then conform to the fourth component of the canon: the set of graphs that are true in the domain.
The implies arrow: The last candidate for comparison is the labeled arrow "implies", which connects the antecedent and consequent of a rule in the graphical DESIRE notation. This arrow can be translated into a relation 'IMP', a logical operator denoting the implication between propositions (Sowa, p. 147). 'IMP' is defined as follows:
- relation IMP(x,y) is [*x] [*y]
(NEG)->[ [*x] (NEG)->[ [*y]]].
This concludes the brief comparison of the graphical
DESIRE notations to Conceptual Graphs. Table 2 below summarizes the mapping
sketched above.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6. Conclusion
In this paper, graphical representations for knowledge structures in DESIRE (Brazier Dunin-Keplicz, Jennings & Treur 1995; Brazier, Treur, Wijngaards & Willems 1996) have been presented, together with a graphical editor based on the Constraint Graph environment (Kremer 1997). Moreover, a translator has been described which translates these graphical representations to textual representations in DESIRE. This software environment can be regarded as a graphical design tool for knowledge in DESIRE, an interface which offers many advantages to a textual interface. First, Constraint Graphs can be used to specify knowledge structures, allowing the user to work with a mouse, pull-down menu's and windows instead of typing the specification conform the textual DESIRE syntax. Second, Constraint Graphs offers a clear visual representation, facilitating communication between domain expert and knowledge engineer in the development process. Third, the graphical representations bring DESIRE closer to other knowledge representation languages, such as Conceptual Graphs (Sowa, 1984). In conclusion, the strengths of the Constraint Graphs environment as an easy to use representation tool in combination with the DESIRE environment allows for a powerful framework to support the development of knowledge based or multi-agent systems.References
Abadi, M. and Cardelli, L. (1996). A Theory of Object, Springer, New York, 1996Brazier, F.M.T., Dunin-Keplicz, B., Jennings, N.R. and Treur, J. (1995). Formal specification of Multi-Agent Systems: a real-world case. In: V. Lesser (Ed.), Proceedings of the First International Conference on Multi-Agent Systems, ICMAS-95, MIT Press, Cambridge, MA, pp. 25-32. Extended version in: International Journal of Cooperative Information Systems, M. Huhns, M. Singh, (Eds.), special issue on Formal Methods in Cooperative Information Systems: Multi-Agent Systems, vol. 6, 1997, pp. 67-94.
Brazier, F.M.T., Treur, J., Wijngaards, N.J.E., Willems, M. (1996) Temporal Semantics of Complex Reasoning Tasks, In: B. Gaines, M. Musen (eds.), Proceedings of the 10th Knowledge Acquisition Workshop, KAW'96, Banff, University of Calgary, pp. 15/1-15/17. Extended version to appear in Data and Knowledge Engineering
Gamma, E., Helm, R., Johnson, R., and Vlissides,
J. (1994). Design Patterns: Elements of Reusable Object-Oriented Software,
Addison-Wesley, Reading, Mass., 1994
Kremer, R. (1997). Constraint Graphs: A Constraint
Graphs Meta-Language, PhD Dissertation, Department of Computer Science,
University of Calgary, 1997
Moeller J.U., Willems M. (1995). CG-DESIRE:
Formal Specification Using Conceptual Graphs; Gaines, B.R. and Musen,
M.A. (eds), Proc. of the 9th Banff Knowledge Acquisition for Knwoledge-Based
Systems Workshop KAW-95, Calgary, pp. 25/1 - 25/20.
Nosek, J. T. & Roth, I. 1990. A Comparison of Formal Knowledge Representation Schemes as Communication Tools: Predicate Logic vs. Semantic Network, International Journal of Man-Machine Studies, 33: 227-239, 1990.
Sowa, J.F. (1984). Conceptual Structures: Information
Processing in Mind and Machine, Addison-Wesley, Reading, Mass., 1984.