Visual languages of many types are used in many disciplines for many purposes. The use of visual languages is compelling for many reasons, not the least of which is that their graphical nature can act as an analogical representation of the actual domain in a way that is not possible with purely textual systems. Concept mapping languages form a large family of visual languages. Concept maps consist of labeled, typed nodes and typed arcs, and may also include contexts that partition the map. Concept maps appear to be particularly useful for knowledge representation; examples include Peirce's Existential Graphs, Sowa's Conceptual Graphs, and Gaines' KRS.
This paper focuses on visual languages; in particular, the field is narrowed (slightly) by concentrating on concept map-based visual languages. Here, a concept map consists of nodes and arcs and possibly other constructs, such as contexts. Thus, visual languages based on matrices (spreadsheets), forms (query by example), purely spatial relationships (iconic sentences), and simple text layout (outlining tools) are eliminated. All of the example languages used in this paper either fall into the category of concept maps, or have concept map languages which implement them. For example, Conceptual Graphs has both a graphical form (concept map) and a "linear form" (textual); and Gaines (1991b) has developed a visual language for CLASSIC, called KRS (Knowledge Representation System).
Although the focus of this paper is on formal and semi-formal visual knowledge representation, informal representations are not completely neglected, for they are often useful (Kremer 1994; 1995):
void makeupper(char* buf)
{
char* i;
for (i=buf; *i; i++)
{
*i = toupper(*i);
}
}
In spite of the visual aids, this is still considered a textual language.
Visual languages all involve pictures of some sort - whether as simple
as nodes and connecting arcs, or as complex as nested, multi-dimensional
sentences of iconic pictures. Of course, visual languages often involve
text, but text's role is usually limited to labels or brief explanations
or annotations.
It can be argued that not all people are good at reading graphical representations of data and knowledge. The point seems obvious, but Petre and Green have found evidence that "seeing" the information in a graphical display is an acquired skill (Petre & Green 1993). In contrast to Nosek and Roth's study, Petre and Green's study found that subjects could solve problems faster with their textual languages than with their graphical languages; however, they conclude that although people seem to have to work harder to read graphical information, the graphical notations may prove much richer for expert users. Indeed, there is still not sufficient evidence to evaluate the usefulness of visual languages. Myers (1990) notes the lack of evidence:
"There are not many Visual Languages that would be generally agreed are 'successful', and there is little in the way of formal experiments or informal experience that shows that Visual Languages are good. It would be interesting to see experimental results that demonstrated that visual programming techniques or iconic languages were better than good textual methods for performing the same tasks. Metrics might include learning time, execution speed, retention, etc. Fortunately, preliminary results are appearing for the advantages of using graphics for teaching students how to program." (p. 117)Regardless of the lack of firm evidence, there is much intuitive appeal to graphical languages. Smith (1977) describes the psychological motivations for using visual languages for programs and data. Among Smith's many arguments are:
"The standard notation for symbolic logic was developed by mathematicians like Peano, Russell, and Whitehead, who patterned it after algebra. But one of the pioneers of logic, Charles Sanders Peirce, switched to a graph notation after making major contributions to the linear form. His existential graphs, which he called 'the logic of the future,' form the logical basis for conceptual graphs." (p. 138)While Peirce's graphical notations (visual logic languages) have not been well-accepted by mainstream logicians, his invention and use of them argue for their utility for this "pioneer of logic". Peirce himself writes:
"I do not think I ever reflect in words: I employ visual diagrams, firstly because this way of thinking is my natural language of self-communion, and secondly, because I am convinced that it is the best system for the purpose [Ms 620, p. 8]" (Roberts 1973, p. 126)Roberts (1973), in his book about Pierce's existential graphs, argues for the usefulness of the visual logic language:
"Logic diagrams these days are certainly less familiar than algebraic notations of logic. But are they really too cumbersome? Would it be fair to say that they are "less perspicuous than the usual" notations, as some say of the Polish notation (Church 1956)? Well, if a facile and perspicuous notation is one that can be quickly learned and easily manipulated, then years of experience with university students have convinced me that EG is the most perspicuous, and Principia notation the least. The unusual ease with which inferences can be drawn in EG is something of an unexpected bonus." (p. 126)The current popularity of direct manipulation interfaces (Shneiderman 1986) is completely compatible with visual languages since many are subject to manipulation with a mouse or other pointing device.
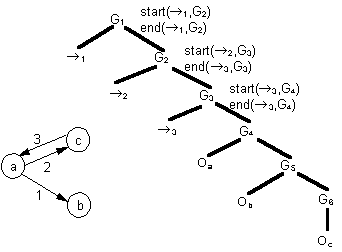
Crimi et al (1991) describe the application of relational grammars to multi-dimensional (visual) languages in order to define a visual syntax. In their formulation, a context-free relational grammar is a tuple,
VN = {G}
VT = {O,->}
VR = {start,end}
P = 1. G::={O}
2. G::={O,G}
3. G::={->,G} {start(->,G), end(->,G)}
R = 1. start(->,G) :- (G => {O}), start(->,O)
2. start(->,G1) :- (G1 => {O,G2}), start(->,O)
3. start(->,G1) :- (G1 => {O,G2}), start(->,G2)
4. start(->1,G1) :- (G1 => {->2,G2}), start(->1,G2)
5. end(->,G) :- (G => {O}), end(->,O)
6. end(->,G1) :- (G1 => {O,G2}), end(->,O)
7. end(->,G1) :- (G1 => {O,G2}), end(->,G2)
8. end(->1,G1) :- (G1 => {->2,G2}), end(->1,G2)
Production 1 says that a single node is a legal graph. Production 2 says
a single node can always be added to a graph. Production 3 says a directed
arc can only be added to a graph if it starts and ends in the graph.
The evaluation rules, R, specify how the start and end relations are to be interpreted. They are defined recursively in a Prolog-like language. For example, Rule 1 states that a directed arc starts on G if G matches a single node (G => {O}), and the arc starts on that node (start(->,O)). Rules 2 and 3 state that a directed arc starts on G1 if G1 matches {O,G2} and the arc starts on the node (start(->,O)) or on a node in G2 (start(->,G2)). Figure 1 shows a simple directed graph and its parse tree according to this relational grammar.

In contrast, Wang and Lee (1993) do not concern
themselves with syntax, but go a step in the direction of semantics. They
describe a formal semantics for visual reasoning. In their formulation,
graphs are given meaning by an interpretation that maps the graphical
domain to an application domain:
A graphical signature, S, is a quadruple (T, <, F, P) where:
| Textual languages | |
| Concept maps | Flowcharts |
| Flowchart derivatives | |
| Petri nets | |
| Data flow graphs | |
| Directed graphs | |
| Graph derivatives | |
| Matrices | |
| Jigsaw puzzle pieces | |
| Forms | |
| Iconic sentences | |
| Spreadsheets | |
| Demonstrational | |
| None |
There are other taxonomies of visual languages, but Myers' are the most well-known, and the others tend to specialize within a specific area. For example, Price, Baecker and Small quantitatively grade their 12 example program visualization languages in each of over 30 leaf-node categories arranged in a four level hierarchy (Price, Baecker & Small 1993).
Concept maps are graphs (in the mathematical sense of the word) consisting of nodes with connecting arcs, which represent relationships between nodes (Lambiotte et al. 1984). The nodes are labeled with descriptive text, representing the "concept", and the arcs are often labeled with a relationship type. Nodes may be represented using distinct visual attributes, such as shape and color, to distinguish node types; arcs may be similarly distinguished. Thus, concept maps model a simple graph theory. The notion of concept map may be extended to include contexts, boxes that contain a subgraph (sub-concept map) of the graph (concept map), which models partitions in graph theory.
Figure 2 is an example of an informal
concept map developed by a group during an interactive brainstorming session
about a new network in a large company. In contrast, Figure
4 shows a formal concept map, called a Conceptual Graph (Sowa
1984), which models the sentence "Tom believes Mary wants to marry
a sailor" in a way that is amenable to straightforward, unambiguous interpretation
by a computer program.
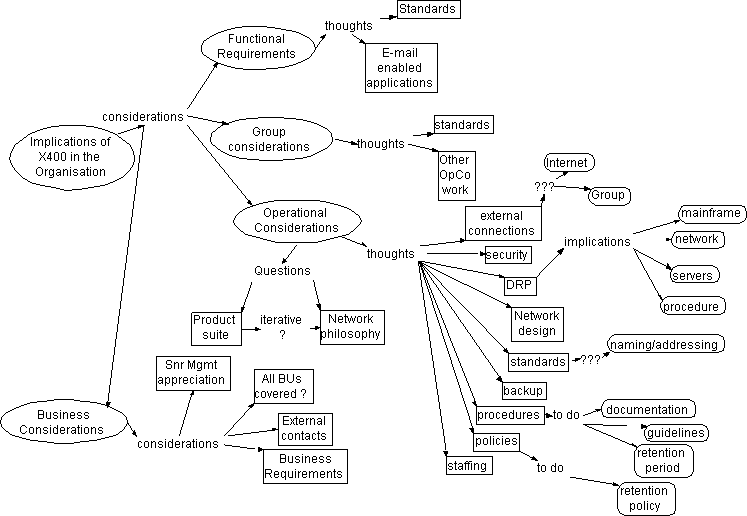
Table 2 shows where concept maps fit into Myers' taxonomy of visual languages, subsuming six of his 14 categories and constituting 24 of his 39 example visual languages. Any of the various forms of concept maps may be described in terms of Crimi et al's relational grammars (Crimi et al. 1991) in a manner very similar to the example given in Section 1.2. This example, however, only considers directed graphs, while concept maps may contain directed, undirected, and bi-directional arcs -- or a mix of these. The example is also overly simple in that it assumes only untyped nodes and arcs, while concept mapping languages usually include typed nodes and/or typed arcs where the rules include constraints on the interconnections based on type.
In terms of Wang and Lee's semantics (Wang & Lee 1993), the term concept map is too general to be assigned a mapping to a specific application domain: there are many concept mapping languages which each map to their own set of application domains. However, one can describe the graphical signature, S, of concept maps at a high level (top and null are the universal type and the absurd type, respectively):
| S: | T | top, pos_int, graph, node, arc, null |
| < | graph < top, node < graph, arc < graph, null < node, null < arc, pos_int < top, null < pos_int | |
| F | anchored_to: arc x pos_int -> node | |
| P | anchored: arc x pos_int x node |
Lambiottte, Dansereau, Cross, and Reynolds (1984) classify "multirelational semantic maps" into four categories:
The remainder of this paper focuses on examples of concept mapping languages. These include two languages for knowledge representation and one language for decision making.
In order to illustrate visual knowledge representation languages, this section describes two very different visual knowledge representation languages: Gaines' KRS, a visual form of CLASSIC; and Sowa's Conceptual Graphs, which has both a graphical and linear (textual) form.
define-role[perpetrator] define-role[victim] ... define-concept[CRIME, (PRIMITIVE (AND (AT-LEAST 1 perpetrator) (ALL perpetrator PERSON) (AT-LEAST 1 victim) (AT-LEAST 1 site) (AT-MOST 1 site)) crime)].CLASSIC works by classifying individuals as members of one or more concepts in a concept hierarchy. Information about concepts and individuals is encoded as roles (attributes or slots) and associated values. CLASSIC matches the roles and values of individuals to infer which concepts an individual belongs to. Once an individual has been classified, rules associated with the concepts may be fired to further instantiate knowledge about the individual (by filling in roles and role values).
There has been extensive work on complexity of the subsumption algorithms in KL-ONE languages (Donini et al. 1995). The subsumption algorithm is important because subsumption calculation is the basis of all computation in KL-ONE languages. It turns out that extension of a base level version of KL-ONE (composed of conjunction, limited negation, universal quantification, limited role existential quantification, and numeric role filler limits) leads to worst-case complexities of NP-hard or worse. Fortunately, subsumption seems to be computationally tractable in practical situations.
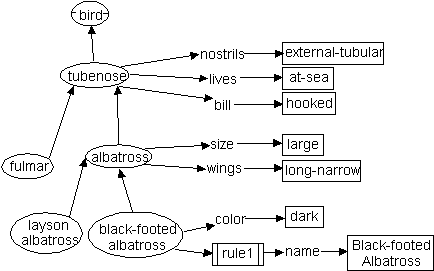
Gaines has developed a visual version of the CLASSIC language, called KRS in which the user can specify and run a complete expert system (Gaines 1991b). A small excerpt from a knowledge base about birds is illustrated in Figure 3. The ellipse with tick marks identifies bird as a primitive concept. The unmarked ellipses labeled tubnose, albatross, fulmar, layson albatross, and black-footed albatross represent subconcepts of bird as shown by the directed arcs. The labels with no surround are roles and the labels with rectangular surrounds are individuals which, in this case, are acting as values for the roles. The interpretation is that an observed individual of type bird may be recognized as a tubenose if it is observed that its nostrils are external-tubular, it lives at sea, and its bill is hooked. The class of the bird may be further refined by further observation as pictured. If a bird is classed as the concept black-footed albatross, then a rule is fired (rule1 in the barred rectangle) which assigns "Black-footed Albatross" to its name role. A complete KRS knowledge base would have information about many other birds, descriptions of the types of things that can play the value part for each role, and various other pieces of information such as the mutual exclusion among certain concepts.
Conceptual graphs are capable of cleanly representing an extremely wide range of knowledge forms - from predicate logic to natural language. For example, Figure 4 is a conceptual graph representation of the surprisingly complex sentence "Tom believes that Mary wants to marry a sailor." Conceptual graphs are bipartite, with rectangular boxes representing concepts (and individuals) and rounded (or elliptical) boxes representing relations between the concepts (and individuals). The larger boxes in Figure 4 are also concepts but are a special kind of concept called contexts. The outer concepts may be read as "There is an instance of a belief whose experiencer is the person Tom, and whose patient is a certain proposition." The proposition is "There is an instance of a want whose experiencer is a person Mary and whose patient is a certain situation." The situation is "There is an instance of marriage whose agent is something (T) and whose patient is some sailor." There is also a coreference link (the dotted line) between the concept [Person: Mary] and the concept [T]. This indicates that [Person: Mary] and [T] are the same individual, which modifies the interpretation of the situation to be "There is an instance of marriage whose agent is a person Mary and whose patient is some sailor."
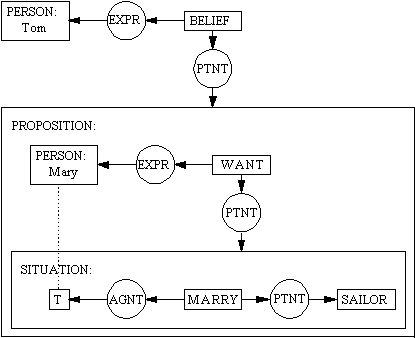
The linear form of the conceptual graph in Figure 4 is
[BELIEF] - (EXPR) -> [PERSON:Tom] (PTNT) -> [PROPOSITION: [WANT] - (EXPR) -> [PERSON:Mary] (PTNT) -> [SITUATION: [MARRY] - (AGNT) -> [T:Mary] (PTNT) -> [SAILOR] ] ]which represents the boxes (concepts) in Figure 4 with square brackets and the circles (relations) with round parenthesis. The arcs have fairly obvious translations using "->" and "<-". The one element that does not translate in a straightforward "graphical" manner is the coreference arc (dotted arc); coreference is represented only implicitly by the coincidence of the variable name Mary.
The above example serves to show that Conceptual Graphs can represent natural language sentences, but Sowa (1984) shows how Conceptual Graphs can be used to interpret natural language and to generate natural language as well. Furthermore, Conceptual Graphs are shown to represent first order logic (with an elegant set of visual deduction rules) and model logic.
The description of Conceptual Graphs given so far involves only the graphs themselves. A complete Conceptual Graphs definition is a canon consisting of the graphs, a type lattice (semantic net), the conformity relations (instance-of relations), and the formation rules. The graphs have already been discussed. The type lattice is a semantic net describing the subtype/supertype relationships among the concept and relation types used in the graphs. The conformity relations list describe the types of all individuals used in the graphs, so are ordered pairs from individuals to the elements in the type lattice. Finally, the formation rules are:
There now exist several tools for the storage and manipulation of Conceptual Graphs. These include PEIRCE (Ellis & Levinson 1992), Deakin ToolSet (Lukose 1991), and CGKEE (Munday et al. 1996). These tools are all based on the Conceptual Graphs linear form.
In addition, there have been several extensions to Conceptual Graphs. Lukose has developed Model-ECS (Lukose 1993; Lukose 1995) which is an executable form of Conceptual Graphs.
The syntax and semantics of visual languages is as varied as visual languages themselves, but Crimi et al (1991) have applied relational grammars to visual languages to formalize their syntax. Furthermore, Wang and Lee (1993) have addressed the semantics of visual languages by formalizing a system to describe an interpretation from the graphical (visual) domain to an application domain.
There exist several taxonomies of visual languages; however, Myers (1990) is the most well known and most inclusive. Myers uses three separate taxonomies to classify languages as programming systems, by specification technique, and by what artifacts they represent.
Concept maps are a general kind of visual language and are used for many purposes. Concept maps are graphs with nodes, arcs that interconnect the nodes, and possibly contexts which partition the map. Concept maps may be described in terms of Crimi et al's relational grammar and in terms of Wang and Lee's semantic interpretations, but concept map is too general a term to describe specific interpretations: interpretations must be applied to specific applications of concept maps.
Two specific concept mapping languages used in knowledge representation and reasoning are described. Gaines' KRS is an visual version of the CLASSIC knowledge representation language used in artificial intelligence applications. Sowa's Conceptual Graphs is also a knowledge representation language, and is used in natural language interpretation, natural language generation, and reasoning.
Axelrod, R. 1976. Structure of Decision. Princeton, New Jersey, Princeton University Press.
Banathy, B. H. 1991. Cognitive mapping of educational systems for future generations. World Future 30(1): 5-17.
Borgida, A., Brachman, R. J., McGuiness, D. L. & Resnick, L. A. 1989. CLASSIC: A Structural Data Model for Objects. Proceeding of 1989 SIGMOD Conference on the Management of Data. New York, ACM Press: 58-67.
Brazier, F., Dunin-Kepliczb, B., Treura, J., Verbruggea, R.. 1996. Beliefs, Intentions and DESIRE. KAW'96: Tenth Workshop on Knowledge Acquisition, Modeling and Management, Gaines, B., Musen, M. (eds.), Voyager Inn, Banff, Alberta, Canada, November 8-14, 1996. http://ksi.cpsc.ucalgary.ca/KAW/KAW96/brazier/default.html.
Calcinelli, D. & Mainguenaud, M. 1994. Cigales, a Visual Query Language for a Geographical Information System: the User Interface. Journal of Visual Languages and Computing 5(2): 113-132.
Church, A. 1956. Introduction to Mathematical Logic. Princeton, N. J., Princeton University Press.
Conklin, J. & Begeman, M. L. 1987. gIBIS: A Hypertext tool for Team Design Deliberation. Hypertext'87: 247-251.
Constabile, M. F. & Catarci, T., Eds. 1995. Special Issue on Visual Query Systems. Journal of Visual Languages and Computing 6(1).
Crimi, C., Guercio, A., Nota, G., Pacini, G., Tortora, G. & Tuccit, M. 1991. Relation Grammars and their Application to Multi-dimensional Languages. Journal of Visual Languages and Computing 2(4): 333-346.
Cuena, J. & Molina, M. 1996. Building Knowledge Models Using KSM. KAW'96: Tenth Workshop on Knowledge Acquisition, Modeling and Management, Gaines, B., Musen, M. (eds.), Voyager Inn, Banff, Alberta, Canada, November 8-14, 1996. http://ksi.cpsc.ucalgary.ca/KAW/KAW96/molina/kaw_demo.html.
Donini, F., Lenzerini, M., Nardi, D. & Nutt, W. 1995. The Complexity of Concept Languages, Deutsches Forschungszentrum fur Kunstleche Intelligenz GmbH.
Eden, C., Jones, S. & Sims, D. 1979. Thinking in Organizations. London, Macmillan.
Eklund, P. W., Leane, J. & Nowak, C. 1993. GRIT: Toward a Standard GUI for Conceptual Structures. Second International Workshop on PEIRCE: A Conceptual Graphs Workbench. Laval University, Quebec, Canada.
Ellis, G. & Levinson, R., Eds. 1992. Proceedings of the First International Workshop on PEIRCE: A Conceptual Graphs Workbench. Las Cruccs, New Mexico.
Euzenat, J. 1996. HyTropes: A WWW Front-end to an Object Knowledge Management System. KAW'96: Tenth Workshop on Knowledge Acquisition, Modeling and Management, Gaines, B., Musen, M. (eds.), Voyager Inn, Banff, Alberta, Canada, November 8-14, 1996. http://ksi.cpsc.ucalgary.ca/KAW/KAW96/euzenat/euzenat96c.html.
Gaines, B. R. 1991a. Empirical Investigation of Knowledge Representation Servers: Design Issues and Applications Experience with KRS. AAAI Spring Symposium on Implementing Knowledge Representation and Reasoning Systems. Stanford, CA.
Gaines, B. R. 1991b. An Interactive Visual Language for Term Subsumption Languages. IJCAI-91. Sydney, Australia.
Gaines, B., Norrie, D., Lapsley, A. & Shaw, M. 1996. Knowledge Management for Distributed Enterprises. KAW'96: Tenth Workshop on Knowledge Acquisition, Modeling and Management, Gaines, B., Musen, M. (eds.), Voyager Inn, Banff, Alberta, Canada, November 8-14, 1996. http://ksi.cpsc.ucalgary.ca/KAW/KAW96/gaines/KMDE.html.
Graesser, A. C. & Clark, L. F. 1985. Structures and Procedures of Implicit Knowledge. New Jersey, Ablex.
Hart, J. A. 1977. Cognitive Maps of Three Latin American Policy Makers. World Politics 30(1): 115-140.
Jonker, C., Kremer, R., van Leeuwan, P., Pan, D., Treur, J. 1998. A Visual Language for the Domain Knowledge of DESIRE. KAW'98: Eleventh Workshop on Knowledge Acquisition, Modeling and Management, Gaines, B., Musen, M. (eds.), Voyager Inn, Banff, Alberta, Canada, 18-23, 1998.
Kremer, R. 1993. A Concept Map Based Approach to the Shared Workspace. MSc. Thesis, Department of Computer Science, University of Calgary, Calgary, Canada.
Kremer, R. 1994. Concept Mapping: Informal to Formal. Third International Conference on Conceptual Structures, Knowledge Representation Workshop. University of Maryland.
Kremer, R. 1995. The Design of a Concept Mapping Environment for Knowledge Acquisition and Knowledge Representation. Banff Knowledge Acquisition Workshop. Banff, Alberta.
Lambiotte, J. G., Dansereau, D. F., Cross, D. R. & Reynolds, S. B. 1984. Multirelational Semantic Maps. Educational Psychology Review 1(4): 331-367.
Lukose, D. 1991. Conceptual Graph Tutorial. Geelong, Australia, Department of Computing and Mathematics, School of Sciences, Deakin University.
Lukose, D. 1995. Using Executable Conceptual Structures for Modelling Expertise. 9th Banff Knowledge Acquisition For Knowledge-Based Systems Workshop (KAW'95), Banff Conference Centre, Banff, Alberta, Canada.
Marks, J. 1991. A Formal Specification Scheme for Network Diagram That Facilitates Automated Design. Journal of Visual Languages and Computing 2(4): 395-414.
Maurer, F. 1996. Coordinating System Development Processes. KAW'96: Tenth Workshop on Knowledge Acquisition, Modeling and Management, Gaines, B., Musen, M. (eds.), Voyager Inn, Banff, Alberta, Canada, November 8-14, 1996. http://ksi.cpsc.ucalgary.ca/KAW/KAW96/maurer/maurer.html .
McNeese, M. D., Zaff, B. S., Peio, K. J., Snyder, D. E., Duncan, J. C. & McFarren, M. R. 1990. An Advanced Knowledge and Design Acquisition Methodology for the Pilot's Associate. Wright-Patterson Air Force Base, Ohio, Harry G. Armstrong Aerospace Medical Research Laboratory.
Munday, C., Cross, J., Daengdej, J. & Lukose, D. 1996. CGKEE: Conceptual Graph Knowledge Engineering Environment User and System Manual. Armidale, N.S.W., Australia, Department of Mathematics, Statistics, and Computing Science, University of New England.
Myers, B. A. 1990. Taxonomies of Visual Programming and Program Visualization. Journal of Visual Languages and Computing 1(1): 97-123.
Nosek, J. T. & Roth, I. 1990. A Comparison of Formal Knowledge Representation Schemes as Communication Tools: Predicate Logic vs. Semantic Network. International Journal of Man-Machine Studies 33: 227-239.
Novak, J. D. & Gowin, D. B. 1984. Learning How To Learn. New York, Cambridge University Press.
Petre, M. & Green, T. R. G. 1993. Learning to Read Graphics: Some Evidence that 'Seeing' an Information Display is an Acquired Skill. Journal of Visual Languages and Computing 4(1): 55-70.
Price, B. A., Baecker, R. M. & Small, I. S. 1993. A Principled Taxonomy of Software Visualization. Journal of Visual Languages and Computing 4(3): 211-266.
Quillian, M. R. 1968. Semantic memory. Semantic Information Processing. M. Minsky. Cambridge, Massachusetts, MIT Press: 216-270.
Roberts, D. D. 1973. The Existential Graphs of Charles S. Peirce. The Hague, Mouton & Co. N. V.
Shneiderman, B. 1986. Direct Manipulation: A Step Beyond Programming Languages. IEEE Computer 16: 57-69.
Smith, D. C. 1977. Pygmalion: A Computer Program to Model and Stimulate Creative Thought. Stuttgart, Basel.
Sowa, J. F. 1984. Conceptual Structures: Information Processing in Mind and Machine. Reading, Massachusetts, Addison-Wesley.
Wang, D. & Lee, J. R. 1993. Visual Reasoning: its Formal Semantics and Applications. Journal of Visual Languages and Computing 4(4): 327-356.