Abstract. This paper presents three approaches to the representation of processes in the conceptual graph theory, and compares them. Lukose and Mineau each extend the original proposition of John Sowa, with different objectives. Lukose's approach is more oriented toward the graphical representation of processes so that the knowledge engineerís task would be facilitated; while Mineauís approach is more oriented toward the automatic translation of algorithms into an executable but declarative format. Both approaches are somewhat complementary; their similarities will be discussed.1. Introduction
Knowledge representation formalisms like Frames (Minsky, 1975), Partitioned Nets (Hendrix, 1975), Conceptual Dependency Graphs (Schank, 1975), and Conceptual Graphs (Sowa, 1984) represent declarative information. These notations by themselves are insufficient for doing computation, solving problems, and simulating events and processes in such a way as to induce change onto the description of a system. Some form of truth-maintenance inference engine is required for this purpose. Some of the more traditional graph notation developed in Artificial Intelligence (AI) for representing procedural information include the PLASMA system (Hewitt, 1977) and Petri Nets (Petersen 1981). In the PLASMA system, a network of actors pass messages to one another. An actor is a process that responds to messages by performing some services and then by generating messages that it passes to other actors. Petri Nets were originally designed to represent parallel computation by passing tokens from one active element to another.
In recent years, many efforts were directed towards the development
of knolwedge management tools based on conceptual graphs. Some of the more
notable ones include the Deakin Toolset (Lukose, 1991; Garner, Tsui, and
Lukose, 1997), the CoGITo Workbench (Haemmerle, 1995), and the CGKEE system
(Munday et al., 1996). In addition, considerable efforts have been directed
to the development of executable conceptual structures based on conceptual
graphs, as listed in Table 1.
| Authors | Executable Systems based on Conceptual Graphs |
| Sowa (1984) | Actors and Dataflow Diagrams |
| Nagle (1986) | CONGENT: Conceptual Agent |
| Hartley (1986) | Actor Graphs |
| Delugach (1992) | Dynamic Conceptual Graphs |
| Lukose (1992) | ECS: Executable Conceptual Structures |
| Mineau (1996) | CPE: A Conceptual Programming Environment |
| Lukose (1996) | MODEL-ECS: Executable Conceptual Modelling Language |
| Kabbaj and Frasson (1995) | Actors |
| Bos, et al., (1997) | Executable Conceptual Graphs implemented on CoGITo platform |
| Raban and Delugach (1997) | Animating Conceptual Graphs |
As described by (Sowa, 1984), which is also evident today, although the graphs for doing computation have been developed by different people for different purpose, they share the following common themes:
The outline of this paper is as follows. In Sections 2, 3 and 4, detailed implementation and execution of each of the three executable models will be outlined, respectively. In Section 5, we conduct a comparative study on these three models and provide a brief conclusion to this paper.
2. Actor and Dataflow Diagram
2.1. Definition
Sowa (1984) carried out a methodical development of a formalism for graphs of actors that are bounded to conceptual graphs. As a conceptual graph is constructed by joining smaller graphs, actor nodes attached to the conceptual graphs are also joined to form a dataflow graph. Then, control maps on the graph are used to trigger the actors and compute referents for generic concepts. Control marks are drawn in the referent field after the colon in the concept node. Control marks direct the flow of a computation. There are three types of control marks:
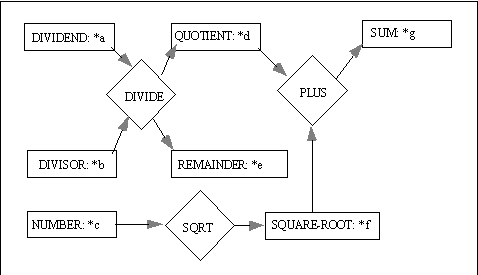
A dataflow graph is a finite, connected, directed, bipartite graph with one set of nodes called concepts, and the other set of nodes called actors. If an arc is directed from a concept c to an actor t, then the arc is called an input arc of t, and c is called an input concept of t. On the other hand, if an arc of a dataflow graph is directed from an actor t to a concept c, then the arc is called an output arc of t, and c is called an output concept of t. Every actor must be attached to at least one arc (either input or output). The arcs of a dataflow graph are drawn as dotted lines to distinguish them from the arcs of conceptual graphs. The concepts are still drawn as boxes, but the actors are drawn as diamonds. Consider the dataflow graph in Figure 1. There are three actors: <DIVIDE>, <PLUS>, and <SQRT>, and six concepts: DIVIDEND, DIVISOR, QUOTIENT, REMAINDER, SQUARE-ROOT, and SUM (all are subtypes of NUMBER; they are role types, which represent a particular way of using the natural type NUMBER). The actor <DIVIDE> has input concept *a of type DIVIDEND and *b of type DIVISOR, and output concept *d of type QUOTIENT and *e of type REMAINDER. The actor <SQRT> has [NUMBER: *c] as input and [SQUARE-ROOT: *f] as output, and <PLUS> has *d and *f as input and [SUM: *g] as output. In conventional programming language, the following statements would generate the same results as this dataflow graph:

A concept c in a dataflow graph v is called: a) a source concept of v it it is an input concept of one or more actors, but not an output concept of any actor, b) a sink concept of v if it is an output concept of exactly one actor, but not an input concept of any actor, c) an intermediate concept of v if it is an output concept of exactly one actor and an input concept of one or more actors, or d) a conflicting concept of v if it is an output concept of two or more actors. In Figure 1, *a, *b and *c are known as source concepts as they are only used as input to actors, *e and *g are sink concepts as they are only used as outputs of actors, *d and *f are intermediate concepts as they are used as both input and output concepts.
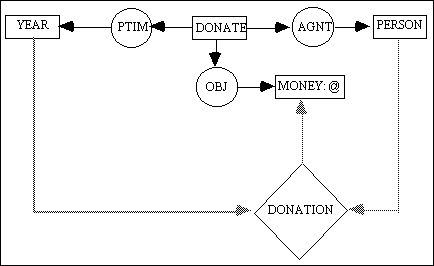
If all concepts in a dataflow graph u are also concepts of a conceptual graph v, then u is said to be bounded to v. If no concepts of the dataflow graph u are concepts of any conceptual graph, then u is said to be free. For example, consider the schema below:
schema for DONATE (x) is v [DONATE: *] - (AGNT) -> [PERSON] (OBJ) -> [MONEY: @] (PTIM) -> [YEAR]and the following dataflow graph:
<DONATE> - u <- [PERSON] <- [YEAR] -> [MONEY: @]One could bound the above dataflow graph to the schema for DONATE to produce a dataflow graph as shown in Figure 2. This dataflow graph is considered to be bounded to the schema for DONATE. On the other hand, Figure 1 is a free dataflow graph. The dataflow graph in Figure 2 computes the amount of money that was donated by a [PERSON: *p] in a particular [YEAR: *y]. Thus, this <DONATION> actor has two input parameters and a single output parameter. Assuming that the information about all donations are kept in a database relation called DONATE, then the <DONATION> actor may be implemented as an SQL query of the following form1:
SELECT MONEY FROM DONATION WHERE PERSON = *p AND YEAR = *y.
2.2. Implementation of the Factorial function
The "factorial" is a recursive function that takes as its input a positive
number and computes its factorial value. Figure 3 lists the pseudo
code for this function. The IDENT function takes as input one argument,
and produces an output which is the same as its input value.
function FACTORIAL (N, O) begin if IDENT(N) = 0 then O := N + 1; else if IDENT(N) > 0 then begin N' := N -1; FACTORIAL (N', J); O := N * J; end; end. |
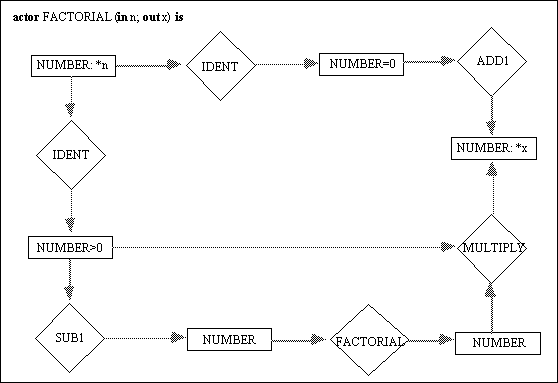
The pseudo code in Figure 3, can be defined recursively using the actors <IDENT>, <ADD1>, <SUB1>, and <MULTILY>, as shown in Figure 4. The concepts have subrange types NUMBER>0 and NUMBER=0, for simplicity reasons. Assuming that we have 2 as the input for this <FACTORIAL> actor as shown below:
The actor is evaluated by replacing it with a copy of its defining graph (Figure 3), and replace the formal parameter *n with the value and assertion mark (2!). Both IDENT actors are now ready. The upper one is blocked because it would compute the value 2, which does not conform to the type label NUMBER=0. The lower one is enabled. When it fires, it erases the assertion mark on its input and changes its output concept to [NUMBER>0: 2!]. This enables the <SUB1> actor to fire. Its output becomes [NUMBER: 1!]. The input of <SUB1> loses its assertion mark, but it retains the value 2, which will be used later by <MULTIPLY>. Now, the recursive <FACTORIAL> is fired again, as follows:
Once again, the upper <IDENT> is blocked, but the lower <IDENT> fires, erases the assertion mark on its input, and changes its output concept to [NUMBER>0: 1!]. This enables <SUB1> to fire; the input of <SUB1> looses its assertion mark but it retains the value 1, which will be used later by <MULTIPLY>. Now, the recursive <FACTORIAL> is fired again, as follows:
With the new input 0!, the upper <IDENT> will fire, with output changed to [NUMBER=0: 0!]. This will enable <ADD1> to fire, giving its output to be [NUMBER: 1!]. This will enable the output of "c" to be:
Then the <MULTIPLY> actor will fire, thus effectively doing 1 * 1, giving [NUMBER: 1!]. This will effectively produce the output of "b" to be 1, a follows:
This will now, enable the <MULTIPLY> to fire, thus effectively doing 2 * 1, giving [NUMBER: 2!]. This will effectively produce the output of "a" to be 2, as follows:
The execution terminates at this point, the answer being 2.
3. Mineauís Representation of Dynamic Processes
3.1. Definition
(Mineau, 1996) proposes a representation for dynamic processes which has five objectives: 1) to allow the automatic execution of processes, 2) to incorporate declarative and dynamic knowledge in order to support the implementation of a Conceptual Programming Environment (CPE), 3) to avoid human intervention in the execution of processes, 4) to be as simple as can be in order to facilitate the application developerís task, and 5) to allow the automatic validation of processes. This representation proposes an extension to the definition of actors as originally proposed in (Sowa, 1984), and is also based on earlier work by (Delugach, 1991).
Basically, the main idea is to view an actor as a state transition mechanism: from fulfilled preconditions, the actor is fired, and its postconditions are asserted. The pre and postconditions being a conjunction of conceptual graphs, this definition, though similar to the one found in (Sowa, 1984), is more general, and provides a framework which improves tremendously the representational power of the CG theory. Figure 5 shows a simple example of an actor, where g1, g2, g3 and g4 are conceptual graphs.

The graph of Figure 5 states that actor *a will be triggered (will fire) if, from the current state of the system, graphs g1 and g2 are both true (are logical consequences of the actual state of the system). In this case, two assertions will be made: g3 will be asserted and g4 will be negated (i.e., ¬g4 will be asserted). Of course, there may be problems with this state transition: g3 may not be valid according to the semantic constraints of the system2. Also, this may trigger thorough knowledge revision activities: g4 may not be easily negated (because of previous assertions and stated rules)3. In that case, the actor is blocked and the user is notified. It may also be the case that an actor does not change the current state of the system (if g3 is already true and g4 already false for instance).
It is clear from our model, that the input to an actor is composed of complete conceptual graphs, called input graphs, and not just input concepts as proposed in (Sowa, 1984), and that the output from an actor is also composed of conceptual graphs, called output graphs, either asserted or negated, and not just instantiations of generic concepts, as proposed in (Sowa, 1984). Furthermore, let us mention that the concepts in any graph, either input or output graph, can be coreferenced to any other concept in the knowledge base: we make the assumption that coreference in global. So a concept in an input graph can be represented in an output graph as well. Actors that trigger change on concepts need to refer to these concepts in both their input and output graphs.
The other main difference between this representation and what is proposed in (Sowa, 1984) concerns the sequencing mechanism. Sowaís proposal implements an explicit token passing mechanism which supposes some interaction with the user to send the initial tokens. With simple actors as those of Section 2 above, this is not a problem. However, in the general case, it may be problematic to find all the actors which need to be initially triggered in order to accomplish some task correctly (without deadlocks for instance). Generally, we think that the user should not have to interact with the actors in order to produce the right execution sequence; the user should only start the process and the initial tokens should automatically be sent to the relevant actors. Also, in the construction of a CPE, we do not wish to complexify the execution control mechanism. The only mechanism we wish to implement is a precondition checking mechanim. Keeping that in mind, we propose to represent the execution sequence using predicates that will be incorporated into the preconditions of the relevant actors. Doing so, the execution control mechanism we need in order to implement our CPE is the precondition checking mechanism which needed to be developed anyhow. Making sure that each execution sequence is identified by its own unique predicate, the user does not have to know about the sequencing structure of the process in order to engage it. Consequently, each actor will include preconditions needed by the sequencing mechanism of the process it takes part in.
3.2. Implementation of the Factorial function
As mentioned above, a process will be represented as a set of actors
linked by an execution sequence explicitly described by predicates in their
pre and postconditions. When the preconditions of an actor become conjunctively
true, its postconditions will be asserted, updating the current state of
the system. Since any algorithm uses a small set of well-defined state
transition operators, it is very easy to automatically translate each of
them into a set a pre/postcondition pairs. For instance, mathematical operators
on variables will be implemented using basic actors (as presented in Section
2 above); they represent external procedures which compute some output
value from their operands. Variable assignments will be represented by
two pre/postconditions pairs: one for the case where the newly assigned
value differs from the previous value of the variable, the other, for the
case where the newly assigned value is identical to the previous value
of the variable. All sequencing instructions such as if-else and loops
will be implemented using the synchronization predicates which will be
added to the pre and postconditions of sequence-related actors. In order
to produce the synchronization predicates, the algorithm is analyzed and
a synchronization graph is produced. Figure 6 below shows our version
of the factorial problem using C; Figure 7 shows the corresponding
synchronization graph.
l0: int fact(int n)
l1: { int temp;
l2: int ftemp;
l3: int f;
l4: if (n == 0 or n == 1)
l5: f = 1;
l6: else
l7: { temp = n - 1;
l8: ftemp = fact(temp);
l9: f = n * ftemp;
l10: }
l11: return f;
l12: }
|
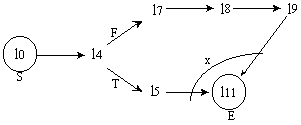
All algorithms will be required to have unique entry and exit points, as shown in the synchronization graph of Figure 7, with the S (start) and E (end) nodes. This hides the synchronization details from the user who will need to trigger only the entry node of the synchronization graph in order to engage the process. All synchronization predicates (tokens) will be instantiated in the proper execution order from that point on. The arc labeled x is used to denote an exclusive-or between two pathways leading from l4 to l11, since their selection is based on the evaluation of a boolean condition in line l4. This implies that the instruction of line l11 must be represented by two different pre/postconditions pairs, one for each possible pathway. Normally, different edges reuniting at a node imply a conjunction of preconditions. In this case, it represents a disjunction of preconditions. All other links are set based on the dependencies between the instructions which use the variables of the algorithm, and those which update them. In this example, such dependencies are fairly simple to identify; we will not explain them any further at this time.
In the remainder of this section, we go through the entire example of Figure 6 in order to show how each instruction is automatically translated into a set of pre/postconditions pairs, based on the synchronization graph of Figure 7.
line l0: the entry point of a function
With our representation, input values to a function may be any information relevant to the process achieved by the function. This means that any cg could be used as an input parameter to a function (or process). We need a way to identify how cgs can be exchanged between functions. For that purpose, we define that the input parameters of a function, the cgs expected by a function, will appear in the preconditions of the first transition rule (the one associated with line l0). In our example, rule 0 is the first rule of our process4. Consequently, its precondition will include a cg describing the information that is expected from the calling function. For now, let this cg be the first graph encountered in the precondition of rule 0 (pre0). Coreference links from this graph to any other graph in the process description allows the passing of the appropriate (input) values to other graphs. Hence, the value of the variable n will be called y1 throughout the whole description of the process5.
pre0:
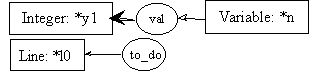
post0:
line l4: if (n ==
0 or n == 1)
Selections are like iterations since the block of instructions to execute next is determined based on the evaluation of a boolean expression. Consequently, the postconditions of its transition rules will set the status of all instructions in the selected block to ìto doî, including the instruction at the crossroad of both pathways (line l11 in our example, see Figure 7). If other instructions followed line l11 in our algorithm, then the postconditions of line l11 would have to set their status to ìto doî.
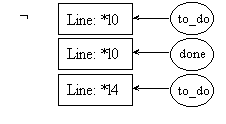
pre4.1:
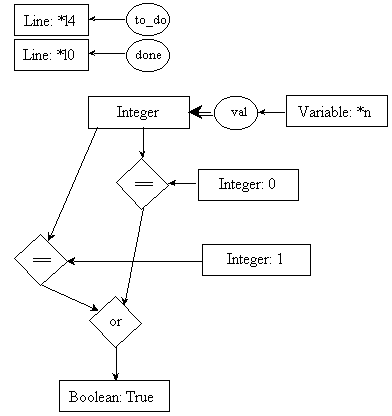
post4.1:
pre4.2:
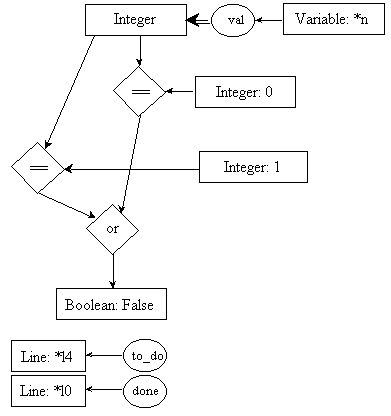
post4.2:
line l5: f = 1;
pre5.1:
post5.1:
pre5.2:
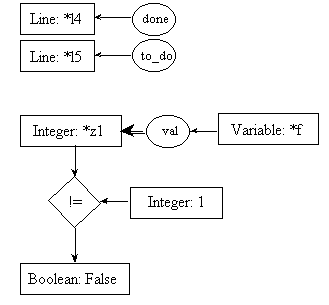
post5.2:
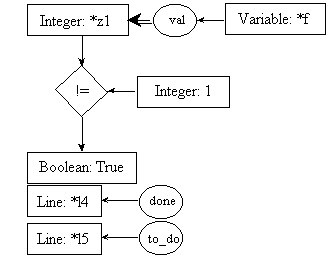
line l7: temp = n - 1;
pre7.1:
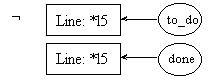
post7.1:
pre7.2:
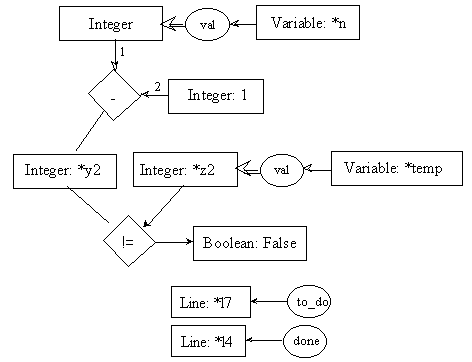
post7.2:
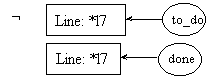
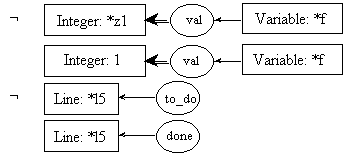
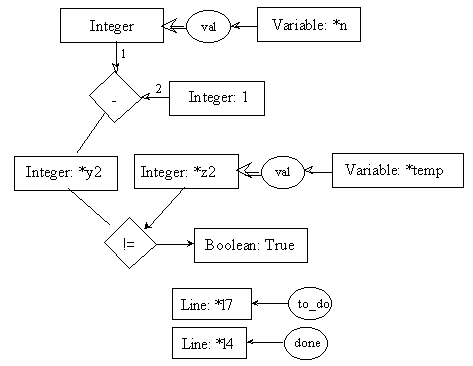
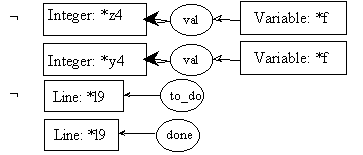
line l8: ftemp = fact(temp);
Here, fact is a function; it can be represented as a process. In fact, thatís our current goal. As said before, input and output parameters must be identified so that information between the current process and the new process could be exchanged. This information is represented using cgs. To identify the parameters of the process, we will use a box (representing a context). Each box will contain exactly one cg. There will be one box for each parameter. Boxes representing input parameters, called input boxes, will point toward the process; boxes representing output parameters, called output boxes, will point away from the process. The arcs linking the parameters to the process will be numbered to avoid confusion. The process itself will be represented by a double-lined diamond box. In our example, fact is a process, and is thus represented graphically as a double-lined diamond box. It has one input parameter, which is a cg stating that we need the value of an integer variable to start the process; it has one output parameter which is an integer number, which will be used in other computations after the process produces it. Please notice that the input parameter of the process fact is a cg similar to the first cg found in pre0 which was set to be the input parameter (the formal parameter) of the process being described (fact). The parameter in the input box below is said to be the effective parameter used to call the process. It is thus consistent that these two cgs would be similar.
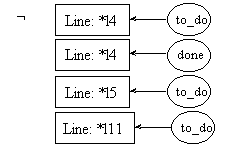
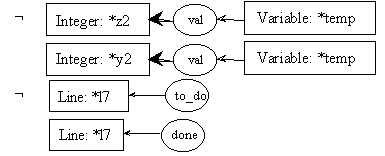
pre8.1:
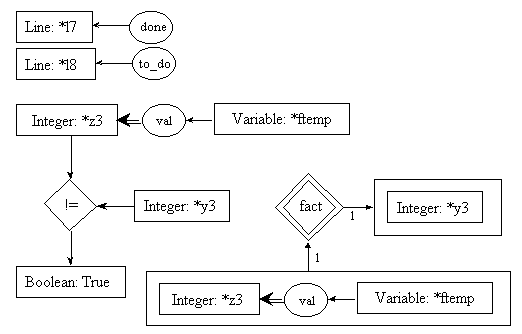
post8.1:
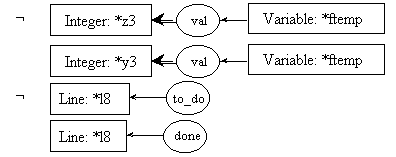
pre8.2:
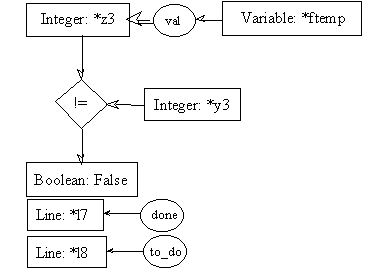
post8.2:
Since we know that the preconditions of rules 8.1 and 8.2 will be both evaluated, and since coreference links are enforced throughout the whole process description, it is needless to repeat the call to fact in pre8.2. The one in pre8.1 will suffice to instantiate the [Integer: *y3] concept in both preconditions.
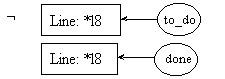
line l9: f = n * ftemp;
pre9.1:

post9.1:
pre9.2:
post9.2:
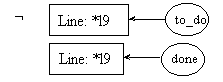
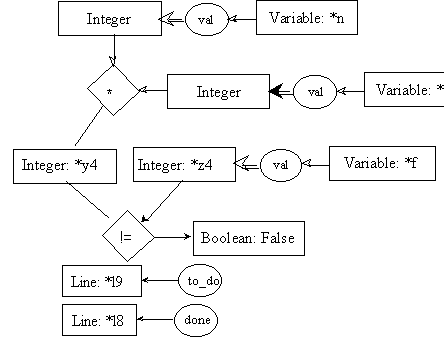
line l11: return f;
Since the output parameter of the fact function is a single concept (an integer value), its origin must be identified. Rules 11.1 and 11.2 below use their precondition part to identify its origin, while the coreference mechanism will instantiate the very last cg of their postconditions. We will define for now that the last cg of both postconditions represent the output parameter of the function.
pre11.1:
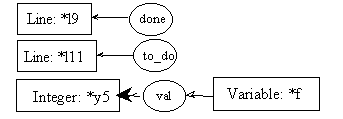
post11.1:
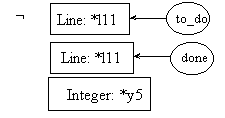
pre11.2:
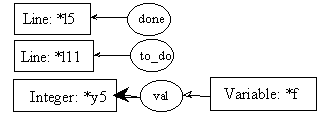
post11.2:
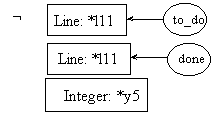
The reader should notice that the last cg in the last two rules concur with the output graph of the fact process (see pre8.1); while the first graph of rule 0 is similar to the input graph of the fact process (also shown in pre8.1). Parameter evaluation and value passing mechanisms fall outside the scope of this paper, but are described in details in (Mineau, 1996).
In summary, this Factorial function could be defined as in Figure 8. This definition could be produced either by the automatic analysis of the algorithm of Figure 6, or manually. This definition implies that the input graphs (here u1, the first graph of pre0) will be part of the preconditions of rule 0, and that the output graphs (here u2, the last graph of rule 11) will be part of the postconditions of rule 11 (post11.1 and post11.2). Figure 9 gives the schematic description of a process.
4. MODEL-ECS
4.1. Definition
MODEL-ECS is an executable conceptual modelling language that is based on conceptual graphs and actors (Lukose, 1996). The implementation of the actors (or more accurately known as actor graphs) in this modelling language differs considerably from that of Sowa's (Section 2). In MODEL-ECS, we make a distinction between an actor and an actor graph. An actor is similar to class definitions in conventional object-oriented modelling languages; it defines the interface (i.e., messages that instances of this actor can handle, and its associated methods). To define an actor graph, one has to firstly define the Actor Type, and the Concept Type. Then, by combining these two forms of abstractions, together with the precondition, postcondition, and a delete list of conceptual graphs, as shown in Figure 10, we are able to define an actor graph of a particular type.
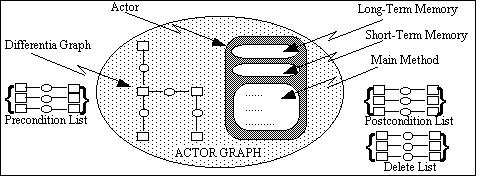
The main ingredients for modelling executable constructs are: actor graphs, problem maps (described in Lukose, 1993, 1996, 1997, at various levels of detail), conceptual relations to enable the expression of temporal relationships, and special purpose actor graphs for expressing condition and iteration. Table 2 lists some of the basic conceptual constructs predefined in MODEL-ECS.
| Conceptual Constructs | Descriptions |
| (FBS) | Conceptual Relation to indicate sequence. |
| (SWS) | Conceptual Relation to indicate concurrence. |
| [PM] | Concept to represent Problem Map. |
| [KS] | Concept to represent Knowledge Source. |
| [TRUE_TEST] | Actor Graph to indicate positive test. |
| [FALSE_TEST] | Actor Graph to indicate negative test |
| [LT] | Actor Graph to check less than condition. |
| [GT] | Actor Graph to check greater than condition. |
| [LTEQ] | Actor Graph to check less than or equal to condition. |
| [GTEQ] | Actor Graph to check greater than or equal to condition. |
| [ASSERT] | Actor Graph to assert a predicate into the working memory. |
| [RETRACT] | Actor Graph to retract a predicate from the working memory. |
| [INCREMENT] | Actor Graph to increment a variable predicate. |
| [DECREMENT] | Actor Graph to decrement a variable predicate |
Assuming that f and j
denote ordinary predicates (i.e., conceptual graphs), x
denote a variable predicate, m and n
are numbers, and a and b
denote Problem Maps, the above conceptual constructs can be used to construct
simple Problem Maps shown in Table 3.
| Syntactic Representation | Semantics |
| [PM: a] -> (FBS) -> [PM: b] | Do a followed by b |
| [PM: { [PM: a], [PM: b] }] | Do either a or b, non deterministically. |
| [TRUE_TEST: f ] | Proceed if f is true. |
| [FALSE_TEST: f ] | Proceed if f is false. |
| [LT] ->(OP1)->[NUMBER:m]
->(OP2)->[NUMBER:n] |
Proceed if m is less than n. |
| [GT] ->(OP1)->[NUMBER:m]
->(OP2)->[NUMBER:n] |
Proceed if m is greater than n. |
| [LTEQ] ->(OP1)->[NUMBER:m]
->(OP2)->[NUMBER:n] |
Proceed if m is less than or equal to n. |
| ETEQ] ->(OP1)->[NUMBER:m]
->(OP2)->[NUMBER:n] |
Proceed if m is greater than or equal to n. |
| [ASSERT: f ] | Proceed after successfully asserting the predicate f into the working memory (applies to both ordinary and variable predicate). |
| [RETRACT: f ] | Proceed after successfully retracting the predicate f from the working memory (applies to both the ordinary and variable predicate). |
| [INCREMENT: x ] | Proceed after successfully incrementing the numeric value associated with the variable predicate x. |
| [DECREMENT: x ] | Proceed after successfully decrementing the numeric value associated with the variable predicate x. |
Using the simple modelling constructs outlined in Table 3, we are
able to build more complex modelling constructs as shown in Table 4.
Again, we assume that f and j
are predicates (i.e., conceptual graphs), while a
and b are problem maps.
| Modelling Construct | Executable Conceptual Structure Representation |
a;b |
[PM: a ] -> (FBS) -> [PM: b ] |
if f then a else b |
[PM: { [KS: [TRUE_TEST: f ] ] -> (FBS) -> [PM: a ],
[KS: [FALSE_TEST: f ] ] -> (FBS) -> [PM: b ]
}
]
|
while f do a |
[PM: { [KS: [TRUE_TEST: f ] ] -> (FBS) -> [PM: a ] -
-> (FBS) -> [PM:*],
[KS: [FALSE_TEST: f ] ]
}
]
|
repeat a until f |
[PM: a ] -> (FBS) -> [PM: { [KS: [FALSE_TEST: f ] ] -> (FBS) -> [PM: a ],
[KS: [TRUE_TEST: f ] ]
}
]
|
case f : a, j : b |
[PM: { [KS: [TRUE_TEST: f ] ] -> (FBS) -> [PM: a ],
[KS: [TRUE_TEST: j ] ] -> (FBS) -> [PM: b ]
}
]
|
for x = y to z do a |
[PM: [KS: [ASSERT: [VARIABLE: x]->(EQ)->[NUMBER:y] ]
] ->(FBS) -> [PM: { [KS: [GT] ->(OP1) ->[NUMBER: x]
->(OP2)-> [NUMBER: z]
],
[PM: a ] -> (FBS) -> [KS: [INCREMENT: [VARIABLE: x]
->(EQ)->[NUMBER]
]
] -> (FBS) -> [PM: *]
}
] -> (FBS) -> [KS: [RETRACT: [VARIABLE: x] ->(EQ) -> [NUMBER]
]
]
]
|
4.2. Implementation of the Factorial function
To implement the FACTORIAL function shown in Figure 3, we have to
implement the following actor: IDENT, ADDITION, SUBTRACT, and MULTIPLY.
There are two types of IDENT actors. They are IDENT1 and IDENT2, with argument
conforming to [NUMBER=0] and [NUMBER>0], respectively. Note that both [NUMBER=0]
and [NUMBER>0] are subtypes of [NUMBER]. Their definition are shown below:
actor IDENT1 (*x) is [ACT] -> (ARG) -> [NUMBER=0: *x] -> (RSLT) -> [NUMBER: *x]
actor IDENT2 (*x) is [ACT] -> (ARG) -> [NUMBER>0: *x] -> (RSLT) -> [NUMBER: *x]
actor ADDITION (*x, *y, *z) is [ACT] -> (ARG1) -> [NUMBER: *x] -> (ARG2) -> [NUMBER: *y] -> (RSLT) -> [NUMBER: *z]
actor SUBTRACT (*x, *y, *z) is [ACT] -> (ARG1) -> [NUMBER: *x] -> (ARG2) -> [NUMBER: *y] -> (RSLT) -> [NUMBER: *z]
actor MULTIPLY (*x, *y, *z) is [ACT] -> (ARG1) -> [NUMBER: *x] -> (ARG2) -> [NUMBER: *y] -> (RSLT) -> [NUMBER: *z]By using the above actors and the IF-THEN-ELSE construct outlined in Table 4, we can recursively define the problem map FACTORIAL as shown in Figure 11.

5. Discussion and Conclusion
Basically, both proposals (of Sections 3 and 4) are extensions of Sowaís original proposal, and thus, offer more expressiveness. Both allow system updates in the form of assertions and negations (represented by a delete list in Section 4). Lukoseís work focuses on the graphical aspect of process modeling, and pinpoints implementation details such as memory organization, which would support such a system. Mineauís approach focuses more on the conceptual representation of a process in a state transition machine. It advocates automatic translation of a process description from a linear algorithmic modeling language to a logical representation language. Both approaches allow processes to be executed; both approaches allow parallelism in the execution of a process.
However, the graphical nature of the formalism proposed by Lukose offers advantages when interacting with an application modeler who must devise a process; while Mineauís approach is obviously simpler when this process has already been devised and is ready to be described, and when it can be described using algorithmic primitives (as is the case with the factorial function). In effect, the breakdown of a process into a set of transition rules results in the loss of the structure of the process itself. For problems which are described using higher-level primitives (not available in conventional programming languages), or whose description must be refined from time to time (e.g., when first described), it may be beneficial to the application modeler to use a graphical notation which explicitly shows the structure of the process and its relation to other processes. When describing a complex problem, such a graphical notation may help the application modeler to visualize the structure of the process, to discover the deep nature of the process or of its relations with other processes. This may entail refinements that would not occur if a linear notation were used (as with conventional programming languages).
Consequently, we see both approaches as being complementary. For elicitation purposes, Lukoseís approach could be used to obtain a first model of a process. This conceptual graph could then be analyzed to produce a set of transition rules (as with Mineauís approach). Of course, in order to produce the exact set of pre and postconditions representing the synchronization structure of the process, additionnal elicitation may be required, forcing the application modeler to refine his/her initial model. Iterations between graphical elicitation of the process and its automatic translation into a logical form would go on until the precision of the model would be sufficient enough to make its final translation into a set of transition rules.
6. References
Bos, C., Botella, B., and Vanheeghe, P., (1997). Modelling and Simulating Human behaviours with Conceptual Graphs, in Proceedings of the Fifth International Conference on Conceptual Structures Seattle, WA., (appeared as LNAI 1257, Conceptual Structures: Fulfilling Peirce's Dream, D. Lukose, H. Delugach, M. Keeler, L. Searle, and J. Sowa (eds.)), pp. 275 - 289.
Delugach, H. (1991). Dynamic Assertion and Retraction of Conceptual Graphs. In: Proc. of the 6th Annual Workshop on Conceptual Graphs. E. Way (ed.). SUNY at Binhamton. July. 15-26.
Delugach, H.S. (1992). Specifying Multiple-Viewed Software Requirements With Conceptual Graphs. Jour. Systems and Software 19:207-224.
Garner, B.J., Tsui, E., and Lukose, D., (1997). Deakin Toolset: Conceptual Graphs Based Knowledge Acquisition, Management, and Processing Tools, in Proceedings of the Fifth International Conference on Conceptual Structures (ICCS'97), Seattle, WA., (appeared as LNAI 1257, Conceptual Structures: Fulfilling Peirce's Dream, D. Lukose, H. Delugach, M. Keeler, L. Searle, and J. Sowa (eds.)), pp. 589 - 593.
Haemmerle, O., (1995). CoGITo: Une plate-forme de developpement de logiciels sur les graphes conceptuels, PhD thesis, University Montpellier2.
Hartley, R.H., (1986). The Foundation of Conceptual Programming, in Proceedings of the First Annual Rockey Mountain Conference on Artificial Intelligence, Boulder, Colorado, USA.
Hendrix, G.G., (1975). Expanding the utility of Semantic Networks through Partitioning, in Proc. IJCAI-75, pp. 115-121.
Hewitt, C., (1977). Viewing Control Structure as Patterns of Passing Messages, Artificial Intelligence, 8, pp. 323-364.
Kabbaj, A., and Frasson, C., (1995). Dynamic CG: toward a general model of computation. In: Supplementary proceedings of iccs-95, 3rd Int. Conf. On Conceptual Structures: Applications, Implementation and Theory. G. Ellis, R. Levinson, & B. Rich (eds). University of California at Santa Cruz. 46-60.
Lukose, D., (1991). Conceptual Graph Tutorial, Department of Computing and Mathematics, Faculty of the Sciences, Deakin University, Geelong, Victoria, 3217, Australia.
Lukose, D., (1992). Goal Interpretation as A Knowledge Acquisition Mechanism, PhD Thesis, Department of Computing and Mathematics, Deakin University, Geelong, Australia.
Lukose, D., (1993). Executable Conceptual Structures, in Proceedings of the First International Conference on Conceptual Structures (appeared as LNAI-699, Conceptual Structures: Conceptual Graphs for Knowledge Representation, Guy Mineau, Bernard Moulin, and John Sowa (eds.), Springer-Verlarg, Germany), Quebec City, Quebec, Canada.
Lukose, D., (1996). MODEL-ECS: Executable Conceptual Modelling Language, in Proceedings of the 10th Workshop on Knowledge Acquisition for Knowledge Based Systems, Banff, Canada.
Lukose, D., (1997). Complex Modelling Constructs in MODEL-ECS, in Proceedings of the Fifth International Conference on Conceptual Structures Seattle, WA., (appeared as LNAI 1257, Conceptual Structures: Fulfilling Peirce's Dream, D. Lukose, H. Delugach, M. Keeler, L. Searle, and J. Sowa (eds.)), pp. 228 - 243.
Mineau, G.W., (1994). Views, Mappings and Functions: Essential Definitions to the Conceptual Graph Theory. In: Conceptual Structures: Current Practices. Proc. of the 2nd Int. Conf. on Conceptual Structures (ICCS-94). Lecture Notes in Artificial Intelligence #835. W.M. Tepfenhart, J.P. Dick & John F. Sowa (éds). Springer-Verlag. 160-174.
Mineau, G.W., (1996). The Representation of Dynamic Process using Conceptual Graphs, Final Report #960611B, Project P2, Deliverable B (unpublished).
Mineau, G.W. & Missaoui, R., (1996). Semantic Constraints in Conceptual Graph Systems. Le Groupe Conseil DMR Inc. R&D Division. Internal Report #960611A.
Mineau, G.W. & Missaoui, R., (1997). The Representation of Semantic Constraints in CG Systems. In: Conceptual Structures: Fulfilling Peirceís Dream. Proc. of the 5th Int. Conf. on Conceptual Structures (ICCS-97). Lecture Notes in Artificial Intelligence #1257. D. Lukose, H. Delugach, M. Keeler, L. Searle & J.F. Sowa (éds). Springer-Verlag. 138-152.
Minsky, M., (1975). A Framework for Representing Knowledge, in The Psychology of Computer Vision, Winston, P.H., (Ed.), MCGraw-Hill, MA.
Munday, C., Cross, T., Daengdej, J., Lukose, D., (1996). CGKEE: Conceptual Graph Knowledge Engineering Environment User and System Manual, Technical Report, School of Mathematical and Computer Science, The University of New England, Armidale, 2350, N.S.W., Australia.
Nagle, T.E., (1986). Conceptual Graphs in an Active Agent Paradigm, in Proceedings of the IBM Workshop on Conceptual Graphs, Thornwood, USA.
Peterson, J.L., (1981). Petri Net Theory and the Modeling of Systems, Prentice-Hall, Englewood Cliffs, NJ.
Raban, R., and Delugach, H.S., (1997). Animating Conceptual Graphs, in Proceedings of the Fifth International Conference on Conceptual Structures (ICCS'97), Seattle, WA (appeared as LNAI 1257, Conceptual Structures: Fulfilling Peirce's Dream, D. Lukose, H. Delugach, M. Keeler, L. Searle, and J. Sowa (eds.)), pp.431 - 445.
Schank, R.C., ed. (1975). Conceptual Information Processing, North-Holland, Amsterdam.
Sowa, J.F., (1984). Conceptual Structures: Information Processing in
Mind and Machine, Addison Wesley, Reading, Mass.