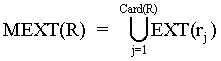
1 INTRODUCTION

The ripple-down rule approach (RDR) is an expert system methodology whose origin is in the medical expert system GARVAN-ES1 (Compton, Horn, Quinlan, and Lazarus, 1989). From the experience with GARVAN-ES1 maintenance, it became apparent that experts provided their justifications by asserting their judgements correction in such a way that these justifications were strongly influenced by the context where they had been asked to provide it (Compton and Jansen, 1990). Moreover, in justifying why two conclusions differed, the experts distinguished - with no difficulty - the corresponding cases in which they had been produced. In addition, it was noticed that, instead of explaining the way in which a particular conclusion is reached, the experts gave a justification of why this conclusion is right tailored to the specific context. Such a justification is employed in RDR to add rules in the context of when the system arrives at the same wrong conclusion through the same pathway of rules. The so-added new rules are only used in the context in which they were provided. RDR focuses on the maintenance of the system. In this sense, this methodology supplies automated validation with respect to previous cases that had required the addition of new rules.

The RDR approach has proven its efficiency and performance in real world problems. Thus, it has been validated by the development of a large medical expert system, namely, PEIRS (Edwards, Compton, Malor, Srinivasan, and Lazarus, 1993). This system was developed whilst in routine use and has only involved domain experts. However, current RDR-based systems have been criticised because they do not provide any explicit model of the domain knowledge underlying the rule base. Therefore, RDR-based systems limit the potential for re-use and sharing as well as interoperability. In Martínez-Béjar, Benjamins and Martín-Rubio (1997), a set of ontological operators which enable the structured extraction of domain knowledge ontologies from knowledge elicited previously has been proposed. Such operators are, based upon an integration of the so-called knowledge functions-based approach (Martínez-Béjar, Benjamins, Martín-Rubio and Castillo, 1996) and mereological aspects.

The purpose of this paper is to provide RDR-based systems with an ontological framework specifically oriented to the particularities of the RDR approach. The aim is achieved by using the philosophical foundations of the mentioned ontological operators in the context of RDR. More precisely, the ontological vocabulary and the relationships among terms are intended to be supplied by the experts when they want to construct an input case. For doing this, the expert is given a new ergonomic visual framework through which they can form cases and establish/maintain conceptual hierarchies. The motivation for adopting this sort of framework stems from assuming that the experts can easily establish partial conceptual hierarchies containing the domain knowledge underlying a particular case they want to enter to the system.

We have emphasised in making it possible the consistency between the domain knowledge ontology and the domain knowledge contained in the rule base. Although there are other syntactically and semantically well-defined visual languages that allow for the representation, acquisition and edition of knowledge structures (see, for example, Brachman and Schmolze (1985) or Gaines (1991)), our approach has been conceived in a different manner. Thus, for example, the rest of approaches do not address the problem of checking the consistency between the rule base (in our case the RDR base) and the conceptual hierarchy.

On the other hand, there is also some other research concerning the formal techniques-based extraction of ontological vocabulary from RDR systems (Richards and Compton, 1997a; 1997b). However, we argue that experts (and, in general, human beings) accomplish the mental processes (for instance, abstraction) necessary to construct ontologies in a better way.

The structure of the paper is as follows. Section 2 offers a brief overview of the - for this article relevant - aspects of the Ripple-Down Rule approach. In Section 3, we describe a methodology for designing ontological operators from conceptual hierarchies constructed by experts in the context of Ripple-down rules-based systems. Also, it is shown an example where a part of the theory exposed in this Section is applied. Section 4 introduces a set of protocols that guarantee the consistency between knowledge domain ontologies formed by the experts and the knowledge domain underlying the rule base. Section 5 offers the main implementation aspects of the system developed for supporting the approach presented in this work. Finally, in Section 6 we present conclusions.

2 RIPPLE-DOWN RULES

The Ripple-Down Rule (RDR) methodology arose as a result of the maintenance problems with GARVAN-ES1 (Compton, Horn, Quinlan and Lazarus, 1989), which was one of the first four medical expert systems to be put into routine clinical use (Buchanan, 1986). It was used to provide clinical interpretations for reports on the results of measuring thyroid hormones in blood samples (Horn, Compton, Lazarus and Quinlan, 1985). Although GARVAN-ES1 was 96% accurate when it was introduced in 1984, after about two years maintenance the size of the system had doubled and the accuracy reached 99.7%. In other words, a doubling in size was required to take the accuracy from 96% to 99.7%.

RDR has been conceived as a methodology to use all these experts’ behavioural features when they are maintaining a KBS. In particular, RDR focuses on adding a refinement to capture the identified difference instead of attempting to modify the existing knowledge base. The resulting structure of the KBS can be viewed as a binary tree where every node is an "if ..then" rule containing only conjunctions that remember the case which was mis-classified and resulted in the rule being added. These cases are termed "cornerstone cases".

The inference process is a typical example of non-monotonic reasoning in which the conclusion is revised if a further rule is satisfied. Thus, the system starts from the root node so that each traversed rule will be evaluated against the input case. If the rule has been satisfied by the input case, then inference proceeds to one of the two branches (i. e., to the true branch). Otherwise, it will go to the other one (i. e., to the false branch). When there are no more nodes to traverse, the conclusion of the last rule satisfied will be given as the conclusion for that case.

In RDR, when the system provides the conclusion for the input case, additional information is shown, including the rules that were satisfied by the case, the complete sequence of rules that were evaluated and the result of the evaluation, namely, either true or false. At this point, it may occur that the expert disagrees with such a conclusion. Then, The RDR system allows the addition of a new rule, its location being supplied by the trace rule. In particular, in RDR if a new rule is to be added, it will be linked to the last evaluated rule. Moreover, the differences between the input case and the cornerstone case associated to the ultimate true rule in the rule trace assist the expert to select the features for the new rule.

Besides, to add the new rule at the end of the current rule trace ensures that the system will employ the rule in the same context in which it was provided. In this sense, when an expert explains why a particular conclusion is wrong for a specific case, the context includes the case in hand and the expert’s assumption relative to why the trainee who supplied the wrong conclusion made an error. To be precise, the context in which the wrong conclusion was produced is given in RDR by the sequence of rules that were evaluated so that the new rule the expert provides will only be evaluated for another case in the same context (i. e., if the same sequence of rules is followed).

On the other hand, RDR assumes that the domain is a closed world and, hence, a negation which applies to the cornerstone case in the so-called difference list should be satisfied by the input case, this difference list being defined as the union set {x | (x Î input case) and (x Ï cornerstone case)}È {NOT(x) | (x Ï input case) and (x Î cornerstone case)}.

To end with the inference process, the system appends a rule at the end of rule trace in such a way that the conditions are selected by the expert from the difference list along with any common conditions from the intersection.

2.1 Using RDR for Knowledge Acquisition.

RDR can also be viewed as a KA technique. In this sense, when the expert does not agree with a conclusion given by the system, RDR acts by following the next sequence (Kang, 1996):

• The expert enters the correct conclusion.
• The expert is shown the differences between the two cases so that he or she must choose the conditions from these differences in order to justify the new conclusion. In addition to this, the expert is allowed to choose more conditions from the common features.
• The system composes the rule with the selected conditions and the conclusion.
• The system allocates the rule at the end of the rule trace.
• The system adds the input case into the cornerstone case database. In other words, this new case becomes the cornerstone case of the new rule.

So, the KA process in an RDR system allows experts to proceed without knowing anything about the knowledge organisation inside the system. His or her role in this process is limited to entering the correct conclusion for the input case and to select conditions from a list, which in its turn is supplied by the system. This list contains the differences between the input case and the cornerstone case corresponding to the last true rule. In this manner, it is guaranteed that when the expert wants to make a new rule, this will be satisfied only by the input case (but not by any of the other cornerstone cases). To illustrate this, and by assuming that, for example, a given rule (R₅) was the last true rule in the rule trace, the cornerstone case associated to R₅, that is, CC₅, will be chosen by the system to be confronted to the input case in order to obtain the difference list. Suppose also that CC₅ is composed by the conditions {ON_T4, SICK, Sex = male, TSH = high, TSH_BORD = high, T3 = missing, T3_BORD = missing, FTI = high, FTI_BORD = high}. Then, the difference list will be obtained as follows:

Input case                                                              CC₅                                                      Difference list

ON_T4                                                                  ON_T4

SICK                                                                      SICK

ANTITHYROID                                                                                                     ANTITHYROID

Sex = male                                                             Sex = male

TSH = high                                                             TSH = high

TSH_BORD = high                                                TSH_BORD = high

T3 = normal                                                                                                             T3 = normal

T3_BORD = low                                                                                                     T3_BORD = low

                                                                                T3 = missing                            NOT(T3 = missing)

                                                                                T3_BORD = missing               NOT(T3_BORD = missing)

FTI = high                                                                FTI = high

FTI_BORD = high                                                   FTI_BORD = high

After that, the new rule will be added under the rule trace with at least one of the conditions selected by the expert from the difference list.

2.2 Lack of explicit domain knowledge in the RDR approach.

The current RDR approach does not include the possibility to supply an explicit model of the domain terms the expert employs, their relationships and abstraction hierarchies. As a result, some very important problems may emerge in these systems with respect to this lack of a shared understanding. To express this in precise terms, it can be said that RDR-based systems limit the potential for re-use and sharing as well as inter-operability. Also, in general, RDR leads to poor communication among different experts on the same domain. As a consequence, various assumptions and viewpoints concerning what is essentially the same subject matter can coexist. Thus, it is frequent that two different experts on the same domain employ different jargons. Moreover, each can possess differing (and possibly mis-matched) concepts and structures. In other words, conceptual and terminological confusion due to the non-presence of a shared understanding and communication among people who generally possess different perspectives of the domain (in accordance with their psychological characteristics, background knowledge, level of experience, etc.) may occur.

To overcome this problem, in this article we propose to extend the RDR approach with ontologies. The notion of ontology has become popular in research on knowledge engineering (Albert, 1993; Schreiber, 1993; Gruber, 1994; Guarino and Giaretta, 1995; van Heijst, Schreiber and Wielinga,1997). There is no commonly agreed definition of an ontology, but one that is more or less accepted is to define it as an explicit knowledge-level specification of a conceptualisation. In this paper, we adopt this definition, and view an ontology as the conjunction of a vocabulary describing domain elements along with the restrictions between the elements, for example Ø parent(x, x). In other words, an ontology constrains the structure and contents of domain knowledge. Domain knowledge, on the other hand, provides descriptions about factual situations in a certain domain.

In this work we will extend RDR-based systems with an ontological framework adapted to the particularities underlying these systems. In this sense, some research addressing how to extract ontological vocabulary in order to facilitate reuse has been performed (Richards, Chellen, Compton, 1996; Richards and Compton, 1997a; 1997b). These authors have made use of Machine Learning techniques and Formal Concept Analysis (Wille, 1982) to conceptualise domain knowledge present in the KB. Despite the fact that these techniques have demonstrated a good effectiveness, we think that, in general, the mental processes (e.g., abstraction, identification, etc.) necessary for constructing an ontological model from the domain knowledge are better performed by human beings. Moreover, experts should be the most appropriate agents to accomplish such processes, as they provide the domain knowledge

Our approach, which will be proposed in details further in this article, works from a new perspective in that the ontological vocabulary and relationships among terms must be provided, or exploited if the current ontological model is sufficient, by experts themselves whenever they wish to enter a new rule (and a new cornerstone case) to the system. In other words, the RDR philosophy about the construction of the domain knowledge will be extended to the construction of domain knowledge ontological models. We will attempt to design an ergonomic framework that integrates verification and consistence checking between the domain knowledge and the ontological model while the experts construct such a model.

3 DOMAIN KNOWLEDGE ONTOLOGIES FOR RIPPLE-DOWN RULES

3.1 Towards "ergonomic" knowledge structures for RDR-based systems

Independently of the knowledge representation schema adopted, it is very important to comprehend without great effort the structures underlying a KBS. In relation to this, there are a number of factors associated to knowledge structures that have an influence on the end-users’ comfort with respect to the system. Among these factors, Gaines (1995) has highlighted three as having a stronger influence on users’ preferences. These are the proximity of the terms used to the ones present in end-users’ normal language (i.e., their jargon), the structure size, and the structure form. Moreover, according to Sowa (1984), the reactions to what people see depend on their level of expertise. With all, it can be said that there exists no explicit rule that can be used to measure the comprehensibility of a KBS. There is, however, some consensus that conceptual hierarchies seem to be the most comfortable ones for non-programmers. Moreover, according to Gaines (1995), this type of structures can represent a notable contribution for systematising knowledge if one examines what has been published in this field until now.

3.2 Designing ontological operators for ripple-down rules-based systems

In this section, a set of ontological operators are defined so that they can be derived while experts enter the knowledge underlying ripple-down rules (together with their cornerstone cases) by means of conceptual hierarchies. The basic idea is that knowledge engineer applies the knowledge functions to the fragments of text, and the expert validates the so-obtained domain knowledge. So, this approach cannot be applied to RDR, where the KA process is performed only by the experts. The ontological operators are based on previous work on formally comparing knowledge elicitation techniques (Martínez-Béjar, Benjamins, Martín-Rubio, Castillo, 1996) and on a formal framework to analyse fragments of text using so-called "knowledge functions" (Martínez-Béjar, 1997; Martínez-Béjar and Martín-Rubio, 1997). We showed in (Martínez-Béjar, Benjamins and Martín-Rubio, 1997) how knowledge functions can be used as ontological operators that act on domain knowledge. In this paper, we will only describe the relevant operators for the concepts explained further in this article.

EXT operator Let Kru be the set of possible ripple-down rules and let Kc be the set of semantically different concepts underlying Kru. The extractor operator, written EXT, is defined as a function which maps Kru to Kc in order to obtain the semantically different concepts underlying a ripple-down rule.

ASC operator Given a hierarchy of concepts entered by an expert, the Ascendant operator, written ASC, is defined as a function which maps Kc to itself in order to obtain the parent concept of a concept obtained after applying the EXT operator to a particular ripple-down rule. Both concepts have been obtained by applying the EXT operator.

PRO operator Let Kp be the set of properties relative to Kc. The Properties operator, written PRO, is defined as a function which maps the Cartesian product Kru x Kc to Kp in order to obtain for each concept the set of properties involved in a particular ripple-down rule from which that concept has been obtained (i.e., after having applied the EXT operator to that rule). For example, by assuming that r is a ripple-down rule, and z is a concept belonging to EXT(r), PRO (r, z) provides the set of properties, which have to do with z, implicitly or explicitly referenced in r. In order to solve possible ambiguity problems, each of the so obtained properties can be written as concept.property, where property = PRO (r, z) and concept = z.

Based on these operators, the system can calculate a number of other cumulative parameters than can be used, for example, to guarantee that end-users do not repeat any term while they construct the conceptual hierarchy, since we make use of a Sets Theory-based representation. This extension is composed by a set of parameters, including the following:

MEXT operator Let R be a non-empty set of ripple-down rules. The multiple extraction operator, written MEXT, is defined as follows:

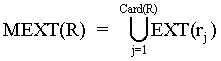
where rj stands for the jth ripple-down rule belonging to R.

With the operators mentioned above, we can extract various types of knowledge entities present in the domain knowledge (represented by means of ripple-down rules) put into the system by experts. However, a set of ontological operators would be more robust if PART-OF relationships could also be present in conceptual hierarchies. This is the reason why the relationships between concepts and sub-concepts are supposed to be either IS-A relationships or PART-OF relationships. The PART-OF relation is the study object of the Classical Mereology (CM), which is the formal theory about the concepts part, overlap and sum (see also Simons, 1987; Borst and Akkermans, 1997). Moreover, Eschenbach and Heydrich (1995) have argued that using CM in analysing different domains can help to know more about these domains. They have shown that CM is applicable to three different restricted domains provided that these are embedded in a less restricted domain. In this work, a restricted domain (which can be said to be embedded in that of Leonard and Goddman (1940)) has been defined. This domain will be referred to as a hierarchical restricted domain (HRD). By considering the precedent MEXT definition and that in an RDR-based system knowledge is incrementally added, the following definition can be done:

PHRD(t) Let R(t) be a non-empty set of ripple-down rules considered at the instant t; let MEXT be the multiple extraction operator; and let H be a hierarchical restricted domain. H is said to be a partial hierarchical restricted domain until the instant t, written PHRD(t), if it is defined as the set MEXT(R(t)).

Based on this, we will present new ontological operators (which are not knowledge operators).

M-parent operator Let c_i be a concept belonging to a non-empty PHRD(t) such that c_i is a proper part of another concept c_j. The mereological parent of c_i, written M-parent(c_i), is defined as the concept c_j.

where cj stands for the jth concept belonging to C.

Children operator Let c_i be a concept belonging to a non-empty PHRD(t). The set of children concepts of c_i, written children(c_i), is defined as {c_k Î PHRD(t) such that ASC(c_k) = c_i}.

PPRO operator Let R(t) be a non-empty set of ripple-down rules analysed until the instant t; let PRO be the property operator; and let c_j be a concept belonging to the PHRD(t) associated to R(t). The partial property operator until the instant t, written PPRO, is defined as follows:

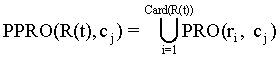
where r_i stands for the ith ripple-down rule belonging to R(t).

INH operator Let c_i and c_j be two different concepts belonging to a non-empty PHRD(t) such that either c_j = ASC(c_i) or c_i = PART-OF(c_j). The set of inherited attributes until the instant t, written INH(R(t),c_i), is defined as follows:

SPE operator Let c_i be a concept belonging to a non-empty PHRD(t). The set of specific attributes until the instant t, written SPE(R(t),c_i), is defined as the set PPRO(R(t), c_i).

ATT operator Let c_i be a concept belonging to a non-empty PHRD(t). The set of attributes for c_i until the instant t, written ATT(R(t), c_i) is defined as the union set INH(R(t),c_i) È SPE(R(t),c_i).

degree_of_overlapping operator Let c_i and c_j be two different concepts belonging to a PHRD(t). The degree of overlapping between c_i and c_j in the context of R(t), written degree_of_overlapping(R(t),c_i,c_j), is defined as the intersection set ATT(R(t), c_i) Ç ATT(R(t), c_j)

M-product operator Let C be a non-empty sub-set of concepts belonging to R(t). The mereological product of C with respect to R(t), written M-product (R(t),C), is

defined as the intersection set 

where c_k stands for the kth concept belonging to C

Until now, we have presented a set of operators to extract domain knowledge ontologies based on a combination of the operators defined earlier and Mereology. Now we will propose several formal properties useful for verifying the ontology (e.g., its consistency). A valid ontology has to satisfy all properties. These properties are especially important when the expert decides to rename existing knowledge entities (e.g. attributes) in taxonomic organisations. Non-fulfilment of a property means that a rename operation has (unforeseen) side effects that need to be taken care of. The following properties can be established.

PROP1 For every concept c_i in a PHRD(t), the following holds:

SPE(R(t), c_i) Ç INH(R(t), c_i) = f

In words, given a non-root concept, the intersection of its inherited and specific attributes is empty.

PROP2 For every pair of concepts c_i ¹ c_j Î PHRD(t) for which there exist two different concepts c₁, c₂ Î PHRD(t) defined as c₁ = ASC(c_i) and c₂ = ASC(c_j), respectively, the following holds:

degree_of_overlapping(R(t),c_i,c_j) > 0

Thus, concepts belonging to the same taxonomic sub-tree always have attributes in common.

PROP3 For every non-root concept c_i in a PHRD(t), the following holds:

INH(R(t), c_j) Í ATT(R(t), anc(c_i)), where

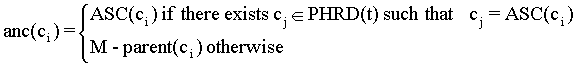
Thus, for every non-root concept, inherited attributes are also attributes of the parent concept.

PROP4 For every concept c_i in a PHRD(t) for which children(c_i) ¹ f , the following holds:

[Card(children(c_i)) ³ 2] ® [M-product(R(t), children(c_i)) Í ATT(R(t), c_i)]

In words, sibling concepts have the attributes of the parent in common.

PROP5 For every pair of concepts c_i ¹ c_k Î PHRD(t) for which children(c_i) ¹ f and children(c_k) ¹ f , the following holds:

Suppose that an expert wishes to create an RDR system from the following pair of ripple-down rules (expressed in natural language) R(ti) = {"If the vegetation is very short, there is only one stratum and the seasonal variation is medium, then the area under study has got a low visual fragility (VF)", "If there exists a predominance of pine merged with stone outcrops then the area under study has got a high visual quality (VQ)"} = {r₁, r₂}, and that he or she establishes the following conceptual hierarchy in two steps (corresponding to each rule):

Step 1 (for {r₁})

vegetation_landuse (VF) <---------- PART-OF -------- natural_vegetation (height, number_of_strata,seasonal_variation)

Step 2 (for {r₁, r₂ })

vegetation_landuse (VF, VQ) <------ PART-OF -------- natural_vegetation (height, number_of_strata,

seasonal_variation)<------ IS-A -------- pine (merging_with_stone_outcrops, predominance)

where

the information into brackets after each concept stands for the properties associated to it.

1. Based on this, the system can calculate PHRD(R(ti)) as follows:

PHRD(R(ti)) = MEXT(R(ti)) = EXT(r₁) È EXT(r₂) = {natural_vegetation, vegetation_landuse} È {pine, vegetation_landuse} = {pine, natural_vegetation, vegetation_landuse}.

 

2. The M-parent and the ASC operators are applied to the elements of PHRD(R(ti)):

 

ASC(pine) = {natural_vegetation};

M-parent(natural_vegetation) = {vegetation_landuse};

M-parent(vegetation_landuse) = ASC(vegetation_landuse) = f .

 

3. By considering the above steps and the definition of the children operator, the following is obtained:

 

children(pine) = f ;

children(natural_vegetation) = {pine};

children (vegetation_landuse) = f .

This means that the preconditions for PROP5 do not hold and, hence, PROP5 cannot be tested.

 

4. Then, the PRO operator is applied to each concept of each ripple-down rule:

PRO(r₁,natural_vegetation) = {height, number_of_strata, seasonal_variation};

PRO(r₁, vegetation_landuse) = {VF};

PRO(r₂,pine) = {merging_with_stone_outcrops, predominance};

PRO(r₂,vegetation_landuse) = {VQ};

 

5. By taking into account step 4, the following can be obtained:

 

SPE(R(t_i), pine) = PPRO(R(t_i), pine) = PRO(r₂, pine) ={merging_with_stone_outcrops, predominance};

SPE(R(t_i),natural_vegetation) = PPRO(R(t_i),natural_vegetation) = PRO(r₁,natural_vegetation) = {height, number_of_strata, seasonal_variation};

SPE(R(t_i), vegetation_landuse) = PPRO(R(t_i),vegetation_landuse) = {VF, VQ}

 

6. By using the INH operator, the following is obtained:

 

INH(R(t_i),vegetation_landuse) = f ;

INH(R(t_i),natural_vegetation) = f ;

INH(R(t_i),pine) = {height, number_of_strata, seasonal_variation}

 

7. If the ATT operator is now applied to the results obtained for the moment, the following can be derived:

1. By applying PROP1, we get the following:

 

SPE(R(t_i), vegetation_landuse) Ç INH(R(t_i), vegetation_landuse) = f ;

SPE(R(t_i), natural_vegetation) Ç INH(R(t_i), natural_vegetation) = f ;

SPE(R(t_i), pine) Ç INH(R(t_i), pine) = f ;

and, hence, PROP1 holds.

 

2. If PROP2 is now applied, the following can be obtained:

 

degree_of_overlapping(R(t_i), natural_vegetation, pine) = 3;

and, hence, PROP2 also holds.

 

3. By applying PROP3, the following can be written:

 

INH(R(t_i),natural_vegetation) = f ;

ATT(R(t_i), M-parent(natural_vegetation)) = ATT(R(t_i), vegetation_landuse) = {VF, VQ};

So, INH(R(t_i),natural_vegetation) Ì ATT(R(t_i), M-parent(natural_vegetation));

 

INH(R(t_i),pine) = {height, number_of_strata, seasonal_variation};

ATT(R(t_i), ASC(pine)) = ATT(R(t_i), natural_vegetation)) = {height, number_of_strata, seasonal_variation}.

So, INH(R(t_i), pine) = ATT(R(t_i), ASC(pine)) and, hence, PROP3 holds.

 

4. PROP4 cannot be applied in this case, since Card(children(c_i)) < 2 " c_i Î PHRD(t), i = 1,..,3.

 

5. PROP5 cannot not be applied because its preconditions do not hold (see step 3 above).

In conclusion, we see that the domain knowledge ontology satisfies all properties for which the preconditions hold.

4 RDR-ORIENTED CONCEPTUAL HIERARCHIES (ROCHs)

It should be noticed that RDR-based systems restrict both the number and the way in which modifications must be carried out in their associated conceptual hierarchies in order to ensure consistency among them. To be precise, it must be considered that RDR-based systems are constructed incrementally by adding domain knowledge and by impeding modifications or removing of knowledge already present in the KB. Thus, if one wants to modify some knowledge underlying the conceptual hierarchy, which reflects the ontological vocabulary and the relationships among terms, some restrictions must be defined in order to preserve the consistence with the domain knowledge present in the KB. This includes semantic as well as topological modifications of the structure of the conceptual hierarchy. In this Section, all possible operations on conceptual hierarchies constructed for an RDR-based system are analysed in detail in order to obtain the policy to follow when maintaining conceptual hierarchies.

4.1 Protocol for adding knowledge

To add knowledge to a particular conceptual hierarchy can consist of either adding new concepts or adding new attributes to existent concepts in the hierarchy. Each possible situation will be analysed in the following.

Adding a new concept Obviously, adding a new concept will have no influence on an RDR- based system since it does not contain any rule alluding that concept yet.

Adding attributes to existent concepts Although adding attributes to a particular concept means, in fact, to modify that concept, there will be no effect on the RDR-based system, as the new attributes are not referenced anywhere in the current system yet.

4.2 Protocol for modifying knowledge

To modify knowledge in a given conceptual hierarchy can mean either changing relations between concepts or modifying attributes. These possible operations will be analysed in the next subsections.

Modifying relations among concepts In general, to modify the relation between two concepts consists of moving the topologic position of a sub-tree having the root concept C_ik so that it is moved to be linked to the concept Cj.

The ontological reason for modifying relations among concepts is that when an expert is maintaining the conceptual hierarchy at the instant t in the context of an RDR-based system, written R(t), he or she can find another more suitable parent concept (i.e., an ascendant concept with more attributes in common) for the concept under question. In a formal way, and by using the above notation, the position change of the concept Cik in the hierarchy will take place only if Card(ATT( R(t), C_ik) Ç ATT( R(t), Cj)) > Card(ATT( R(t), C_ik) Ç ATT( R(t), C_{i -1})).

As the current RDR-based system can possess rules including attributes of any of the concepts in ST, and since RDR does not allow removal or modification of rules, those attributes will remain after the topological moving. Besides, the attributes belonging to the new parent of ST will be down inherited. Formally, the following will hold:

[ATT(R(t), C_ik)]after = [ATT(R(t), C_ik)]before Ç ATT(R(t), Cj)

where

 [ATT(R(t), C_ik)]after(before) represents the set of attributes linked to C_ik after(before) C_ik being moved;
ATT(R(t), Cj) is the set of attributes linked to Cj.

Modifying attributes To modify a particular attribute means to modify its range of possible values. Since there can be rules where that attribute is referenced, its modification will only be feasible if the new range is consistent with that of the same attribute belonging to the parent concept, if any, as well as with that of the set of descendants. Formally, it can be expressed in the following manner:

Let k Î N be the conceptual hierarchy depth considered in relation to an RDR-based system at the instant t, written R(t), let C_i, i = 1,2,..,k, be a concept of that hierarchy having a depth equals to i, and let range(ATT(R(t),C_i)) and newrange(ATT(R(t),C_i)) be the current values range of ATT(R(t),C_i) and the new values range to be assigned to ATT(R(t),C_i), respectively. Then, the modification of ATT(R(t),C_i) will be plausible only if one of the following conditions holds:

Although removing concepts from conceptual hierarchies might be feasible, we think that concepts should be kept there even if some of them are not used yet. The raison for adopting this policy is that further expert considerations can change in such a way that previously irrelevant concepts can become relevant for the system. In other words, these concepts could be incorporated as underlying knowledge in the RDR-based system related to the conceptual hierarchy under question.

The removing operations considered here include those of removing attributes and those of deleting possible values for particular attributes. The next subsections analyse these questions.

Removing attributes If some attributes are not used at all in the rules composing an RDR-based system, experts can be interested in removing them from the current conceptual hierarchy. This should be done carefully as there can be consistency problems as far as some non-referenced attributes in a concept by any rule in the RDR-based system may be referenced in sub-concepts underlying some rule in the RDR-based system. To avoid this inconvenience, the deleting process must be done by following a bottom-up strategy. In particular, this process will stop when a concept containing the attribute under question is found to be explicitly referenced in some rule in the RDR-based system.

Formally, to remove an attribute from a concept, the following must be carried out by the system here proposed:

Let k Î N be the conceptual hierarchy depth, let STi, i = 0,1,..,k, be a sub-tree of that hierarchy such that Ci is its root concept, and let att be the attribute to be removed from Ci. Then, att will be removed from Ci only if some of the following conditions hold:

In a formal way, the condition for some potential value, V, attached to a given context, written con, to be deleted is as follows:

Definition: ROCH Let H be a conceptual hierarchy obtained at the instant t and containing two concepts at least. H is said to be an RDR-oriented conceptual hierarchy, written ROCH, if the following conditions hold:

• it is a PHRD(t);
• there exists an RDR-based system associated to H so that all the concepts and attributes included in the RDR-based system (with their corresponding values ranges) are present in H;
• H is consistent with its associated RDR-based system, that is, PROP1, PROP2, PROP3, PROP4 and PROP5 (see Section 3) hold;
• Adding, modifying and removing knowledge operations in H can solely be performed according to the protocols established in this section.

5 IMPLEMENTATION OF ROCH-BASED SYSTEMS

According to the protocols (put forward in Section 4) for using ROCHs, a system, which we have called ROCH-Based System, written ROCH-BS, has been designed and implemented. This system consists of three modules, whose description is briefly exposed in the following lines.

XRDR can be said to be a simple, concise pre-existent implementation for single classification ripple-down rules. Initially conceived as an RDR tool, this module may be characterised as portable, flexible and easy to manipulate. The information to be provided to the system is exclusively composed by rule conditions, rule satisfaction branch, rule not-satisfaction branch, conclusion and cornerstone case. This simplicity makes XRDR a useful check-point for developing new techniques as well as for fast prototyping. Moreover, such a tool is helpful to do experiments. The fact that this tool has been employed for various simulation experiments (Compton, Preston, Kang and Yip, 1994; Compton, Preston and Kang, 1995) confirms its effectiveness.

The conceptual hierarchy module, that is ROCH, can be defined as a module which is assembled to XRDR through the Windows shell in such a way that end-users can, for example, add concepts to the hierarchy that they had created, assign relationships among concepts, add attributes to concepts, etc. Moreover, every non-root concept automatically inherits the attributes of its parent concept if the relation among them is a IS-A one. In addition to this, the attributes linked to every concept as well as their value ranges are visually accessible for end-users.

The DKO module, which is an abbreviation of Domain Knowledge Ontology, is in charge of creating and verifying the ontological vocabulary and the structure of the domain knowledge under question as experts enter knowledge to the system. This module is constructed by following the protocols stated in Section 4. Moreover, end-users interact with the system through a ROCH, which they can either create or edit (if it had been created already in precedent sessions). From the information in the hierarchy and the RDR system, ontologies are created and verified automatically. Furthermore, the representation complexity of the system can be calculated every time a new rule is entered through the conceptual hierarchy. Moreover, attributes can be removed at any time in accordance with a series of protocols. If so, the DKO module will verify that the consistence of the system is kept.

Although ROCHs can only be used by observing the protocols pointed out in previous Section, end-users can construct sets of attributes and values for a further assembling in a case. In this manner, when a case is assembled and it is complete (from the end-users’ point of view), it is sent to the XRDR part, where it is processed in order to provide the user with a conclusion. At this point, if user is maintaining the system and he or she does not agree with the so-obtained conclusion, RDR standard methods can be utilised to correct the KB.

In Figure 1, one example of a ROCH-BS session applied to the landscape classification domain is shown.

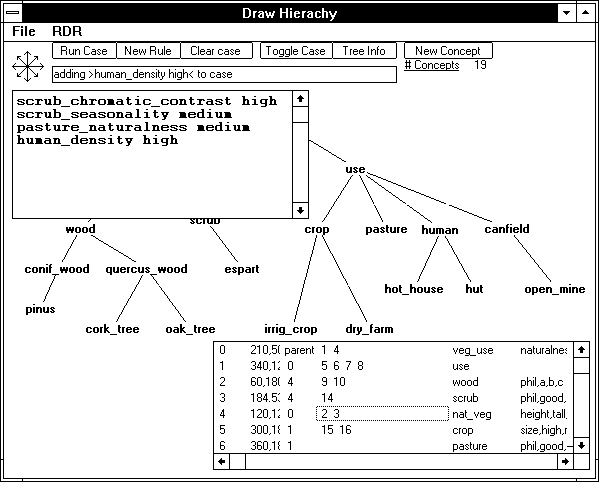
6 CONCLUSIONS

Ripple-down rules (RDR) can be viewed as a methodology for building knowledge-based systems where both the knowledge acquisition process and the maintenance one are performed by the domain experts. In other words, the presence of any knowledge engineer is not necessary in such processes. However, this methodology has various applicability restrictions, including the type of task to be solved (only classification tasks), the kind of knowledge that can be contemplated by the system (only "if-then" rules) etc. With all, despite the fact that RDR has proven to be successful as a problem-solving method for certain type of domains, it fails to explicitly provide to end-users with both the structure and the vocabulary associated to the domain knowledge they are dealing with for a particular task. As a result, strong impediments for re-using and sharing domain knowledge in RDR-base systems arise.

On the other hand, reusable ontologies are increasingly being recognised as an important research area in the development of knowledge-bases systems. Their purpose is to supply mechanisms for constructing domain knowledge from reusable components. However, there are no standard universally-accepted methodologies to build ontologies due to the difficulties and costs involved in their construction processes. In this paper, we have presented a formal framework that allows to construct and verify domain knowledge ontologies for RDR-based systems. Besides, we have chosen a knowledge representation (i. e., conceptual hierarchies) that can be used as an operative interface mechanism between RDR-based systems and end-users when they construct cases and, eventually, rules. In this sense, with this new system, concepts and relations among them, in the context of a case, must be made explicit by experts in a conceptual hierarchy. Therefore, with this approach experts are in charge of two more tasks (in relation to the ones they must perform with classical RDR-based systems), namely, that of identifying concepts and that of identifying relations among them.

We are aware about the fact that it could be argued that this framework can be not so easy to manipulate by experts as traditional RDR-based systems. This stems from the requirement for performing more conceptualisation work in the new approach. However, we think that the plausibility of introducing more operative complexity in the new framework can be justified in some cases. To be precise, in the proposed framework, experts are assumed to be the most adequate agents in KBS development to carry out abstraction of knowledge (i. e., abstraction of concepts and their relationships) from other knowledge made explicit by themselves previously.

We have proposed a set of ontological operators that enable the structured extraction and verification of domain knowledge ontologies while experts enter knowledge (through conceptual hierarchies) to an RDR-based system. These operators are partially based on a reformulation of our previous works on mathematical knowledge functions (Martínez-Béjar, Benjamins, Martín-Rubio and Castillo, 1996; Martínez-Béjar and Martín-Rubio, 1997) complemented with mereological concepts (Martínez-Béjar, 1997; Martínez-Béjar, Benjamins and Martín-Rubio, 1997).

To illustrate the utility of these ontological operators, we have shown an example where a simple domain knowledge ontology is constructed and "verified" according to the verification possibilities that the formal framework here proposed offers. The domain knowledge involved in this example stems from a real problem consisting of a landscape classification task in Spain.

It can be said that our approach is concerned with the construction of ontologies starting from knowledge elicited from experts by themselves as they must, for example, establish relations between concepts in the underlying conceptual hierarchy. Therefore, the so-built ontologies can be viewed as application ontologies or domain ontologies, depending on whether the knowledge obtained is more or less general. From this point of view, the approach here presented is complementary to others that supply techniques and methods to configure ontologies from pre-existent ontologies. Thus, for example, the KACTUS approach (Schreiber, Wielinga and Jansweijer, 1995) and ONTOLINGUA (Gruber, 1993) respond to this schema.

The fact that in the approach proposed here, conceptual hierarchies are used to compound cases or rules for RDR-based systems, means that all the terms taking part of the domain knowledge, which is represented in RDR by means of "if then" rules, are reflected on such hierarchies. Hence, every time end-users modify the structure or the contents of conceptual hierarchies associated to an RDR-based system, inconsistencies among these two modules can be occasioned. To avoid this problem, a series of protocols for maintaining such hierarchies has been proposed. These protocols also take into account the particular characteristics of RDR, where removing or modifying domain knowledge is not allowed, that is, the domain knowledge growth is monotonic. In this paper, systems composed by an RDR-based system and a conceptual hierarchy holding the mentioned protocols and allowing to construct and verify domain knowledge ontologies (in the manner already indicated) have been termed ROCH-based systems.

Finally, a tool based on the characteristics of ROCH-based systems has been designed and implemented. Nowadays, this tool is being utilised by two different research groups in order to evaluate it for different problem domains. These groups belong to the Department of Computer Science of the University of Murcia (Spain) and the Department of Artificial Intelligence of the University of New South Wales (Australia), respectively. After the evaluation process, we plan to extend the prototype to other environmental planning tasks related to the landscape classification task.

REFERENCES