(1) 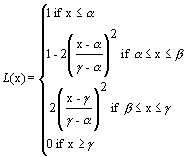
(2) 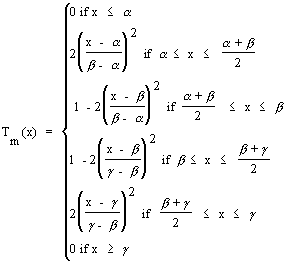
(3) 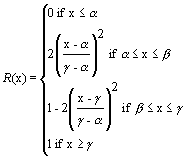
Where
b = (a + g )/2;
Using Ripple Down Rules-based Systems for Acquiring Fuzzy Domain Knowledge
Rodrigo Martínez-Béjar1, Hossein Shiraz2 and Paul Compton2
1 Spanish Scientific Research Council, Avda. La Fama, 1, C. P. 30080- Murcia, Spain. E-mail: rodrigo@pandora.dif.um.es
2
Department of Artificial Intelligence, School of Computer Science and Engineering, The University of New South Wales, Sydney, 2052 NSW, Australia. Email : {hossein,compton}@cse.unsw.edu.auAbstract
Fuzzy rule-based systems allow a more natural expression of concepts by experts and users than crisp systems. Although the use of fuzzy concepts partially reduces the maintenance problems it introduces other problems in tuning the numbers used by the system. On the other hand Ripple Down Rules provide easy maintenance but only for crisp concepts, albeit that the crisp concepts can be refined in local contexts. The aim of this paper was to develop a theoretical foundation for combining RDR and fuzzy rules to try to capture the advantages of both. We believe that advantages can be demonstrated, but a number of issues remain to be resolved.
Ripple down rules (RDR) is a knowledge acquisition technique developed from the maintenance experience with an expert system (Compton et al., 1989). The main motivation for developing RDR was the fact that experts could not explain how they had reached conclusions. Nevertheless, they were capable to justify the correction of the conclusions by attending to the context in which they had been provided (Compton and Jansen, 1990). RDR uniquely uses the knowledge provided by experts in the context it was provided, that is, by following the sequence of evaluated rules. Moreover, if the expert does not agree with a conclusion, knowledge in the form of a new rule can be added. In this sense, rules are never removed or corrected, only added.
Two main RDR-based approaches have been developed recently. Multiple Classification Ripple Down Rules (MCRDR) (Kang, 1996) is an extension of the basic aspects of RDR for providing multiple independent conclusions. With MCRDR, more general than those of single classification can, hence, be performed. When experts are maintaining a MCRDR system, they must construct a rule containing the differences between the case is entered to the system and the case associated to the last true rule in the KB. This process will be repeated until there is no case (associated to any rule) satisfying the rule.
A further RDR-based approach developed recently is the so-called Ripple down rule-Oriented Conceptual Hierarchy (ROCH) (Martínez-Béjar et al., 1997b). The basic idea concerning ROCH-based systems is that experts themselves can construct and validate domain knowledge while they enter knowledge to the KB. The purpose of this paper is to obtain a formal model to extend the knowledge acquisition/representation schema underlying current ROCH-based systems so that fuzzy domain knowledge can be acquired/represented. The aim is achieved by exploiting the characteristics of fuzzy domains in combination with the RDR philosophy. Thus, by introducing some assumptions, a model for acquiring knowledge in fuzzy contexts through RDR has been constructed. The ideas in this article will generally be illustrated with an existing KBS project for environmental planning in Spain.
The structure of the paper is as follows. Section 2 offers a description of the work done in RDR to-date. In Section 3, we offer a brief introduction to the concept of fuzzy logic and fuzzy expert systems. Also, a formal manner for modelling fuzzy modifiers as well as fuzzy frequency quantifiers is proposed. Section 4 provides a knowledge representation schema that allows to adapt ROCH-based systems to fuzzy domains. Section 5 shows how cases are constructed in our approach. In Section 6, we analyse the different situations that can arise when a case is run in the model presented. Section 7 proposes a mechanism partially based on some fuzzy logic properties to acquire/show conclusions. In Section 8, the process required to acquire rule conditions in the system is described. Finally, in Section 9 we present conclusions.
Ripple down rules (RDR) is a knowledge acquisition technique and expert system methodology that was developed as a result of maintaining a medical expert system, the GARVAN-ES1 (Compton et al., 1989). From a long maintenance experience with this system, it became clear that when experts were asked how they had reached a particular conclusion they did not and could not explain how they had reached their conclusion. Rather, they justified that the conclusion was correct, this justification being a function of the context in which it was provided (Compton and Jansen, 1990; Compton, 1992). The justification varied depending on whether the expert was trying to justify their conclusion to a fellow expert, a trainee, lay person or knowledge engineer, etc. This viewpoint on knowledge has much in common with situated cognition critiques of Artificial Intelligence and expert systems (Dreyfus and Dreyfus, 1988). These critiques do not necessarily lead to abandoning the expert system endeavour, but change the focus of development (Winograd and Flores, 1987; Clancey, 1991; Clancey, 1993). RDR is a practical realisation of, at least, part of these viewpoints.
The RDR approach produces a structure IF...ELSIF....ELSIF....ELSIF..., etc., that is, a decision list but with decisions refined by further decision lists (Catlett, 1992). Such a structure is also a decision tree, although it is normally very unbalanced, so that is better described in a decision list. The aim of RDR is to use the knowledge an expert provides only in the context within which it is provided. For rule based systems, it was assumed that the context was the sequence of rules which had been evaluated to give a certain conclusion. Thus, if the expert disagrees with this conclusion and wishes to change the knowledge base so that a different conclusion is reached, knowledge is added in the form of a new rule of whatever generality the expert requires. Moreover, this rule can only be evaluated after the same rules are evaluated with the same outcomes as before. With this approach, rules are never removed or corrected, only added. All rules provide a conclusion, but the final output of the system comes from the last rule that was satisfied by the data.
An essential part of any RDR system is the maintenance of cornerstone cases. These cases are cases that caused some change to the system. That is, they are cases, which caused the expert to create a new rule. For each rule in a system there is a cornerstone case. There are several reasons why these are important. Trivially they provide a history of the development of the system for documentation purposes. More importantly, they provide a context within which new rules can be created.
The initial RDR systems built are only single classification systems, where rules are linked in a binary tree structure and a single case is stored with each rule. To correct a conclusion, a new rule is appended at the end of the inference path through the tree that had produced the wrong conclusion. More formally, Scheffer (1996) has defined a single classification RDR by means of exception (true) rules and "if-not" (false) rules. By using this approach, the exception rules are evaluated once a rule is satisfied. If so, none of the if-not rules are tested. Single classification RDR has shown to be a successful approach in the development of the PEIRS system, which is a medical expert system used for pathology laboratory report interpretation. This system was built, whilst in routine use, by experts with no help of knowledge engineers (Edwards et al., 1993).
The basic philosophical background of RDR has been extended to provide multiple independent conclusions (MCRDR) (Kang and Compton, 1992). The same events occur in a MCRDR-based system as in a simple RDR-based one, but with the added requirement that rules may have multiple cornerstone cases, and these are associated with multiple conclusions (Kang et al., 1995; Kang, 1996). More formally, MCRDR can be defined as an n-array tree structure containing exception rules and siblings so that all of these, which are situated at the first level, are evaluated. Then, the list of children is also evaluated until all children from true parents have been examined. Thus, the conclusion for the case under question is formed by the last true rule of each pathway.
When experts maintain a MCRDR system, they work as follows. First, they are required to construct a rule containing the differences among one of the (existent) cornerstone cases and the input case. In order to exclude a further case when other stored cornerstone cases satisfy the rule, further conditions will be required to be added. This process will take place repeatedly until there is no stored cornerstone case satisfying the rule. This could lead to maintenance processes involving many cases to be checked for each new rule. However, Kang et al. (1995) have shown that after seeing a few cases (normally two or three), experts supply an adequate rule in terms of precision fundamentally. With all, Kang (1996) has demonstrated experimentally that knowledge bases produced by MCRDR systems are usually more compact and with less repetition than RDR. This author has indicated that such a phenomenon can be due to the fact that MCRDR systems focus more on exploiting experience rather than depending on the KBS structure.
More recently we have designed and implemented a framework, which has been termed Ripple down rule-Oriented Conceptual Hierarchy (ROCH)-based system (Martínez-Béjar et al., 1997b), that allows experts to construct and validate domain knowledge ontology while they enter knowledge to the KB for RDR-based systems. In essence, in ROCH-based systems, for every application domain, experts construct cases (and, eventually, enter rules and their corresponding cornerstone cases) by using a conceptual hierarchy, namely, ROCH, which is created and maintained by the experts themselves. Such a hierarchy includes both IS-A and PART-OF relationships and, although it must be established by the experts, it is verified by the system. For instance, consider the following example (extracted from Martínez-Béjar et al. 1997b).
Suppose that an expert wishes to create a RDR system from the following pair of ripple down rules (expressed in natural language) R(ti) = {"If the vegetation is very short, there is only one stratum and the seasonal variation is medium, then the area under study has got a low visual fragility (VF)", "If there exists a predominance of pine merged with stone outcrops then the area under study has got a high visual quality (VQ)"} = {r1, r2}. Let us also assume that there is no conceptualisation yet (as the expert wants to create a KB). Then, the expert would establish the following conceptual hierarchy in two steps (corresponding to each rule):
Step 1 (for {r1})
vegetation_landuse (VF)
PART-OF
natural_vegetation (height, number_of_strata,seasonal_variation)
Step 2 (for {r1, r2 })
vegetation_landuse (VF, VQ)
PART-OF
natural_vegetation (height, number_of_strata,seasonal_variation)
IS-A
pine (merging_with_stone_outcrops, predominance)
where the information into brackets after each concept stands for the properties associated to it. At this point, after the system verifies that this conceptual hierarchy is consistent (for example, by ensuring that inheritance properties hold among their IS-A nodes), the system could compound the rules to be incorporated in the KB.
In short, the goal of this work is to extend the RDR approach applicability, so that a more variety of forms for expressing the domain knowledge can be addressed. In particular, the fundamental purpose here is to extend in a step-by-step process the exclusive, restrictive model of knowledge acquisition/representation contemplated in ROCH-based systems (that is, the classical "if ..then" rule with crisp values) to deal with fuzzy domains in a more natural manner from the experts' view.
In this paper, we will make use of some basic concepts used in fuzzy logic that allow to address the problem of how to represent knowledge underlying fuzzy domains. However, although our work is not intended to be situated in the approximated reasoning field, some particular characteristics of the RDR philosophy (e. g., that experts are in charge of performing the KA process) should be taken into account when acquiring/representing this kind of knowledge.
Fuzzy logic, which has widely been used for representing imprecise knowledge in expert systems (Baldwin and Pilsworth, 1980; Zadeh, 1983; Yager, 1984; Sugeno, 1985; Kandel, 1990; Lopez-De mantaras, 1990; Watanabe, 1991; Baldwin, 1992; Grabot et al., 1994), is basically a method to allow a gradual representation of likeness between two objects. It is based on the theory of fuzzy sets (Zadeh, 1965), which defines a membership function to assign a grade of membership between 0 and 1 to each element in the range of all possible elements under consideration. This grade can be thought as a measure of compatibility between the element and the concept represented by the fuzzy set. Formally, the membership function for a fuzzy set A, written
m A(x), is a real valued function defined as the application m A: X ® [0,1] for all x in a universal set X.Fuzzy sets are used to model the vagueness and imprecision present in natural language. Thus, they can be employed to represent concepts such as rarely and often. These terms are usually known as linguistic quantifiers and are very common in natural language. The amount of vagueness can be regulated by means of the so-called modifiers or hedges, which act in combination with linguistic quantifiers. Examples of modifiers are more and very.
In order to make different applications possible, several kinds of inference should be allowed. In this sense, in this work the Generalised Modus Ponens (GMP) approach, which has been used by some successful expert systems (see, for example, Hwang (1995) or Gisolfi and Di Lascio (1995)) has been chosen. Such an approach provides a framework where different types of inference semantics can be supported.
Through the GMP technique, the proposition y is B can be derived from the rule "if (x is A) then (y is B)" when the proposition x is A is true. The GMP can also be employed when the two propositions x is A and y is B are defined imprecisely. Thus, if a proposition x is A’, close to x is A, is true, the principle of the GMP is to derive another proposition, written y is B’. This proposition is generated by taking into account both the underlying semantics of the implication of the rule and a measure of the likeness between A and A’. With all, the inference consists of defining a fuzzy set B’ which is as close to B as A’ is to A. More formally, Dubois and Prade (1988) have computed the membership function of B’, written
m B’, as follows:"
y Î Y, m B’(y) = supx Î X T(m A’(x), (x ® y))where
Y is the referential of y;
X is the referential of x;
T is a triangular norm that makes the GMP compatible with the classical modus ponens;
m
A’ is the membership function of A’; and(x
® y) represents an implication denoting the kind of causal link involved in the production rule.According to Buckley et al. (1986), a fuzzy expert system (FES) must hold the following :
More formally, every FES can be characterised by the following:
A number of FESs have been successfully implemented to-date. Examples of these can be found in Adlassnig et al. (1985), Binaghi et al. (1993), Fathi-Torbaghan and Meyer (1994), Gisolfi and Di Lascio (1995), Hwang (1995), Daniels et al (1997) and Martínez-Béjar et al. (1997a). Some of the quoted systems use gausssian models for defining membership functions (Zadeh, 1983). These are particularly interesting when the usual values given to the fuzzy terms employed by experts can be represented by means of a triple (T) such as <low, medium, high>, <short, medium, high>, etc. We will term to each component of T as Tl, Tm, and Tr, respectively. Given a triple T, the formal definition of the mentioned functions is the following:
|
(1)
|
(2) |
|
(3) |
Where b = (a + g )/2;
|
For example, the fuzzy set dense_pineland can be represented by means of the functions Tl(x), Tm(X) and Tr(x) where
a = 70 and g = 90.Usually, the fuzzy terms to be modelled are adjectives, which can be preceded by fuzzy modifiers such as "very", "not", etc. This problem is addressed in the following example. Let us consider the sentence "the vegetation density is high" where the term "high" is represented by a continuous fuzzy function. Suppose now that the modifier "very" transforms "high" into another continuous fuzzy function so that sentences such as "the vegetation density is very high" are allowed by the system where the expression "the vegetation density" can take values from a fuzzy term denoted as "high". In this situation, the so-called TFM function (Kandel, 1990) has demonstrated to be useful (see, for example, Gisolfi and Di-Lascio (1995)). This function works as follows:
Let D be a fuzzy set, and let m be a truth modifier. Then, the result of modifying D by means of m, written TFM(D/m), is a fuzzy set, written mD, such as
m mD(x) = m m(D(x)) where the m S(V) function stands for the membership degree of the variable V with respect to the set S.A practical example of the use of that function is the one pointed out in Martínez-Béjar et al. (1997a). In this case, we have modelled the vague predicates containing modifiers by using the next TFM function:
(4)
m mD(x) = m m[ D(x)] dwhere
0 <
d
> 1 if the modifier m makes D to hold clearly. Examples are lot, very, much and extremely.Although, as it has been pointed out already, in this paper ROCH-based systems are used instead of classical RDR, problems still remain if one wants to apply the RDR philosophy to fuzzy domains. Firstly, ROCH-based systems can only operate with crisp values for the attributes in their rules. Nevertheless, fuzzy domains are typically concerned with rules following the next format:
IF (X 1 is V 1) and (X 2 is V 2) and .....and (X n is V n) then Y is A
where
X i stands for the ith variable (i.e., the ith attribute associated to a particular concept) to be taken into account; i = 1, 2, .., n;
n = number of sub-conditions present in the rule under question;
V i represent the value associated to X i . This can be either a crisp value or a fuzzy function;
Y stands for the variable associated to the conclusion of the rule;
A represents the value associated to Y. This value can be either a crisp value or a fuzzy function.
It could be argued that a "fuzzy" ripple down rule can always be substituted by a set of "crisp" ripple down rules. However, in general, using imprecise rules for describing situations very close each other allows to represent the underlying knowledge in a more adequate, efficient way (Grabot and Caillaud, 1996). For instance, let us consider the problem of inferring the possible landscape visual quality from the vegetation diversity that such landscape presents. This expertise could be described in a discrete way through a set of rules as follows:
R1: If (vegetation.diversity = 10) then (landscape.visual_quality = 5%);
R2: If (vegetation.diversity = 20) then (landscape.visual_quality = 22%);
...
Rn: If (vegetation.diversity = 10.000) then (landscape.visual_quality = 100%).
If knowledge is represented in this manner, the influence of other factors, for example vegetation density, can result in a variation of the landscape visual quality. Hence, the connection between the antecedent and the conclusion is eventually less evident than that present in an imprecise rule. In addition to this, it should be noticed that to cover the variation field of the vegetation diversity, a number of rules would be necessary.
Another way of expressing that experience could be the following:
R1: If (vegetation.diversity < 10) then (landscape.visual_quality < 5%);
R2: If (10 < vegetation.diversity < 20) then (6% < landscape.visual_quality < 22%);
...
Rn: If (vegetation.diversity > 9.999) then (landscape.visual_quality = 100%).
Notice that this way to describe the expertise involves imprecision, since it employs intervals rather than precise values. Besides, this approach introduces subjective threshold, so that it is necessary to have many arbitrary thresholds to obtain a good precision. On the contrary, fuzzy logic allows to represent this knowledge by means of a unique rule and, hence, to reduce the negative effect of the use of arbitrary thresholds. For example, such a rule could be "if (vegetation.diversity is high) then (landscape.visual_quality is high)".
Although, as it has already been pointed out, the research topics addressed in this work are intended to be far from those of fuzzy logic or fuzzy sets, most existent approaches to fuzzy modifiers/quantifiers have been conceived to allow for automated fuzzy reasoning in the systems where they have been applied (Baldwin and Pilsworth, 1980; Adlassing and Kolarz, 1982; Kandel, 1990; Lopez-De Mantaras, 1990; Gisolfi and Di-Lascio, 1995; Grabot and Caillaud, 1996; Daniels et al., 1997). Thus, in these approaches modifiers/quantifiers are modelled by the system itself.
However, we think that in RDR the experts must be in charge of such a task according to their particular criteria, the system being only concerned with guaranteeing consistency. This has been the foundation for proposing an expert-driven policy for modelling fuzzy modifiers and fuzzy frequency quantifiers.
With all, a model, which can be used not only for ROCH-based systems, to manipulate fuzzy modifiers and fuzzy frequency quantifiers is formally formulated in the following lines.
3.3.1 Modelling of fuzzy modifiers
As it has been pointed out in Section 3.1, fuzzy attributes may be preceded by fuzzy modifiers, to which the TFM function (Kandel, 1990) can be applied. However, there are many different linguistic modifiers that could potentially be used by the experts when they create or maintain the system. In this sense, fuzzy modifiers used by experts independently of the application domain can be considered. Moreover, they can be grouped into several sets attending to their modification intensity. For instance, a possible fuzzy modifiers classification, which will be considered further in this work, is the following:
a) "Positive" sets of modifiers
RADICAL_POSITIVES = P1 = {"completely", "extremely", "radically", "absolutely", "totally",..};
MODERATE_POSITIVES = P2 = {"very", "much", "lot", "quite",..};
b)"Negative" sets of modifiers
RADICAL_NEGATIVES = N1 = {"almost nothing", "hardly",.. };
MODERATE_NEGATIVES = N2 = {"little", "bit", "few", "more or less", "almost",..};
c)Set of "is-not" forms
IS_NOT = {"not", "not at all", "nothing" "completely not", "practically not", "absolutely not", "practically nothing",..}.
Once the possible modifiers to be used have been classified into sets, experts can be shown all these sets into which they can include the modifiers, if any, when they construct cases or rules through a ROCH.
On the other hand, it can be noticed that the modifiers belonging to Ni (Pi) are more intense that those belonging to Nj (Pj) if i < j; i, j = 1, 2. By taking this into account and by employing the TFM function used in Section 3.1, if it is assumed that fuzzy modifiers act on any of the elements of the triple < Tl(x), Tm(x), Tr(x)>, the following modelling criterion has been adopted.
Let
m mT(5)
m mT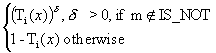
In order to give an appropriate value to the parameter
d , it must be taken into account that all the elements included in the negative sets of modifiers affect Ti(x) in a different manner as those included in the positive ones. In particular, and by considering the equations defining Ti(x), if the modifier belongs to any of the negative sets of modifiers, the values for d should imply a greater membership function than Ti(x). Similarly, if the modifier belongs to any of the positive sets of modifiers, the values for d should imply a less membership function than Ti(x).With all,
d can be defined as follows: (6)Where: (7) ![]() , i
, i
For example, if we consider the above sets of modifiers, (6) can be applied with np = nn = 2 and, then,
d can be defined as follows:(7.1) ![]() , i
, i
3.3.2 Modelling of fuzzy frequency quantifiers
It should also be taken into account that there are linguistic fuzzy quantifiers referred to as frequency quantifiers, for example, always, seldom, etc. Hence, they have not been contemplated in any of the modifiers sets above defined. Moreover, fuzzy modifiers can be combined with the referred fuzzy modifiers in linguistic expressions, for example "A is seldom very high". Therefore, it is an interesting endeavour to attempt to model how these quantifiers act on a fuzzy attribute, which in turn, can be preceded by a fuzzy modifier. In this sense, and by reasoning as before for fuzzy modifiers, various sets integrating linguistic quantifiers according to their frequency intensity can be formed. A classification of such quantifiers is, for instance, the following:
HIGH_FREQUENCIES = H= {"almost always", "very often", "often",..}= {h1, h2, h3,..};
LOW_ FREQUENCIES = L = {"almost never", "very seldom", "seldom",..}= {l1, l2, l3,..};
FACTS = F = {"always"};
IMPOSIBLE_FACTS = I = {"never"}.
Notice that H and L can be disposed in such a way that they can become ordered sets (as, in fact, the above sets are) in the sense that hi produces more frequency that hj if i < j, while li produces less frequency that lj if i < j; i, j = 1,..,3. Moreover, a method to obtain representative numerical values for some linguistic quantifiers has been proposed by Adlassnig and Kolarz (1982), as Table 1 illustrates .
|
always 1.00 |
almost always 0.99 |
|
very often 0.90 |
often 0.75 |
|
seldom 0.25 |
very seldom 0.10 |
|
almost never 0.01 |
never 0.00 |
Table 1
. Representative numerical values for some linguistic quantifiers
However, it can be noticed that the values these authors propose are limited to the fuzzy quantifiers present in the table. Thus, if some new fuzzy quantifier is pretended to be added, several options can be adopted. Thus, the input fuzzy quantifier may be approximated to one of those contained in the table. Also, some other approximation that can generate a representative numerical value, which depends on the quantifier under question, can be considered.
In the case of ROCH-based systems, given that the experts are in charge of performing both the KA and the maintenance processes, they should have the possibility of choosing in which set amongst the above ones to insert the quantifiers, if any, when they enter cases or rules to the system. In addition to this, as it can be noted, representative numerical values for quantifiers in Table 1, depend on the intensity. With all, a mechanism to generate the values to be given to quantifiers can be defined. For it, it should also be taken into account that the size of the anterior quantifier sets must be considered in order to select the distances among these values. Such a mechanism is formally exposed in the following lines.
Let m qmT![]() (x) be the membership degree of the variable x with respect to the set qmTi, where m and Ti(x) are defined as before and the frequency factor, written q, belongs to the union set H È L È F È I, all of these sets being non-empty and finite. Then, m qmT
(x) be the membership degree of the variable x with respect to the set qmTi, where m and Ti(x) are defined as before and the frequency factor, written q, belongs to the union set H È L È F È I, all of these sets being non-empty and finite. Then, m qmT![]() (x) can be defined as follows:
(x) can be defined as follows:
(9) m qmT![]() (x) = qm mT
(x) = qm mT![]() (x) where
(x) where
(10)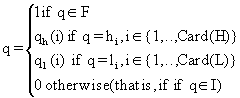
(11)![]() , CH = Card(H) + 2; (12)
, CH = Card(H) + 2; (12)![]() , CL = Card(L) + 2.
, CL = Card(L) + 2.
For instance, by using the sets of frequency quantifiers defined above, (10), (11) and (12) can be defined as follows:
(10.1) 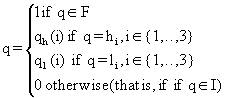
(11.1) ![]() (12.1)
(12.1) ![]()
By assuming that the membership functions for fuzzy attributes respond to the model of the triple <Tl(x), Tm(x),Tr(x)> as indicated earlier, and that experts can effectively be aware about the fact that they can represent their knowledge in this way, these attributes can be defined as a function of two different parameters, namely,
a and g (obviously, in addition to the linguistic terms that univocally identify that attribute). In so doing, we might also provide the experts with the possibility of defining these numbers with confidence intervals, as it frequently happens in real life. Moreover, the possible presence of modifiers or frequency quantifiers in their jargon can also be considered. With all, and by taking into account the notation employed until now, the next definition concerning the application of ripple down rules to fuzzy domains is proposed.Definition 1: FROCH-based system
Let R be a ROCH-based system. R is said to be a fuzzy ripple down rules-oriented conceptual hierarchies (FROCH)-based system, written FROCH-based system, if the rules can be applied to fuzzy domains by modelling fuzzy attributes, fuzzy modifiers and fuzzy quantifiers as it has been established in this Section, so that every valued attribute, written VA, is represented as follows:
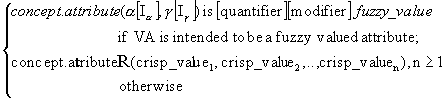
the elements into brackets standing for optional elements in the representation, that is, they can be present or not in the attribute structure, depending on whether the experts make use of them in the description of input cases, and where
concept stands for the identifier concept in the FROCH for which VA is valued;
attribute is the identifier employed for VA;
a
and g are the parameters necessary for defining three membership functions for VA according to the triple <Tl(x), Tm(x),Tr(x)>;I
a and Ig stand for the confidence intervals given by the expert for a and respectively, and holding that Ia , Ig Î (0, 50%);quantifier represents an element of the union set H
È L È F È I;modifier represents an element of the union set P
È N È IS_NOT;fuzzy_value represents a fuzzy value given to VA according to what any of functions in the triple <Tl(x), Tm(x),Tr(x)> represents , that is, high, medium, normal, low, short, tall, etc.
R represents a mathematical relationship, including equality, order and membership, among the underlying attribute (i.e., the VA) and the elements of the set{crisp_value1, crisp_value2,.., crisp_valuen};
crisp_valuei, represents the ith non-fuzzy value for VA, 1
£ i £ n.With RDR-based systems, the KA process is performed while the expert is maintaining the system, as it has been pointed out in Section 2. In addition, as MCRDR makes possible to have multiple independent conclusions, we will assume that the implicit problem-solving method in FROCH-based systems will be that of MCRDR. So, the KA process, will essentially be the same as that used in MCRDR. To be precise, by using FROCH-based systems, the KA process will consist of performing the following steps:
(S1) The expert builds an input case through the FROCH.
(S2) The system runs the input case, that is, this is confronted to the rules present in the KB.
(S3) The system shows the conclusions, if any, obtained (acquired) by the system for the input case in such a way that all rule traces are stored.
(S4) If the expert disagrees with some of these conclusions or is missing a conclusion (by assuming that no conclusion is the default), after inference, the system retrieves information regarding the cornerstone case associated to each rule that provided a wrong conclusion together with information about the input case. Then, the knowledge acquisition process will proceed as follows:
(S4.1) The system acquires the correct conclusions from the expert.
(S4.2) The system decides on the location of the rules to be entered by the expert.
(S4.3) The system acquires new rules from the expert and adds them in order to correct the KB.
Regarding the steps to be followed in the KA process in a FROCH-based system once an input case has been constructed from a FROCH, several issues should be addressed. Firstly, to accomplish the step (S1), that is, to construct an input case from a FROCH, a different mechanism from that of ROCH must be defined, since some conditions in the case could be fuzzy valued attributes. Secondly, a compatibility mechanism to confront an eventual fuzzy ripple down rule with a case that can be expressed by means of (some) fuzzy valued attribute must be provided. Furthermore, such a mechanism should also address the problem of defining the criteria to match a condition having the fuzzy valued attribute format against another condition which could not have such a format (i. e., it could be a crisp condition).
Thirdly, given the representation schema for fuzzy valued attributes adopted in this paper, to carry out the step (S3), the system must contemplate the possibility that several conclusions about the same valued attribute could be generated. In this case, the system must have a mechanism to help the expert to select a unique conclusion concerning the same fuzzy attribute, by taking into account all the possible candidate conclusions. Fourthly, if the input case or the cornerstone case implied in the addition of a new rule (see step (S4.3)) contains some fuzzy valued attribute, the way in which the system constructs difference lists must also consider all the parameters and elements involved in the representation for such attributes.
With all, the problems derived from the implications of using fuzzy valued attributes when performing the KA (as indicated above) with FROCH-based systems are analysed in the following Sections.
In addition to the possibilities that ROCHs offer to construct cases from a conceptual hierarchy, in FROCHs, the expert must have a way to account for the fuzzy values and the parameters defining an eventual fuzzy valued attribute when he or she is constructing an input case. Moreover, the experts can also have the necessity of considering fuzzy modifiers or fuzzy frequency quantifiers. In this sense, according to the definition given for FROCH-based systems, all the referred parameters and elements have been defined in the framework of a model put forward in the anterior Section, so that the expert can make use of that model in the input cases construction mechanism, which is explicated in the following.
First of all, one possible policy is that the expert could define a fuzzy attribute, through the parameters and elements explained before, every time he or she wants to use it in an input case. This would guarantee that each input case would use the correct (exact) definition, according to the experts’ criterion, for fuzzy definitions of attributes. However, it can be noticed that, if we take into account the FROCH-based definition, a fuzzy valued attribute involves, in turn, the definition of two parameters (i. e.,
a and g ). Furthermore, the expert could also use confidence intervals for a or g , or one fuzzy frequency modifier or one fuzzy modifier. Now, if the same fuzzy attribute is supposed to take part of several input cases, what is normal in real world, the quoted policy would lead to a very inefficient system.On the other hand, it is reasonable to think that, in the context of a maintenance session, the definitions provided by the expert for the same attribute (associated to the same concept in the FROCH) will be kept across different input cases. This assumption has been crucial for the criterion adopted here, which is exposed in the following lines.
In this work, it is proposed that, whenever the expert wishes to construct a fuzzy valued attribute not used yet (for the same concept) in the conceptual hierarchy during the FROCH-based system maintenance session in course, the system must prompt the expert to enter a triple <Tl, Tm, Tr>, whose elements are words different one another and corresponding to the three possible fuzzy values as indicated in (1), (2) and (3), respectively. In addition to this, the expert must include in these the value, which is intended to have the fuzzy attribute under question. Furthermore, two real numbers (and, optionally, their respective confidence intervals), corresponding to the points where the membership functions Tl and Tr, respectively, reach the value 1 (that is,
a and g ), must be provided by the expert. However, if the fuzzy attribute corresponding to the same involved concept was already used to construct a case in the current maintenance session, all what the expert will have to do is to select, amongst Tl, Tm and Tr, the fuzzy value for the current input case.In addition, if the expert wants to use a fuzzy modifier to construct a fuzzy valued attribute (i. e., a fuzzy condition) in an input case, in the system here proposed, he or she will be shown a by-default classification of such modifiers that can be modified at anytime by him or by her. In particular, the expert will be shown the modifiers sets, which have been established in (5), containing several elements, so that these can be renamed or removed. In addition to this, new elements can be added to such sets. With all, once the expert has finished introducing modifications, if any, to the current disposition of modifiers, these will be shown to him or to her every time he or she wishes to make use of fuzzy modifiers during the session in course. Besides, when the expert identifies (or enters) a fuzzy modifier to be used, the system will record the modifiers set to which such a modifier belongs for further processing of the input case in which such a modifier was used (or entered).
To end, with respect to fuzzy frequency quantifiers, a similar modus operand to that employed for fuzzy modifiers is proposed. The nuance to be considered with such quantifiers stems from the fact that the system will also take into account the position that every quantifier possesses in a particular quantifier set, according to the fuzzy quantifiers modelling pointed out in the anterior Section. Hence, when the expert wants to use a fuzzy quantifier, which is not present in any of the quantifiers sets yet, he or she must provide the system with more information. To be precise, in addition to identifying the set in which the new quantifier should be included, the expert must also consider the order of frequency relative to any of the other elements (that is, to state whether the new quantifier implies more or less frequency than another one) that already take part of the set under question. The reason for requiring this information is that fuzzy frequency quantifiers have been modelled according to an ordered sets-based classification
(see Section 3).In order to compare an input case and a rule belonging to the KB, some explicit policy should be adopted in relation to how to match conditions that can involve fuzzy valued attributes defined as indicated earlier. Notice that, if a simple characters string recognition strategy is applied in order to check whether two conditions, which can involve fuzzy valued attributes, are or not the same, some problems can arise. Thus, every expert may give his or her particular definition of certain fuzzy attribute. Furthermore, depending on the (input) case, the same expert could use different definitions for the same fuzzy valued attribute or, what is more significant, he or she could define the underlying attribute as a fuzzy valued one or as a crisp valued one indistinctly. So, the pattern recognition solution can lead to a very inefficient, incomprehensible system, since many definitions with minimal differences among them might be given for the same fuzzy valued attribute.
For example, suppose that the KB contains a rule, written R, defined as "if vegetation.density(1,80) is seldom very high then C". In addition to this, let us assume that the expert who is in charge of maintaining the system, to whom we will call E, is different from the one who entered the cornerstone case containing the condition expressed in R, to whom we will call E’. In this case, by assuming that E wishes to use a fuzzy format for the attribute under question, he or she must define vegetation.density in an hypothetical input case exactly as E’ did in R in order to allow an eventual matching between R and the input case.
As it has been put forward, the same attribute for a given concept can be defined as fuzzy or as crisp (depending on the input case) in FROCH-based systems. This has been taken into account for defining a criterion on which the matching process will be based. In particular, we will define first the matching criterion involving two fuzzy valued attributes corresponding to one of the conditions of the input case and to one of the rules of the KB, respectively. After, by applying some results obtained in the definition of this criterion, we will deal with the problem of having a crisp valued attribute against a fuzzy valued one in the case running process.
Attending to the FROCH-based system definition, some compatibility criterion among two whatever definitions of a fuzzy valued attribute could be defined. More precisely, this criterion can be established by taking into account both the information about the parameters defining the underlying membership functions(i.e.,
a , g and their respective confidence intervals) and the elements of the attribute definition (i. e, the quantifier, the modifier, and the fuzzy value) involving the two fuzzy valued attributes under question. For it, the semantic distance among the elements or parameters implied in a comparison has been considered as a basic factor.Formally, the referred criterion can be stated in a step-by-step process as it is explicated in the following definitions.
First of all, we can group the values associated to each membership function integrating the triple referenced before into semantic compatibility classes by taking into account, for example, that the linguistic tags associated to Tl(x) and Tr(x), respectively, should be different, that is, they should not overlap from the semantic point of view. Formally, the referred classification can be established as follows.
Definition 2: compatible/incompatible fuzzy values
Let < T1, T2, T3> be a triple containing three different linguistic tags associated to the elements of the triple < Tl(x), Tm(x), Tr(x)> and defined according to (1), (2) and (3), respectively; and let V1 and V2 be two elements belonging to the union set ![]() . V1 and V2 are said to be two compatible fuzzy values, written compatible_values (V1, V2), if the following holds:
. V1 and V2 are said to be two compatible fuzzy values, written compatible_values (V1, V2), if the following holds:
![]() where V12 = {V1}È {V2}.
where V12 = {V1}È {V2}.
Otherwise, that is, if the above condition does not hold, p1 and p2 are said to be two incompatible fuzzy values, written incompatible_values (V1, V2).
Definition 3: left/right -side membership functions
Let (a f, g f) be the parameters corresponding to the definition of a fuzzy attribute, written FVA, in a FROCH-based system. Consider also the triple < Tl(x), Tm(x), Tr(x)>, defined according to (1), (2) and (3), respectively. The left-side membership functions associated to (a f, g f), written left_side_mf(a f, g f), is defined as the set {Tl(x), Tm(x)}in the interval [a f, b f].
Similarly, the right-side membership functions associated to (a f, g f), written right_side_mf(a f, g f), is defined as the set {Tm(x), Tr(x)}in the interval [b f, g f].
Definition 4: maximum parameter-based compatibility distance
Let (a f, g f) be the parameters corresponding to the definition of a fuzzy attribute, written FA, in a FROCH-based system; let L = (l1, l2) be the set of linguistic tags associated to those of left-side_mf(a f, g f); and let R = (r1, r2) be the set of linguistic tags associated to those of right-side_mf(a f, g f). The maximum parameter-based compatibility distance for FA, written MPCD, is defined as a real number such that [LEFT_COMPATIBILITY(a f, g f, MPCD) and RIGHT_COMPATIBILITY(a f, g f, MPCD)] holds where
LEFT_COMPATIBILITY(a f, g f, MPCD) = [" x Î [b f - MPCD, b f] $ l i Î L such that ![]() (x) ³ m r(x) where (r Î R) and (r Ï L);
(x) ³ m r(x) where (r Î R) and (r Ï L);
RIGHT_COMPATIBILITY(a f, g f, MPCD) = [" x Î [b f, b f + MPCD] $ r i Î R such that (x) ![]() ³ m l(x) where (l Î L) and (l Ï R); b f =
³ m l(x) where (l Î L) and (l Ï R); b f = ![]() .
.
Lemma
Let (a f, g f) be the parameters corresponding to the definition of a fuzzy attribute in a FROCH-based system. Then, the following equality holds: MPCD = ![]() .
.
By applying the above lemma to the characteristics of the fuzzy memberships functions underlying a FROCH-based system, the following definitions can be written.
Definition 5: parameter-based compatibility range
Let p be a parameter defining a fuzzy membership function associated to a fuzzy valued attribute, written FVA, in a FROCH-based system; and let MPCD be the maximum parameter-based compatibility distance for FVA. The parameter-based compatibility range for p, written PCR(p), is defined as the interval [p - MPCD, p + MPCD].
Definition 6: parameter-based compatibility
Let p, p’ be belonging to the set {a f, b f , g f}, and whose elements are the parameters that define the fuzzy memberships functions Tl(x), Tm(x) and Tr(x), respectively for certain fuzzy attribute in a FROCH-based system; and let PCR(p) the parameter-based compatibility range for p. p’ is said to be compatible with respect to p, written compatible_parameters (p, p’), if p’ Î PCR(p).
It can be noticed that, attending to the previous corollaries, one could argue that if one wants to know the parameters, which are compatible with respect to b f, some redundancy would be produced as there are two statements asserting this compatibility. To avoid this kind of notation redundancies, we can write the compatibility respect to b f by using a new notation.
Definition 7: relative parameter-based compatibility
Let p, pi , 1 £ i £ n, be two parameters defining a fuzzy membership function for a fuzzy valued attribute in a FROCH-based system such that the following holds: compatible_parameters(p, p1) and compatible_parameters(p, p2) and...and compatible_parameters(p, pn). The parameter-based compatibility relative to p, written relative_compatibility(p), is defined as the set { p1 , p2,.., pn}.
So far, we have formally established the definitions and use of compatibility classes into a same fuzzy attribute according to its definition parameters (that is, a and g ). However, the objective pursued in this subsection is more ambitious in that we attempt to establish a compatibility criterion between two fuzzy attributes in a FROCH-based system. To reach this goal, we can establish some principles, which will constitute the foundation for a further definition of the referred criterion.
Firstly, we can extend the maximum parameter-based compatibility distance concept to the case of two (in general) different fuzzy attributes. For it, we will take into account the following principle.
Principle 1: maximum distance
Let f1 and f2 be two fuzzy valued attributes belonging to a FROCH-based system, and defined, respectively, as "concept.attribute(a i, g i)". A necessary condition for f1 and f2 to be semantically compatible is that pj Î PCR(pk), where pj Î {a j, b j, g j); pk Î {a k, b k, g k}; b i = ![]() ; i, j, k = 1, 2.
; i, j, k = 1, 2.
Secondly, by considering what definition 2 states, we can restrict the parameters that could potentially be semantically inter-compatible to those whose values belong to the same class.
Principle 2: non-incompatible values
Let f1 and f2 be two fuzzy valued attributes belonging to a FROCH-based system, and defined, respectively, as "concept.attribute(a i, g i) is valuei", i = 1, 2. A necessary condition for f1 and f2 to be semantically compatible is that compatible_values (value1, value2).
By analysing the two compatibility classes defined above, it is easy to note that the two geometrical regions where such classes exist have interesting properties respect to the values that the respective membership functions involved in them take. This fact can be expressed in a formal step-by-step process as follows.
From what has bee considered so far, someone could argue that a criterion about the semantic compatibility between two fuzzy valued attributes, where the difference is only in the parameters or in the values, can be derived from the logic conjunction of the two principles indicated earlier. This idea can be founded on the fact that all the so-obtained results can be applied to many situations. Consider, for example, the distributions ((a) - (e)) shown in Figure 1.

It can be noted that all the cases (a) - (e) in Figure 2 hold the two principles mentioned previously. Moreover, by applying Definition 6 to each of the above cases, the following is obtained:
(a) relative_comp(
(b) relative_comp(
a 1) = {b 1, a 2, b 2}; relative_comp(g 1) = {b 1, g 2};(c) relative_comp(
a 1) = {b 1, a 2}; relative_comp(g 1) = {b 1, b 2, g 2};(d) relative_comp(
a 1) = {b 1, a 2, b 2}; relative_comp(g 1) = {b 1, g 2};(e) relative_comp(
a 1) = {b 1, a 2, b 2}; relative_comp(g 1) = {b 1, g 2}.However, problems still remain when one of those fuzzy valued attributes is composed by parameters very close each other and, in turn, all of them being very far from one of the pairs (
a , g ). Figure 2 illustrates this phenomenon. Besides, when this occurs, although the two necessary conditions underlying Principle 1 and Principle 2, respectively, hold, it seems not to be reasonable to consider the possibility of the two fuzzy valued attributes under question to be compatible.
Figure 2. Accumulation of parameters.
Formally, this situation can be expressed in the following principle:
Principle 3: maximum distance
Let f1 and f2 be two fuzzy valued attributes belonging to a FROCH-based system, and defined, respectively, as "concept.attribute(
a i, g i) is valuei"; and let MPCDi be the maximum parametric compatibility distance for fi, i = 1, 2. A necessary condition for f1 and f2 to be semantically compatible is that the following holds:{[(
g j £ g k) and (a j ³ a k)] ® (MPCDj ³ K j* MPCDk)}, j¹ k = 1,2where
K j = min{
b j - MAXa j, MINg j - b j};MAX
a j =Based on the three principles exposed before, the following definition can be derived:
Definition 8: compatible/ incompatible definition parameters
Let f1 and f2 be two fuzzy valued attributes belonging to a FROCH-based system, and defined, respectively, as "concept.attribute(
a k[Ia k] , g k[ Ig k] ) is valuek"; let pk be (a k, g k); let Kj be in accordance with Principle 3; and let MPCDk be the maximum parametric compatibility distance for fk, k = 1, 2. p1 and p2 are said to be compatible definition parameters, written compatible_parameters (p1, p2) if (compatible_values(value1, value2)) and (within_compatible_ranges(pi, pj)) and (sufficient_distance(pi, pj)) holds, wherewithin_compatible_ranges(pi, pj) = ![]() ;
;
sufficient_distance(pi, pj) = ![]()
Now, if we go one step beyond, in the sense of considering also fuzzy frequency quantifiers, another designing principle, operating on the frequency sets pointed out in Section 3, can be established.
Principle 4: frequency compatibility
A fuzzy frequency quantifier belonging to the I
È L must not be considered as semantically compatible to another one not belonging to such a union set.The above principle can be used to formally define the compatibility it alludes to as follows:
Definition 9: compatible/ incompatible fuzzy frequency quantifiers
Let q1 and q2 be two fuzzy frequency quantifiers such that qk belongs to the union set H
È L È F È I È UNq, k = 1, 2; where H, L, F and I respond to the definition given in (9), while UNq stands for the fact that some quantifier is unspecified. So, UNq can be expressed as the set {"unspecified_quantifier"}. Moreover, we will assume that an unspecified quantifier is a synonym concept of "always". Under these conditions, q1 and q2 are said to be two compatible fuzzy frequency quantifiers, written compatible_quantifiers(q1, q2), if the following logic condition holds:[(q12
Í INFERIOR_FREQS) or (q12 Í SUPERIOR_FREQS)]where
q12 = {q1}
È {q2}; INFERIOR_FREQS = (I È L); SUPERIOR_FREQS = (F È H È UNq).Otherwise, that is, if the above logic equation does not hold, q1 and q2 are said to be two incompatible fuzzy frequency quantifiers, written incompatible_quantifiers(q1, q2).
The anterior principle can also be used when fuzzy modifiers are present in a fuzzy valued attribute. The nuance to be considered in this case is that a modifier can belong to several compatibility classes
Formally, the compatibility concerning fuzzy modifiers has been established by means of the following definition.
Definition 10: compatible/incompatible fuzzy modifiers
Let m1 and m2 be two fuzzy modifiers such that qk belongs to the union set P
È N È IS_NOT È UNm, k = 1, 2; where P, N, and IS_NOT respond to the definition given in (5), while UNm accounts for the fact that some modifier is unspecified. So, UNq can be expressed as the set {"unspecified_modifier"}. Moreover, we will assume that the presence of an unspecified modifier means that the parameter d takes the value 1. Under these conditions, m1 and m2 are said to be two compatible modifiers, written compatible_modifiers(m1, m2), if the logic conditionM1=![]() ; M2=
; M2=![]() ;
;
M3=![]() ; M4 =
; M4 = ![]() ;
;
Otherwise, that is, if the above logic equation does not hold, q1 and q2 are said to be two incompatible fuzzy modifiers, written conflicitve_modifiers(q1, q2).
By considering the previous definitions, a compatibility/conflictivity criterion to be applied to eventually fuzzy valued attributes in the context of a FROCH-based system can be derived as follows.
Definition 11: compatible fuzzy valued attributes
Let FVA1 and FVA2 be two fuzzy valued attributes represented, according to definition 1, as "ci.ai(pi) is [qi
] [ mi] vi" respectively, where pi = (a i[Ia i] , g i[Ig i] ), i = 1, 2. FVA1 and FVA2 are said to be two compatible fuzzy valued attributes, written compatible_val_atts (FVA1, FVA2), if [(EQUAL12) or ((EQUAL_ca (FVA1, FVA2) and (COMPATIBLE_vpmq (FVA1, FVA2))] holds, whereEQUAL12 = (FVA1 = FVA2);
EQUAL_ca (FVA1, FVA2) = (c1.a1 = c2.a2); and
COMPATIBLE_vpmq (FVA1, FVA2) = [(compatible_parameters(p1, p2)) and (compatible_modifiers(m1, m2)) and (compatible_quantifiers(q1, q2))].
Similarly, the following definition can be established:
Definition 12: incompatible fuzzy valued attributes
Let FVA1 and FVA2 be two fuzzy valued attributes represented, according to definition 1, as "ci.ai(pi) is qimivi" respectively, where pi = (
a i[Ia i] , g i[Ig i] ), i = 1, 2. FVA1 and FVA2 are said to be two incompatible fuzzy valued attributes, written incompatible_val_atts (FVA1, FVA2), if [EQUAL_ca (FVA1, FVA2) and (NOT(COMPATIBLE_vpmq(FVA1, FVA2) )] holds, where EQUAL_ca (FVA1, FVA2) and COMPATIBLE_vpmq (FVA1, FVA2) are defined as in previous definition.When a case is entered to a FROCH-based system, several situations can be distinguished, depending on the nature of the attributes implied in the matching process, namely, either fuzzy or crisp. Thus, the crisp valued attributes can respond to various formats. Here, we will consider the character string-based one and the numeric interval-based one. All these possibilities are analysed in the following lines.
6.2.1 Fuzzy valued attributes versus character string-like valued attributes
A representative example of this situation can be "vegetation.height(5,40) is high versus vegetation.height = medium". By assuming that the same pair (concept, attribute) is referenced in both conditions, the criterion to be followed will consist of checking whether the values (and, eventually, the modifiers and the quantifiers) are compatible. Moreover, if they are found to be compatible and the rule involved in the comparison process possesses siblings in the MCRDR structure, the crisp valued attribute under question will be replaced by the fuzzy valued attribute in further comparisons for the current input case. In this way, given an input case, the matching process involving sibling rules will take place in a context of a more precise knowledge.
Formally, the compatibility criterion can be stated as follows:
Definition 13: compatible non-numerical crisp valued attributes
Let FVA 1 and CSVA 2 be a fuzzy valued attribute and a character string-like valued attribute in a FROCH-based system and represented, respectively, as follows :
FVA 1 = "concept1.attribute1(p 1) is [q1
] [m1] v1"; CSVA 2 = "concept2.attribute2 = [q2] [m2] v2"Where p1 = (
a 1[Ia 1] , g 1[Ig 1] )FVA 1 and CSVA 2 are said to be s-compatible, written s-compatible(FVA 1, CSVA 2), if (concept1.attribute1 = concept2.attribute2) and (compatible_values(v1, v2)) and (compatible_modifiers(m1, m2)) and (compatible_quantifiers(q1, q2)) holds.
6.2.2 Fuzzy valued attributes versus numeric interval-like valued attributes
A typical example of this case is "height(5,40) is high versus height
Î [5,12] ". By assuming that the same pair (concept, attribute) is referenced in both conditions, the system will check whether the interval underlying the crisp valued attribute under question is included in the definition of the fuzzy attribute. If so, the system will determine whether the linguistic tag referenced in the fuzzy attribute corresponds to the interval into which the interval associated to the crisp attribute can be allocated. Finally, the modifiers and the frequency quantifiers, if any, will be confronted to check compatibility. This entire process can be expressed in a formal manner in a step-by-step process as follows:Definition 14: active interval
Let (
a [Ia ] , g [Ig ] ) be a pair containing the parameters and their respective confidence intervals corresponding to the definition of a fuzzy attribute, written FVA, in a FROCH-based system; let < T1, T2, T3> be a triple containing three different linguistic tags associated to the respective elements of the triple < Tl(x), Tm(x), Tr(x)>, defined according to (1), (2) and (3), respectively; let C, A be the concept and the attribute, respectively, underlying FVA.; and let v be the value defined in FVA such that v Îactive_interval (C.A, FVA) = 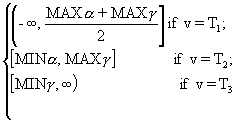
where
MAX
a =MIN
a =Now, the following definition can be established:
Definition 15: compatible numeric crisp valued attribute
Let FVA 1 and NIVA 2 be a fuzzy valued attribute and a numeric interval-like valued attribute in a FROCH-based system and represented, respectively, as follows :
FVA 1 = "concept1.attribute1(p 1) is [q1
] [m1] v1";CSVA 2 = "concept2.attribute2
Î (vinf, vsup)"where
p1 = (
a 1[Ia 1] , g 1[Ig 1] )FVA 1 and NIVA 2 are said to be n-compatible, written n-compatible(FVA 1, NIVA 2), if (concept1.attribute1 = concept2.attribute2) and (compatible_values(v1, v2)) and (compatible_modifiers(m1, m2)) and (compatible_quantifiers(q1, q2)) and [(vinf, vsup)
Î active_interval(concept1.attribute1, FVA 1)] holds.By using previous definitions, the condition for a given rule in a FROCH-based system to by fired by an input case, can be established as follows:
Definition 16: fired fuzzy ripple down rule
Let CRi be a condition of a rule, written R; let CIj be a condition for an input case, written I; and let CRi and CIj being respectively represented (according to the representation format adopted here for FROCH-based system) as follows:
Ck = ![]()
Where: Ck
Î {CRk, CIk}; k Î {i, j}; pk = (a k[Ia k] , g k[Ig k] ); nk = number of values involved in ck.akR is said to be fired by I, written fired (R, I) if
" CRi Î R, $ CIj Î I, such that compatible_valued_attributes(CRi, CIj ) holds Where:compatible_valued_attributes (CRi, CIj)=

match(CRi, CIj)
=R =![]() ; I =
; I = ![]() .
.
Once a rule has been fired by an input case, the expert will be shown the conclusion associated to such a rule. Thus, as it has been put forward earlier, since conclusions can also be represented by means of fuzzy valued attributes, a number of these ones concerning the same attribute might be produced. This problem is addressed in the next Section.
As it has been pointed out already in this work, if multiple conclusions are feasible in the system (that is, if it is an MCRDR system) and provided that they can encompass fuzzy valued attributes, semantic conflicts among valued attributes can arise when experts are shown a set of conclusions after running an input case. Similarly to the problem addressed in previous Section about how to define the matching conditions between an input case and a rule in a FROCH-based system, the system should have a mechanism for managing the situation where multiple conclusions about the same valued attributes are produced by the system.
If it is taken into account what has been put forward in Section 2, it can be said that the deeper in an MCRDR structure, the more refined the knowledge it contains. So, in case that multiple conclusions about the same attribute (for the same concept) are generated by the system, this factor (i. e., the conclusion depth in the rules base structure) should be considered. Besides, several conclusions alluding to the same feature at the same depth in the rule structure could be generated. If so, inter-compatible conclusions can be grouped into compatibility classes. In this manner, a potential reduction of the expert’s task is achieved.
In addition to grouping the conclusions into compatibility classes, we can make use of the possibilities that fuzzy logic offers to help the experts to decide which conclusion concerning a certain feature should be considered by assuming that the conclusions under consideration are allocated at the same depth. For it, we can exploit the fact that fuzzy membership functions can be propagated from antecedents to consequents in the rules.
With all, if there are rules matching an input case (I), the following algorithm to acquire conclusions is proposed:
Conclusion Acquisition (CA) algorithm
Li =
f {List of ordered conclusions (according with their certainty) associated to Ci } doif Card(Ci) > 1 then
group the conclusions in Ci into compatibility classes such that, for each compatibility class, the conclusion having the greatest depth in the MCRDR structure is selected as the "representative" one for the compatibility class under question; the representative conclusions C1(concepti.attributei), C2(concepti.attributei), .., Cm(concepti.attributei) will be obtained;
classify the so-obtained conclusions according to the depth of their location in the MCRDR structure in a decreasing order; the sets of representative conclusions C1(concepti.attributei),C2(concepti.attributei),.., Cs(concepti.attributei) will be obtained;
for every Cj(concepti.attributei) do
if Card(Cj(concepti.attributei)) > 1 then
group the conclusions in Cj(concepti.attributei) into rule antecedent-based membership function values in a decreasing order; record each value together with the conclusion to which that value is associated;
Li = Li
È Cj(concepti.attributei);else Li = Li
È Ciwhere the compatible conclusions are obtained from the following definition:
Definition 17: compatible/incompatible conclusions
Let C1 and C2 be two conclusions involving the valued attributes VA1 and VA2, respectively. C1 and C2 are said to be two compatible conclusions, written compatible_conclusions (C1, C2), if compatible_valued_attributes (VA1, VA2) holds. In an analogous way, they are said to be two incompatible conclusions, written incompatible_conclusions (C1, C2), if not(compatible_valued_attributes(VA1, VA2)) holds.
Once the conclusions have been grouped, the following algorithm will be carried out in this approach:
Conclusion Show (CS) algorithm
For i=1 to n do {n = number of pairs (concept,attribute)}
for j=1 to mi do { mi = number of elements in Li}
show Lij to the expert;
if he or she does not agree with Lij then
ask the expert to enter a new conclusion, NC, such that it will only affect the fired rule(s) containing Lij or another compatible conclusion(s) situated at the same depth in the MCRDR structure than Lij;
if j < mi then
for k = j + 1 to mi do
if compatible_conclusions(NC, Lik) then
Li = Li \{ Lik}; mi = mi - 1
Concerning the CA algorithm, we must clarify how to proceed with the propagation of membership function values from the antecedent to the consequent part of a fired rule. For it, there are several methods (Bárdossy, 1995), including the algebraic product-sum, the Hamacher product-sum, the Einstein product-sum, and the Bounded difference-sum. In this article, the algebraic product has been chosen, as it provides a good alternative and is computationally parsimonious. Through this method, the membership function value of the consequent of a rule is calculated as the product of the membership function values corresponding to the each of the sub conditions forming the antecedent of the rule under question. Therefore, the problem will be reduced to how to calculate the membership function value for each sub condition of the antecedent.
To calculate the membership function value (MFV) associated to a sub condition, it must be considered the fact that rules as well as input cases can include crisp or fuzzy valued attributes. In this sense, if a rule condition is crisp, an MFV equals to 1 will be assumed. Otherwise, the MFV will be dependent of the nature of the input case condition that matches the rule condition under question. For analysing the possible situations that can arise when the condition of the rule under question, written COND’, is a fuzzy valued attribute, we will attend to the nature (crisp or fuzzy) of the condition, written COND, in the input case.
In this situation, the MFV for COND’, written MFV(COND’), will be calculated as follows:
MFV(COND’) = ![]()
Where Minf = 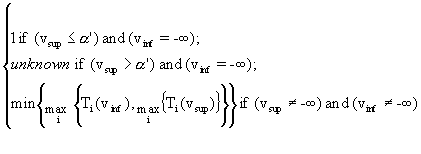
Msup = 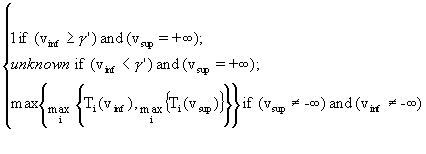
vinf represents the inferior limit value of the attribute underlying COND;
vsup represents the superior limit value of the attribute underlying COND;
Ti(v) represents the fuzzy membership function valued for v and associated to the ith element of the triple defining the attribute that underlies COND’; i = 1, 2, 3; v
When the condition under question in the input case contains a fuzzy valued attribute, the method proposed here to calculate the membership function value of the rule condition that matches the input case condition can be written as follows:
MFV(COND’) = ![]()
where
C.A stands for the concept and the attribute, respectively, referenced in both COND and COND’;
Minf and Msup are according to the definition given in the previous sub-section.
At this point, it is possible to obtain a membership function value for a conclusion in a certain rule by taking into account all the membership function values of the condition(s) in the antecedent of such a rule. For it, it can be noticed that three possible types of value for MFV have been considered, namely, numeric ones, interval-based ones and those equals to "unknown". With all, by using the above assumptions and the notation employed before, a formula to propagate fuzzy values from antecedent to consequent parts in a rule is proposed in the following.
Let r be a rule in a FROCH-based system represented as ![]()
MFCO(r) = ![]()
where
MFCOinf (r) = 
MFCOsup (r) = ![]()
inf(MFV(Ci))=![]() sup(MFV(Ci))=
sup(MFV(Ci))=![]()
In addition, if the expert disagrees with some conclusion and, according to step (S4.2) pointed out in Section 4, the system must decide where to add the new rules to be entered by the expert, each of them corresponding to a different wrong conclusion. The way to do that will be kept in FROCH-based systems, that is, the method used in MCRDR will be adopted. To be precise, given a wrong conclusion produced by the system, such a method adds the rule providing the right conclusion at the end of the path going to the rule that produced the wrong conclusion. With this, the system corrects the KB.
With MCRDR, various cornerstone cases may reach a new rule and the higher in the tree, the more cases can reach the rule. Moreover, every case that may reach its parent rule can potentially fire on the new rule. Therefore, the new rule should differentiate the input case from all the cornerstone cases except from those having their conclusion the same as that provided by the new rule. In other words, MCRDR possesses a number of cornerstone cases for a given rule, which must be prevented from satisfying the new rule.
With the purpose of making a new rule sufficiently precise, a very simple algorithm for selecting conditions is used in MCRDR. This algorithm reaches the goal of providing the new rule with sufficient precision so that it can uniquely be fired by the case it is being added for and no other cornerstone cases, provided that these do not involve a different conclusion. Given a new rule (corresponding to a wrong conclusion) to be added at a particular location, the mentioned algorithm works as follows (Kang, 1996):
With respect to the construction of a difference list between an input case and a cornerstone case, the features differentiating these cases must include at least a basis for a justification as to why the conclusions for the cases should differ. As it has been put forward in Section 2, the domain is supposed to be a closed world. Therefore, a negation of a condition belonging to the cornerstone case should be satisfied by the input case. Formally, given an input case, written I, and composed by n > 1 conditions, and a cornerstone case, written C, and composed by m > 1 conditions, the difference list, written D, can be defined as follows: D = Dinput
È DcornerstoneWhere: Dinput = { Ii
| (Ii Ï C)}; Dcornerstone = { NOT(Cj)| (Cj Ï I)}; I =It can be noticed that, in general, C
Ç I ¹ f .In the particular case of FROCH-based systems, given the knowledge representation schema adopted in this article, the calculation of both Dinput and Dcornerstone must be done according to the compatibility criteria (by assuming that there can be fuzzy valued attributes involved in such an schema) pointed out before. In the following lines, and by taking into account previous definitions, this issue is analysed in depth
Definition 18: F-non-membership
Let A be a rule condition represented as follows:
A = ![]()
and let C be a case in a FROCH-based system to which A is confronted. A is said to be a non-member of C in the mentioned context, written F-non-member (A, C), if not(
$ Cj Î C s. t. compatible_valued_attributes (Cj, A)) where C =By taking into account last definition and the classic method to construct difference lists in RDR-based systems, a new definition for difference list in the context of FROCH-based systems can be expressed as follows:
Definition 19: F-difference list
Let I and C be an input case and a cornerstone case composed respectively by n and m conditions; n, m
³ 1. The difference list between I and C in the context of a FROCH-based system, written F-difference list (I, C), is defined as the union set FDinput È FDcornerstoneWhere FDinput = {Ii
| F-non-member(Ii, C)}; FDcornerstone = {NOT(Cj)| F-non-member (Cj, I)};I = ![]() ; C =
; C = ![]() .
.
Ripple down rules (RDR) is a knowledge acquisition technique whose aim is to use the knowledge only in the context provided by the expert, this context being the sequence of rules evaluated to give a certain conclusion. With this approach, rules are never removed or corrected, only added. This addition only occurs when the expert does not agree with a conclusion supplied by the system and, then, he or she wishes to correct such a conclusion.
Fuzzy terms are widely used in real-life problems to which current RDR-based systems may be applied. Although fuzzy logic is normally used to deal with fuzzy domains, those systems only allow to assign crisp values to fuzzy-by-nature attributes. Moreover, current developments of RDR do not allow experts to use fuzzy terminology in a natural, compact manner. The knowledge that can be acquired and represented in such systems is, hence, restrictive and non-natural from the experts’ point of view. In this paper, a formal approach that can be used to acquire and represent fuzzy domain knowledge through the most recent versions of RDR-based systems has been presented.
We have defined a model that allows experts to use fuzzy modifiers as well as fuzzy frequency quantifiers when they construct cases for a further processing by the system. Moreover, based on some well-defined assumptions about the kind of fuzzy terms that can be represented in our model, a new methodology for running cases, which can include both fuzzy and crisp values, has been proposed.
By considering the nature of RDR systems and some properties relative to fuzzy processing, two algorithms, concerning the acquisition of conclusions and their later presentation to the experts, have been designed. The most important factors considered in these algorithms are the rule base structure, the possibility of propagating fuzzy membership values from antecedents to consequents in rules and the model proposed here for running cases. With all, in this model, experts can be helped to make their choice when they are shown several conclusions alluding to the same feature. Finally, according to some well-established compatibility criteria among the conditions involving fuzzy valued attributes, a new method for identifying the conditions that must integrate a new rule to be added to the system has been put forward. Moreover, to illustrate the usefulness of the mathematical artefacts designed in this work, we have shown some examples that stem from a real problem involving environmental planning by assessment in Spain.
The approach presented is concerned with the acquisition/representation of fuzzy domain knowledge in RDR-based systems. Therefore, the formal model we have exposed can be viewed as an extension of current RDR-based systems to deal with fuzzy domains in a direct, natural way. In this sense, our approach is complementary to work on MCRDR systems (Kang, 1996) and the ROCH approach (Martínez-Béjar et al., 1997b), as these provide methods to apply RDR-based systems to other more complex tasks and to construct RDR ontological frameworks, respectively.
Although the theoretical model proposed here is a first step forward in making fuzzy domain knowledge feasible and well founded, much work remains to be done. For instance, applying the logical negation to a fuzzy condition, represented as indicated in our model, in order to obtain the differences different cases can lead to experts’ difficulties in understanding the meaning of such a negation. Hence, the system should provide the experts with semantically equivalent sentences having a better degree of comprehensibility. Moreover, an implementation of the model proposed here is in course. In this sense, to evaluate the model through the feedback obtained from the experts’ working with an implementation of such a model is fundamental to know the real success of this approach.
References
Adlassnig, K.-P., and Kolarz, G. (1982). CADIAG-2: Computer-assisted medical diagnosis using fuzzy subsets, In M. M. Gupta and E. Sanchez (Eds.), Approximate Reasoning in Decision Analysis, 219-247, New York: North-Holland.
Adlassnig, K.-P., Kolarz, G., and Scheithauer, W. (1985). Present state of the medical expert system CADIAG-2, Methods of Information in Medicine, 24, 13-20.
Baldwin, J. F. (1992). Evidential support logic, frill and case based reasoning, International Journal of Intelligent Systems, 8(9), 939-961.
Baldwin, J. F., and Pilsworth, B. W. (1980). Axiomatic approach to implication to approximate reasoning with fuzzy logic, Fuzzy Sets and Systems, 3: 193 - 219.
Bárdossy, A. (1995). Fuzzy Rule-Based Modelling with Applications to Geophysical, Biological and Engineering Systems, CRC Press, Inc
Binaghi, E., De Giorgi, O., Maggi, G., Motta, T., and Rampini, A. (1993). Computer-assisted diagnosis of post-menopausal osteoporosis using a fuzzy expert system shell, Computers and Biomedical Research, 26: 498-516.
Buckley, J. J., Siler, W., and Tucker, D. (1986). A fuzzy expert system, Fuzzy Sets and Systems, 20: 1 - 16.
Catlett, J. (1992). Ripple-down-rules as a mediating representation in interactive induction, In Proceedings of the Second Japanese Knowledge Acquisition for Knowledge-Based Systems Workshop, 155-170, Kobe, Japan.
Clancey, W. J. (1991). Book review of 'The Invention of Memory', Artificial Intelligence, 50(2): 241-284.
Clancey, W. (1993). The frame of reference problem in the design of intelligent machines, In K. VanLehn and A. Newell (Eds.), Architectures for Intelligence: The twenty second Carnegie Symposium on Cognition, Hillsdale, Lawrence Erlbaum Associates.
Compton, P. (1992). Insight and knowledge, In AAAI Spring Symposium: Cognitive Aspects of Knowledge Acquisition, 57-63, Stanford University.
Compton, P., Horn, R., Quinlan, R. and Lazarus, L. (1989). Maintaining an expert system, In J. R. Quinlan (Eds.), Applications of Expert Systems, 366-385, London, Addison Wesley..
Compton, P. and Jansen, R. (1989). Knowledge in context: a strategy for expert system maintenance, In C. J. Barter and M. J. Brooks (Eds.), AI'88, 292-306, Berlin, Springer-Verlag.
Compton, P. and Jansen, R. (1990). A philosophical basis for knowledge acquisition, Knowledge Acquisition, 2: 241-257.
Compton, P. and Preston, P. (1990). A minimal context based knowledge acquisition system, in Knowledge Acquisition: Practical Tools and Techniques AAAI-90 Workshop, Boston,
Compton, P., Preston, P., Kang, B. and Yip, T. (1994). Local patching produces compact knowledge bases, In L. Steels, G. Schreiber & W Van de Velde, A Future for Knowledge Acquisition: Proceedings of EKAW'94, 104-117, Berlin, Springer Verlag.
Compton, P., Preston, P. and Kang, B. (1995). The use of simulated experts in evaluating knowledge acquisition, In B. Gaines & M. Musen, Proceedings of the 9th AAAI-Sponsored Banff Knowledge Acquisition for Knowledge-Based Systems Workshop, 12.1-12.18, Banff, Canada, University of Calgary.
Daniels, J. E., Cayton, R. M., Chappell, M. J., and Tjahjadi, T. (1997). Cadosa: a fuzzy expert system for differential diagnosis of obstructive sleep apnoea and related conditions, Expert Systems with Applications, 12(7): 163-177.
Dreyfus, H. and Dreyfus, S. (1988). Making a mind versus modelling the brain: artificial intelligence back at a branchpoint, Daedalus, 117(Winter): 15-43.
Dubois, D., and Prade, H. (1988). Possibility Theory, an Approach to Computerised Processing of Uncertainty, New York, Plenum Press.
Edwards, G., Compton, P., Malor, R., Srinivasan, A., and Lazarus. (1993). PEIRS: a pathologist maintained expert system for the interpretation of chemical pathology reports, Pathology, 25: 27-34.
Fathi-Torbaghan, M., and Meyer, D. (1994). MEDUSA: A fuzzy expert system for medical diagnosis of accute abdominal pain, Methods of Information in Medicine, 33: 522-529.
Gaines, B. (1991). Induction and visualisation of rules with exceptions, 6th AAAI Knowledge Acquisition for Knowledge Based Systems Workshop, 7.1-7.17, Bannf.
Gaines, B. R. and Compton, P. J. (1992). Induction of ripple down rules, AI '92 Proceedings of the 5th Australian Joint Conference on Artificial Intelligence, 349-354, Hobart, Tasmania, World Scientific, Singapore.
Gisolfi, A., and Di Lascio, L. (1995). POTCLAS: a fuzzy expert system for the classification of archaeological pottery fragments, International Journal of Expert Systems, 8(2):145-164.
Grabot, B., and Caillaud, E. (1996). Imprecise knowledge in expert systems: a simple shell, Expert Systems with Applications, 10(1): 99-112.
Grabot, B., Geneste, L., and Dupeaux, A. (1994). Multi-heuristic scheduling: three approaches to tune compromises, Journal of Intelligent Manufacturing, 5: 303-313.
Horn, K., Compton, P. J., Lazarus, L. and Quinlan, J. R. (1985). An expert system for the interpretation of thyroid assays in a clinical laboratory, Aust Comput J 17 : 7-11 .
Hwang, G-J. (1995). Knowledge acquisition for fuzzy expert systems, International Journal of Intelligent Systems, 10:541-560.
Kandel, A. (1990). Fuzzy mathematical techniques with applications, Reading, MA, Addison-Wesley.
Kang, B. H. (1996). Validating Knowledge Acquisition: Multiple Classification Ripple Down Rules, PhD Thesis, University of New South Wales, Sydney, Australia.
Kang, B. and Compton , P. (1992). Knowledge acquisition in context: the multiple classification problem, In Proceedings of the Pacific Rim International Conference on Artificial Intelligence, 847-854, Seoul.
Kang, B. H., Compton, P., and Preston, P. (1995). Multiple classification ripple down rules: evaluation and possibilities, In Proceedings of the 9th Knowledge Acquisition for Knowledge Based Systems Workshop, 17.1-17.20, SRDG Publications, Department of Computer Science, University of Calgary, Calgary, Alberta, Canada.
Martínez-Béjar, R., Cádenas, J. M., and Martín-Rubio, F.(1997a). Fuzzy logic in landscape assessment, In Proceedings of the European Symposium on Intelligent Techniques, 234-238, Bari, Italy.
Martínez-Béjar, R., Benjamins, V. R., Compton, P., Preston, P., and Martín-Rubio, F.,. (1997b). A formal framework to build domain knowledge ontologies for ripple down rules-based systems, In Press.
Richards, D., and Compton, P. (1997a). Combining formal concept analysis and ripple down rules to support the reuse of knowledge, in Proceedings of the 9th International Conference of Software Engineering and Knowledge Engineering SEKE’97, Madrid, Spain.
Richards, D., and Compton, P. (1997b). Knowledge acquisition first, modelling later, To appear in Lectures Notes in Artificial Intelligence, Springer-Verlag, Berlin.
Scheffer, T. (1996). Algebraic foundation and improved methods of induction of ripple down rules, In Proceedings of Pacific Knowledge Acquisition Workshop PKAW’96, 279-292, Coogee, Australia.
Srinivasan, A., Compton, P., Malor, R., Edwards, G. and Lazarus, L. (1992). Knowledge acquisition in context for a complex domain, In B. Wielinga, J. Boose and B. Gaines (Eds.), Proceedings of the Fifth European Knowledge Acquisition Workshop, Pergamon.
Sugeno, M. (1985). An introduction survey to fuzzy control, Information Sciences, 36: 149-223.
Watanabe, T. (1991). Job-shop scheduling using fuzzy logic in a computer integrated manufacturing environment, In G. Lasker, T. Koizumi and J. Pohl (Eds.), 5th International Conference on Systems Research, Informatics and Cybernetics, 150-158.
Winograd, T. and Flores, F. (1987). Understanding computers and cognition, Reading, MA, Addison Wesley.
Yager, R. R. (1984). Approximate reasoning as a basis for rule-based expert systems, IEEE Transactions on Systems, Man, and Cybernetics, 14: 636 - 643.
Zadeh, L. A. (1965). Fuzzy sets, Information and Control, 8: 338-353.
Zadeh, L. A. (1983). The role of fuzzy logic in the management of uncertainty in expert systems, Fuzzy Sets and Systems, 8(3): 199 - 227.