Evaluating Conceptual Modeling Languages
Tim Menzies  , Robert F. Cohen
, Robert F. Cohen  , Sam Waugh
, Sam Waugh 
 Artificial Intelligence Department,
Artificial Intelligence Department,
School of Computer Science and Engineering,
University of NSW, Australia, 2052
 Department of Computer Science and Software Engineering,
Department of Computer Science and Software Engineering,
University of Newcastle, NSW, Australia, 2308
 Defence Science and Technology Organisation,
Defence Science and Technology Organisation,
Air Operations Division, Melbourne, Australia, 3001
tim@menzies.com
rfc@cs.newcastle.edu.au
sam.waugh@dsto.defence.gov.au
http://www.cse.unsw.edu.au/ timm
February 20, 1998
Abstract:
An important assumption for many KA researchers is structure
preservation ; i.e. conceptual models can be converted in a
straight forward manner into a design for an implementation.
This assumption may not always hold. Seemingly trivial variants in a
qualitative conceptual models can block pragmatically desirable
properties such as KB-testability and KB-maintainability.
KB-testability and KB-maintainability are an important property: we
must not build knowledge bases that are untestable or unmaintainable.
Hence, we argue against using these features within conceptual models.
The tools used for identifying these features (instance generators,
graph theory, studying KB-testability and KB-maintainability) are
quite general and could be used to find restrictions to other
conceptual modeling languages.
Pragmatics must take precedence over elegance,
for Nature cannot be impressed.
Coggin's Law (from [Booch, 1994])
This paper is about pragmatic limits to conceptual modeling. We
disagree with the
conventional wisdom in the knowledge acquisition field (KA)
(e.g [Wielinga et al., 1992, Shadbolt & O'Hara, 1997, van Harmelen & Aben, 1996, Benjamins & Aben, 1997]) that:
- The conceptual modeling language should be expressive enough to
capture all the expert's knowledge.
- Starting with a conceptual model of the required expertise, various
structure preserving transformations can be applied to produce
a working system. Such structure preserving transforms are
straightforward conversions of the high-level structures in the
conceptual model into the design model.
Experience with the QCM qualitative modeling language suggests that
not all conceptual models can be structurally preserved. QCM is used
in the earliest stages of KA. For our experts, it represents their
ideas in a similar
manner to how they first express those ideas. It can represent
under-specified ideas
and tolerate inconsistencies in an evolving
specification. Further, QCM has a built-in validation engine which can
help experts to review and improve their current specification.
Hence, we say that QCM is a conceptual
modeling language [Feldman et al., 1989a, Menzies, 1995, Menzies, 1996a, Menzies & Compton, 1997, Waugh et al., 1997]. We will use
the criteria of KB-testability and KB-maintainability (defined below),
to demonstrate the need for certain restrictions to QCM conceptual
models. Roughly speaking, KB-testability means checking if a theory
of X can reproduce known behaviour of X; and
KB-maintainability means checking if we can tell if some change is an
improvement to a theory. Seemingly trivial variants in the conceptual
modeling language will be shown to have a large impact on
KB-testability and KB-maintainability. We will propose below
restrictions on size, connectivity, the use of conjunctions, and the
types of temporal causal connections. In these restrictions are
obeyed, then we have a necessary, but not sufficient proof, that a
theory will be testable and maintainable. We only claim that if a
system does not satisfy our criteria then it will not support
KB-testability and KB-maintainability (and leave the converse
statement to future work).
Our restrictions apply to any knowledge base (KB) which can be
represented as a cyclic dependency and-or graph of literals. Many such
representations exist including propositional rule bases used in a
match-select-act loop, recursive ground horn clauses, or qualitative
theories used for simulations. Further, the methods used here
(instance generators, graph theory, analysis of KB-testability and
KB-maintainability) are quite general and could be used to find
restrictions to other conceptual modeling languages.
We have argued
elsewhere [Menzies, 1997] that the KE field urgently needs such general
evaluation methodologies.
Our conclusions come from a theoretical and empirical analysis of a
KB-testability and KB-maintainability algorithm. We take care to
distinguish this work from the worst-case time complexity research
of the knowledge representation (KR) community. Restrictions
motivated by potentially exponential runtimes do not convince
pragmatic knowledge engineers (KEs) since many successful expert
systems have been built for theoretically intractable NP-hard
problems. In this paper we motivate conceptual modeling restrictions
using pragmatic criteria such as KB-testability and
KB-maintainability. If such pragmatic criteria are ignored then, in
the usual case if certain restrictions are not enforced then
something important will stop working.
This article will be structured as follows. Firstly, we introduce
this work with some notes on defining evaluation criteria for an
expert system. This work is novel in the KBS community in that it
proposes to use an end-life cycle criteria of testability and
maintainability for early life cycle assessment. Next, the significance of
this work is discussed. The conventional structure preserving view
will be challenged. Suppose
a system is matured
via watching it run. Limitations to system
execution will hence effect how well the system can be matured. The
standard complexity analysis work from knowledge engineering will then
be reviewed. Such theoretical worst-case predictions of runtime, it
will be argued, are not not sufficient reason to restrict the modeling
process. However, recent work in the satisfiability community (an
experimental variant of the complexity community) has shown that
seemingly small variations in a theory can have immense implications
for the practicality of certain tasks. For example, it will be shown
that small changes in the size or fanout of the dependency graph of a
knowledge base can effectively block KB-testability. Such topological
limits, it will be argued, are unsatisfying for pragmatic knowledge
engineers. Topological limits can only be assessed once the knowledge
base has been built. A better approach would be to define modeling
languages in which no theory can run into trouble. The rest of the
article searches for language restrictions that guaranteed adequate
KB-testability and KB-maintainability. It turns out that the purpose
of the KB has impact on the restrictions. For example, certain
restrictions are only valid for KBs used in long simulation runs. In
the case of non-simulation systems, other restrictions apply.
An expert system passes through many stages in its life cycle. This
section argues that evaluation criteria for early-stage expert systems
can be defined via a consideration of late-stage functionality.
When we review the the life cycle of an expert system [Gaschnig et al., 1983], we
see that empirical evaluations are not possible for all points in the
life cycle. Gashing et.al. describes those stages are:

Researchers often stop at steps 1 or 2. Examples of reports from 3 are
not uncommon (e.g. [Schreiber & Birmingham, 1996, Menzies et al., 1992]). Stage 4 reports are
much less common (e.g. [Corbridge et al., 1995]) since this stage requires the
earlier work. There are very few examples of stage 5 reports
(exceptions include [Hori & Yoshida, 1997]) or higher, but some exist
(e.g. [McDermott, 1993]). As we progress through these stages, it gets
harder to isolate conflating effects. For example, [Hori & Yoshida, 1997]
reports benefits from using two techniques: problem solving methods
and an object-oriented reuse technique called design
patterns [Menzies, 1998]. It is hard to evaluate which of these
contributed to the reported benefits.
One useful technique when evaluating at stage 4 is to define
experiments using knowledge of how the system will be used in the
latter stages. Suppose we can build a detailed model of some
functionality desired at stage 8. Then, at stage 4, design variants
can be assessed by how they impact on the desired stage 8 functions.
In this article, we develop succinct computational models for two
stage 8 activities:
testing and maintenance.
This paper has two audiences. KR researchers may be unfamiliar with
model-based KA. KA audiences may be unfamiliar with the expressibility
vs tractability research in KR. This section discusses conceptual
modeling in KA. The next section discusses tractability research in
KR.
Conventional KA wisdom
(e.g. [Wielinga et al., 1992, Shadbolt & O'Hara, 1997]) advocates a separation between conceptual and
design models. A conceptual model stores all requirements without
being contorted due to implementation considerations. Only in the
design model, says the conventional wisdom, are programmers permitted
to make any pragmatic compromises required to create a practical
implementation. This view assumes that there are no serious
impediments to converting the conceptual model to the design model;
i.e. structure preservation is possible. Structure preservation
permits simpler knowledge base (KB) validation since an expert can see
the connection of a KB back to their original
conceptualisation [van Harmelen & Aben, 1996].
In the case where a conceptual model is not be used directly for
computational purposes, we have no issue with the laissez faire
view of conventional KA. For example, in the KADS methodology
[Wielinga et al., 1992], only the expertise conceptual model is directly implemented.
Tansley and Hayball [Tansley & Hayball, 1993] list over two dozen such expertise
models including systematic diagnosis (localisation and causal
tracing), mixed mode diagnosis, verification, correlation, assessment,
monitoring, simple classification, heuristic classification,
systematic refinement, prediction, prediction of behaviour and values,
design (hierarchical and incremental), configuration(simple and
incremental) planning, and scheduling. Other KADS conceptual models
which are not directly implemented include the organisation model
describing how workers will be effected by the expert system, or the
application model which describes the project scope and external
constraints.
However, if operational characteristics of the working program are
ever used to revise the conceptual model, then computational issues
associated with that model become relevant. For example:
-
If any conceptual model is searched for conflicts
(e.g. during the integration of multiple viewpoints from different
experts), then computational issues associated with that model become
relevant. A case could be made for restrictions to the conceptual
model in order to permit effective conflict detection
during requirements analysis. Conceptual
models appropriate for conflict detection are discussed
in [Mylopoulos et al., 1992, Chung & Nixon, 1995].
-
Many real-world complex domains can only be understood via an
exploratory methodology. For example:
-
Menzies and Compton note that all the expert systems they have
ever studied in detail are poorly understood; e.g.
process control,
farm management, economic modeling, biochemical interpretation,
consumer lending, and model-based diagnosis [Menzies & Compton, 1997].
-
Software solutions to
many standard business
require extensive iterative development (e.g. [Jacobson et al., 1992]);
In exploratory approaches, experience with the running program
informs revisions to
this conceptual model. Limitations to testing and then changing
(maintaining) the running program can hence
effect the nature of those revisions.
A counter-argument to our case against laissez faire conceptual
modeling is as follows: if a domain really demands certain
conceptualisations, then the conceptual model must really contain
them. Our reply to this counter argument is that it critically depends
on a demonstration of a domain really needing those
conceptualisations. Such a demonstration would require (i) the
construction of systems with and without certain conceptualisations;
(ii) an assessment of those systems using some objective success
measure. Note that such a demonstration at least implies a test measure;
i.e. this test of conceptual modeling may be only practical if the
conceptual model do not violate our limits to KB-testability.
This section argues that theoretical worst-case behaviour is
not a sufficient reason to restrict the modeling process. Practical KEs
prefer pragmatic criteria: i.e. a demonstration that in the
usual
case, something important will stop working (e.g. we lose KB-testability and
KB-maintainability)
unless we impose
restrictions.
This section discusses
analogous results from the knowledge representation (KR) community.
Some of these results are based on a worst-case analysis.
Others use instance generators to create a large number of
representative problems. We argue that such worst-case
analyses are poor motivation for KB restrictions. Hence, we prefer
pragmatic criteria such as KB-testability and KB-maintainability
which reflect usual case behaviour. However, we
apply the technique of instance generators in subsequent
sections.
Expressibility vs tractability trade offs are discussed extensively in
the KR literature (e.g. [Levesque & Brachman, 1985]). Solutions to a class of
problems (the NP-hard problems) are known to have an exponential
upper-bound on their runtimes; i.e. may be intractable. Much of the
KR literature is concerned with finding restrictive cases in which a
representation can be shown to tractable; i.e. worst-case runtimes are
polynomial. For example:
-
Tambe, Newell, and Rosenbloom [Tambe et al., 1990, Tambe & Rosenbloom, 1994] discuss multiple
attributes in production rule conditions. Given an attribute test of
an object, if one a query to one attribute of that object can result
in multiple matches, then the time bound on matching a single rule can
be exponential. Multiple attributes can be detected using a simple
local syntactic test.
-
Brachman and Levesque [Brachman & Levesque, 1984]
discuss a seemingly minor variation to a frame-based language FL.
FL contains the RESTR construct which places restrictions on
valid slot values. At first glance, RESTR seems to reduce the
search space associated with processing that frame. However, Brachman
and Levesque prove that the exact opposite is true. A language without
RESTR (FL
 ) can test if some frame subsumes another frame in,
at most, polynomial time. However, the same test in FL has an upper
bound of exponential time; i.e. it may be too slow to be practical.
) can test if some frame subsumes another frame in,
at most, polynomial time. However, the same test in FL has an upper
bound of exponential time; i.e. it may be too slow to be practical.
Opponents of worst-case
complexity analysis argue that potentially intractable runtimes are
not sufficient reason to restrict our KR languages:
-
A recent workshop on comparing different terminological logics
highlighted two schools of thought [D. Fensel, 1997]. In the one camp
were proponents of some restrictions to terminological logics to
description logics which have well-understood
runtimes.
In the opposing camp were proponents of frame logics
which maximise expressive power in order to capture ontological
features that
are inexpressible in description logics.
-
It is sometimes possible to transform a KB such that the
complexity is reduced.
For example,
for time-critical processing (e.g. real time expert systems) it could
be argued that possibly exponential runtimes must be avoided. Tambe
et.al. have shown that production rule conditions that only use
unique attribute matching have a linear time bound on the matching
process for a single production
(in single
attribute conditions, a query to one attribute of that object can
result in only a single match). However, in practice, this may not be
an expressibility limit since it is possible to convert conditions to
unique attributes.
Tambe et.al. report that a manual translation of 450 production
rules for R1-SOAR from multiple to single attribute conditions took
only two days. Tambe et.al. also speculate that tools could be built
to fully automate the process. However,
note that KB transformation is not
a general method for removing NP-hard problems.
For example, we cannot transform of FL to FL
 while preserving the semantics of
RESTR.
while preserving the semantics of
RESTR.
If a problem is NP-hard, this does not necessarily imply that
real-world examples of that problem cannot execute. Many expert
systems tasks, while theoretically intractable, have proven to be
practical for many real-world situation. For example, in
we describe below an empirical demonstration that an
NP-hard problem is practical for a range of real-world theories.
Further, it may be that only a narrow range within some
space of theoretically hard problems are actually
slow in practice.
For example consider the instance generator studies of binary
constraint satisfaction problems:
-
A binary constraint satisfaction
problem (2CSP) is to search for
a set of state assignments to variables which do not violate
constraints [Gent et al., 1995, Smith, 1996].
-
A
2CSP problem can be characterised by the parameters (n,m,p1,p2) where
n is the number of variables; m is the number of states per
variable; p1 is the probability of a constraint existing between
variable
n.i and variable
n.j and p2 is the probability that, given p1, that
some pair of state assignments is illegal.
-
A 2CSP instance generator can build any number of examples
problems from the parameters (n,m,p1,p2).
-
If n,m,p1 are held constant,
then there is a small range of p2 in which the number of possible
solution falls to zero. In this phase transition area, the
cost of performing a 2CSP task spikes to very high values, before
falling away to very low values in the no-solutions zone. For
example, for (8,10,1.0,p2) problems where p2 is between
0 and 0.4, the median cost of a 2CSP task is roughly
constant. However, as
p2 moves from 0.4 to 0.5, the median cost rises rapidly
by an order
of magnitude before decaying exponentially [Smith, 1996].
Such phase transition zones have been observed in numerous problems
that, theoretically, have a exponential worst-case time
complexity [Cheeseman et al., 1991]. Cheeseman et.al. have argued that
this phase transition marks the zone of truly slow tasks within the
NP-hard problems. If the Cheeseman speculation is correct, then we
can ignore worst-case time complexity results if we could somehow
guarantee that our expert system tasks occur outside of the really
hard zones within theoretically hard problems.
Given the
current state-of-the-art, such guarantee can only be offered in terms
of problem size and only in specific cases. For example, while
KB-testability and KB-maintainability is NP-hard (shown later),
we show below that we can define precise
boundaries within which it is practical. Further, in a result
analogous to the above results from the satisfiability community,
seemingly trivial variants in the modeling language can make KB-testability
and KB-maintainability impractical.
This section argues that
KB-testability is one such pragmatic criteria. KB-testability is
then used to identify two topological limits: a size
limit and a connectivity limit.
In later sections,
KB-maintainability will be used to identify limits to temporal modeling
languages.
This section explains why we view KB-testability as a necessary
pragmatic criteria.
Modern KA theorists view KB creation as the
construction of inaccurate surrogates models of
reality [Davis et al., 1993, Wielinga et al., 1992]. Agnew, Ford and Hayes [Agnew et al., 1993]
comment that expert-knowledge is comprised of context-dependent,
personally constructed, highly functional but fallible abstractions.
Practioners confirm just how inaccurate KBs can be.
Silverman [Silverman, 1992] cautions that systematic biases in expert
preferences may result in incorrect/incomplete KBs.
Compton [Compton et al., 1989] reports expert systems in which there was
always one further important addition, one more significant and
essential change. Working systems can contain multiple undetected
errors. Preece and Shinghal [Preece & Shinghal, 1992] document five fielded
expert systems that contain numerous logical anomalies.
Myers [Myers, 1977] reports that 51 experienced programmers could
only ever find 5 of the 15 errors in a simple 63 line program, even
given unlimited time and access to the source code and the executable.
Potentially inaccurate and evolving theories must be validated, lest
they generate inappropriate output for certain circumstances. Testing
can only demonstrate the presence of bugs (never their absence) and so
must be repeated whenever new data is available or a program has
changed. That is, testing is an essential, on-going process
through-out the lifetime of a KB. If expressibility
blocks testability, then expressibility should be restricted.
Arguments such as the above motivated Feldman and Compton [Feldman et al., 1989b],
followed by Menzies and Compton [Menzies, 1995, Menzies & Compton, 1997], to develop a general
test framework called QMOD/HT4. This section describes KB-testability,
a simplified version of that framework.
A KB can be characterised as domain facts and a set of problem solving
methods. If we partially evaluate the problem solving methods over the
domain facts, we arrive at the search space which could be traversed
at runtime. This search space can be characterised as the tuple
(E,V,O,S) where E is a set of directed edges connecting the
vertices V of types and-vertex, or-vertex.
Or-vertices represent literals and are generated from objects
O with S mutually exclusive states (one vertex is generated
for each state of each object). This characterisation fits qualitative
theories such as QCM (where S=3: up, down, steady); propositional
rule bases (where S=2: true,false) and any first-order theory that
can be unfolded in a finite number of steps to a ground horn-clause
theory (where S=2: true,false). F denotes the fanout of the
graph formed by (E,V) (fanout is the number of edges touching a
vertex and is the ratio of edges to vertices).
KB-testability can be characterised as the construction of pathways
across E from output vertices back to known input vertices.
Pathways must satisfy four criteria. (1) Pathways across an
or-vertex must include at least one parent of that or. (2)
Pathways across an and-vertex must include all the parents of that
and. Pathways must (3) not contain loops and must (4) not contain
mutually exclusive states. If an output vertex can be so connected to
an input vertex, it is called an explicable output.
Pathway criteria number 4 makes this an NP-hard problem. Gabow
et.al. [Gabow et al., 1976] showed that finding a directed path across a directed
graph that has at most one of a set of forbidden pairs is NP-hard.
Such forbidden pairs are present in the above definition of
KB-testability; i.e. two mutually exclusive states S.i, S.j of
some object O. When implemented, KB-testability has been observed
to exhibit exponential runtimes [Menzies, 1995], as one would expect for an
NP-hard problem.
This section applies the KB-testability criteria to identify a size
restriction to the topology of a KB search space.
Despite being NP-hard, KB-testability is still a practical validation
algorithm for a sample of fielded expert systems and published
theories of neuroendocrinology (the study of nerves and
glands). To demonstrate this, a KB-testability instance
generator was constructed by Menzies [Menzies, 1996b] as follows:
-
Let graph.0 be
an and-or graph from a real-world theory with
baseline parameters
E.b, V.b, O.b, S.b.
-
Let AV(IN) and AV(OUT) be the average number of vertices
denoted as inputs and outputs respectively used
when generating proofs over graph.0.
-
Starting from the baseline,
use a mutator to
introduce an increment into one
of the parameters and generate graph.i.
-
Execute graph.i as follows. Randomly
select up to AV(IN) vertices to be inputs
and up to AV(OUT) different vertices to be outputs.
Call KB-testability with those inputs and outputs.
For these experiments:
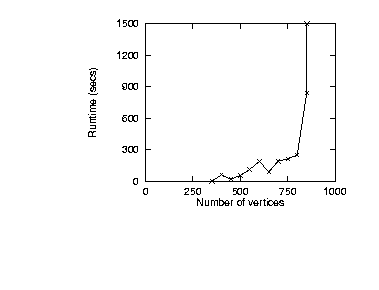
Note that an approximately linear increase in runtimes was noted up to
800 vertices. However, KB-testability did not terminate for theories
with more than 850 vertices
in under the give up time ( the vertical line in the
results). We conclude that the knee in the exponential runtime
curve kicks-in at around 800 vertices.
The claim the NP-hard process called KB-testability is valid for a
range of real-world theories relies on the observation that a sample
of real-world expert systems have less than 850 vertices.
This observation
comes from the verification community which collects the size of the
dependency graph between literals in fielded propositional expert
systems [Preece & Shinghal, 1992]
(see Table 1).
Application | vertices | fanout
-------------+-----------+-------
displan | 55 | 2
mmu | 65 | 7
tape | 80 | 4
neuron | 155 | 4
DMS-1 | 510 | 6
Table: Figures from a sample of fielded expert systems.
From [Preece & Shinghal, 1992].
These results suggests that a practical
KB-testability must work at least for between 55 to 510 vertices
and a fanout of 2 to 7. That is, KB-testability is practical for
real-world expert systems, despite being NP-hard.
In other demonstrations of its practicality, KB-testability
has been used to detect faults in theories of neuroendocrinology
published in international refereed journals (neuroendocrinology is
the study of nerves and glands). Feldman and Compton [Feldman et al., 1989a],
followed by Menzies and Compton [Menzies & Compton, 1997], have shown that
KB-testability could detect previously unseen errors in theories in
neuroendocrinology published in international refereed
journals. Interestingly, these faults were found using the data
published to support those theories.
This section applies the KB-testability criteria to identify a connectivity
restriction to the topology of a KB search space.
In other studies with QCM, another
instance generator (mutator.2)
was built for the Smythe '89 theory which
kept the number of vertices
(roughly) constant but added edges at random to produce new
graphs of larger fanouts. Six graphs were generated with
(449, 480, 487, 494, 511, 535) vertices.
Figure 2 shows
the results.
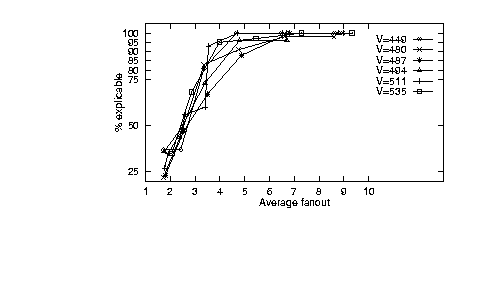
Figure: KB-testability explicables. From [Menzies, 1996b].
At low fanouts, many behaviours were
inexplicable. However, after a fanout of 4.4, most behaviours were
explicable. Further, after a fanout of 6.8, nearly all the behaviours
were explicable [Menzies, 1996b]. Hence, another KB-testability limit is that,
after a certain level of inter-connectivity, a theory is able to
reproduce any input/output pairs; i.e. it is not adequately
restrictive.
An unrestrictive inference procedure that condones
any behaviour at all from a theory is not a useful inference
procedure. After the point where the percent explicable approaches 100
percent,
KB-testability becomes a useless evaluation tool.
The previous section can be summarised as a pragmatic recommendation
of restricting KB topology
to medium-sized theories which are not highly
connected. A drawback with applying these limits is the
forbidden fruit problem
(the forbidden fruit is always the
sweetest and hence the most desirable). Suppose a KE has
invested considerable effort into certain assertions; e.g. they have
developed them over a long period of time or have successfully
defended them from all critics. If we tell such a KE that some
of these assertions are forbidden due to their undesirable properties
(e.g. possible exponential runtimes, phase transition problems,
limits-to-test problems), then the KE may still object to their
deletion.
More formally, Silverman notes that agents which criticise a KB can be
divided into influencers which block errors occurring and
debiasers
which fix errors after they occur [Silverman & Wenig, 1993].
Silverman has experimental results suggesting negative feedback
(i.e. the use of a debiasers) is almost always unsuitable, if only
used without positive feedback (influencers). The limits of the
previous section would be classed as debiasers since they can only act
after the KE has created a problematic KB.
A representation language in which it is impossible to make
pragmatically problematic assertions would act as a very strong
influencer to a KE. If a KE can't assert X, then they'll never have
a running example which is hindered after X is removed. The rest of
this article searches for any such pragmatic expressibility
restrictions within QCM.
Expressibility restrictions for KB-testability relate to the steady nodes in
QCM and asymmetrical causal connections. Asymmetric causal
connections do not comment on the connection of all upstream states to
all downstream state. Steady nodes are implemented via
and-vertices that combine the influence of two competing upstream
parents down to a steady vertex. It will be found that if we intend
to use QCM for very long simulation runs, then we need to forbid
both these constructs.
Expressibility restrictions for KB-maintainability relate to temporal
causal connections. In a qualitative language, if we say that
(e.g.) X encourages Y (denoted
X++Y), it is under-specified
how long it takes for the X influence to effect Y.
It will be found that different interpretations of this time delay
have a significant effect on maintainability.
This section observes that the presence of conjunctions improves the
testability of a theory. However, this conclusion only applies to
theories not used to generate time-series data. It will be shown
later that KBs used for such simulation purposes should avoid
conjunctions.
One observation made in the above changing fanout study
was that runtimes varied widely as the fanout was increased.
To explore this further, we built new instance generators
(mutator.3, mutator.4a, mutator.4o)
which kept
the number of vertices, AV(IN) and AV(OUT) constant while varying
the fanout. In all, 155 graphs were generated and executed 2513
times
(see Table 2).
| Generated | Number
| graphs | of runs
------------------------------------------+-----------+--------
mutator.3 : basic changing fanout study | 76 | 1597
mutator.4a : changing fanout, ands only | 42 | 483
mutator.4o : changing fanout, ors only | 37 | 433
------------------------------------------+-----------+--------
Totals | 155 | 2513
Table 2: Number of experiments with mutating fanout.
Mutator.3 worked as follows.
Starting with the and-or graph from
Smythe '89, edges were added at random
till some desired fanout was reached.
The runtimes of mutator.3 seemed independent of
fanout.
It was hypothesised that
the observations of mutator.3
was displaying more than one effect. Hence, two
more studies were performed where (i) edges were only added upstream
to and-vertices (mutator.4a); (ii) edges were only added
upstream to or-vertices (mutator.4o). Note that in both
mutator.4a and mutator.4o, the number
of vertices, AV(IN) and AV(OUT) were
kept constant.
The runtimes of mutator.4a were observed to always be less than
or equal to mutator.4o
(see Figure 3).
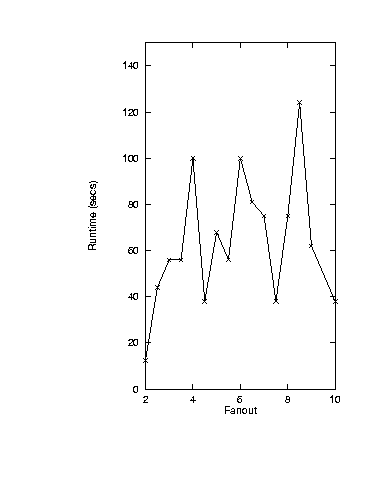
A. Mutator.3 runtimes
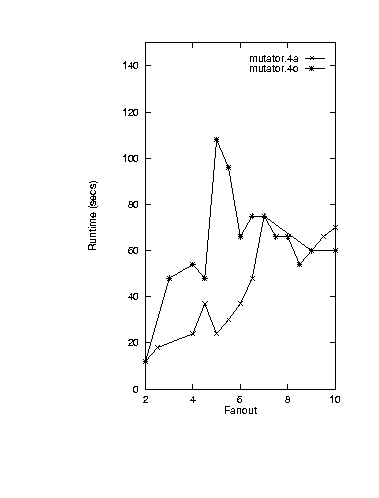
B. Mutator.4a and mutator.4o runtimes
Figure 3: KB-testability runtimes.
We
hypothesis that adding edges upstream of an and vertex increases
the constraints on proof generation over that vertex (i.e. more
pre-conditions need to be satisfied). Roughly speaking, adding
ands adds constraints making it more likely that proof generation
will terminate earlier.
We conclude that for KB-testability, conjunction adds constraints
which restricts inferencing and decreases the associated runtimes.
Hence, for the purposes of KB-testability, the creation of
theories with numerous conjunctions should be encouraged.
This section shows that for very long simulation runs, conjunctions
make KB-testability
impractical. The next section argues that for simulations of
any length of time, other small variants in a language can make
KB-maintainability impractical.
The study in the previous section assumed the basic KB-testability
constraint; i.e. no object can be
assigned
more than one state.
In several commonly used KBS representations, this assumption
is not valid since objects can be assigned
several states of the lifetime of a simulation:
-
Rule-bases that
are processed via a standard match-select-act loop may assert and
retract facts many times during its processing;
-
As the inference
executes over loops in qualitative theories or topoi
graphs (topoi graphs depict statements of gradual knowledge
such as the more this, the less that [Dieng et al., 1995]),
literals may be assigned different belief
values at different times.
We use the term KB-time-testability to
denote the KB-testability variant in which
the
belief values of literals can change during a simulation. The rest of
this section explores limits to KB-time-testability.
One approach to KB-time-testability would be to create one copy of the search
space for each time interval in the simulation. For example,
consider the theory
A encourages B but B discourages A.
In QCM, this is denoted A++B and B-A where
++ and - are
QCM
causal connections. X++Y
means that Y being up or down could be explained by
X being up or down respectively.
X-Y
means that Y being up or down could be explained by
X being down or up respectively.
If we executed A++B and B-A over three time ticks, we could
search the space
shown in Figure 4.
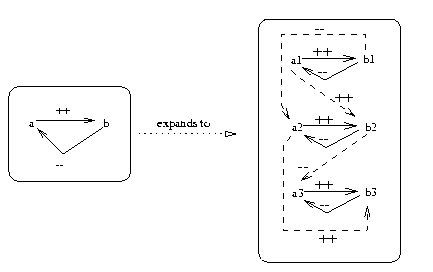
Figure 4: A theory (left) renamed over 3 time intervals and connected
using IEDGE (time edges shown as dashed edges).
Here we are connecting objects at different time
intervals by an implicit time edge linking
or IEDGE policy: when
i.e. X++Y implies that
X at time T=i
also connects to Y at T=i+1 (see the dashed lines).
Alternatives to IEDGE are discussed later in the
discussion
on KB-maintainability.
The advantage of this approach is that we could use the QCM inference
procedures (e.g. KB-testability) for testing time-based simulations.
The disadvantage of this approach is that the graph size would
increase linearly with the number of copies. Recall that,
experimentally, KB-testability has been observed to exhibit the
exponential runtimes. Hence, long simulation runs are not
KB-time-testability in this manner.
Note that each time copy repeats some structure for the known time
intervals in the simulation. A compelling intuition is that no
explanation path can be found through T+1 copies that can't be found
in T copies. If this were true, then we could reduce the search
space of KB-testability by not copying the structure at
all. Menzies and Cohen [Menzies & Cohen, 1997] show that this optimisation
is not possible if we allow asymmetric edges in our theories.
X++Y and X-Y
are examples of
symmetric causal edges
in that they make some statement about every state of
the downstream vertex Y.
X+-+Y is an example of an
asymmetric causal edge: Y being up could be explained by X
being up but not visa versa.
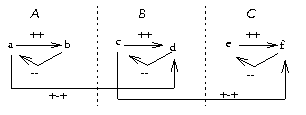
Figure 5: A theory with asymmetric edges
from a to d and from
c to f.
For example, Figure 5
contains
two asymmetric causal edges ( A+-+D;
C+-+F) which expands into the
graph
of Figure 6.
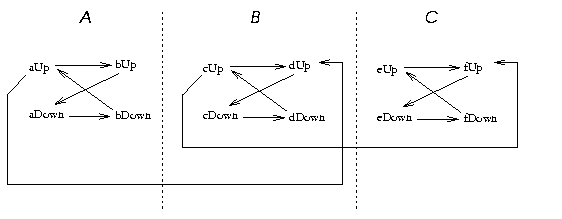
Figure: The graph within Figure 5.
This figure
duplicates the topology of our above theory
in the regions A,B,C with an extra link from the
top-left vertex of one region to the top-right vertex of the next
region. A path from bUp to eUp will take at 3 time
intervals to cross from top-left to top-right in each of the regions
A,B,C. By repeating A,B,C more times, we can generate
dependency graphs which would require any number of intermediaries to
traverse. This example suggests that between each measured time
interval we may need many intermediary copies.
We have shown elsewhere [Menzies et al., 1997] that for theories whose variables
take only S states and which lack asymmetric edges and which are
connected
via IEDGE, then if we can't
generate a proof in S copies, then we will never be able to generate
a proof at all. Roughly speaking, if every edge offers a comment on
all the states of its downstream vertices (i.e. they are symmetric),
then the state space rapidly saturates and we can reduce the
granularity of the time axis to just under twice the granularity of
the measurements of that theory. We can use this proof as an
optimisation technique as follows.
Suppose, for example, that:
-
We had a S=2-state device with symmetric edges which has been
running for a million time steps.
-
We only collected measurements at three time points (say,
1 and 500,000 and 1,000,000.
If we had not proved saturation for our device, then the search for
these proofs would have to explore 1,000,000 renamings. Given the
exponential runtimes of KB-testability, this is clearly undesirable.
However, since we have proved saturation, then we know that if a proof
cannot be found in two renamings, then no such proof exists. Consider
a proof from (e.g.) time 1 to time 500,000. If that proof cannot
terminate in the space 1 and 500,000, then it will never
terminate. That is, when building this proof, we could ignore the
search space that used the renamings from 2 to 499,999. A similar
argument could be made for proofs from 500,000 to 1,000,000. In
practice, we would only need to search the space created for the three
measured time points. That is, in this example, this optimisation
lets us reduce the search space to three-millionths of the unoptimised
version. More generally, if an S state device which supports
saturation is run for T1 time ticks, and if we only measure this
theory at T2 time intervals, then we can reduce the search space
by a factor of T2/T1. In the case where T2 is very much
smaller than T1, then this is a significant reduction in the
search space.
Recall that in QCM, conjunction is used to conceptualise explanations
of steady values (a conjunction of two competing upstream influences
can cancel each other out). We now demonstrate by counter-example
that conjunction blocks saturation. That is, if we add conjunction to
bi-state devices connected by symmetric edges, then we need an
unbounded number of copies in order to perform KB-time-testability.
Note that this rejection of conjunction implies that we can't execute
steadies in a QCM theory.
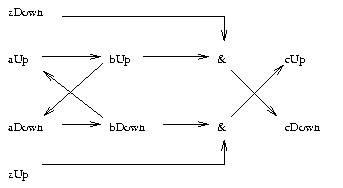
Figure 7: An example graph.
A minimum of three time
intervals are required to
explain cUp in terms of set
(aUp, zUp)
Consider the graph in Figure 7.
Three time intervals are
required to explain cUp in terms of (aUp,zUp). In
the first time interval we explain (aUp,bUp,zUp). In
the second time interval we explain (aDown,bUp,zUp).
In the third time interval we explain (bDown,zUp), and by
conjunction, cUp.
We create our counter-example by connecting duplicates of this graph
as demonstrated
in Figure 8.
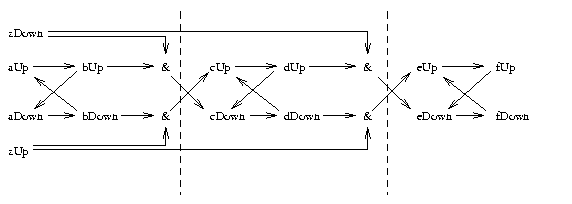
Figure 8: An example of the construction of our
counter-example. In this case, a minimum of 7 time intervals is
required to explain ``fUp'' in terms of ``(aUp,zUp)''.
In this figure a minimum of 7 time intervals is required to explain
fDown in terms of (aUp,zUp). It is easy to show that in
general, with D duplicates connected in this manner, the maximum
number of time intervals to perform an explanation is at least
2D+1, which is not a constant. This contradicts our previous
result for the case of symmetric edges without conjunctions (i.e. 2
time intervals were enough for explanation).
We conclude that long simulation runs is not KB-time-testability if the
theory includes conjunction. Note that short simulation runs of
theories with conjunction is still be KB-testability if we (i) ignoring the
symmetric edges optimisation; (ii) creating one copy for each time
tick. However, for long simulation runs, we
recommend using a QCM variant
formed by removing conjunction (and hence steadies)
and the asymmetric causal edges.
This section describe KB-maintainability, an extension to
KB-testability.
If will be shown that seemingly minor variants in a language
can severely
impact on the practicality of KB-maintainability.
Given we can test a theory, what kind of results assist in
maintaining that theory? One requirement would be the ability to check if
some variation of a theory is better than the original theory.
We can use this requirement to define
a comparative measure of KB-maintainability.
Given
a theory Ti
written in two languages. As we revise our theory, we
generate T1, T2, T3.... Given the
above test procedure, we can
assess if some theory Ti is better than another theory Tj.
According to the KB-maintainability
requirement, language one will be
considered better than language two if:
- In language one
we can check that Ti is better than Tj;
- But in language two, we cannot.
We can apply this definition experimentally as follows.
Given a range of models ranked from good to poor,
we like to see the maintenance success curve
of Figure 9.
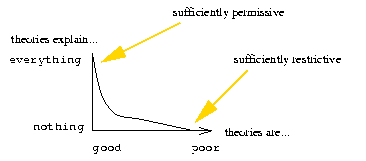
Figure 9: Visualising a maintainable representation language.
The KB-testability curve of a good representation
should be both permissive to all good
theories (explains correct
behaviour) and restrictive to all bad theories (prevent poor theories
explaining any behaviour).
A good theory is permissive; i.e. it can explain known behaviour
(the success curve rises high on the left-had-side). However, we also
need to test that the permissiveness is not due to a
poorly-constrained theory. A theory that condones any conclusion is a
poor theory. Hence, a theory must also be restrictive (the success
curve descents to a low value on the right-hand-side). Further, we
want the second derivative of this graph to be non-negative; e.g. the
ski-slope shape of success curve. With such a curve, we can quickly
get feedback if some change improves or degrades a theory.
We say that a representation is KB-maintainability if its
KB-testability curve for good to bad theories looks like the ski-slope
of the success curve. We show below that only some representations of
time in QCM satisfy this definition of KB-maintainability. Hence, in
QCM, conceptual modeling should be restricted to these representations
of time. Note that KB-maintainability uses KB-testability as a
sub-routine; i.e. KB-maintainability is NP-hard since KB-testability
is also NP-hard.
How can time be represented in QCM? We saw above the use of
IEDGE: when X connects to Y, then we say
that X at time T=i also connects to Y at T=i+1.
IEDGE is only one of a family of temporal QCM
languages.
Firstly, we can cross time over edges
or over nodes. Secondly, we can cross time on all structures in the
theory, or only on those explictedly mentioned by the user. Each
combination of these alternatives defines a new temporal modeling
language, illustrated
in Figure 10.
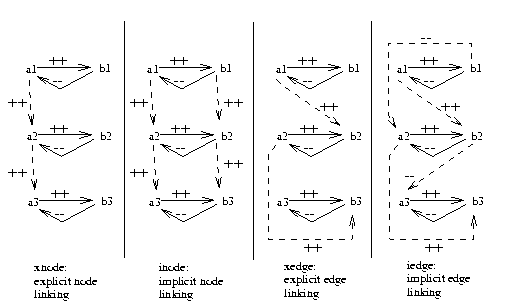
Figure: Figure 4 (left) renamed over 3 time intervals using
different
time linking methods.
Dashed lines indicate time edges.
In this figure, in the explicit node linking language (or
XNODE), we only cross time on the nodes explicitly denoted as
time nodes by the user (in this example, A). In the
implicit node linking language (or INODE), we cross time on all
nodes. In the explicit edge linking language (or XEDGE),
we only cross time on the edges explicitly denoted as time edges by the
user (in this example, A to B). Lastly, in
IEDGE, we cross time on all edges.
To test KB-maintainability for these four temporal languages, we performed the
following experiment. First, we implemented a quantitative
fisheries simulation model using the equations
from [Bossel, 1994] (pages 135-141). Secondly, we built a qualitative form
of the fisheries model as shown
in Figure 11.
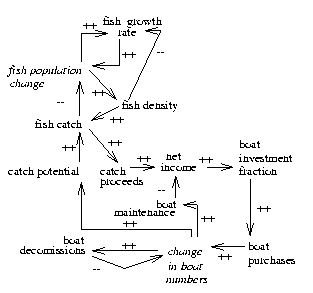
Figure: The fisheries model. Adapted
from [Bossel, 1994] (pp135-141).
Variables in italics were used in the XNODE
study. Edges downstream of an XNODE were used as the
explicit time edges in the XEDGE language.
The quantitative model
was used to generate numeric test data which was stored in the
measure array. From each comparison of measure(i) with
measure(j), entries were written to an array of qualitative
observations called changes. Changes was used to generate
the input/output needed for for KB-testability. For example, if in comparison
change(37), the fish density fdens was increased and the
fish catch fcatch was always seen to decrease at all time steps,
then change(37).in is (fdensUp) and
change(37).out is (fcatch(t=1)Down, fcatch(t=2)Down,
fcatch(t=3)Down, fcatch(t=4)Down, fcatch(t=5)Down)
Next, we built mutator.5 as follows: the sign on a random sample of
the X statements in the qualitative theory were corrupted:
i.e. flipped (++ to - or visa versa). Given a model
with E edges, then as we vary X from 0 to E, we are
moving from a good model to a poor model; i.e. the x-axis
of our maintenance success curve.
This corrupted model was then copied to create a set
of time copies. These time copies were connected using one
of our temporal languages: IEDGE, INODE, XEDGE,
XNODE. Change inputs were mapped into copy(0).
Change outputs were mapped into some copy(i) (i greater
than zero). The
success of each run was assessed by
recording the percent of the explicable outputs i.e. those outputs
that the model could connect back to inputs.
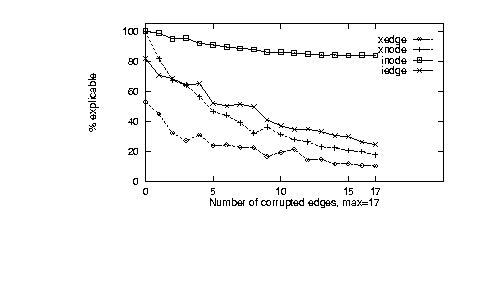
Figure 12: Graph of Xplicable.
Figure 12
graphs the average values of Xplicable variable from the experimental
design. INODE was not sufficiently restrictive.
Even with all edges corrupted, INODE allowed theories to
explain correct behaviour. Also, XEDGE was not sufficient
permissive. Even on correct theories, XEDGE could only explain
half the known behaviour. XNODE was the closest to the
maintenance success curve, followed by IEDGE. However,
IEDGE was not as permissive as XNODE. Hence, except in
the case where we need to optimise long simulation runs, we recommend
XNODE. Otherwise, we recommend IEDGE.
Note that for XNODE and IEDGE, after only a third of the
theory being mutated, only half the outputs were inexplicable.
This is a nice result: with these modeling languages,
we can get a clear and early indication if we are
stray from a good theory.
We conclude that, in terms of KB-maintainability, the four variants on the QCM
conceptual modeling language are ranked: XNODE (best for short
to medium length
simulation runs), then IEDGE (best for long simulation runs),
then XEDGE (poor: no permissive enough) and INODE (poor:
not restrictive enough).
If there are no blocks to structure preservation, then our
conceptual modeling need not be restricted. Unrestricted conceptual
modeling requires that we can structurally preserve
conceptual structures.
If structure preservation is blocked by certain features
of a conceptual modeling language,
then if we use those features,
our implementation may be compromised.
In order to identify such blocks to structure preservation, we need to
first identify pragmatic success criteria for our KBs. Such pragmatic
success criteria should reflect functionality that we will require, in
the usual case. Worst-case time complexity analysis is not such a
pragmatic criteria. However, KB-testability and KB-maintainability
are pragmatic criteria since
checking and revising
a theory is so important when performing KA
(construction inaccurate surrogates
of reality). Topological restrictions were
found via KB-testability:
-
Size restrictions;
-
Connectivity restrictions;
For none-time-based simulations, the use of conjunctions was observed
to improve
KB-testability.
In the case where the conceptual model will be
used for time-based simulation runs, expressibility restrictions were found
via KB-time-testability and KB-maintainability:
-
No conjunctions;
-
No steadies;
-
No asymmetric causal connections;
-
Avoid XEDGE or INODE temporal connections.
We have hence shown that there are cases where it is necessary to
restrict a conceptual modeling language. That is, there
exists conceptual knowledge that we just should not add to our KBs.
This belief runs counter to the standard wisdom in the KA community;
i.e. design and implementation considerations should not contort the
high-level descriptions of an expert's conceptual knowledge. The
techniques we used (KB-testability, KB-maintainability, instance generators, graph theory)
represent a general evaluation methodology and could be applied to
many other theories and representations.
References
- Agnew et al., 1993
-
Agnew, N., Ford, K., & Hayes, P. (1993).
Expertise in Context: Personally Constructed, Socially elected, and
Reality-Relevant?
International Journal of Expert Systems, 7.
- Benjamins & Aben, 1997
-
Benjamins, R. & Aben, M. (1997).
Structure-Preserving Knowledge-Based Systems Development Thorugh
Reusable Libraries: A Case Study in Diagnosis.
International Journal of Human-Computer Studies, 47:259-288.
- Booch, 1994
-
Booch, G. (1994).
Object-Oriented Design with Applications (second
edition).
Benjamin/ Cummings.
- Bossel, 1994
-
Bossel, H. (1994).
Modeling and Simulations.
A.K. Peters Ltd.
ISBN 1-56881-033-4.
- Brachman & Levesque, 1984
-
Brachman, R. & Levesque, H. (1984).
The Tractability of Subsumption in Frame-Based Description Languages.
In AAAI '84, pages 34-37.
- Cheeseman et al., 1991
-
Cheeseman, P., Kanefsky, B., & Taylor, W. (1991).
Where the Really Hard Problems Are.
In Proceedings of IJCAI-91, pages 331-337.
- Chung & Nixon, 1995
-
Chung, L. & Nixon, B. (1995).
Dealing with Non-Functional Requirements: Three Experimental Studies
of a Process-Oriented Approach.
In Proceedings of ICSE '95: the International Conference on
Software Engineering, pages 25-36.
- Compton et al., 1989
-
Compton, P., Horn, K., Quinlan, J., & Lazarus, L. (1989).
Maintaining an Expert System.
In Quinlan, J., (Ed.), Applications of Expert Systems,
pages 366-385. Addison Wesley.
- Corbridge et al., 1995
-
Corbridge, C., Major, N., & Shadbolt, N. (1995).
Models Exposed: An Empirical Study.
In Proceedings of the 9th AAAI-Sponsored Banff Knowledge
Acquisition for Knowledge Based Systems.
- D. Fensel, 1997
-
D. Fensel, M.-C. Rousset, S. D. (1997).
Workshop on Comparing Description and Frame Logics.
to appear in Data and Knowledge Engineering.
http://www.aifb.uni-karlsruhe.de/WBS/dfe/dlfl/summary.html.
- Davis et al., 1993
-
Davis, R., Shrobe, H., & Szolovits, P. (1993).
What is a Knowledge Representation?
AI Magazine, pages 17-33.
- Dieng et al., 1995
-
Dieng, R., Corby, O., & Lapalut, S. (1995).
Acquisition and Exploitation of Gradual Knowledge.
International Journal of Human-Computer Studies, 42:465-499.
- Feldman et al., 1989a
-
Feldman, B., Compton, P., & Smythe, G. (1989a).
Hypothesis Testing: an Appropriate Task for Knowledge-Based
Systems.
In 4th AAAI-Sponsored Knowledge Acquisition for
Knowledge-based Systems Workshop Banff, Canada.
- Feldman et al., 1989b
-
Feldman, B., Compton, P., & Smythe, G. (1989b).
Towards Hypothesis Testing: JUSTIN, Prototype System
Using Justification in Context.
In Proceedings of the Joint Australian Conference on Artificial
Intelligence, AI '89, pages 319-331.
- Gabow et al., 1976
-
Gabow, H., Maheshwari, S., & Osterweil, L. (1976).
On Two Problems in the Generation of Program Test Paths.
IEEE Trans. Software Engrg, SE-2:227-231.
- Gaschnig et al., 1983
-
Gaschnig, J., Klahr, P., Pople, H., Shortliffe, E., & Terry, A. (1983).
Evaluation of Expert Systems: Issues and Case Studies.
In Hayes-Roth, F., Waterman, D., & Lenat, D., (Eds.),
Building Expert Systems, chapter 8, pages 241-280. Addison-Wesley.
- Gent et al., 1995
-
Gent, I., MacIntyre, E., Prosser, P., & Walsh, T. (1995).
Scaling Effects in CSP Phase Transistion.
In International Conference on Principles and Practice of
Constraint Programming.
- Hori & Yoshida, 1997
-
Hori, M. & Yoshida, T. (1997).
Domain-oriented library of scheduling methods: Design Principle and
real-life application.
In Workshop on Problem-Solving Methods for Knowledge-based
Systems, IJCAI '97, August 23.
- Jacobson et al., 1992
-
Jacobson, I., Christerson, M., Jonsson, P., & Overgaard, G. (1992).
Object-Oriented Software Engineering: A Use Case Driven
Approach.
Addison-Wesley.
- Levesque & Brachman, 1985
-
Levesque, H. & Brachman, R. (1985).
A Fundamental Tradeoff in Knowledge Representation and Reasoning
(Revised Version).
In Brachmann, R. & Levesque, H., (Eds.), Readings in
Knowledge Representation, pages 41-70. Palo Alto, Morgan Kaufmann.
- McDermott, 1993
-
McDermott, J. (1993).
R1 ("XCON") at age 12: lessons from an elementary school achiever.
Artificial Intelligence, 59:241-247.
- Menzies, 1995
-
Menzies, T. (1995).
Principles for Generalised Testing of Knowledge Bases.
PhD thesis, University of New South Wales. Avaliable from
http://www.cse.unsw.edu.au/ timm/pub/docs/95thesis.ps.gz.
- Menzies, 1996b
-
Menzies, T. (1996b).
On the Practicality of Abductive Validation.
In ECAI '96.
Available from
http://www.cse.unsw.edu.au/ timm/pub/docs/96abvalid.ps.gz.
- Menzies, 1997
-
Menzies, T. (1997).
Evaluation Issues for Problem Solving Methods.
Banff KA workshop, 1998. Available from
http://www.cse.unsw.edu.au/ timm/pub/docs/97eval.
- Menzies, 1998
-
Menzies, T. (1998).
OO Patterns: Lessons from Expert Systems.
Software Practice & Experience.
In press. Available from
http://www.cse.unsw.edu.au/ timm/pub/docs/97probspatt.ps.gz.
- Menzies, 1996a
-
Menzies, T. (September, 1996a).
Applications of Abduction: Knowledge Level Modeling.
International Journal of Human Computer Studies, 45:305-355.
Available from
http://www.cse.unsw.edu.au/ timm/pub/docs/96abkl1.ps.gz.
- Menzies et al., 1992
-
Menzies, T., Black, J., Fleming, J., & Dean, M. (1992).
An Expert System for Raising Pigs.
In The first Conference on Practical Applications of Prolog.
Available from
http://www.cse.unsw.EDU.AU/ timm/pub/docs/ukapril92.ps.gz.
- Menzies & Cohen, 1997
-
Menzies, T. & Cohen, R. (1997).
A Graph-Theoretic Optimisation of Temporal Abductive Validation.
In European Symposium on the Validation and Verification of
Knowledge Based Systems, Leuven, Belgium.
Available from
http://www.cse.unsw.edu.au/ timm/pub/docs/97eurovav.ps.gz.
- Menzies et al., 1997
-
Menzies, T., Cohen, R., S, W., & Goss, S. (1997).
Applications of Abduction: Testing Very Long Qualitative Simulations.
Submitted to IEEE Transactions of Data and Knowledge Engineering.
Available from http://www.cse.unsw.edu.au/ timm/pub/docs/97iedge.ps.gz.
- Menzies & Compton, 1997
-
Menzies, T. & Compton, P. (1997).
Applications of Abduction: Hypothesis Testing of
Neuroendocrinological Qualitative Compartmental Models.
Artificial Intelligence in Medicine, 10:145-175.
Available from
http://www.cse.unsw.edu.au/ timm/pub/docs/96aim.ps.gz.
- Myers, 1977
-
Myers, G. (1977).
A Controlled Experiment in Program Testing and Code
Walkthroughs/Inspections.
Communications of the ACM, 21:760-768.
- Mylopoulos et al., 1992
-
Mylopoulos, J., Chung, L., & Nixon, B. (1992).
Representing and Using Nonfunctional Requirements: A Process-Oriented
Approach.
IEEE Transactions of Software Engineering, 18(6):483-497.
- Preece & Shinghal, 1992
-
Preece, A. & Shinghal, R. (1992).
Verifying Knowledge Bases by Anomaly Detection: An Experience Report.
In ECAI '92.
- Schreiber & Birmingham, 1996
-
Schreiber, A. T. & Birmingham, W. P. (1996).
The Sisyphus-VT initiative.
International Journal of Human-Computer Studies, 44(3/4).
- Shadbolt & O'Hara, 1997
-
Shadbolt, N. & O'Hara, K. (1997).
Model-based Expert Systems and the Explanations of Expertise.
In Feltovich, P., Ford, K., & Hoffman, R., (Eds.),
Expertise in Context, chapter 13, pages 315-337. MIT PRess.
- Silverman, 1992
-
Silverman, B. (1992).
Survey of Expert Critiquing Systems: Practical and Theoretical
Frontiers.
Communications of the ACM, 35:106-127.
- Silverman & Wenig, 1993
-
Silverman, B. & Wenig, R. (1993).
Engineering Expert Critics for Cooperative Systems.
The Knowledge Engineering Review, 8(4):309-328.
- Smith, 1996
-
Smith, B. (1996).
Locating the Phase Transition in Binary Constraint Satisfaction
Problems.
Artificial Intelligence.
- Smythe, 1989
-
Smythe, G. (1989).
Brain-hypothalmus, Pituitary and the Endocrine Pancreas.
The Endocrine Pancreas.
- Tambe et al., 1990
-
Tambe, M., Newell, A., & Rosenbloom, P. (1990).
The Problem of Expensive Chunks and its Solution by Restricting
Expressiveness.
Machine Learning, 5(3):299-348.
- Tambe & Rosenbloom, 1994
-
Tambe, M. & Rosenbloom, P. (1994).
Investigating Production System Representations for Non-combinatorial
Match.
Artificial Intelligence, 68(1).
- Tansley & Hayball, 1993
-
Tansley, D. & Hayball, C. (1993).
Knowledge-Based Systems Analysis and Design.
Prentice-Hall.
- van Harmelen & Aben, 1996
-
van Harmelen, F. & Aben, M. (1996).
Structure-Preserving Specification Languages for Knowledge-Based
Systems.
International Journal of Human-Computer Studies, 44:187-212.
- Waugh et al., 1997
-
Waugh, S., Menzies, T., & Goss, S. (1997).
Evaluating a Qualitative Reasoner.
In Sattar, A., (Ed.), Advanced Topics in Artificial
Intelligence: 10th Australian Joint Conference on AI. Springer-Verlag.
- Wielinga et al., 1992
-
Wielinga, B., Schreiber, A., & Breuker, J. (1992).
KADS: a Modeling Approach to Knowledge Engineering.
Knowledge Acquisition, 4:1-162.