Abstract: While diagnostic problem solving is in principle well understood, building and maintaining systems in large domains cost effectively is an open issue. Various methods have different advantages and disadvantages making their integration attractive. When switching from one method to another in an integrated system, as much knowledge as possible should be reused. We present an inference structure for diagnostic problem solving optimized with respect to knowledge reuse among methods motivated by experience from large knowledge bases built in medical, technical and other diagnostic domains.

1. Introduction

Diagnostic Problem Solving probably is the best understood subdomain of knowledge (expert) systems [Puppe 93, Breuker & Velde 94]. Diagnostic (classification) problems can be characterized as the selection of solutions from a preenumerated set of alternatives (diagnoses) for a problem described by observations (symptoms). Typical domain types (see [Puppe 93, chap. 13.2]) are medical diagnosis and therapy selection, object identification (e.g. plants, rocks), fault finding for technical devices and processes (e.g. car engines, printing machines), assessment (e.g. credit granting or legal advice) and precedence selection (e.g. looking for the best product). There are a variety of successful problem solving methods for categorical, heuristic, causal or case-oriented knowledge requiring different representations ([Puppe 96]; for variants not mentioned here, see e.g. [Benjamins 95]):

• Categorical classification using decision trees or decision tables
• Heuristic classification using knowledge of the kind "if <symptoms> then <diagnoses> with <evidence>, the latter estimated by experts. Diagnoses are rated according to their accumulated evidence.
• Causal Classification with various kinds of models:
  • Set covering classification using knowledge of the kind "if <diagnosis> then <symptoms> with <frequency>", the latter estimated by experts. Diagnoses are rated according how well they cover (explain) the observed symptoms.
  • Functional classification using a system model with abstract "components" and "materials". (Abnormal) Symptoms are calculated as differences between expected and observed system behavior and diagnoses are local changes of the system model (usually a malfunction of components) capable of predicting the symptoms.
  • Behavioral classification, which is similar to functional classification but starts with a system model based on physical (behavioral) principles, where the intended function is just one of many behaviors of a structure.
• Case-oriented classification using cases as the primary knowledge source in different ways:
  • Statistical classification using knowledge about the a priori probability of diagnoses P(D) and the conditional probability P(S/D) of symptom S if diagnosis D is present, where the probabilities are calculated from a representative case base. Diagnoses are rated according to the Theorem of Bayes or with Bayesian nets.
  • Neural classification using a case base for adapting the weights of a neural net capable of classifying new cases.
  • Case based classification using a case base directly together with knowledge about a similarity measure. For a new case, the most similar cases from the case base are selected assuming their solutions (diagnoses) to be applicable to the new case as well.

At least in principal, all methods can be applied to all classification domains with one important exception: Functional and behavioral classification are only applicable for fault finding (troubleshooting) by searching for differences between the correct and a malfunction of a system. Classification domain types without such a model are e.g. object identification, assessment and precedence selection (see above).

While the principal problems of diagnostic modeling are quite well understood, and for most domains routine approaches can be offered, the cost effectiveness of large knowledge bases (with more than 1000 symptoms and diagnoses) is a major issue. For a company, the crucial question is whether the expected benefits from routine use exceeds the costs incurred from building and maintaining the knowledge base. Since the knowledge acquisition costs increase exponentially with the degree of completeness of knowledge bases, we cannot make the assumption [Fensel & Benjamins 96, van Harmeln & ten Teije 98], that knowledge bases are complete - neither with respect to the coverage of all possibly relevant observations nor with respect to the correctness and completeness of the knowledge drawing conclusions from them. In the following we concentrate on interactive systems with the user entering at least some of the symptoms of the case (as opposed to embedded systems). The goal of interactive systems is not primarily to solve problems automatically but to increase user performance (see e.g. the discussion in [Berner et al. 94]). Therefore, we have to accommodate for vague, incomplete and incorrect data - the latter due to difficulties of the user with symptom recognition. In particular with respect to different compromises between knowledge and data acquisition effort and accuracy of the resulting product, the various methods have different advantages and disadvantages. In the following, we discuss general knowledge acquisition strategies with an emphasis on the costs for building and maintaining a knowledge base.

Knowledge bases can be built by knowledge engineers supported by domain experts, by the domain experts themselves or by machine learning techniques. The latter is the least expensive alternative. It usually requires a data base with many cases, where the observations are stored in a standardized form together with the correct solutions. The statistical, case-based and neural classification methods belong to this category. In addition there are inductive learning techniques like the ID3-family of decision tree learning algorithms or the star method for learning rules (for a thorough evaluation see [Michie et al. 94]). However, these algorithms currently cannot solve the knowledge acquisition problem for several reasons. First, a large effort is necessary to produce detailed, standardized documentation forms for data gathering, which is still left to the expert. Second, the raw data is often too low level for learning algorithms, so that experts need to add preprocessing knowledge (which we call data abstraction). Third, it is often quite useful to formalize basic domain knowledge in advance. Fourth and most important, the quality of the generated knowledge is often poor compared to expert knowledge. One common reason is the lack of sufficient cases for generating useful abstractions to classify rare diagnoses. While we do not expect that learning from cases can produce knowledge bases of similar quality as possible with experts, it can be a useful technique to support manual knowledge acquisition.

Since knowledge acquisition with two kinds of highly paid specialists - knowledge engineers and domain experts - is often too expensive, we concentrate on the alternative of domain experts building their knowledge bases largely on their own. The first requirement is a shell with a convenient, easy to learn and fast to use knowledge acquisition interface. Visual programming languages [Burnett & Ambler 94] offer these features and are particularly well suited for diagnostic problem solving, because most knowledge can be represented declaratively. To enter their knowledge the experts have to fill in forms, tables, graphs or hierarchies [Bamberger et al. 97].

2. Experience with building large knowledge bases by experts

In this section, we report experience from three projects, where experts built large knowledge bases in medical, technical and other domains with our diagnostic shell kit D3 [Puppe et al. 96]. Thereby we emphasize the aspects of knowledge restructuring. D3 offers most of the above mentioned methods including categorical, heuristic, statistic, set-covering, functional and case-based diagnostic problem solving methods, and a complete graphical knowledge acquisition interface [Gappa et al 93]. Knowledge in D3 can be used for various purposes:

• consultation, i.e. the user enters case data and the expert system indicates tests for further elaboration and suggests diagnostic and therapeutic options,
• documentation, i.e. the cases are stored in a case base or printed in various forms e.g. as a medical report,
• case-retrieval, i.e. the user searches known cases similar to a new one using case-based reasoning or simple data base queries,
• conventional information look-up based on formal and informal (electronic book) knowledge,
• training, i.e. the user interactively solves a case presented by the computer step-by-step and receives didactic comments generated from the system's knowledge base.

Plant classification

The plant classification system was built by the biologist Roman Ernst [Ernst 96]. It covers the 100 most common flowering plants of the "Mainfranken" region of central Germany. Each plant is characterized by visible features describing flowers, leaves and trunk only, that is, no special instruments are necessary to recognize the features (see Fig. 1). Since they are sometimes ambiguous and difficult to recognize, the method must be able to deal with many low-quality features and be robust enough to tolerate some misrecognized features. The decision tree approach used in many plant classification books does not share these assumptions, because they sometimes rely on features detectable only by special instruments and it usually cannot recover from misrecognized features. Therefore decision trees were discarded.

The most obvious and time-effective approach uses set-covering knowledge stating the features for each plant with typicality (frequency) values. However, our evaluations proved this method to be very sensitive to misrecognized features. To make the system more robust, it was necessary to state not only the typical features, but also to what degree the other features would be untypical for each plant. This knowledge is straightforwardly expressed with heuristic rules, where each feature transfers positive or negative evidence for almost each plant. In the final knowledge base there are more than 10000 one-symptom-one-diagnosis rules, part of them shown in Fig. 2. Since they are entered in D3 through tables like those in Fig. 2 (containing already almost 100 relations), the effort for knowledge editing including fine tuning of the evidence took only about one person month for the expert. Evaluations demonstrated greater robustness than the set covering knowledge base allowing even 1-3 misrecognized features from about 40 without significant deterioration of performance. However, there were still problems with some plants because of their varying phenotypes depending on their environment. Since empirical knowledge was not readily available for the variations, a case-based component was added allowing the system to remember unusual cases (but they must be classified the first time without the system). Therefore, knowledge about a similarity measure was added and the cases already gathered for evaluation of the other methods were used as the basic case set. The results of this evaluation were encouraging taking the restricted case set (150 cases for 100 different plants) available into account, but showed a significant lower performance than the other two methods.

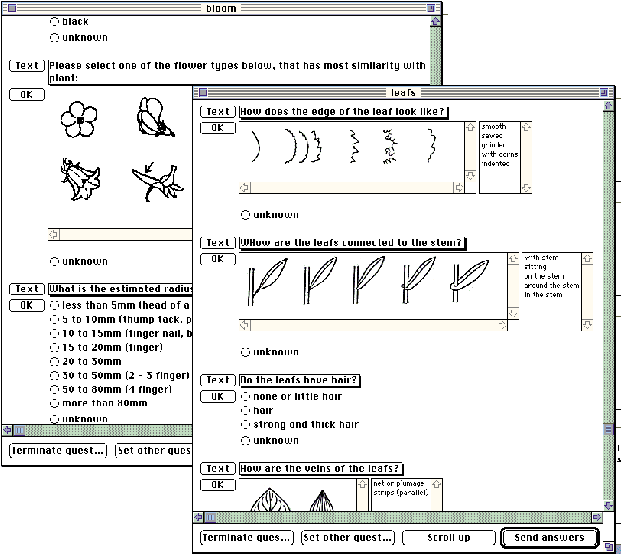
Fig. 1: User questionnaires for entering features of a plant.

Fig. 2. Input of simple heuristic rules with a table. Four plants (column headers) are rated by the features in the lines. In the marked box the following rule is entered: if the "perimeter of the stock" (Stengelumfang) is "round and rather smooth" (rund und eher glatt), there is sometimes (manchmal, p2) evidence for "Taraxacum officinalis" (Wiesen-Löwenzahn).

Another focus of the work was to teach casual users to recognize features correctly with the help of drawings and verbal descriptions. Therefore, a training system was generated from the knowledge base. It contained plant pictures presented to the user, who is supposed to describe their features in terms of the terminology of the system.

The biologist developed the knowledge base without knowledge engineering support using the graphical knowledge acquisition facilities of D3. A large amount of the total development time of six months he spent with gathering, scanning and editing the plants and drawings of typical features.

Service support for printing machines

The goal of this joint project with one of the world's leading manufacturers of printing machines, Koenig&Bauer Albert AG (KBA) in Wuerzburg, is the development of a diagnosis and repair system both for the initial starting-up and subsequent service support of printing machines [Landvogt et al. 97]. Since printing machines are very large and complex, it was clear from the beginning, that one huge knowledge base would be very difficult to maintain. Therefore a concept was elaborated to split the knowledge base in different modules (agents), which can be developed by different experts more or less independently and which are able to cooperate to solve cases (see chapter 7).

It quickly turned out, that a pure knowledge-based system was not sufficient for this purpose, since company technicians expect the computer to hold all relevant information including drawings, parts lists, descriptions, videos and client contacts for the particular machine. A large effort went in expanding the knowledge representation of D3 to link formal and informal knowledge and to integrate viewers for the different information sources.

With respect to continuous maintenance of the knowledge base, it was a major goal of the project, that the KBA workers learnt to develop the knowledge base on their own - ideally spending one day per week for this task, while working the rest of the week on their primary job. The organizational and qualificational aspects of this "self-acquisition" (as opposed to knowledge acquisition with knowledge engineers) are studied by a third project partner IuK ("Institut für sozialwissenschaftliche Technik-Folgenforschung"). From a pure technical point of view, the self-acquisition did work, for KBA experts indeed developed large knowledge bases on their own with the graphical knowledge acquisition interface of D3 (see table 1). However, for quality improvement general modeling principles and technical tricks were discussed with "knowledge consultants".

Problem area	Symptom sets	Symptoms	Diagnoses	Rules
print unit JC	46	365	258	1012
print unit EC	81	691	354	1877
paper run	6	80	103	495
print quality	10	38	69	164
rell changer	54	499	280	1608
rabbet gadget	7	198	101	697
recontrol	44	361	242	980
sum	248	2232	1407	6833

Table 1: Distributed knowledge bases for printing machines: statistics in 1996.

Methodologically, the first approach was based on decision trees, since that seemed most natural to the experts. The underlying strategy is that they quickly generate suspects from the main symptom and have specific questions and tests to find the diagnosis (usually corresponding directly to a repair job). The decision trees are rather broad and flat, with usually only 3 questions in one branch. Accordingly, the key knowledge seemed to lie in the sequence to gather symptoms. This knowledge was available in a compiled form, so that it could be represented directly with dialog-guiding rules. The main problem with this approach arose from the technician's desire for early feedback after having entered the first few symptoms. However, decision trees display results only upon reaching a leaf in the tree. When there are many suspects, often many branches must be explored until discovering the final diagnosis. If the user is too impatient to finish a session, no results at all might be displayed. The main requirement for the system was to display all its suspects all over the time, i.e. initially a large set of ranked hypotheses shrinking subsequently with ruling-out of alternatives. The experts first tried to implement this behavior with heuristic classification, because they preferred the decision tree editor in D3 allowing also easy entering of simple heuristic relations. To convince them to use the better suited set covering classification required to extend that editor to handle those relations as well. The basic knowledge structure is quite simple: For every symptom, all diagnoses covering it are stated. The set-covering problem solver also takes into account confirmation or exclusion of a diagnosis by categorical knowledge. At any time, it displays a list of diagnoses ranked to the degree how well they explain currently known symptoms.

Rheumatology

The primary goals of the expert system RHEUMA from Prof. Schewe (Munich university hospital) are to systematize collecting medical history and clinical data, to assist non-specialist physicians in rheumatic diagnostics, to document patient data, and to automatically generate a patient report. RHEUMA comprises the approximately 70 most common diagnoses in rheumatology. The first approach was based on heuristic classification, because it seemed to be most effective in large medical domains. The results were quite encouraging: In a prospective evaluation with 51 unselected outpatients coming from a second clinic, it stated the final clinical diagnoses (which was used as gold standard) in about 90% of the cases and focused on the correct diagnoses in about 80% % (i.e. in about 90% of the 90% cases with the final diagnoses) [Gappa et al 93]. Since more than 1000 real cases were collected during development and evaluation time, case-based knowledge about a similarity measure was added to RHEUMA to exploit this data. However, due to multiple diagnoses in many cases, the performance of the case-based classification component scored significantly lower than heuristic problem solving.

In a recent extension the program is also used as a training system with reversed roles of computer and user: The training system presents case data step by step and invites the user to recognize symptoms from pictures, order tests and suggest hypotheses. For all these decisions, the training systems computes didactic feed-back by comparing them to its own preference in the given diagnostic context. The training system was evaluated in several mandatory courses for students at Munich medical school with good results [Schewe et al. 96]. While technically no modifications of the diagnostic knowledge base were necessary, the heuristic rules turned out to be too complicated for teaching purposes. To improve its explanatory capabilities, a set-covering (pathophysiologic) model is currently added to the heuristic and the case-based knowledge base.

Both development and maintenance of the knowledge base was achieved by the expert himself. He was even able to model his knowledge according to different paradigms. Similar systems were developed from other medical authors with D3 for large fields like neurology, cardiology (an example of the definition of a rheuma-related differential diagnosis from the cardiology knowledge base is shown in Fig. 3), hepatology, hematology as well as in many smaller domains like thyroid diseases or acute abdominal pain [Puppe et al. 95].

1. Malar rash
2. Discoid rash
3. Photosensitivity
4. Oral ulcers
5. Arthritis
6. Serositis
7. Renal disease	a. > 0.5 g/dl proteinuria, or
	b. >= 3+ dipstick proteinuria, or
	c. Cellular casts
8. Neurologic disease	a. Seizures, or
	b. Psychosis (without other cause)
9. Hematologic disorders	a. Hemolytic anemia, or
	b. Leukopenia (< 4000/µL), or
	c. Lymphopenia (< 1500/µL), or
	d. Thrombocytopenia (< 100.000 µL)
10. Immunologic abnormalities	a. Positive LE cell preparation, or
	b. Antibody to native DNA, or
	c. Antibody to Sm, or
	d. False-positive serologic test for syphilis
11. Positive antinuclear antibody (ANA)

Fig. 3. Definition of "Systemic Lupus Erythematosus" (SLE), which requires that at least 4 of the 11 criteria are met (upper part) and its graphical knowledge acquisition (lower part) in two versions with complex (A) and simple (B) n-of-m rules. The leftmost rule in both versions represent the definition stated in the upper part with a definite ("defi..." in the top most line) conclusion. The other two rules of each part infer an evidence category (probable or possible). The rules in (A) and (B) represent the same content, but in (B), 4 supplementary rules are necessary for inferring the symptom interpretations stated in the last 4 lines (D; renal criterion, neurologic criterion, hematologic criterion and immunologic criterion), which are omitted. Such a rule might be "if hematologic evidence is Thromocytopenia or Lymphopenia or Leukopenia or Hemolytic Anemia, then infer Hematologic Criterion = positive". This rule represents the same knowledge as expressed in the 4 lines about hematological evidence (C) marked with "+O3" within the complex n-of-m rules (A).

3. Flexibility in knowledge acquisition

Successful self-acquisition of knowledge by domain experts in the above mentioned projects was made possible by D3's graphical knowledge acquisition component using graphical aggregation and abstraction techniques for managing the complexity of large knowledge bases [Gappa et al. 93, Bamberger et al. 97]. It not only simplifies the process of knowledge editing, but also makes the represented knowledge more transparent to the experts. But equally important is that the experts feel comfortable with the problem solving method used. Since there is often little time to train them, the starting point must be their experience with solving problems, i.e. there must be a match between the problem solving method of the computer and their own. Therefore a large variety of problem solving methods should be offered to them so they can pick up and configure the most suited. In the examples and in many other projects, switching or upgrading between different methods is necessary. While some methods are better suited for solving not so difficult problems, others require more initial modeling efforts but offer a higher degree of sophistication. Since the complexity of the problem is often not evident at the beginning, one wants to start with easy models and refine them if necessary. Therefore, from a representational point of view the knowledge for the different problem solving methods should be reused as much as possible to allow the domain experts to switch between methods with minimal effort. Some typical pathways through the problem solving methods are:

• Start with set covering knowledge and add heuristic knowledge for higher diagnostic precision and a case-based component for dealing with untypical cases (plant recognition project).
• Start with decision trees and "upgrade" to set-covering or heuristic knowledge for dealing with uncertainties or incompleteness (printing machine project). To exploit cases gathered over time add case-based and/or statistical knowledge.
• Start with heuristic knowledge and add set-covering knowledge for better explanations (rheumatology project). To exploit cases gathered over time add case-based and/or statistical knowledge.
• Start with a coarse functional model and add decision trees for checking suspected components (experiment in the rabbet gadget of printing machines; compare table 1).

If switching to another problem solving method implied building a completely new knowledge base, the costs would be in general prohibitively high. However, there is much potential for reuse:

• Terminology and informal knowledge: The basic terminology of symptoms or observations (input) and diagnoses (output) should remain the same within all methods. This includes all informal knowledge linked to the terminology like annotations, pictures, drawings etc., which often comprises a great deal of the work invested (e.g. plant recognition, diagnosis of printing machines, and rheumatology projects). In addition, constraints on input values (e.g. that the systolic blood pressure must be higher than the diastolic blood pressure) are method-independent and can be connected to the terminology.
• Data abstraction knowledge: The raw symptoms often are too ambiguous for direct interpretation. Therefore, they should be preprocessed to symptom abstractions. In our medical knowledge bases like e.g. RHEUMA, data abstractions comprise a large part of the total knowledge. Since this is rather independent from the problem solving method, once formalized, it can be reused by any other method.
• Data gathering knowledge: Knowledge on how to gather data comes in two forms: hypothetico-deductive (if a hypothesis is suspected, tests useful for its clarification should be done taking their costs/benefits ratio into account, e.g. rheumatology project) and compiled like in decision trees or other categorical rules (if certain states, e.g. observations or intermediate results, are detected, then certain data gathering procedures should be done routinely; e.g. printing machine project).
• Categorical knowledge for diagnostic reasoning: Knowledge for confirming or excluding diagnoses is useful for all methods and should be considered first (e.g. printing machine project). Therefore, categorical knowledge should be represented in a way compatible with all methods.
• Diagnostic profiles: Most diagnostic methods have an explicit representation of the features relevant for a diagnosis, while the form and the additional knowledge included may vary. Therefore, it may be useful to represent the profile of a diagnosis independently from its particular use inside a method (rheumatology project).
• Abnormalities of observations: Different observations have different diagnostic importance. In particular, normal features (like e.g. heart rate = 60) are much less important than abnormal ones (e.g. heart rate = 105). In addition the importance of abnormal symptoms may vary (e.g. low or extreme pain intensity). While in some domains, this knowledge is rather static, in other domains it might depend on a few general parameters (e.g. normal ranges of lab-parameters often depend on gender and age). Sometimes however, it depends on the whole system model (e.g. whether a bit in a circuit is 0 or 1) and therefore cannot be represented in a special module.

Taking into account this rather large potential of knowledge reuse, we designed a combined inference structure for the different diagnostic problem solving methods to exploit this potential. Besides allowing a soft transition among methods, it also encourages building knowledge bases with several methods in parallel to combine their advantages.

4. Knowledge sharing among diagnostic problem solving methods

The obvious solution for knowledge reuse is to modularize problem solving methods according to reusable knowledge types. Hence we introduced separate modules for data gathering, data abstraction, categorical valuation of diagnoses and non-categorical valuation of diagnoses. It is only the latter that differs among different methods. Furthermore, it is desirable that all models share the terminology. In addition, the diagnostic profile, i.e. a list of relevant features for a diagnosis, and the abnormality of observations are represented as separate data structures supporting knowledge representations of different methods. In the following, we focus on how different diagnostic might share and reuse that knowledge.

A standardized representation of observations and solutions might already seem sufficient for case based classification methods (in addition to cases). Additional useful knowledge includes the similarity measure, the general information about abnormalities and data abstractions. Diagnostic profiles might also be useful for adding diagnosis-specific adaptations of the contribution of certain observations to the overall similarity between cases. Categorical valuations of diagnoses should take preference over any similarities between cases. Otherwise, that knowledge would have to be coded within the similarity measure, e.g. to prevent a case of a male patient to be compared to a case of pregnancy. Since case-based reasoning is not very well suited to support data gathering (in particular when mostly unspecific symptoms are known so far), it greatly gains by using compiled data gathering knowledge.

Heuristic and set-covering knowledge can exploit nearly all reuse facilities listed above: terminology, data abstraction, compiled and hypothetico-deductive data gathering knowledge, categorical knowledge for diagnostic reasoning, and diagnostic profiles. For example, after implementation of this knowledge for heuristic classification, only the particular formalization of the heuristic rules based on the diagnostic profiles has to be reformulated by set-covering relations (and vice versa). In addition, set-covering classification needs knowledge about abnormalities of observations.

In troubleshooting domains, set covering knowledge can often be viewed as a compiled form of functional models:

- Discrepancies (functional) correspond to abnormal observations (set covering),

- abnormal component states (functional) correspond to primary diagnostic causes (set covering),

- abnormal parameters of materials (functional) correspond to intermediate states (set covering).

To maximize knowledge reuse, we conceptualized and implemented the functional model based on these correspondings as an extension of the set-covering module [Kohlert 96].

Statistical classification mainly uses knowledge about a priori probabilities and conditional probabilities of effects given the causes. Both are computed from large case sets. They can reuse knowledge about terminology, data abstraction, data gathering and categorical knowledge for diagnostic reasoning. Given this knowledge, only a subset of independent symptoms and mutually exclusive diagnoses must be added for the straightforward application of the Theorem of Bayes. Bayesian nets require in addition the specification of the net topology, which is based on the same principles as in set covering classification and therefore can be reused from the diagnostic profiles.

For categorical classification, no special knowledge besides the shared knowledge parts is necessary: Decision trees and decision tables (by definition) contain only categorical knowledge for diagnostic reasoning, and decision trees in addition use compiled data gathering knowledge.

Fig. 4 summarizes an integrated inference structure for diagnostic problem solving combining problem solving methods for categorical, heuristic, statistic, set-covering, functional and case-based classification optimized for knowledge reuse. Knowledge not specific for a certain problem solving method is separated out as independent modules (1.1 - 1.4 in fig. 4) being (re)used by any problem solving method. Therefore, the specific part of a problem solving method can be reduced to its "non-categorical valuation of diagnoses" (1.5 in fig. 4). But even among these modules some reuse of knowledge is possible as mentioned above (diagnostic profiles, abnormality of observations), but not expressed in the inference structure. A detailed description of the tasks and methods is given in the appendix.

Fig. 4. Combined inference structure for categorical, heuristic, statistic, set-covering, functional and case-based classification in an and/or graph. Or-nodes, from which one or more successors can be selected, represent methods and are printed in ovals and italics. And-nodes denote tasks. The appendix presents details for the modules including informal description, input, output and necessary knowledge.

5. Comparison with other inference structures

Our modularization of diagnostic problem solving methods is distinguished from others in its breadth of methods and in its emphasis of knowledge reuse among the methods. In the following we compare it in some detail with the inference structure presented in [Benjamins 95], because this is based on a rather broad survey on the literature of diagnostic systems. The three main tasks are symptom detection, generation of hypotheses for the symptoms detected and finally discrimination of the hypotheses. Symptom detection can be viewed as a classification task in itself or may be done by the user or by comparing expected with observed values. Expected values can be looked up in a data base or predicted by a simulation. For the comparison task, many methods exists ranging from an exact comparison (if expected and observed value are identical, the symptom is considered normal, otherwise abnormal) to various abstractions. For the hypothesis generation task Benjamins offers only two methods: compiled and model-based. Compiled methods consists of the three tasks symptom abstraction, association of (abstracted) symptoms with diagnoses and a probability filter. Model-based methods consists of three methods too: Find possible causes (contributors) for each abnormal symptom, combine the contributors to sets of hypotheses being able to explain all abnormal symptoms and filter out inconsistent hypotheses by simulating their effects in the model. If there are several hypotheses left, additional observations are gathered in order to discriminate between the hypotheses. A summary of the inference structure is shown in fig. 5.

In contrast to the six problem solving methods in Fig. 4, Fig 5 contains only two: compiled and model-based, with many variants. The correspondences of the main steps are:

• Hypothesis generation (2.2) and Non-Categorical valuation (1.5)
• Hypothesis discrimination (2.3) and costs/benefits analysis (1.1.3)

The main differences concern the emphasis of categorical knowledge. While nearly lacking in the inference structure of [Benajmins 95], in our modularization it comes in many forms: standardized test indication, plausibility check of answers, inferences of follow-up questions, data abstraction, categorical valuation of diagnoses, filter for symptoms and detection of abnormal symptoms. If categorical knowledge exist, it should be applied with priority, even for model-based problem solvers. This holds in particular, if one cannot guarantee the completeness of the knowledge base and therefore cannot apply the closed world assumption (e.g. reasoning by elimination).

Another main difference is in the symptom detection task. Our modularization lacks a step to generate expectations by prediction (2.1.1.1.2), but instead offers the general mechanism of data abstraction (1.3) and the detection of abnormal symptoms (1.5.5.1). The latter is roughly equivalent to the look-up and compare step (2.1.1.1.1 and 2.1.1.2). The data abstraction step is available in [Benjamins 95] in the compiled hypothesis generation method only. However, its mechanisms including arithmetic, aggregation and abstraction are often powerful enough to detect abnormal symptoms (e.g. inferring whether a measurement value like energy consumption in a technical device is too high or computing the shock-index from heart beat frequency and blood pressure). One might argue, that a prediction model is needed anyway for model based diagnosis in the hypothesis generation step, and therefore the respective knowledge acquisition effort cannot be avoided. However, we found that generating symptom expectations often requires a more detailed model than generating and filtering hypotheses. Typical applications, where it is not necessary to predict symptom expectations, comprise not only medical diagnosis, but also technical diagnosis, if one can built upon high level observations from e.g. automatically generated error messages or humans. Of course, this does not hold in all technical domains like e.g. circuit diagnosis, where prediction is necessary for detection of abnormal symptoms. It should be noted, that e.g. statistical and case-based classification are difficult to apply in such domains.

Fig. 5. Condensed inference structure for diagnosis from [Benjamins 95] compared with table 2 (in parentheses). "..." indicates further refinements in [Benjamins 95].

A minor difference is the kind of modularization of the model based hypothesis generation method in both approaches. The three steps in "find contributors, transform to hypothesis set and prediction based filtered" (2.2.2.1 - 3) in [Benjamins 95] are distributed over the two steps "best cover based on single and multiple diagnoses" (1.5.4.3 - 4 and 1.5.5.3 - 4). The reason for our distinction is, that it is quite efficient to compute the cover for each relevant single hypothesis taking into account both covering and prediction, and the best single hypotheses can use the generalized knowledge for selecting the next test with the best costs/benefits ratio (1.1.3). The computational expensive step of computing multiple diagnoses for the best complete cover is often best done based on the results of the single cover step at the end or on explicit demand of the user.

6. Discussion

Different diagnostic methods offer different theoretical and practical advantages: they use different knowledge (categorical, empirical, case-based or causal) and they have different tradeoffs (e.g. knowledge acquisition time versus diagnostic accuracy, effort for building the initial prototype versus continuous maintenance) and explanation capabilities. Therefore, a major design goal for the diagnostic shell kit D3 - besides offering the most important methods - was to allow reuse of as much knowledge as possible when switching from one method to another. D3`s modularized inference structure is optimized towards this goal. All methods reuse knowledge about terminology and taxonomy of symptoms and diagnoses, local and global data gathering strategies (test selection and follow-up questions), plausibility checks, data abstraction and categorical valuation of diagnoses. Other knowledge structures shared by some methods are symptomatic profiles for diagnoses as well as knowledge about the importance and abnormality of symptom values. The knowledge representations and their visualization by graphical knowledge editors encouraged domain experts to represent their knowledge according to different paradigms. While this is useful for finding out the best method for both the domain and the mental model of the domain expert, it is even more useful for combining the advantages of different models. In medium or large medical domains such as rheumatology or cardiology this might be:

• high diagnostic accuracy using categorical and heuristic knowledge with complex n-from-m rules,
• best explanation capability by using set-covering (pathophysiologic) knowledge, and
• a kind of automatic learning mechanism based on the gathered cases by case-based classification.

A further step in knowledge reuse is to take more advantage of different problem solvers about the same domain, e.g. a heuristic, set-covering and case-based reasoner. If they propose different solutions for the same case, coming up with a combined solution requires meta-knowledge about the general quality of the knowledge bases and about the assessments of the individual solutions. Cooperation can also take place during the problem solving process, e.g. using heuristic or case-based knowledge for fast hypothesis generation being tested by e.g. a simulation in a functional model.

A more ambitious step is the cooperation of independently developed knowledge bases like e.g. for different medical domains or different aggregates of large technical systems such as printing machines [Bamberger 97]. This distributed problem solving approach requires knowledge about:

• team formation with agents having different, but maybe overlapping knowledge,
• about self-competence and competence of other agents in order to decide, when and what other agent to consult,
• about translation of facts and results for communication with other agents, and
• knowledge for comparing and integrating different solutions.

Distributed problem solving is an important step to reduce the size and thereby the complexity of knowledge bases and to increase reuse, because for example a knowledge base for X-ray interpretation can be consulted by many different medical knowledge bases.

7. References

Bamberger, S. (1997). Cooperating Diagnostic Expert Systems to Solve Complex Diagnosis Tasks, in Proc. KI-97, Brewka, G., Habel, C. and Nebel, B.: Advances in Artificial Intelligence 1997, LNAI 1303, Springer, 325-336.

Bamberger, S., Gappa, U., Kluegl, F. and Puppe, F. (1997). Komplexitätsreduktion durch grafische Wissensabstraktionen [Complexity reduction by graphical knowledge abstractions], in Mertens, P. and Voss, H. (eds.): Proc. of XPS-97, 61-78, infix.

Benjamins, R. (1995). Problem-Solving Methods for Diagnosis and their Role in Knowledge Acquisition, International Journal of Expert Systems: Research and Application.

Berner, E. et al. (1994). Performance of four Computer Based Diagnostic Systems, New England Journal of Medicine 333, 1792-1796.

Breuker, J and van de Velde, W. (eds. 1994). COMMONKADS Library for Expertise Modeling - Reusable Problem Solving Components, IOS-Press.

Burnett, M and Ambler, A. (1994). Declarative Visual Programming Languages, Journal of Visual Languages and Computing 5, Guest Editorial, 1-3.

Ernst, R. (1996). Untersuchung verschiedener Problemlösungsmethoden in einem Experten- und Tutorsystem zur makroskopischen Bestimmung krautiger Blütenpflanzen [Analysis of various problem solving methods with an expert and tutoring system for the macroscopic classification of flowers], Master thesis, Wuerzburg university, Biology department.

Fensel, D. and Benjamins, R. (1997). Assumptions in Model-Based Diagnosis, AIFB-Internal Report 360, Karlsruhe University.

Gappa, U., Puppe, F., and Schewe, S. (1993). Graphical Knowledge Acquisition for Medical Diagnostic Expert Systems, Artificial Intelligence in Medicine 5, 185-211.

Gappa, U. and Puppe, F. (1998). A Study of Knowledge Acquisition - Experiences from the Sisyphus III experiment of rock classification, To appear in Proc. of 12th Banff Knowledge Acquisition for Knowledge-Based Systems Workshop (KAW-98).

Kohlert, S. (1995). Eine Shell für minimale funktionale Klassifikation am Beispiel der Druckmaschinendiagnostik [a shell for minimal functional classification exemplified on printing machine diagnosis], Master Thesis, Wuerzburg University, Informatics department.

Landvogt, S., Bamberger, S., Hupp, J., Kestler, S. and Hessler, S. (1997). KBA-D3: ein Experten- und Informationssystem zur Fehlerdiagnose von Druckmaschinen, [KBA-D3: an expert and information system for troubleshooting in printing machines] in Mertens, P. and Voss, H. (eds.): Proc. of XPS-97, 167-170, infix.

Michie, D., Spiegelhalter, D., and Taylor, C. (eds., 1994). Machine Learning, Neural and Statistical Classification, Ellis Horwood.

Puppe, B., Ohmann, C., Goos, K., Puppe, F. and Mootz, O. (1995). Evaluating Four Diagnostic Methods with Acute Abdominal Pain Cases, Methods of Information in Medicine 34, 361-368,

Puppe, F. (1993). Systematic Introduction to Expert Systems - Knowledge Representations and Problem Solving Methods, Springer.

Puppe, F., Gappa, U., Poeck, K. und Bamberger, S. (1996). Wissensbasierte Diagnose- und Informationssysteme [Knowledge based diagnosis and information systems], Springer.

Schewe, S., Quack, T., Reinhardt, B., and Puppe, F.(1996). Evaluation of a Knowledge-Based Tutorial Program in Rheumatology - a Part of a Mandatory Course in Internal Medicine, in: Proc. of Intelligent Tutoring Systems (ITS-96), Springer, 531-539.

Van Harmelen, F. and ten Teije, A.(1998). Characterizing Problem Solving Methods by Gradual Requirements: Overcoming the yes/no Distinction, in Proc. KEML-98, 8^th Workshop on Knowledge Engineering: Methods & Languages, 1-15, Univ. Karlsruhe, 1998. (URL: http://www.aifb.uni-karlsruhe.de/WBS/dfe/keml98).

Appendix: Description of Tasks and Methods for Fig. 4

1. Classification (Diagnosis)

Description: Selection of one or more diagnoses based on symptoms which may be given or which must be requested.

Input: Observed Symptoms.

Output: Diagnoses.

Knowledge: s. subtasks (1.1 - 1.5).

1.1 Test selection

Description: Selection of tests, which should be performed for clarification of the case.

Input: Currently known symptoms and suspected and confirmed diagnoses.

Output: Tests (question sets).

Knowledge: s. subtasks (1.1.2 + 1.1.3).

1.1.2 Standardized indication

Description: Selection of tests based on standardized procedures.

Input: Facts.

Output: Tests.

Knowledge: 1. Rules for indication of tests from constellation of facts.

2. Rules for contraindication of tests from constellation of facts.

3. Cost categories for tests. If more than on tests is indicated, the test with the lowest cost category will be selected.

1.1.3 Costs/benefits analysis

Description: Selection of tests for best clarification of suspected diagnoses with the lowest costs.

Input: Suspected diagnoses (+ facts)

Output: Test

Knowledge: It is specified, which diagnoses how well will be clarified by a test. In addition the static (represented by an attribute) and dynamic (represented by rules) costs of a tests are stated.

1.2 Data gathering

Description: Data gathering from the user or from external data sources.

Input: Test (question set).

Output: Assignment of values to the questions of the test.

Knowledge: s. subtasks (1.2.1 - 1.2.3).

1.2.1 Interviewer component

Description: User interface for entering data or program interface for external data sources, which is not treated in this paper.

1.2.2 Plausibility check of answers

Description: Plausibility check of input data.

Input: Answers to questions

Output: o.k. or error message.

Knowledge: 1. valid value ranges for each question

2. Constraints for recognition of inconsistencies between different answers.

1.2.3 Inference of follow-up questions

Description: Determination, whether follow-up questions should be asked.

Input: Answers to questions

Output: New questions

Knowledge: Rules for inferring questions.

1.3 Data abstraction

Description: Derivation of symptom abstractions. They include arithmetic formulas for combining quantitative data, the abstraction of quantitative to qualitative data, and the aggregation of qualitative data.

Input: Symptoms

Output: values for symptom abstractions.

Knowledge: 1. Terms for symptom abstractions and their ranges.

2. Rules for inferring the symptom abstractions, whose action part may be a number, a formula or a qualitative value.

3. Schemes for transformation of numerical to qualitative values.

1.4 Categorical valuation of diagnoses

Description: Confirmation or exclusion of diagnoses with categorical rules.

Input: Facts

Output: Confirmed or excluded diagnoses.

Knowledge: Rules, whose action part establish or exclude a diagnosis .

1.5 Non-categorical valuation of diagnoses

Description: Valuation of diagnoses based on symptoms with vague knowledge.

Input: Facts

Output: Suspected and/or confirmed diagnoses.

Knowledge: Depends on problem solving methods (s. 1.5.1 - 1.5.5)

1.5.1 Heuristic valuation

Description: Diagnoses are confirmed, if their accumulated evidence surpasses a threshold or if they are better than their competitors (differential diagnoses).

Input: Facts

Output: Suspected and/or confirmed diagnoses.

Knowledge: 1. Rules, whose action part contains a diagnoses and a positive or negative evidence category.

2. A-priori frequency: Category from extremely rare via average to extremely common.

3. Rules for dynamic correction of the a-priori frequency based on facts.

4. Knowledge about direct competitors belonging to a diagnostic class, i.e. if the diagnostic class is confirmed, the highest rated competitor inside the class should be confirmed.

1.5.1.1 Inference of suspected diagnoses

Description: A diagnosis is suspected, if its accumulated evidence is higher than a threshold and lower than another threshold. Suspected diagnoses are used as input for the cost benefits analysis.

1.5.1.2 Inference of confirmed diagnoses

Description: A diagnosis is confirmed, if its accumulated evidence is more than the second threshold for suspected diagnoses or if it is the leader of a competitor class. Confirmed diagnoses can be treated in rule preconditions like symptoms.

1.5.2 Simple statistic valuation

Description: Determination of the best diagnosis from a complete and exclusive set of alternatives with the Theorem of Bayes.

Input: Symptoms (which should be independent of each other).

Output: Diagnosis.

Knowledge: A-priori probability of diagnoses P (D) and conditional probabilities P (D/S) for all singular symptom/diagnosis combination, which should be extracted from large representative case sets.

1.5.3 Case based valuation

Description: For a new case without solution one or more most similar cases from case set are extracted. If the similarity is high enough, the diagnoses from the old case(s) are transferred to the new case. The similarity of two cases is computed from the similarity of corresponding symptoms.

Input: Symptoms and (optional) a view, i.e. an abstraction layer.

Output: Most similar case(s) and their diagnoses.

Knowledge: For each symptom: Abstraction layer, weight, abnormality of its values, similarity type, similarity information. For each diagnosis it is possible, to state a specific weight and similarity information per symptom overriding the defaults.

1.5.3.1 Filter for symptoms

Description: Some symptoms are filtered out, which should not be used for computation of similarity.

Input: Symptoms and view (abstraction layer).

Output: Subset of symptoms.

Knowledge: Abstraction layer of symptoms, which is compared with the input abstraction layer.

1.5.3.2 Preselection of cases

Description: All cases are preselected, which are at least in one important symptom similar to the new case.

Input: Symptoms

Output: Cases

Knowledge: Important symptoms are determined by their weight and their abnormality.

1.5.3.3 Elimination of cases with impossible diagnoses

Description: From the preselected cases those are sorted out, which have diagnoses being incompatible with the symptoms of the new case based on the categorical valuation.

Input: Cases, excluded diagnoses.

Output: Subset of cases.

Knowledge: Categorical valuation (1.4).

1.5.3.4 Complete comparison of cases

Description: Determination of similarity between two cases as percentage number.

Input: New case and n old cases for comparison.

Output: For each old case the percentage of similarity.

Knowledge: s. 1.5.3.

1.5.3.5 Determination of diagnoses

Description: From a list of similar cases, the solution for the new case is determined. There are several options: Take over of the diagnoses from the most similar case, if distance is high enough; majority vote of several very similar cases, if some of them have the same diagnoses; or more complicated transfers.

Input: Ordered list of cases with similarity rating.

Output: Diagnoses.

Knowledge: Diagnoses of the old cases and similarity ratings.

1.5.4 Set covering valuation

Description: Selected is the diagnosis or set of diagnoses, which can cover (predict, explain) as much as possible of the facts and predict as less as possible unobserved facts taking into account the general frequency of the diagnoses. Completeness of the covering relations is not assumed.

Input: Symptoms (and optional abstraction layer).

Output: Diagnosis or set of diagnoses.

Knowledge: 1. Rules, whose precondition are a diagnosis and whose action are facts being covered by that diagnosis. The rules may have assumptions and frequency information.

2. Abstraction layer, weight and abnormality of symptoms.

3. A-priori frequency: Category from extremely rare via average to extremely common.

4. Rules for dynamic correction of the a-priori frequency based on facts.

5. Weight and abnormality information for symptoms.

1.5.4.1 Detection of abnormal symptoms

Description: Symptoms are rated according their abnormality.

Input: Symptoms.

Output: Abnormality rating of symptoms.

Knowledge: Knowledge about the abnormality of the symptom values.

1.5.4.2 Elimination of impossible diagnoses

Description: All diagnoses excluded by categorical reasoning are eliminated.

Input: Diagnoses.

Output: Subset of diagnoses.

Knowledge: Knowledge of categorical valuation (1.4).

1.5.4.3 Best cover based on single diagnoses

Description: Each diagnosis checks its rating how well is covers the symptoms. The diagnosis are sorted and the best diagnoses are treated like suspected diagnoses for test selection (s. 1.1.3).

Input: Symptoms.

Output: Ordered list of diagnoses.

Knowledge: s. 1.5.4.

1.5.4.4 Best cover based on multiple diagnoses

Description: Computation of a set of diagnoses, which together explain the symptoms better than a single diagnosis and which are according to their combined frequencies not too improbable.

Input: Symptoms and list of single diagnoses with their covering relations.

Output: Multiple diagnoses.

Knowledge: Frequency and covering relations of single diagnoses.

1.5.5 Functional valuation

Description: Diagnoses are viewed as states of components and symptoms correspond to materials or signals between the components. The goal is to find those component states, which can predict (explain, cover) the normal and abnormal measurements of materials or signals.

Input: Measurement of materials and signals.

Output: Faulty component states.

Knowledge: Model of the normal behavior of a (technical) system, how input materials are transformed by components to output materials. The components have a normal state and various faulty states (diagnoses), whose behavior is described by rules, inferring values for the output materials from the input materials. The materials consist of parameters, which are represented as symptoms, if they can be measured, or by diagnoses, if they are used for further inferences. With these assumptions and transformations, the functional valuation can be viewed as an extension of the set covering valuation.