For those readers who care
about layout and properly formatted papers, a PostScript
version is available.
For those readers who care
about layout and properly formatted papers, a PostScript
version is available.
Supported
by a TMR project financed by the European Commission. Project: ERBFMBICT961130.Secondly, we show that characterisations of problem-solving methods should be stated in gradual terms, and not in terms of yes/no requirements. Such a gradual approach to characterising problem-solving methods allows methods to use domain knowledge that only partially fulfills the requirements, in which case the methods still produce useful, although suboptimal solutions. Problem-solving methods with such gradual behaviour can be applied and re-used in a wider set of circumstances than classically characterised methods.
Together with ontologies they are now the central notion around which the questions of Knowledge Engineering are discussed: construction of knowledge-based systems, and re-use of both knowledge contents and knowledge structure. Problem solving methods describe in a domain-independent way efficient reasoning strategies for specific problem classes. They require specific types of domain knowledge and introduce specific restrictions on the tasks that can be solved by them [Fensel & Straatman, 1996] [Fensel et al., 1997].
Because of the central role that PSMs play in current Knowledge Engineering research, characterising their properties is of major importance. Such properties of PSMs are required for many of the potential uses that can be made of PSMs: configuration of PSMs, either by hand or automatically [tenTeije et al., 1998]; [Stroulia & Goel, 1997] selection of PSMs from a library, also known as indexing [Benjamins, 1994,Motta & Zdrahal, 1998]; and verification and validation of PSMs [vanHarmelen & tenTeije, 1997,Cornelissen et al., 1997,Marcos et al., 1997]
This paper is concerned exactly with how to characterise PSMs. In the next section (§ 2), we will review and extend the most prominent existing approach to characterising PSMs. This review will expose an implicit assumption in this work, which we will call the yes/no-distinction on requirements. In section 3, we claim that this distinction unnecessarily restricts the characterisations of PSMs. In subsequent sections we will use a simple classification problem as an example to illustrate how the yes/no-distinction can be overcome by giving gradual characterisations of properties of a number of simple PSMs for this classification problem. For instance, we show that our gradual approach allows us to use the hierarchical classification method, which was intended for hierarchical knowledge represented in a perfectly balance tree, also in cases where the hierarchical knowledge can be only represented in a less balanced tree. In practice, we will often find this kind of hierarchical knowledge. Such gradual characterisations of PSMs can be exploited in the configuration, selection and verification of problem solving methods.
BFS96 first define the ``ideal relation'' between the goal-statement and the functionality achieved by a PSM. Secondly, they formulate how domain- and goal-related requirements can be used to bridge the gap between the ideal goal-statement and the actual functionality of a PSM. Thirdly, they describe how domain-related requirements can be exchanged for goal-related requirements (and vice versa).
We will follow the general line of their work, with the following differences: (i) we have a much stronger ``ideal relation'' between the goal-statement and the PSMs functionality; (ii) this results in an additional type of goal-related requirement. Without this additional type of requirement, many natural problem-solving methods cannot be properly characterised; (iii) we show that the exchange of requirements can be performed in a gradual way, allowing for a much finer-grained characterisation of PSMs.
.
.
.
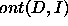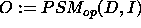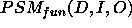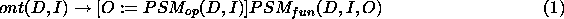
A final concept is the goal relation that must be achieved with the
PSM: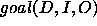 
. The ideal situation
would be that the functionality exactly coincides with the goal:
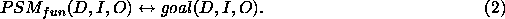
is required (ie. the 
direction).
Instead, we require both soundness and completeness of the PSM with respect
to the ideal goal (in formula (2)
above).
,
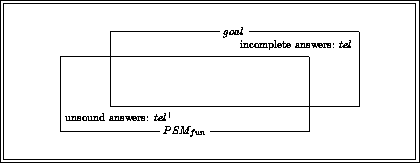
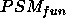goal, 
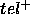and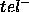 
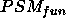is sometimes ``larger'' than the goal (the PSM gives some unsound answers, 
)
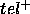and sometimes ``smaller'' (the PSM misses out on others,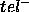 
).
To characterise the relation between goal and functionality, we give names
to the areas where they differ:
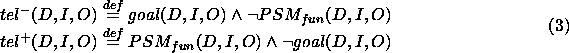
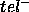represents the incomplete
answers: tuples in goal but not in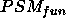 
,
while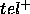 
represents the unsound
answers: the tuples in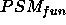 
but not in goal. Notice that this definition directly implies that 
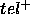and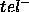 
are disjoint: 
.
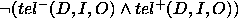Instead of the ideal (2), the
actual relation between goal and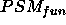 
must now be adjusted, and becomes:
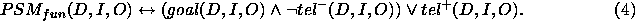
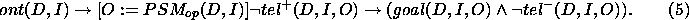
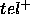), then we
have computed something in the intersection of goal and functionality (since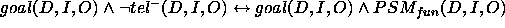 
).
Both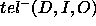 
and 
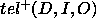characterise the errors that the PSM will make when calculating 
: 
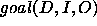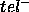characterises the tuples inside goal that we will not compute, and 
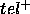characterises the tuples outside goal that we will spuriously compute.
Therefore, both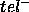 
and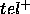 
represent concessions that we have to make to the ideal goal-relation when
using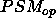 
to compute it. As
a result, both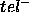 
and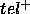 
are called ``teleological'' (= goal related) requirements we place on the
use of our PSM: the PSM is only an acceptable way of efficiently calculating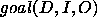 
if we are willing to accept the errors it makes, as characterised by 
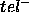and 
.
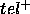Our formula (5) differs from
its counterpart (formula (6) in BFS96). Because of the disjointness of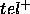 
and 
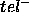, our formula (4)
is equivalent to
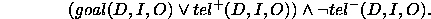
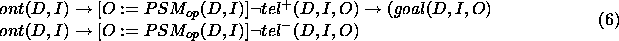
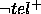corresponds to their
teleological assumptions. This accounts for I/O-tuples which are
computed by the PSM, but which do not satisfy the goal: any computed I/O-tuples
outside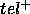 
will satisfy the
goal. It therefore deals with the unsoundness of the PSM. The difference
with our approach lies in the second formula. This accounts for the part
of the goal which is never computed by the PSM: no output of the PSM satisfies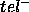 
,
and since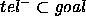 
, these are parts
of the goal that are never computed by the PSM. This characterises the
incompleteness of the PSM.
Notice that our formula cannot be reduced by logical manipulations to the implication in BFS96, showing that it is a semantically different characterisation of the teleological requirements, and not simply notational difference. In later sections we will see simple examples where allowing for incompleteness is required to fill the gap between the goal and a PSM, which cannot be captured in the formula from BFS96.
,
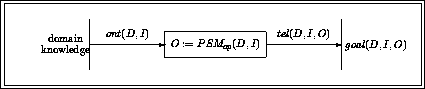
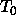their refinement theory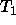 
and their operational theory 
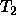correspond to 
, 
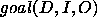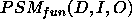and 
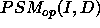respectively.
The work of [Stroulia & Goel, 1997], although less formal then BFS96, is concerned with selecting and configuring PSMs, through matching a PSM's goal with requirements.
[Benjamins & Pierret-Goldbreich, 1997] identifies similar type of requirements of PSMs as discussed in BFS96, and provides a formalisation for a number of such requirements.
While most work on PSMs aim at a domain-independent description of PSMs [Beys & vanSomeren, 1997] also tries to give task-independent characterisations of PSMs.
The work in [Cornelissen et al., 1997] is based on components of PSMs. A hierarchical compositional structure allows the derivation of requirements of the entire PSM on the basis of the requirements on the components.
Despite the variations among all these approaches, they share a common view on PSMs as characterisable by requirements. In the following section we will point out a common implicit assumption (which we will call the ``yes/no distinction'') in all these approaches for which we propose an alternative.
We want to stress that this implicit assumption on the yes/no-nature of requirements in the existing literature is not simply an artifact of the use of classical two-valued logic in the formalisation. We claim that no conceptual notion of a gradually applicable requirements has been studied until now.
In the remaining sections, we will illustrate that it is not at all necessary to assume a yes/no-nature of requirements. We will show how a number of natural requirements on classification methods can be formulated in a gradual way, allowing both the gradual application and the gradual exchange of requirements. Furthermore, we will show how the degree to which a requirement is applicable can be made precise. This will allow us to present precise formula to characterise ``how much'' of a requirement is applicable. This precise ``degree of applicability'' can then be used to apply the ontological version of the requirement as much as possible (thereby strengthening the PSMs functionality as much as possible), while moving the ``remaining'' inapplicable portion of the requirement to the teleological category, (thereby weakening the required goal as little as necessary).
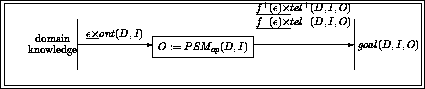
Our proposed extension of the existing framework is paraphrased graphically
in figure 3, where 
symbolises the degree to which an ontological requirement is applicable,
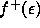and 
and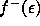 
the degrees to which the corresponding teleological requirement must still
be applied. The functions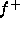 
and 
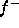symbolise the precise
relation that can be formulated on how much of a teleological requirement
can be relaxed when an ontological requirement is strengthened (or vice
versa).
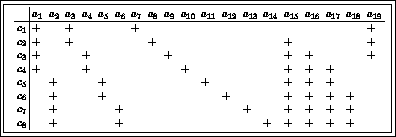
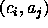in the table indicates that any member of the class 
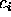has value ``yes'' for the attribute 
.
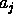We allow attributes to be unknown. Such an unknown value for an attribute
does not rule out the corresponding class.
We limit our examples to binary attributes (using values ``yes'' and ``no''), but all our results also hold for domains with attributes that range over more than two possible values (e.g attribute color has value red, white or blue).
We will formalise classes as con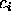stants 
,
and attributes as constants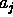 
.
A + is figure 4 is formalised
as the formula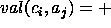 
. In other
words, the domain knowledge is the conjunction of all of these equalities: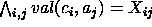 
.
When the table entry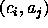 
is
empty, no equality is present. Observations will be formalised as equalities: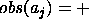 
means that 
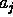has been observed
as present;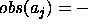 
means that 
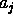has been observed as absent (ie, input data are a conjunction of such equalities).
If no observation has been done for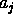 
,
or when an observation returned ``unknown'', then the equality is not present
in the input.
The classification of an individual as belonging to class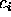 
is formalised by the predicate 
.
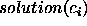Formalisation of assigning the individual to a class by the predicate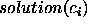 
.
We limit ourselves to single-class solutions, where an individual is assigned
to at most one class. (Composite solutions would be written as a conjunction
of 
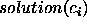). Notice that it is
still possible to have multiple single-class solutions as competing alternative
solutions (written as a disjunction of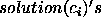 
).
We will deal with two variations of classification:
This definition demands that all required attributes must have
been observed. This means that the value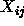 
for attribute 
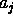is required
for the class 
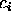. If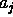 
is known but has the wrong value, or 
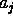is unknown, then 
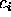is not
a solution.
This requires only that all observed attributes have the right
value, which means that an unknown value for an attribute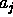 
is allowed, while 
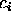is still
a possible solution.
Notice that (2) is weaker than (1) because (2) limits its demands to known attribute-values.
We assume two kinds of table-entries: those table-entries that are necessary for a class, and those that are possible for a class. We will call these POS and NEC attributes respectively. These two types of table-entries will be used in the following way: A class is a solution if all its NEC table-entries are known and correct (ie. these entries are necessary before a class can become a solution), while the POS table-entries can be unknown, but if they are known, their value must be correct (ie. these entries are possible for a class, but not necessary).
When a method interprets all the table entries as NEC , and none as POS ), it will achieve formula (1). In order to achieve (2) it would have to interpret all table entries as POS . Any position in between (1) and (2) is possible by interpreting some attribute-value pairs as POS and others as NEC . The corresponding functionality consists of a combination of formula (2) for all POS table-entries and formula (1) for all NEC table-entries. This gradual transition from (1) to (2) will lead to an increase in possible answers for any given set of observations.
A practical use of such a mixed functionality would be to interpreted
the class-specific attributes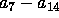 
as NEC for their corresponding classes, while interpreting all other table-entries
as POS .
We can relate this example to the notions discussed in the previous sections as follows:
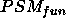: find classes that satisfy
(1) for all NEC table-entries, and
(2) for all POS entries.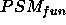
,
making this teleological requirement of type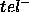 
)
,
it aims at reducing the incomplete answers produced by the PSM. (ie. such
an answer lies inside the goal-statement but outside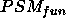 
)
Therefore this simple example already cannot be captured in the framework
of BFS96.
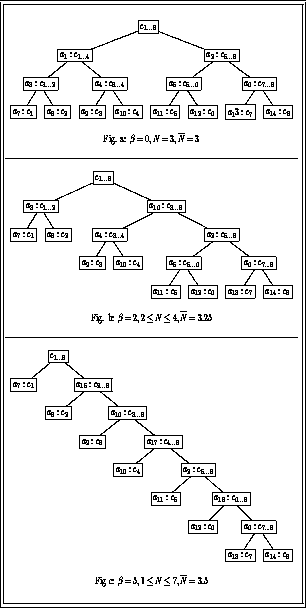
Figure 5: Differently balanced trees for the classification problem
from figure 4
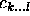stands for the disjunction of classes 
,
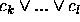indicating that these are classes sharing a set of attributes. In general,
such a hierarchical structure among the classes is domain specific, and
will be uncovered as a result of modelling the corresponding domain knowledge.
Obviously, the hierarchical relations among 
are a stylised example, but our results also holds for less idealised hierarchies.
In contrast to the previous example, in this example we will exploit
particular properties of a specific method, while the example from the
previous section was only concerned with the functional characterisation,
and not with the operational description. The following sketches a simple
classification method that exploits the hierarchical structures in figure
5 (the notation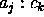 
in figure 5 means that observing attribute 
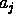is required at node 
):
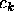P := top repeat C := child of P observe attribute at C if observation = table-entry then P := C else P := sibling(C) until P is a leaf return P(Notice that this method assumes definite answers to any observation. We assume that the answer unknown is never given). The following trace illustrates this method in figure 5-a.
.
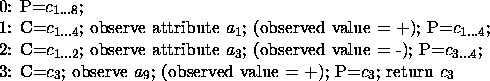
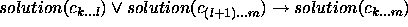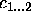is ruled out, avoid investigating 
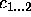's
children.
.
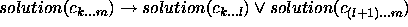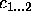is ruled out, immediately investigate the children of 
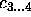without asking 
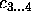's attribute.
.
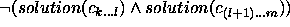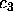has been
found as a solution, do not investigate alternatives.The number of questions that a method needs to ask during the classification
process can be incorporated as part of the goal-statement, e.g. that it
should be less than a given number, or that it should be as low as possible,
or that it should be as low as possible on the average, etc. The degree
to which such a goal is obtained depends on the quality of the domain knowledge.
In particular it depends on how well balanced the tree is. The balance
of the tree is a quality measure of the domain knowledge. The idea of a
balanced tree is that the children are equally distributed in the left
and the right subtree. A tree is balanced if the right and the left subtree
differ at most 1 in the number of their children. A tree becomes more unbalanced
when the differences between the number of children in the left and right
subtrees increases. The following function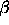 
is a measure of how unbalanced a tree is (ie. a higher number indicates
less ideal domain knowledge):
.
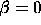This measure indicates the strength of the domain requirement that a tree
must balanced. The relation between the strength of this domain requirement
and the actual number of questions required is as follows (n is
number of classes (in our example n=8), b is the branching
factor of the tree (ie. the number of values per attribute, in our example
b=2), N is the number of questions required, and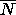 
is the average number of questions required, assuming equal a priori probability
of all classes).
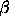-measure
that can be achieved in the domain.
).
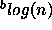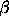-measure)
will increase the number of classes for which the goal can be obtained
(namely classification with at most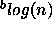 
observations). This will result in a reduction of both 
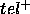and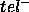 
. For example, in the
unbalanced tree in figure 5-b, the functionality
``establish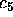 
in 4 questions''
is inside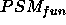 
but outside
the goal (since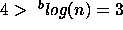 
), and
therefore it is in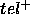 
). Correspondingly,
the goal statement ``establish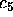 
in 3 questions'' is outside 
,
and therefore in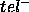 
. Increasing
the ontological requirement moves both the first statement outside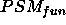 
and the second statement into 
,
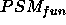thereby increasing the intersection of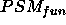 
and goal.
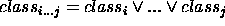. During the
descent of the abstraction hierarchy, this candidate set is gradually decreased,
until a single candidate remains. When the abstraction hierarchy is better
balanced (has a lower value for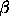 
),
this reduction of the candidate class happens faster. The average reduction
per observation is by a factor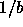 
in a balanced tree (ie. exponential reduction of the candidate set by 
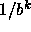after k questions) while in the least balanced tree 5-c,
the decrease of the candidate set is only linear (reduction by k
candidates after k questions). In this case, the ontological requirement
is again the balance of the abstraction-hierarchy, and the teleological
requirement is the amount of spurious candidates still in the candidate
set.
,
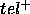while incompleteness (ie. missing answers) corresponds to a non -empty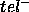 
in formula (5).
As pointed out in the literature, there are two ways of bridging the
gap between the functionality of a PSM and the intended goal: either by
increasing the functionality of the PSM by adding stronger domain-knowledge
(corresponding to increasing the ontological assumptions ont), or
stating that the unintended or unachieved answers are acceptable (corresponding
to increasing the teleological assumptions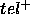 
and 
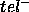respectively).
In the literature it has been pointed out that the ontological and teleological requirements can be interchanged, in the sense that strengthening one category allows weakening of the other, and vice versa.
We have pointed out that both ontological and teleological requirements can often be phrased in gradual terms instead of yes/no terms. We can often give a precise characterisation of the exchange relation between the different types of requirements. This allows us to deal with PSM that partially fulfill certain requirements. In other words, we are not restricted to reasoning about PSMs that do or don't fulfill a given requirement, but we can reason about the degree to which a PSM fulfill the requirement.
We have illustrated these ideas using simple classification PSMs whose functionality increased gradually depending on the gradual increase of the strength of the attribute-class relation, and on the gradual improvement of the quality of a classification hierarchy.
We claim that such a gradual characterisation of PSMs is useful for a number of different purposes:
Secondly, following the trail blazed by [Fensel
& Schoenegge, 1997] we should try to give machine assisted formal
proofs of such gradual characterisations of PSMs. Thirdly, our characterisations
should be tested in the context of large libraries of methods as described
in [Motta & Zdrahal, 1998] and
[Benjamins, 1994]. A final, but much
more theoretically difficult point is to find a good way to treat dynamic
properties of PSMs. In section 6
we were characterising the number of observations that a PSM required during
its problem solving, by encoding this dynamic property as part of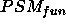 
and the goal statement. For other dynamic properties (such as anytime
behaviour of PSMs) such an encoding would be much more difficult, and a
more explicit treatment of dynamic properties (as opposed to the functional
I/O-relation) would be needed.
