Pascal Beys1,2, V. Richard Benjamins1 and Gertjan van Heijst1
In current knowledge engineering approaches for developing knowledge-based systems (KBSs), a KBS is viewed as consisting of separate but strongly interconnected components [Schreiber et al., 1994,Steels, 1990,Puerta et al., 1992]. These approaches, which are in contrast with viewing a KBS as a large set of rules, have considerably facilitated KBS construction and maintenance. Typically, components of a KBS include domain knowledge, inference knowledge and control knowledge. Inference and control knowledge can be packed together in so-called problem-solving methods (PSMs).
Although the construction of KBSs has been strongly facilitated by these approaches, building a KBS from scratch still appears to be a daunting exercise. Moreover, because there is a tendency to develop more and more complex KBS applications, the knowledge engineering task will even become more difficult. Therefore, we expect that, in the near future, KBSs (and in general, information systems) will be configured from reusable parts. For this reason, `reuse' is an important issue in both the software and knowledge engineering community.
In the knowledge engineering community, approaches such as CommonKADS [Schreiber et al., 1994], PROTÉGÉ [Puerta et al., 1992], VITAL [O'Hara et al., 1994], KACTUS [Schreiber et al., 1995] aim at enabling reuse of parts of a KBS. Candidates for reuse include problem-solving methods (abstract representations of the reasoning process) and domain knowledge.
It is obvious that the potential benefits of reusing existing domain knowledge are high if one takes into consideration that the amount of knowledge already represented in existing knowledge bases appears to be very large. For instance, in the KACTUS project [Schreiber et al., 1995], a domain that had been defined for a diagnosis purpose, is reused for a service-recovery purpose. In this paper, we focus on reusing domain knowledge, originally represented in the context of a particular PSM (or task), for another PSM. Such reuse requires that we have to link the terms of the ``new'' PSM with the terms of the domain knowledge. We will demonstrate the importance of assumptions [Gennari et al., 1994,Benjamins & Pierret-Golbreich, 1996,Benjamins et al., 1996,Fensel & Straatman, 1996,Fensel, 1995] and ontologies [Gruber, 1993,van Heijst, 1995] in establishing this link.
Most work on reuse has dealt with reuse in a task-specific context. See for example [Breuker & van de Velde, 1994], where reusable components are specified per task (e.g., planning, assessment, etc.), and [Benjamins, 1993], where an extensive library with PSMs for diagnosis is described. Recent work has, however, shown that PSMs for different tasks can be quite similar in spite of some apparent first differences [Breuker, 1994,van Heijst & Anjewierden, 1996]. This raises the question whether it is possible to enlarge the reuse scope of problem-solving methods across different tasks.
In this paper, we will investigate this question through so-called task-neutral problem-solving methods (TN-PSMs). TN-PSMs are context free methods in the sense that they do not use terminology that refers to a specific task. However, it is well known that describing a reasoning process at a more general (i.e., more reusable) level, diminishes its applicability (i.e., usability) [Klinker et al., 1991], because the distance between the reusable component and the domain knowledge at hand becomes larger, and thus establishing a mapping between them becomes harder. The aim of this paper is to remedy this tradeoff between reusability and usability. Our solution consists of partially automating the establishment of the mapping between a PSM and the domain knowledge that it uses. Since we use a syntactical approach, a domain expert is needed for interpretation in case several mappings are found, and for explicating properties of the domain knowledge when necessary.
The structure of this paper is as follows. In Section 2, we define the framework of this article. In Section 3, we briefly explicate the notion of domain ontology in the context of reuse. In Section 4, we introduce task-neutral PSMs, and in Section 5, we show how we can semi-automatically establish the mapping between the domain knowledge and the PSM. Section 6 points out related work and in Section 7, we present some conclusions. Throughout the paper, our approach is demonstrated with an example in the family domain.
In this section, we describe the framework of our approach. Although some terms are to be defined more precisely later (like domains in Sections 3 and methods in Section 4), we want to make clear the general background and the objectives of this paper.
A task describes a goal that must be achieved. Diagnosis is an example of a task, and a goal could be to find all causes that explain the observations. Tasks can be general (for instance planning) or specific (for instance select hypothesis), and can be decomposed recursively into sub-tasks.
A method or PSM describes how to achieve a task by decomposing it into subtasks and/or inferences, and specifying control knowledge. Inferences can be viewed as basic operators on knowledge and are applied on roles. Roles are views on the domain knowledge where the PSM is applied. Control knowledge defines the ordering of the operators. PSMs can be general (e.g., generate and test) or more specific (random-select-fix). PSMs, as they are used in current research, are task-dependent, that is, their use is restricted to a particular task. Such PSMs can be organized in libraries, where a collection of (alternative) PSMs is associated to a particular task. In these libraries, the relation between tasks and PSMs is a one-to-many relation.
Domain models describe the actual knowledge of the domain. Domain ontologies provide the vocabulary for expressing domain models and put constraints on their structure. Typically, domain models contain ground sentences. Domain knowledge is the union of domain ontologies and domain models.
The contribution of our work is concerned with:
The situation considered in this paper is that we want to reuse domain knowledge already represented for a specific application, for a different purpose. In other words, we are concerned with reusing domain knowledge originally represented for one PSM, for a different PSM. Furthermore, we are concerned with PSMs that are reusable across different tasks.
An ontology can be viewed as an explicit knowledge-level specification of a conceptualization [van Heijst, 1995]. Ontologies can be viewed as meta-models of the actual domain knowledge. To formulate ontologies, we make use of the vocabulary defined in Gruber's Frame Ontology [Gruber, 1993]. The Frame Ontology defines 63 meta-predicates that can be used to characterize classes, relations, functions (attributes) and instances. Table 1 shows some of the Frame Ontology predicates used in this paper.
Table 1: A selection of Frame Ontology predicates along with
their definitions.
Figure 1 shows the ontology of the family domain example, which will be used throughout the paper. A member of a family is called a person and can be either of type ancestor or child. Instances of person are inter-connected via descendancy, a binary relation. The instances of child do not have descendants and constitute the leaves of the person tree. Each ancestor is associated to a country through the has nationality binary relation. Each child is connected to his brothers and sisters by the sibling relation and is associated to his place of birth via the born in relation. A place is associated to the country it lies in.
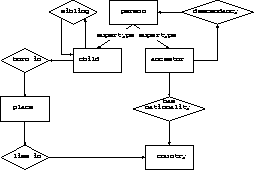
Figure 1: The family domain at the ontology level. Rectangles denote
classes and diamonds binary relations.
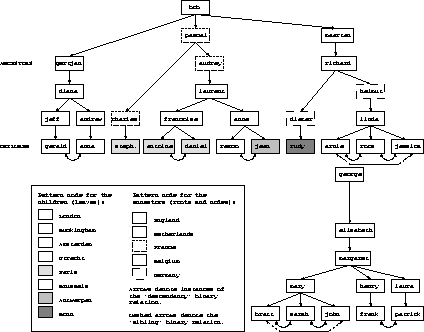
Figure 2: The family domain at the domain-model level.
Originally, this domain was used for finding the nationality of ancestors of children. The new purpose, which will be used as an illustration throughout the paper, concerns the generation of all possible paths linking a child to a country. For this new purpose, the class place and the binary relations born in, lies in and sibling have been added to the ontology.
A domain model describes the actual state of affairs in a particular
domain. It consists of sets of tuples that are formulated in the
vocabulary defined in the ontology and that satisfy the constraints in
the ontology. Figure 2 illustrates the domain model
of the family domain consisting of two families which uses the classes
and binary relations described in the ontology
.
In this section, we will briefly resume PSMs as they are currently viewed in work on knowledge engineering, then point out some of their problems for reuse, and finally introduce task-neutral PSMs.
Most of the PSMs presented in the literature are described in the context of a specific task, that is, their description uses task-specific terminology. To describe such task-specific PSMs, we adopt the approach taken in [Fensel & Straatman, 1996,Benjamins et al., 1996] where a PSM consists of three interrelated parts as illustrated in Figure 3.
Figure 3: The parts of a problem-solving method (taken from Benjamins,
Fensel and Straatman, 1996).
The description above is of a so-called ``composite'' PSM, that has an internal specification. There are also ``primitive'' PSMs, that do not have an internal (operational) specification.
There are two factors that hamper the reuse of PSMs across domains and tasks: the interaction problem [Bylander & Chandrasekaran, 1988] and what we call the task-dependency problem.
The interaction problem can be circumvented by making the dependencies between PSMs and domain knowledge explicit (the explicit interaction principle [van Heijst, 1995]). Assumptions of PSMs capture exactly this feature: they are explicit statements about what a PSM expects from the domain knowledge. This does, however, not solve the task-dependency problem. In our context, this problem manifests itself in two ways:
This is the reason why reuse of PSMs is usually limited to the task for which they were originally specified. To cope with this problem, we introduce task-neutral problem-solving methods (TN-PSMs).
Task-neutral PSMs are similar to normal PSMs, with the difference that the functional and operational specifications and the assumptions are formulated in task-neutral terminology. TN-PSMs can be associated to several tasks.
Van Heijst and Anjewierden vanHeijst:96a showed how to formulate the operational and functional specification of a PSM in task-neutral terms, as is shown for the PSM cover in Figure 4.
[Benjamins & van Heijst, 1996] demonstrated that it is possible to characterize domain models in terms of Gruber's Frame Ontology [Gruber, 1993] (which is task-neutral), in such a way that these domain characterizations can be referred to in the assumptions of PSMs. In other words, assumptions can also be formulated in a task-neutral way. It turned out that the relations typically used in device models of physical systems (e.g., structural, topological, causal model) can be adequately characterized by the Frame Ontology. This implies that, if two relations can be characterized by exactly the same assumptions, then they are identical from the PSM's point of view, regardless of the fact that in the real world they are considered as being different.
As task-neutral functional and operational specifications are merely syntactical, the implicit references to the task that are normally semantically expressed in task-dependent PSMs (for instance, a reference to `hypothesis' in a PSM for diagnosis) disappear. Therefore, the knowledge manipulated by the operational specification of the PSM has to be made explicit. To this end, we distinguish between two kinds of task-neutral assumptions (see also [Benjamins & Pierret-Golbreich, 1996]).
Figure 4: Task-neutral description of the PSM cover. This version of
cover aims at finding for a set of leaf nodes all root nodes to
which it is connected through a directed graph structure.
The control structure of cover can be described as follows: for each leaf node, we apply the find-neighbor inference that computes the set of neighbors to which the leaf node is connected, via any binary relation xi in X defined in the structure assumption. If this set of neighbors is empty, find-neighbor will assign the leaf the root role. If the set of neighbors is not empty, then root is empty (the node under study is not a root). We then add the set of neighbors to the set of leaves diminished by the leaf just processed (we also remove duplicates by using the union inference). Finally, we add the root (that can be empty) to the cover set, and we loop until the set of leaves is empty.
Cover has several property assumptions. Its control structure assumes
that there are no cycles in the graph. Cycles only occur when two
classes linked by a binary relation are the same (denoted as if
Ai-1=Ai
in Figure 4). In that case, the property
assumptions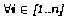 
asymmetric
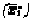, (which
means that the deductive closure of each x that constitutes X is
asymmetric) and 
irreflexive(xi) become necessary.
Furthermore, transitivity is also required for binary relations
linking the same classes in order to assure access to all intermediate
states (for instance descendancy requires transitivity to access
all descendants of an ancestor that are themselves
ancestors). Finally, the composite binary relation X needs to be a
one-to-many relation to insure a tree structure. For a precise meaning
of the assumptions, see Table 1.
In this section, we have suggested how to enhance the reusability of a PSM by introducing TN-PSMs. Consequently, TN-PSMs have a larger distance to the domain knowledge than normal PSMs. Thus, on the one hand, we are now able to reuse TN-PSM across a range of tasks, but, on the other hand, the effort needed to map the TN-PSM to a specific domain has increased. The latter would, in practice, destroy the advantages of a wider reuse; after all, reuse is only interesting if the effort to apply reusable components in a new situation is less than the effort for building the components from scratch. In order to deal with this problem, we propose, in the next section, an approach to partially automate the construction of the mapping between a TN-PSM and domain knowledge.
In this section we will investigate to what extent it is possible to automatically find a mapping between a given TN-PSM and given domain knowledge. We assume that a user (domain expert or knowledge engineer) has selected a TN-PSM to achieve a goal, and wants to verify whether it is applicable to a particular domain knowledge. We assume that the mapping from the goal (expressed in task and domain dependent terms) to the competence of the TN-PSM can be established. In our example, the goal is to find all possible relations linking a child to a country.
Linking a TN-PSM to domain knowledge consists of satisfying the assumptions of the TN-PSM in the domain knowledge. As mentioned in Section 4.1, TN-PSMs, like normal PSMs, can be recursively decomposed into other, more specific TN-PSMs until primitive PSMs are reached. The assumptions of a composite TN-PSM are formed by the conjunction of the assumptions of its constituting primitive PSMs and inferences. Therefore, we have to satisfy each assumption separately in order to satisfy the global PSM assumptions. Two issues can be distinguished for linking TN-PSMs to domain knowledge.
Figure 5: Structure assumption of the PSM cover. Rectangles denote
classes and diamonds binary relations.
The mappings that pass the two steps above, give the possible mappings of the TN-PSM to the specific domain. In the following section, we explicate how this two-step procedure is performed.
Our aim is to apply the PSM cover (shown in Figure 4) to generate all possible paths linking child and country in the family domain. When we look at the structure assumptions (Figure 4), we see that we need a sequence of binary relations where the arguments are classes, and the input class is a set of leaves and the output class is a set of roots.
First, we manually map the input/output of the structure assumptions
of our method onto the domain. In our example, this corresponds to
mapping A0 to the class child, and An to
the class country (see the structure assumptions
A0 = set of leaves and An = set of roots in Figure 4).
The structure assumption 
[1..n-1] class(Ai)
is trivially true in our example. The last part of the structure
assumption concerns to find a binary relation. For this, we
automatically search at the ontology level for structures that are
equivalent to the structure assumptions of the TN-PSM. This search is
performed through equivalence operators that can establish structural
similarities between the structure assumptions and the ontology (which
are both expressed using the Frame Ontology). Examples of such
operators are described in Table 2.
Table 2: Examples of operators to search for equivalent
structures in the domain ontology.
Our structure assumptions, domain knowledge and equivalence operators are implemented in Prolog, and consequently we use Prolog's search strategy. All applicable operators are tried out onto the structure assumptions until a structure is derived that matches the domain ontology level. The solution defines the mapping process. If no solutions can be found, this means that it is impossible to create a mapping from the TN-PSM to the knowledge available at the ontology level. The matching process is implemented by a graph search. It is possible that several solutions are found, which means that there are several ways to derive the part of the ontology structure under study from the structure assumption.
Since our approach is syntactical, the interpretation at the domain model level of that construction, does not consider the meaning of the different binary relations composing that construction. All instances of these binary relations are thus seen as instances of the constructed binary relation.
In the family domain, the graph search algorithm finds nine candidate structures:
An example of the trace of the application of the equivalence operators leading to the discovery of structure 5 is given in Figure 6.
Figure 6: Trace of a succesful application of a
series of operators to determine a binary relation between child and
country. The search is for the moment performed in Prolog.
Once the structure assumptions have successfully been matched to the domain ontology resulting in one or more candidate structures, we have to verify the property assumptions on them. There are two ways to perform this verification:
In our implementation, we use the following strategy: if a property cannot be verified at the ontology level, it is checked in the domain model. If this cannot be done automatically, a question is posed to the domain expert or knowledge engineer.
To illustrate the above, consider how the set of candidate-structures in the family domain can be reduced by taking the property assumptions into account. One of the property assumptions of cover is that each of the binary relations composing the candidate-structure should be asymmetric. In the family domain, sibling has been declared to be symmetric at the ontology level ( if sibling(arnie, roos), then sibling(roos, arnie). Any composition of binary relations using sibling should consequently be dropped. This leaves us with three possible structures (structures 1, 5 and 6). Figure 7, 8 and 9 graphically show these remaining candidates.
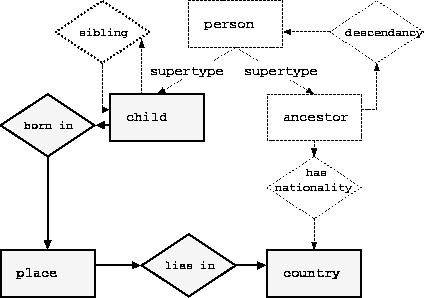
Figure 7: First remaining candidate-structure.
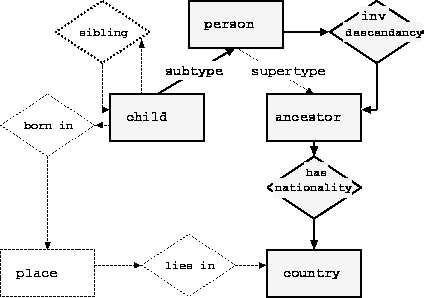
Figure 8: Second remaining candidate-structure.
Figure 9: Third remaining candidate-structure.
Due to the syntactic nature of the mapping, we may find several of them, as is the case in the family domain. However, we expect their number to be small because of the constraints (both properties and structures) that are applied. Nevertheless, if several valid mappings are found, we have to understand the meaning of these different mappings. This analysis may take place at the ontology level and at the domain model level. In addition, in case no mapping can be found, we can analyze the reason of failure. We will now briefly describe each of these forms of analysis.
When mappings are partially overlapping through their structure, they express, at the ontology level, variations in the reasoning process within the same method. This can be related to optimization, for instance the shortest path could be defined as being the most optimal.
When mappings are essentially disjoint, they express a different interpretation of the domain knowledge, still within the same method. For instance, when two disjoint paths link two classes, this expresses two different ways of reasoning and only the domain expert can choose which one holds (or if both hold). In the family domain, the mappings in Figure 7 and Figure 8 and in Figure 7 and Figure 9 are disjoint. The mappings in Figure 8 and Figure 9 are overlapping.
For a further analysis of the mappings, we can apply the mapped method on the knowledge base and have a domain expert interpret the results.
Table 3: Results of [born_in], [lies_in]. This relation is a one-to-one
relation, that links a child to a country via the place it is born
in.
Table 4: Results of [subtype, [child,person]], [inv,descendancy],
[has_nationality]. This relation links a child to a country via the
nationality of his ancestors.
Tables 3 and 4 present the instances obtained by applying cover on the first two remaining candidate-structures (respectively Figure 7 and 8), which represent two ways to link child to country. Both are valid, however disjoint and different. The first one is a one-to-one relation whereas the second one is a one-to-many relation. They do not express the same thing. At this point, a domain expert is necessary to interpret these two relations. The first one links child to country through the born in and lies in relations. This relation can therefore be interpreted as giving the nationality by using the `soil-law' relation. The other relation links child to country via the nationality of the ancestor. This relation can be interpreted as a `blood law' relation giving the nationality of a child according to the nationality of his parents.
The third candidate structure (Figure 9) does not yield any result, because in the definition of our domain model we implicitly described the subtypes child and ancestor as being disjoint. Thus, there are no instances of person that both belong to the child subtype and to the ancestor subtype and the path [subtype,[child,person]], [supertype,[ancestor,person]] does not hold any instance. The Frame Ontology allows to describe mutually disjoint subtypes, but the description of our ontology did not originally use that definition. Notice that, had we declared these subtypes as being disjoint in the ontology, we would have had to update our list of operators in such a way that any sequence supertype, subtype of disjoint subtypes would be forbidden. Consequently, structures 4, 6 and 9 (see Section 5.1) would have already been filtered out in step 1.
In general, if no mapping can be found, the TN-PSM is not applicable in that domain knowledge, and an alternative TN-PSM has to be considered. However, the reason for the failure to find a mapping can hint at several interesting things.
. In
this way, the user can decide whether the result is acceptable or
not.
One of the underlying ideas of our work dates back to Clancey's work on Heuristic Classification (HC) [Clancey, 1985]. Clancey analyzed a variety of expert systems in different domains (i.e., MYCIN: medical diagnosis, SACON: program configuration, GRUNDY: book selection, SOPHIE-III: diagnosis of electronic circuits), and showed that each of them uses the heuristic classification method. In our terminology this means that HC is considered as a PSM with its assumptions, and that each of the different domains, albeit very different, satisfy these same assumptions. It would be an interesting endeavor to make the assumptions of HC explicit and to check whether the different domains do actually satisfy them.
The distinction between task-dependent and task-neutral PSMs bears similarity to what is called in [Aben, 1995] the teleological view versus the operational view of classifying inferences. According to the teleological view, inferences are characterized in terms of the goal they are supposed to achieve, and are thus task dependent. According to the operational view, inferences are characterized in terms of the operations they perform on domain knowledge, using an ontology-oriented terminology. Thus, they are task-neutral.
In [Benjamins & Pierret-Golbreich, 1996], a framework for characterizing assumptions of PSMs is proposed. Three main categories are distinguished being: epistemological, pragmatic and teleological assumptions. The epistemological assumptions are further divided into availability and property assumptions. The structure and property assumptions, we introduced in this paper, correspond to the availability and property assumptions. The availability/structure assumptions describe that some knowledge types need to be available, whereas the property assumptions describe characteristics that the knowledge should possess. Pragmatic and teleological assumptions are not considered in this paper.
The work described here bears similarity to subfields of Machine Learning [Michalski et al., 1986], in particular to Explanation-Based Learning and ``Inductive Logic Programming'' [Lavrac & Dzeroski, 1994]. In this paper, we are concerned with automating the mapping between a task-neutral PSM and a particular domain. The first step of the mapping is established through a search for a match between the structure assumptions of the PSM and the ontology that describes the domain knowledge. The structure assumptions of the PSM describe a particular relation that needs to exist in the domain ontology. A successful result of the matching process means that such a relation can be constructed from the relations available in the domain ontology. In other words, we have learned a ``new'' relation in the ontology that previously was not explicitly there, although it implicitly existed. In this learning process, the structure assumptions of the PSM served as a filter or bias.
In another part of this paper (Section 5.2), we mentioned
that at the domain-ontology level we can declare certain
characteristics of domain relations. For instance, we stated at the
ontology level that the relation sibling is symmetric. This
prevented us from checking the sibling relation for symmetry for each
of its domain instantiations. Moreover, for redundancy reasons, it is
also better to represent such characteristics at the ontology, rather
than extensively in the domain knowledge. A subfield of Inductive
Logic Programming (ILP) is concerned with learning from databases that
certain relations have certain characteristics. For instance, once an
ILP algorithm has shown that each instance of a certain relation is
symmetric (e.g.,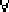 
x,y
rel(x,y) = rel(y,x)), it suffices to
represent only rel(x,y) and represent at the ontology level that
rel is symmetric. All rel(y,x) can then be deleted. This leads to
a more parsimonious database that contains, however, the same
information. We foresee that we can use techniques from ILP to
inductively learn characteristics of relations in the domain knowledge
and then represent them at the ontology level. This would make the
process of automatically constructing the mapping more efficient.
In this paper, we showed how the reusability of problem-solving methods can be enhanced such that they can be reused across different tasks, as opposed to within a specific task. To this end, we introduced task-neutral PSMs which are described in a task-neutral terminology (Frame Ontology), and are thus not related to a specific task such as for example diagnosis, planning, assessment, etc. TN-PSMs have a larger distance to domain knowledge, which means that their usability is lower than that of task-dependent PSMs. We proposed an approach to alleviate this problem by partially automating the mapping from a TN-PSM to the domain knowledge to which it has to be applied. This mapping process exploits two kind of assumptions (which are also neutrally described): structure assumptions, which describe the ontological structure of the knowledge needed by the TN-PSM, and property assumptions, which relate to the types of inferences allowed by the ontology.
These structure assumptions form the core of our approach since the construction of the mapping is based on a search (by operators) in the domain ontology for equivalent structures that can satisfy the structural assumptions. Due to the syntactic nature of our approach, several mappings might be found. As a matter of fact, one can hardly expect to use neutral terms and to obtain the exact interpretation wanted by the domain expert. Nevertheless, the set of constraints specified in the property assumptions of the TN-PSMs is expected to limit the amount of possible mappings created. The remaining mappings have to be interpreted by a domain expert.
We have shown an example of automatic creation of a mapping between the TN-PSM cover and the so-called family-domain. In the example, we obtained two possible mappings with different interpretations. In this context, the question to the meaning of several mappings arises. Can the need for an expert be regarded as the ``re-manifestation'' of the usability problem? This would be the case if there were so many different mappings generated that interpreting them would be too large an effort. In this paper, we demonstrated that, at least in our example domain, the structure assumptions and the operators to match them to the domain ontology, as well as the property assumptions, keep the number of mappings limited. Further research is needed to see how the approach scales up.
As was already mentioned, our goal is to maximize reusability without sacrificing usability, by automating the mapping process. The experiment we performed showed that this is possible, but not that it is feasible. The quality and number of the generated mappings depends heavily on our ability to explicate assumptions of PSMs and properties of ontologies, and to do this in a task-neutral terminology. We view this as an important challenge for current knowledge engineering research.
We thank Bob Wielinga and Maarten van Someren for their helpful and inspiring discussions. We also thank Ameen Abu-Hanna for his comments. This research has been conducted in the context of a cooperation between the University of Amsterdam and the University of Pierre et Marie Curie. It was partially supported by the Netherlands Computer Science Research Foundation with financial support from the Netherlands Organisation for Scientific Research (NWO).
Remedying the Reusability -- Usability Tradeoff for Problem-Solving Methods
This document was generated using the LaTeX2HTML translator Version 95.1 (Fri Jan 20 1995) Copyright © 1993, 1994, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -show_section_numbers -split 0 setup.tex.
The translation was initiated by Richard Benjamins on Thu Sep 26 14:46:05 MET DST 1996
