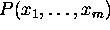 .
More formally, for each state variable
.
More formally, for each state variable 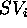 , DDL.1 allows the
specification of:
, DDL.1 allows the
specification of:
Amedeo Cesta1 and Angelo Oddi2
Recent results in planning research have clarified several basic mechanisms involved in problem solving activity specialized to planning ---see [Chapman, 1987,Pednault, 1989,Bäckström, 1992,Kambhampati et al., 1995] and many others. Several planning systems have been applied to practical problems (e.g., SIPE [Wilkins, 1990], O-PLAN [Currie & Tate, 1991], OPIS [Smith et al., 1990], and HSTS [Muscettola et al., 1992]). The planning community has devoted several efforts to filling the gap between theoretical and application-oriented work, examples may be the Zeno planner [Penberthy & Weld, 1994] on one side and Tate's <I-N-OVA> formalism [Tate, 1995] on the other. This middle-ground work has the aim of both dealing with more complex domains and following a well-founded approach that allows the generalization of results.
Further work is needed in a knowledge engineering perspective to cope with the problem of building up knowledge-based planning systems that are validated enough to be delivered as complete applications. From the last standpoint, Knowledge Acquisition (KA) techniques may usefully integrate the current planning research in the design of engineered planning systems. KA's techniques are being applied to two different aspects of the planning problem:
The present work refers to the second approach and aims at presenting a formal language useful to describe relevant aspects of a planning domain. The domain description is a fundamental initial step to address both planning and scheduling problems. Knowledge-based domain independent planners are endowed with a Domain Description Language (DDL); a knowledge representation language that allows users to specify the basic components of a domain, to associate a description to those components and to specify the constraints and mutual relationships among components. Our efforts may be summarized in the aim to build a language that:
In our view, some aspects first proposed in the HSTS [Muscettola et al., 1992,Muscettola, 1994] domain description language are of interest for our aims because:
In this paper we propose a representation language named DDL.1, that uses the same ontology of the HSTS-DDL, but it is restricted in its expressive power in order to develop a clear semantics and to specify a temporal planner that exploits the formalized aspects of the language. Although the used ontology exploits ideas from control theory [Kalman et al., 1969] we propose here a formal account that refers to classical AI studies for describing both the semantics of the language and the planning process.
The paper is organized as follows: Section 2 introduces the features of DDL.1 language. Section 3 depicts more specifically the way of defining constraints in DDL.1 and presents the language complete syntax, while Section 4 presents its semantics. Sections 5 proposes a temporal planner that actually uses the formalism. Section 6 discusses related research while Section 7 concludes the paper.
DDL.1 representation adopts basic ideas from control theory
[Kalman et al., 1969,Dean & Wellman, 1991] extended to allow the specification of
constraints. The planning problem is seen as the problem of deciding
the behavior of a dynamic domain. The behavior of a domain (its
temporal evolution) is seen as the continuous interaction among
different components. Each domain component is represented using
state variables; a single state variable (SV) is a relevant
feature of the component. DDL.1 allows the intensional description
of any plausible temporal evolution of the state variables. Such
evolution is defined describing the set of values a SV may
assume over time, and a set of constraints, named
compatibilities, a value should satisfy when assumed by the related
SV. In DDL.1 state variables' values are restricted to a discrete
set and are instances of predicates of the form 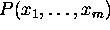 .
More formally, for each state variable
.
More formally, for each state variable 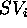 , DDL.1 allows the
specification of:
, DDL.1 allows the
specification of:
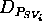 of the
value-predicates
of the
value-predicates 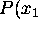 ,...,
,..., 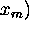 ;
;
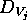 of each variable
of each variable 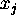 appearing in
the value-predicates;
appearing in
the value-predicates;
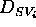 of the state-variable
values can be defined.
of the state-variable
values can be defined. 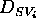 is the set of the ground terms
obtained by substituting the variables in
is the set of the ground terms
obtained by substituting the variables in 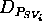 with the
domain values
with the
domain values 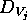 .
The dynamics of a state variable
.
The dynamics of a state variable 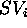 is defined as the
set
is defined as the
set 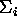 of all the functions
of all the functions
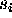 :
: 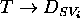 where T is the discrete set of time instants. Given the definition
of each SV, the set
where T is the discrete set of time instants. Given the definition
of each SV, the set 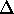 of the domain evolutions may be
defined as:
of the domain evolutions may be
defined as:
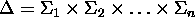 .
.
By defining compatibilities DDL.1 allows the user to represent
constraints on the legal sequences of values that a state variable
may assume over time. A given value may be constrained by different
values on the same state variable, and by values on different state
variables. Those further constraints express the domain theory,
namely the description of the domain laws in terms of reciprocal
adaptability, synchronization, and dependency relations among
values. By constraining the situations in which a given value may be
taken by a state variable a generic compatibility C represents
a restriction of the possible evolutions of the domain, that is 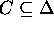 .
.
A (set of) goal(s) in this framework is the specification of a (set
of) ``desired" value(s) to be taken by SVs. Planning means
determining a particular temporal evolution (i.e., a function
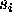 :
: 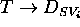 for each state variable
for each state variable
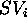 ) that satisfies both the goal(s) and all the specified
compatibility constraints.
) that satisfies both the goal(s) and all the specified
compatibility constraints.
A simple example from a process planning domain may help to show the
DDL.1 use. The domain consists of a drilling machine able to create
holes of two different diameters by automatically switching between
two different bits. The holes are executed when a piece of a certain
material is blocked on the support of the drill.
A domain model may contain two state-variables named: 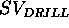 ,
that represents the operating status of the drilling tool, and
,
that represents the operating status of the drilling tool, and
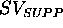 , that represents the operating status of the support.
The state-variables' dynamics is described defining the set of values
each SV may assume. In this case:
, that represents the operating status of the support.
The state-variables' dynamics is described defining the set of values
each SV may assume. In this case:
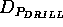 ={WAIT,
={WAIT, 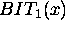 ,
, 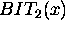 }.
WAIT represents an idle state,
}.
WAIT represents an idle state, 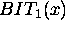 and
and 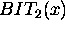 represent a status in which the machine is drilling a hole on the
piece x using different bits.
represent a status in which the machine is drilling a hole on the
piece x using different bits.
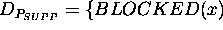 ,
, 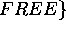 .
. 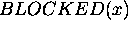 represents the fact that piece x is ready to be drilled on the
support.
represents the fact that piece x is ready to be drilled on the
support.
To sum up, a domain description that can be built by a DDL.1 specification contains state-variables, state-variable values, and compatibilities. Compatibilities allow the user to represent constraints on the legal sequences of values that a state variable may assume. A given value may be constrained either by different values on the same state variable, and/or by values on different state variables. A compatibility asserts an intensional constraint on the behavior of a state variable. Such constraint consists of two components: (a) a causal component that defines a causal relation between two values: a reference value and a constraining value; (b) a temporal component that specifies a temporal constraint on the causal component. The temporal relation may contain both a qualitative and a quantitative constraint. Table 1 shows the whole specification of the language. May be observed that the causal component of a compatibility are described by the syntactic categories <RefValue> (the reference value) and <ConstrValue> (the constraining value). The temporal component is specified by a restricted number of the qualitative temporal relations usually defined in the literature [Allen, 1991] (to simplify matters only the MEETS, MET-BY and DURING are allowed). The MEETS and MET-BY relations constrain two values belonging to the same state variable to appear in strict sequence in any legal behavior of the SV (namely, MEETS (MET-BY) states that the end-time (start-time) of the reference value coincide with the start time (end-time) of the constraining value). The DURING relation constrains two values belonging to different state-variables. It is used to express synchronization constraints between the state variables' behaviors (more specifically DURING states that the start-time of the constraining value precedes the start-time of the reference, and its end-time follows the end-time of the reference).

Table 1: BNF Specification of DDL.1
Following the syntax in Table 1 we can describe the
domain of the drilling machine according to the model previously
introduced. Legal value sequencing are described by using
compatibilities. Figure 1 shows the constraints
relative to the values of the 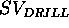 .
It is possible to observe some characteristics of the language:
(a) the first compatibility uses an OR-COMP to describe the
constraints on the value WAIT. It enumerate the possible legal
sequences that include WAIT, one of them should be verified on any
legal temporal evolution including WAIT. (b) With MEETS and MET-BY
constraints specification are specified to describe legal value
transition on the SV. For example, the second and third
compatibilities state the constraint that it is not possible to
execute two consecutive holes without intermixing a WAIT value.
(c) The DURING temporal relation is used to specify values
synchronization between two state-variables. Again, in the second
and third compatibilities of Figure 1, a DURING
specification states that it is possible to drill with BIT
.
It is possible to observe some characteristics of the language:
(a) the first compatibility uses an OR-COMP to describe the
constraints on the value WAIT. It enumerate the possible legal
sequences that include WAIT, one of them should be verified on any
legal temporal evolution including WAIT. (b) With MEETS and MET-BY
constraints specification are specified to describe legal value
transition on the SV. For example, the second and third
compatibilities state the constraint that it is not possible to
execute two consecutive holes without intermixing a WAIT value.
(c) The DURING temporal relation is used to specify values
synchronization between two state-variables. Again, in the second
and third compatibilities of Figure 1, a DURING
specification states that it is possible to drill with BIT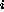 only
while a piece is BLOCKED on the support
only
while a piece is BLOCKED on the support 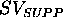 .
Compatibilities related to the
.
Compatibilities related to the 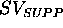 are not presented. The
only constraint contained in it states that a BLOCKED value should
be reasonably followed by a FREE one.
are not presented. The
only constraint contained in it states that a BLOCKED value should
be reasonably followed by a FREE one.

Figure 1: Compatibility constraints on the state variable
DRILL
For the sake of exemplification of single properties of the language, we have described a very limited behavior of the domain. It should be clear that the same language can be used for more fine-grained descriptions. For example it is possible to explicitly describe and represent the set-up times needed to arrive at different operating status of a certain represented instrument, etc. ---see [Muscettola et al., 1992,Muscettola, 1994] for several examples.
The language allows to represent quite complex aspects of the problem
domain:
(a) temporal evolutions of domain features: in fact, all the value
specifications are enriched with duration constraints for the
interval of time that a SV assumes the values. Durations are
represented by an interval 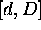 where d and D represent
minimal and maximal time length;
(b) physically realizable transition between values by the MEETS and
MET-BY specifications;
(c) different processes in the domain behaving in parallel by using
state variables;
(d) synchronization constraints between parallel processes by using
the
where d and D represent
minimal and maximal time length;
(b) physically realizable transition between values by the MEETS and
MET-BY specifications;
(c) different processes in the domain behaving in parallel by using
state variables;
(d) synchronization constraints between parallel processes by using
the 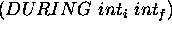 ;
(e) simple resource constraints: in fact, we can consider a resource
as described by a state-variable, and a value as a reservation on it
for a given interval of time. With the syntactic restriction given
here we can represent only binary capacity constraints ---extensions
are investigated in [Muscettola, 1994].
;
(e) simple resource constraints: in fact, we can consider a resource
as described by a state-variable, and a value as a reservation on it
for a given interval of time. With the syntactic restriction given
here we can represent only binary capacity constraints ---extensions
are investigated in [Muscettola, 1994].
An interesting aspect to notice is the intuitive and graceful methodology the language makes available to the user for describing the features of the domain. This methodology is made possible by having the state variables and their values as first class objects in the language at a symbolic level. Moreover, the compatibility specification allows to describe uniformly an interesting number of constraints governing the domain dynamics. Such constraints are also introduced using the uniform metaphor of the description language. More conventional languages may have a rather similar expressive power but have a representation metaphor different and less user-oriented. In our view, action-centered formalisms in general allow a description of a domain very atomic and not aggregated, not easily controllable by the user.
A further comment concerns the restricted use of qualitative temporal relations done in the language. The purpose of the paper was to show the main idea of the specification of constraints that frame state-variables evolutions due to ``internal'' or ``external'' causal effects. The three temporal relation described are enough for the purpose. Extensions are possible, also in the semantics that follows, to include the usual complete set of relations.
The constraints stated by compatibility specification bound
the number of evolutions of the represented domain (the set
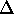 previously introduced).
The semantics of any language sentence is defined as the set
of the evolutions compatible with the
given constraints. To obtain a formal shape for such an intuitive
idea some preliminary definitions are needed.
previously introduced).
The semantics of any language sentence is defined as the set
of the evolutions compatible with the
given constraints. To obtain a formal shape for such an intuitive
idea some preliminary definitions are needed.
Considering the syntax in Table 1,
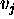 denotes an element belonging to the syntactic category
<Value> of the state variable
denotes an element belonging to the syntactic category
<Value> of the state variable 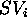 .
We designate with
.
We designate with 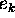 a ground element of a temporal evolution of the state
variable
a ground element of a temporal evolution of the state
variable 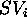 . It is worth noting that
. It is worth noting that 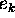 is a
3-ple:
is a
3-ple: 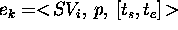 , where
, where
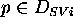 and
and 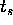 ,
,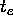
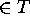 with
with 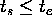 .
Given a function
.
Given a function 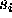 :
: 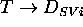 ,
an element of evolution
,
an element of evolution 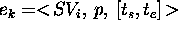 is contained in
is contained in 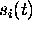 (denoted by
(denoted by 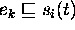 ),
if
),
if 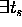 and
and 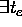 such that the function
such that the function
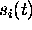 assumes the value
assumes the value 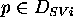 in the interval
in the interval
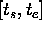 .
An element of evolution
.
An element of evolution 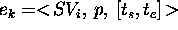 is contained in a value
is contained in a value 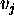 =
= 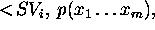
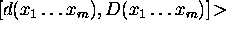 (denoted by
(denoted by 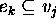 ) if a ground
instance
) if a ground
instance 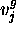 =
=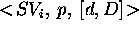 of
of 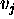 exists such that
exists such that 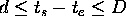 .
.
The DDL.1 semantics is defined by using the function:
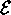 :
: 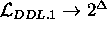 where
where 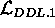 represents the set of sentences
allowed by the DDL.1 grammar and
represents the set of sentences
allowed by the DDL.1 grammar and 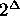 is the power-set of
is the power-set of
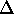 .
As said above, the semantics of a given domain description is
a subset of
.
As said above, the semantics of a given domain description is
a subset of 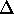 .
The subset can be obtained from the intersection of the sets
of temporal evolution allowed by each constraint of the
language (that is, by each compatibility). A function
.
The subset can be obtained from the intersection of the sets
of temporal evolution allowed by each constraint of the
language (that is, by each compatibility). A function 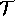 given a compatibility
c computes the subset of admissible evolutions contained in
given a compatibility
c computes the subset of admissible evolutions contained in
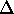 .
The function
.
The function 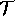 is of the kind
is of the kind
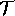 :
: 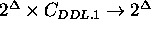 where
where 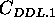 is the set of compatibilities that can be
defined using DDL.1.
is the set of compatibilities that can be
defined using DDL.1. 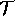 can be defined as follows
(where
can be defined as follows
(where 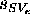 represents the temporal evolution s of the SV
in which the ground element e is assumed):
represents the temporal evolution s of the SV
in which the ground element e is assumed):
aaabbbbccc ¯
=
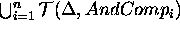
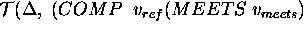
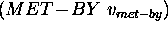
...
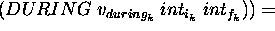
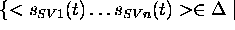
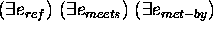
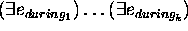
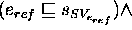
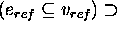
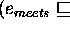
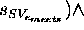
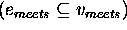
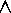
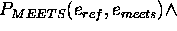
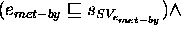
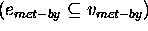
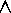
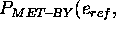
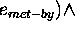
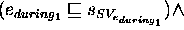
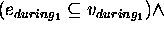
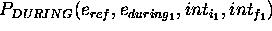
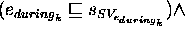
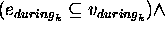
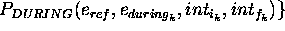
To complete the definition of 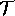 , a definition for the
temporal predicates
, a definition for the
temporal predicates 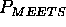 ,
, 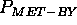 e
e 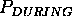 is
needed. Given any couple of elements
is
needed. Given any couple of elements 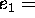
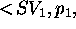
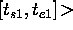 , and
, and
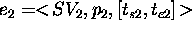 , and two intervals
, and two intervals
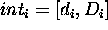 and
and
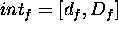 those predicates are defined as follows:
those predicates are defined as follows:
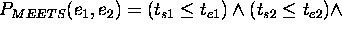
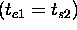
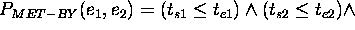
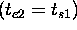
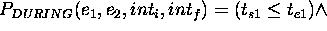
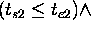
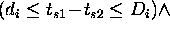
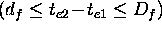
Finally the formal semantics 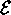 can be inductively defined
as:
can be inductively defined
as:
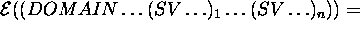
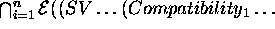
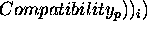
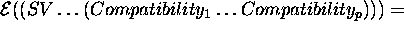
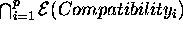
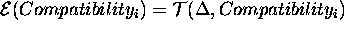
It is worth observing that according to this semantics when 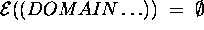 the domain description is
inconsistent.
the domain description is
inconsistent.
The previous Sections introduces a particular language to describe the constraints framing the evolution of a physical domain. This Section deals with the use of the language in a planner. First an intuitive description of what a planner is supposed to do with a DDL.1 specification is given and then a more formal specification of a planning algorithm is presented. To allow comparisons with more conventional planners, we adopt the formal approach currently used in planning literature (e.g., [Weld, 1994]).
The language allows the description of a discrete event dynamic
system, a dynamic system in which state variables may have temporal
evolutions that are piecewise constant functions of time. Such
systems are studied in a sub-area of control theory and optimization
(see for example [Ramadge & Wohnam, 1989]). Here we consider as a temporal
planning problem the problem of deciding an evolution of such systems.
While classical plan-space search planners built a partial plan that
necessarily asserts a conjunction of predicates (goals) in any
possible completion, here a planner searches in the state
variable temporal evolution space to determine those evolutions
that necessarily include certain piece of evolution given as goals.
In other words, planning is this framework consists of determining
the elements of a matrix 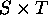 where S is the space of
the state variables and T is the time line.
Some of the values (with a temporal duration) are given as goals and
the planner should find a "convenient position" on the matrix for
those values and fill the rest of the matrix with values compatible
with the goal positioning (i.e., any positioned value should satisfy
all the constraints specified in the DDL.1 domain definition). This
view of planning was first used in HSTS [Muscettola et al., 1992,Muscettola, 1994].
where S is the space of
the state variables and T is the time line.
Some of the values (with a temporal duration) are given as goals and
the planner should find a "convenient position" on the matrix for
those values and fill the rest of the matrix with values compatible
with the goal positioning (i.e., any positioned value should satisfy
all the constraints specified in the DDL.1 domain definition). This
view of planning was first used in HSTS [Muscettola et al., 1992,Muscettola, 1994].
The rest of this Section describes a planning algorithm, named TP-SV (Temporal Planner with State Variables) which works in the framework sketched above.
A TP-SV goal is a 3-ple 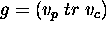 where
where
 and
and  are values of the kind
are values of the kind 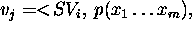
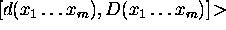 . Both
. Both 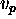 and
and 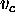 may be either ground or
unground. The tr is either one of the temporal constraints or
nil representing a null constraint:
may be either ground or
unground. The tr is either one of the temporal constraints or
nil representing a null constraint:
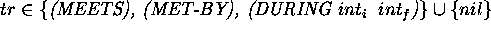
A user goal may be described as the 3-ple: 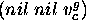 where
where 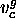 is a completely ground value.
is a completely ground value.
The goal definition allows to represent as planner's goal all the
constraints that should be implemented in the solution. Both the
external goals defined by the user and the domain goal generated by
the compatibility specification are represented with a 3-ple.
The value 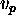 is intended to be a value existing yet in the
current solution which produces (the subscript p stands for
producer) a constraint that requires a new value
is intended to be a value existing yet in the
current solution which produces (the subscript p stands for
producer) a constraint that requires a new value 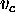 (
c stands for consumer) according to the temporal relation
tr. At present users goals are ground pieces of evolution
independent from each other, this is represented by the nil
``producer'' and the nil ``temporal constraint''.
(
c stands for consumer) according to the temporal relation
tr. At present users goals are ground pieces of evolution
independent from each other, this is represented by the nil
``producer'' and the nil ``temporal constraint''.
A plan in TP-SV is a 4-ple 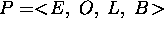 where:
where:
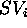
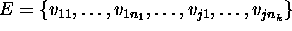
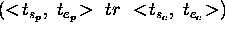 . Where tr represents the
temporal relation among the values
. Where tr represents the
temporal relation among the values 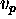 e
e 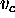 , and the couple
of temporal variables
, and the couple
of temporal variables 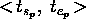 (
(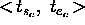 ) represents the start-time and end-time
of the duration interval associated to
) represents the start-time and end-time
of the duration interval associated to 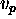 (
(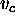 ).
).
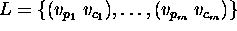 stores the causal relations among elements of E (the
set of causal links). Two elements
stores the causal relations among elements of E (the
set of causal links). Two elements 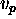 and
and 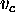 are
each other related by a causal link if the insertion of the element
are
each other related by a causal link if the insertion of the element
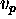 in the domain directly caused the insertion of the element
in the domain directly caused the insertion of the element
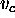 in order to satisfy a compatibility constraint (a goal).
in order to satisfy a compatibility constraint (a goal).
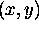 meaning that variables x is substituted with
term y.
meaning that variables x is substituted with
term y.
The planning algorithm TP-SV is shown in Figure 2. The
algorithm builds a ground evolution of the domain by incrementally
posting goals (constraints) on a partial solution.
TP-SV has three input parameters: a plan P,
the list of goals to be achieved, and the domain theory
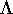 of DDL.1 constraints specification.
of DDL.1 constraints specification.
The planner is given a set of user's goals and starts working on an
empty plan 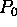 in which any state variable
in which any state variable 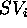 is set to a
steady rest evolution represented with the sequence of values
(
is set to a
steady rest evolution represented with the sequence of values
(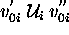 ). The value
). The value 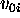 is a
rest value that should be defined for any state-variable. The value
is a
rest value that should be defined for any state-variable. The value
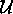 (undefined) initially represents the stretch of temporal
evolution that the planner should define to satisfy goals. A plan is
seen as a sequence of value transitions that starts from some rest
values, evolves to satisfy some goals and return to the rest values.
(undefined) initially represents the stretch of temporal
evolution that the planner should define to satisfy goals. A plan is
seen as a sequence of value transitions that starts from some rest
values, evolves to satisfy some goals and return to the rest values.
More formally the empty plan 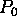 is a 4-ple
is a 4-ple 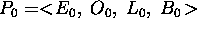 :
:
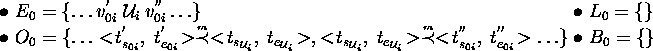
The symbol  stands for MEETS.
stands for MEETS.
Some further observation are worth doing to understand the algorithm
in Figure 2: (a) the planner uses the non-deterministic
operator choose to start separate computations in choice
points; (b) to perform Step 3.a of the algorithm the value 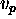 and the tr contained in the goal are used to filter the possible
positions to actually implement the constraint; (c) at Step 5 and 6
the MGU operator computes the Most General Unifier among its
parameters.
and the tr contained in the goal are used to filter the possible
positions to actually implement the constraint; (c) at Step 5 and 6
the MGU operator computes the Most General Unifier among its
parameters.

Figure 2: The basic TP-SV algorithm for DDL.1
The representation language described here has a number of connections with current research. Similar attempts are performed by different people with different points of view but with a common goal of associating ``good theories'' to realistic planning problems.
Extension to classical planning from the formal side. Extension to the STRIPS approaches have been continuously investigated: e.g., Allen's and his students' work on dealing with temporal models of the external world [Allen, 1991], Pednault's proposal for dealing with context dependent effects [Pednault, 1989], recent work by Penberthy's [Penberthy & Weld, 1994] for building up a UCPOP-like planner that uses explicit time, and models changes in the physical world. Our work shares some of these objectives (the representation of time, the representation of dynamic processes) but adopts a different planning perspective using an implicit representation of actions. The emphasis is here on a pragmatically oriented modeling of the world.
Improvements to application-oriented architectures. At least two recent works contain attempts similar to ours to describe more complex domain constraints: (a) the EXCALIBUR planner [Drabble, 1993] uses a qualitative process simulator at execution time to better choose repair strategies; (b) Tate's <I-N-OVA> formalism [Tate, 1995] sees the whole planning process in O-PLAN as the management of various set of constraints.
Planning and Control. The similarity between planning and
control problems was remarked in [Passino & Antsaklis, 1989] and deepened in
[Dean & Wellman, 1991]. Different uses have been done of this similarity:
(a) to investigate planning with uncertainty within a solid formal
framework [Dean & Wellman, 1991]; (b) to consider particular domains in which
tractability results are possible as Bäckström did with the
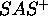 formalism [Bäckström, 1992]. The representation language we
are studying is different from
formalism [Bäckström, 1992]. The representation language we
are studying is different from 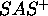 , in particular an explicit
representation of time constraints is here a basic feature. Our aim
is somewhat similar to Dean's but we restrict our analysis to
deterministic discrete event systems.
, in particular an explicit
representation of time constraints is here a basic feature. Our aim
is somewhat similar to Dean's but we restrict our analysis to
deterministic discrete event systems.
Other unconventional approaches. Maybe the more similar approach is Lansky's attempt to see planning as reasoning about events, instead of reasoning about actions [Lansky, 1987]. Starting from that formalism Lansky investigates the use of locality while planning. The problem of decomposing the domain to speed up the resolution process was also one of the main inspirations of the HSTS architecture in its space probe application [Muscettola, 1994].
Knowledge acquisition for planning. As stated in the introduction several studies have recently concerned KA aspects and planning systems. Some work, not strictly related to ours, is devoted to the development of generic models of planning activity (e.g., [Valente, 1995]). Other works are more connected to the DDL.1 effort because it concerns the definition and manipulation of planning knowledge-bases. In [Chien, 1996] a set of tools, in particular static and completion analyzers, is described that support a rule-based planning language definition and maintenance. [desJardins, 1996] is an example of application of learning technique to the refinement of a knowledge-base written in a classical formalism. Close to ours is the work of [Biundo & Stephan, 1996] that presents an approach to the modular and incremental definition of domain descriptions written in a formal language based on temporal logic.
This paper has formally introduced a language for the description of domain planning knowledge. The language is used to specify the relevant constraints in a planning knowledge base. In the paper after a BNF specification of the syntax, a model theoretic semantics for DDL.1 is introduced. Furthermore a planning algorithm is described that uses the features of the language.
Let us now consider again some of the requirements mentioned in the introduction and summarize how they are addressed in DDL.1.
The formal analysis presented in the paper is a starting point for the
creation of a set of tools helping the user in the definition or
revision of a knowledge base. For example, as observed in Section 4,
for a given specification it is possible that 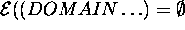 . This means that it is possible to check
whether a given domain specification is inconsistent. It should be
also useful to investigate the possibility for the automatic checking
of such a property.
. This means that it is possible to check
whether a given domain specification is inconsistent. It should be
also useful to investigate the possibility for the automatic checking
of such a property.
Finally, it is worth remembering that the language is a restricted version of
HSTS-DDL which has been used in relevant practical applications both
in space probes activities management and in the description of
complex transportation scheduling problems ---see [Muscettola et al., 1992,Muscettola, 1994].
Although preliminary our work is meant to fill the gap between formal and applicative work in planning and scheduling research. Our contribution to the debate related to KA techniques and planning systems stands in the definition of a language that is centered on the idea that a relevant part of planning knowledge is played by the domain constraints. In our view the elicitation of such constraints is a major point in acquiring knowledge for planning systems, the other point being the extraction of domain heuristics to guide search during problem solving.
This research is partially supported by: ASI - Italian Space Agency, Esprit III BRWG project No.8319 "ModelAge", CNR Committee 04 on Biology and Medicine.
A Representation Language for Domain Knowledge in Planning Architectures
This document was generated using the LaTeX2HTML translator Version 95.1 (Fri Jan 20 1995) Copyright © 1993, 1994, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 0 kaw-96.tex.
The translation was initiated by Vittorio Giannini on Thu Oct 10 16:49:52 MET DST 1996