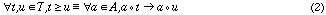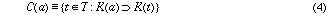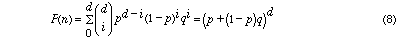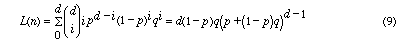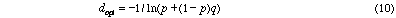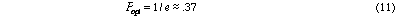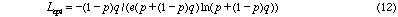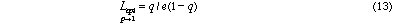Brian R. Gaines
Knowledge Science
Institute
University of Calgary
Alberta, Canada T2N
1N4
gaines@cpsc.ucalgary.ca
http://ksi.cpsc.ucalgary.ca/KSI/
A model is developed of the emergence of the knowledge level in a society of agents where agents model and manage other agents as resources, and manage the learning of other agents to develop such resources. It is argued that any persistent system that actively creates the conditions for its persistence is appropriately modeled in terms of the rational teleological models that Newell defines as characterizing the knowledge level. The need to distribute tasks in agent societies motivates such modeling, and it is shown that if there is a rich order relationship of difficulty on tasks that is reasonably independent of agents then it is efficient to model agents competencies in terms of their possessing knowledge. It is shown that a simple training strategy of keeping an agent's performance constant by allocating tasks of increasing difficulty as an agent adapts optimizes the rate of learning and linearizes the otherwise sigmoidal learning curves. It is suggested that this provides a basis for assigning a granularity to knowledge that enables learning processes to be managed simply and efficiently.
In his seminal paper on the knowledge level Newell (1982) situates knowledge in the epistemological processes of an observer attempting to model the behavior of another agent:
"The observer treats the agent as a system at the knowledge level, i.e. ascribes knowledge and goals to it." (p.106)
emphasizing that:
"The knowledge level permits predicting and understanding behavior without having an operational model of the processing that is actually being done by the agent." (p.108)
He defines knowledge as:
"Whatever can be ascribed to an agent such that its behavior can be computed according to the principle of rationality." (p.105)
noting that:
"Knowledge is that which makes the principle of rationality work as a law of behavior." (p.125)
and defining rationality in terms of the principle that:
"If an agent has knowledge that one of its actions will lead to one of its goals, then the agent will select that action." (p.102)
Newell's argument form is a cybernetic one of the type originated by Wiener (1948) and refined by Ashby (1956) whereby an arbitrary system is treated as a black box to be modeled on the basis of its input/output behavior with no presuppositions about its internal structure. Ashby (1952) used this argument form to derive many phenomena of living systems, such as habituation, from general properties, such as the existence of many alternative attractors in the state system. Zadeh (1964) developed the abstract formulation of system identification from a cybernetic stance, showing how the notion of state is an abstraction introduced in modeling formalisms to account for the influence of past experience on future behavior. Gaines (1977) developed general algorithms for such identification in terms of arbitrary measures of model complexity and of the approximation of a model to observed behavior, and showed that appropriate measures led to optimal identification of deterministic and stochastic automata from their behavior. He emphasizes the formal arbitrariness of the presuppositions underlying a modeling schema, and shows that inappropriate presuppositions lead to indefinitely complex models (Gaines, 1976).
In the light of these analyses, Newell's arguments may be seen as stating that knowledge is a state variable imputed by a modeler in order to account for its behavior, and that the appropriate presuppositions for modeling an agent are those of rational teleology, that it has goals and acts to achieve them. Two fundamental questions arise about Newell's framework for knowledge, one reaching backwards to the justification of modeling behavior teleologically in terms of goals and their rational achievement, and the other reaching forwards to the nature of the knowledge state space that an observer will generate, its detailed qualitative and quantitative characteristics.
The next section briefly examines the preconditions for rational teleological models to be effective, and the remainder of the paper develops in depth the structure of knowledge models that will arise in a society of agents.
One way of analyzing the foundations of rational teleological models is to assume that they have none--that the modeling of other agents in terms of goals and knowledge is justified to the extent that it works--a pragmatic argument of the form developed by Peirce and James (Ayer, 1968). This assumption is that of Dennett's (1987) intentional stance, and it is in accordance with the basic theory of modeling, the Popperian position that our presuppositions in modeling are but conjectures subject to refutation if we are not satisfied with the results of using them (Popper, 1963). Modeling theory tells us that if the intentional stance was not appropriate to modeling human agents then it would lead to complex models with poor predictive power and we would find it more useful to adopt some other stance.
However, it is useful to examine some simple systemic characteristics of agents that would justify the use of rational teleological models if only to illustrate how few presuppositions are necessary for the model to be useful (Gaines, 1994). The most fundamental properties which we impute to any system are its existence and persistence over time. A system is identifiable as not having existed before some time, of definitely existing after some later time, of persisting in existence until some later time, and of not existing again after some later time. This coming into existence, persisting for while, and going out of existence again is a common property of all systems. It applies to both living and non-living systems, and in living systems it applies at all levels from cell to species.
What characterizes living systems are the recursive activities of self-replication underlying their persistence, that they actively and continually create the conditions for their persistence. Maturana (1975) has proposed that this is the fundamental distinction between living and non-living systems. Autopoietic systems:
"are systems that are defined as unities as networks of production of components that (1) recursively, through their interactions, generate and realize the network that produces them; and (2) constitute in the space in which they exist, the boundaries of this network as components that participate in the realization of the network...a living system is an autopoietic system in physical space." (Maturana, 1981)
However, there is no notion of goals or knowledge in Maturana's definition, and no ascription of intentions to living systems. A reactive persistent system in itself has no goals or intentions. It reacts to its environment through mechanisms that tend to maintain its persistence despite changes in its environment. An external observer may model this behavior as goal-directed because that provides a simple predictive explanation. That is, if an autopoietic system when disturbed, regardless of what state it is triggered into, seems to return to its original state, it is naturally modeled as goal-seeking. If the system's environment happens to contain other systems like itself and the system's activities include observation and modeling, it may model the other systems as goal-directed, and then by analogy come to model itself as goal-directed. This is a natural outcome of autopoiesis in a social environment.
As well as not reading too much into models of autopoietic systems, it is important to note that we can ascribe very little to their existence. A chaotic universe has a probability of producing any system including autopoietic systems. Once such systems exist and are modeled properties emerge (Sharif, 1978). As Peirce remarks:
"Law begets law; and chance begets chance...the first germ of law was an entity which itself arose by chance, that is as a First." (Peirce, 1898)
Jantsch (1980) and Prigogine (1984) have developed detailed models of how organization emerges from chaos. Gould (1989) has analyzed the fossil record and modeled the genesis and extinction of a wide variety of species as low probability random events. Monod (1972) has given a biochemical model of life as an improbable phenomena that, once it exists, follows deterministic laws. When a living system comes into existence it acts to persist, but, from the systemic perspective advanced by Maturana, this is the definitional property by which we recognize its existence as a living system, not an additional property going beyond active persistence.
Barrow and Tipler (1986) have analyzed the remarkably narrow physical conditions under which life as we know it can exist, and when one examines the mechanisms by which a living organism narrows these conditions even further in order to persist it is natural to ascribe purpose to its activity. For example, Cannon (1932), terms such activity homeostasis and part of The Wisdom of the Body and Ashby (1952) in analyzing homeostasis as part of his Design for a Brain models it as a goal-directed process. However, he also shows how such apparently goal-directed behavior arises in any system with many states of equilibrium. The utility of an intentional stance stems from simple systemic considerations, and one has to be careful in reifying the notion of agency to realize that the additional assumption of the existence of some reified `agent' is also a matter of utility, not of existential proof or necessity.
In Ashby's day a system that reacted to its environment by acting until it arrived in a new mode of equilibrium would be seen as not only counter-acting the effects of the environment but also arriving at some state that was determined by those effects, that is, apparently targeted upon them. Nowadays, with the realization that strange attractors are prevalent in all forms of physical system (Ruelle, 1989), and particularly in biological processes and their higher-order manifestations such as brains (Basar, 1990), societies (Dendrinos and Sonis, 1990) and cultural phenomena (Hayles, 1991), it would be realized that the final state may be one of very many that have the equilibrating effect but is neither determined by the effects of the environment nor targeted upon them.
In particular, the definition of fitness of a species in evolutionary terms is merely a restatement of the species' persistence in terms of the environment in which it persists. As Ollason argues:
"Biologists use the concept of fitness as the explanation of the truly inexplicable. The process of evolution is exactly what the etymology of the word implies: it is an unfolding, an indeterminate, and in principle, inexplicable unfolding. (Ollason, 1991)
A species is fit to exist in an environment in which it happens to persist. As noted in the previous paragraph, this does not mean it was targeted on that environment or that there is a determinate relation between the nature of the environment and the species that happens to have evolved. The environment acts as a filter of species and those that persist are fit to survive. There are no teleological implications, and this model does not give `survival-directed' behavior any greater probability of leading to persistence than any other behavior. Gould (1989) details the random phenomena that have made particular species fit to persist for a while in the fossil record. Bickerton (1990) argues that there is no evidence for what we deem to be high-level human traits to have survival value--intelligence and language have at least as many disadvantages as advantages, and may be seen as of negative value to the survival of the human species.
Thus, in adopting an intentional stance one is selecting a modeling schema for its simplicity, convenience and utility. Newell's notions of rationality, goals and knowledge have no epistemological content and are circularly derivable from one another as definitions of what it is to adopt an intentional stance. The knowledge level can be reified only through our first being satisfied that it has predictive capabilities, and then through our further presupposing that there must be some real phenomenon out there that makes that prediction possible. We have to be very careful in testing both of these conditions: the reflexivity of social interactions means that changes in our behavior based on assumptions about another's intentions may lead to contingent behavior on the part of the other (Levis, 1977) giving rise to apparent predictive validity; and the predictive capabilities of a cybernetic model of a black box place very few constraints on what structure actually exists within the box.
The previous section having warned against reading too much into knowledge level models, the current one will build such a model based on a sequence of plausible assumptions largely concerned with cognitive ergonomics--of building models that require as little effort to develop as possible. The starting point is Newell's notion that the knowledge level originates in one agent attempting to model another, and hence is essentially a product of a social process. One can ask the question "why should it be valuable to model another agent" and come to the conclusion that the human species is characterized by its social dependencies, the divisions of labor whereby many of the goals of one agent are satisfied through the behaviors of others. In these circumstances one agent will model another in instrumental terms, in terms of its capabilities to carry out tasks that will lead to the modeling agent's goals being satisfied--and, vice versa, the other agent will model the first in a reciprocal fashion.
Consider a set of agents, A, and a set of tasks, T, such that it is possible
to decide for each agent, a
A whether it can carry out a task
tT. Assume, without loss of generality, that this is a binary
decision in that performance at different levels is assumed to define different
tasks, and that we can write
a
t
for the truth value that agent a can carry out task t. We can then characterize
an agent's competence, C(a), by the set of tasks which it can carry out:
If one agent knows C(a) for another agent, a, then it knows its competence in terms of the tasks it can carry out and can plan to manage its goals by allocating appropriate tasks to the other agent.
However, keeping track of the competencies of relevant agents in terms of extensive sets of tasks for which they are competent is inefficient both in knowledge acquisition and storage if there are many dependencies between tasks such that the capability to carry out one task is a good predictor of the capability to carry out another. A partial order of difficulty on tasks, >=, may be defined such that the capability to carry out a task of a given difficulty indicates the capability to carry out tasks of lesser difficulty in the partial order:
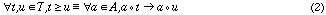
If, there is a rich partial order on tasks independent of agents then it becomes reasonable to attempt to represent the partial order as one embedded in the free lattice generated by some set, K, which we shall term knowledge. Since the free lattice generated by a set of cardinality, n, has 2n distinct members, there is potentially an exponential decrease in the amount of information to acquire and store about an agent if it is characterized in terms of its set of knowledge rather than the set of tasks it can perform. This decrease will be realized to the extent that the embedding of the task dependencies in a free lattice involves tasks corresponding to all elements of the lattice. Thus, we posit a set of knowledge, K, such that a task, t, is characterized by the set of knowledge, K(t), required to carry it out, and the order relation between tasks corresponds to subset inclusion of knowledge:
An agent, a, is characterized by the knowledge it possesses, K(a), and this determines its competence in terms of tasks:
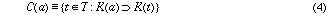
The development to this stage parallels that of knowledge spaces as defined by Falmagne, Koppen, Villano, Doignon and Johannesen (1990), and applied by them to testing a student's knowledge. However, the move from an extensional specification in terms of tasks to an extensional specification in terms of knowledge is inadequate to account for situations where the capability to carry out one task may indicate the capability to carry out an infinite number of lesser tasks. Extensionally, this involves indexing the lesser tasks as involving an infinite set of knowledge, but, as Newell (1982) notes it is better represented by a schema in which knowledge is generated from knowledge.
If x is a subset of knowledge then G(x) may be defined as the subset which can be generated from it subject to the obvious constraints that:-
--the original knowledge is retained:
--all of the knowledge that can be generated is included:
--additional knowledge generates additional knowledge:
Tarski (1930) noted that the consequence operator of any deductive system has these properties, and Wójcicki (1988) has used it conversely to characterize any closure operator satisfying (5) through (6) as a logic. As Rasiowa and Sikorski (1970) remark:
"the consequence operation in a formalized theory T should also be called the logic of T"
that is, every generator defines a formal logic.
The development of this section has arrived at a characterization of the knowledge level that corresponds to the folk psychology notion that agents can be modeled as possessing something termed knowledge, and the cognitive science notion that the capability to generate knowledge from knowledge corresponds to a formal deductive logic. What presuppositions have been involved in this development?
These are strong presuppositions but ones that seem to work reasonably well in characterizing human agents--we are acutely aware of the exceptions and treat them as anomalies.
What the development does not do is characterize the nature of knowledge, other than as an arbitrary index set used in modeling. It would be reasonable to suppose that our actual definitions of knowledge elements would be closely related to our definitions of, and terminology for, tasks--for example, that someone capable of adding numbers might be said to have "knowledge of addition." However, too close a link to tasks would reduce the benefits of representing capabilities through subsets of knowledge rather than subsets of tasks, and hence we would expect an attempt to characterize knowledge in a way that abstracts away from tasks and looks for more general knowledge elements that underlie a range of tasks.
However, P1 above is counter to another major reason why one agent may wish to characterize the capabilities of another. Human agents are not created with innate knowledge but instead learn to undertake an ever increasing set of tasks. Agents expect C(a) to increase with experience and they manage the learning environments of other agents so as to maximize the rate of increase in directions appropriate to the needs of society. Thus, there is another major aspect to the characterization of an agent's knowledge--"how does it relate to the management of their learning--their training and education?"
The following sections develop a theory of the management of learning which gives further insights into the properties of a useful characterization of the knowledge level, particularly the granularity of knowledge.
Early research on learning machines (Gaines and Andreae, 1966) saw these machines as computational modules that could be programmed indirectly through experience, and focused on the manipulation of the modules through coding, priming and training (Gaines, 1968).
Coding is concerned with appropriate input and output interfaces which are known to be critical to the learning capabilities of both machines and people--minor changes in information encoding can change a task from one which is very easy to learn to one which is virtually impossible.
Priming is concerned with the transfer of knowledge not through learning from experience but through other mechanisms such as mimicry, analogy and language (Gaines, 1969). It was shown that mechanisms for the linguistic transfer of control strategies to perceptron controllers could decrease their learning time in a way similar to that for human controllers given the same instructions (Gaines, 1972a), and make the difference between a task being very easy or virtually impossible to learn. These result led to experiments with the use of linguistic fuzzy hedges (Zadeh, 1973) for priming learning machines with the surprising result that priming alone was sufficient to induce excellent performance in some situations (Mamdani and Assilian, 1975), triggering the development of fuzzy control (Sugeno, 1985).
Training is concerned with the sequence of learning environments presented to the learning system in order to maximize its rate of learning. It was shown that for both learning machines and people a `feedback trainer' that adjusted the difficulty of a task to keep performance constant greatly increased the speed of learning, and that tasks which were virtually impossible to learn under conditions of fixed difficulty could be learned rapidly with feedback training (Gaines, 1968; Gaines, 1972b).
The effects of coding, priming and training are basic phenomena in any learning system. Now that the aspirations of the 60s are beginning to be filled by the intelligent adaptive agents of the 90s, it is timely to revisit some of these phenomena. In particular, research in distributed artificial intelligence (Bond and Gasser, 1988), artificial life (Langton, 1995), and cultural evolution (Boyd and Richerson, 1985), raises issues of how a society of agents interacts to provide one another with mutual training environments.
The next section describes a collective stance model of learning phenomena in agent communities that accounts for the development of functional differentiation in uniform populations of adaptive agents. The following section develops a quantitative model of the way in which the sigmoidal learning curves of agents learning in static environments can be linearized through feedback training, and uses this model to account for a range of phenomena in communities of intelligent adaptive agents.
A useful perspective from which to examine learning phenomena in agent societies is a collective stance (Gaines, 1994) in which the society is viewed as a single adaptive agent recursively partitioned in space and time into sub-systems that are similar to the whole. In human terms, these parts include societies, organizations, groups, individuals, roles, and neurological functions (Gaines, 1987). Notions of expertise arise because the society adapts as a whole through the adaption of its individual agents. The phenomena of expertise correspond to those leading to distribution of tasks and functional differentiation of the individual agents.
The mechanism for functional differentiation is one of positive feedback from agents allocating resources for action to other agents on the basis of those latter agents' past performance of similar activities (Gaines, 1988). Distribution and differentiation follow if performance is rewarded, and low performers of tasks, being excluded by the feedback mechanism from opportunities for performance of those tasks, seek out alternative tasks where there is less competition.
The knowledge-level phenomena of expertise, such as meaning and its representation in language and overt knowledge, arise as byproducts of the communication, coordination and modeling processes associated with the basic exchange-theoretic behavioral model. The collective stance model can be used to account for existing analyses of human action and knowledge in biology, psychology, sociology and philosophy (Gaines, 1994).
Simple simulation experiments of a competitive environment for two agents can illustrate the formation of expertise through positive feedback (Gaines, 1988). For example, let the rules of a basic phenomenological simulation be that: each problem requires certain knowledge; if the agent does not have the knowledge necessary it guesses with a probability of success, learning if it succeeds; the society chooses the expert for a problem with equal probability initially, gradually biasing the choice according to success or failure; there is no communication of knowledge between experts. Figure 1 graph A plots the probability that one agent will be always preferred and shows that this rapidly approaches 1.0--a best `expert' is determined. Graph B shows the expected knowledge of the better expert and graph C that of the rival--one goes to 100% rapidly and the other is asymptotic to about 36%--there is objective evidence of the superior ability of the chosen expert. Which of the two agents becomes the `best expert' is, of course, completely chance.
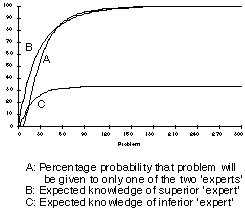
Figure 1 Simulation of the effects of positive feedback on the formation of expertise
The simulation shown is not Monte Carlo but based on the calculation of the exact probability distributions involved. It can easily be adjusted to take into account differences between the experts: that one starts with greater knowledge; that one learns faster; that one is favored initially (the prima facie credibility or `well-dressed consultant' phenomenon). Similar simulations have been made of different positive feedback mechanisms; for example, if both experts are given the same problem but the problem difficulty is adjusted upwards if either gets it right--the situation of keeping up in the scientific `rat race.' Effects have been introduced of the loss of knowledge through inadequate opportunities for its application, the growth of scientific knowledge so that there is always more to be acquired, and differential access to priming through cultural knowledge transfer processes such as education. All the simulations bear out the expected qualitative result, that a range of different positive feedback mechanisms in an agent society are adequate to account for differential expertise in a sample with initially equal knowledge and capabilities.
There is evidence that these processes occur in human communities. Sociologists have noted positive feedback processes in the dynamics of the scientific community (Hagstrom 1965). Merton (1973) coined the term the "Matthew effect" for those features of the reward system in research that were biased towards allocating greater credit for the same discovery to those with an already established reputation. In medicine, a key learning resource is access to medical problems, and the `owner' of such a problem has a keen personal interest in only allowing someone of very good reputation to handle it. The system, including considerations of legal liability, funnels problems to those who are regarded as experts. It is, however, precisely these problems from which new knowledge is generated. Similar considerations apply to the award of scholarships, invitations to scientific congresses, and so on (Blume 1974). They also apply not only to individuals but also to social units such as a company subject to government procurement procedures that are heavily biased to contractors with `prior experience' and with whom the government agency has `prior experience.'
The effect upon individual agents of the social feedback processes described in the previous section is to regulate the learning experiences available to the agent in such a way that agents with historically better performance get the tasks judged to be more difficult. In a world with a wide range of tasks of varying difficulty and with agents having limited capacities and lives, the overall effect is that each agent's performance is kept roughly constant as it is given tasks of increasing difficulty commensurate with its learning as indicated by its performance on previous tasks. The agent is learning to cope with tasks of increasing difficulty so that its skills are increasing, but being constantly presented with tasks just beyond its capabilities so that its performance is not.
It is interesting to attempt to develop a qualitative model of the learning phenomena involved using as weak assumptions about the adaptive agent as possible so that the model is widely applicable. Consider again the universe of tasks and a universe of knowledge such that an agent can perform a task if it has some, not necessarily unique, collection of knowledge. Assume that the difficulty of a task can be estimated in terms of the cardinality of a set of knowledge that allows an agent to perform it. Assume that when an agent is given a task for which its knowledge is inadequate that the probability of it guessing each missing item of knowledge is q and that if it guesses all the missing items it performs the task and learns the knowledge, but otherwise learns nothing.
Assume that the training system can select a task at a given level of difficulty but does not know either the knowledge required to perform it or the state of the agent's knowledge.
Assume that the probability that the agent knows a randomly selected item of knowledge is p, and that the probability that it learns an unknown item during a task necessitating it is q.
Then the probability that an agent will perform a task of difficulty d is:
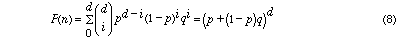
and the expected rate of learning is:
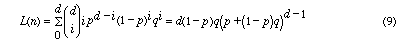
If one selects a task difficulty that optimizes the rate of learning by maximizing L(n) with respect to n then:
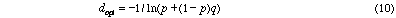
and the expected performance to achieve this is:
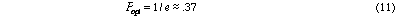
and the expected maximum rate of learning is:
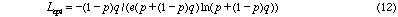
which is such that as agent learns and p approaches 1:
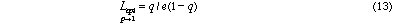
The implication of equation (11) is highly significant because it implies that a training system that adjusts the task difficulty to keep performance constant will achieve a linear rate of learning that is the fastest possible.
One can also deduce from equation (11) that the optimum performance involves the learning agent being correct 37% of the time--i.e. an error rate of 63%. However, this result is misleading unless one does a sensitivity analysis. Such an analysis shows that the learning rate drops to half optimum when the error rate decreases to 20% or increases to 80%--i.e. that the optimum learning performance is relatively insensitive to the performance set-point chosen. The reason for this is that there is a lower chance of learning more with tasks of higher difficulty, and a greater chance of learning less with tasks of lower difficulty.
Thus a feedback trainer that adjusts task difficulty to maintain performance constant can induce optimum learning in an adaptive agent, and achieve something close to this even if the performance fluctuates over a 5 to 1 range.
What happens if an adaptive agent is given tasks to perform of constant difficulty. One would expect the learning rate to be sub-optimal initially because the task is to difficult, become optimal for a period as the performance improves to a level where the difficulty is optimal, then decline again as the performance improves to a level where the task is too easy. Figure 2 shows this results of integrating equation (9) for fixed n compared with the results of integrating (12), with q = 0.5 and full knowledge being 25 items. It can be seen that feedback training achieves a speedup in learning by a factor of 2 compared with the best fixed-difficulty training, that the learning curves have the expected sigmoidal shape, and that training on tasks of high difficulty involves very long learning periods.
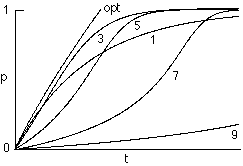
Figure 2 Learning curves for adaptive agent under various training conditions
In practice there may be complications that make the effects shown even more pronounced. For example, the universe of simple tasks may be incomplete in that some knowledge items may only be brought into use in relation to more complex tasks. Such dependencies between knowledge items make feedback training essential.
Returning to the model of the knowledge level developed in Section 3, it is reasonable to hypothesize that if our knowledge level models are effective in terms of training, such that optimum training leads to linear increase in knowledge with time then the natural units of knowledge are those of improvements per unit time in adaptive behavior. That is, the granularity of knowledge should tend to be such that the feedback training strategy is effective in linearizing the learning curve. This is the transition that society undergoes in new areas of knowledge between the era of the "inventor" when the learning curves are long and sigmoidal, to the era of the "textbook" when learning curves are comparatively short and linear. The transition is one of developing knowledge structures that make learning manageable.
This article has emphasized the social provision of the optimal training conditions for learning. However, what motivates the learner to seek out these conditions? Csikszentmihalyi's (1990) concept of flow as the phenomenon underlying the psychology of optimal experience provides a model of the learner dynamics. Hoffman and Novak (1995) summarize the concept as:-
"Flow has been described as `the process of optimal experience' achieved when a sufficiently motivated user perceives a balance between his or her skills and the challenges of the interaction, together with focused attention."
The likeability of a task correlates with a flow state in which a motivated user undertakes a task whose level of difficulty is at some particular level that suits their individual needs. Too low a level results in boredom and too high a level in anxiety, and the optimal level results in the intense satisfaction with the activity that Csikszentmihalyi terms flow.
As the agent learns a flow state can be maintained only by increasing the task difficulty to keep the performance constant. As shown in Section 6, this also maximizes the rate of learning, and this suggests that the flow process may have evolved phylogenetically as a mechanism reinforcing an agent which is maximizing its rate of learning. If the reinforcement center in the brain is stimulated by conditions that optimize learning, then individuals will be attracted to socially created learning environments.
In a society of agents the knowledge processes of an individual agent can become critically dependent on knowledge processes in the society as a whole. It is useful to adopt a collective stance that views the overall society as a larger adaptive agent that is recursively divided into adaptive sub-agents. The resources for an agent include other agents, and some of an agent's processes will be devoted to modeling other agents' capabilities and others to developing those capabilities.
This article has developed a model for the knowledge level based upon the notion that knowledge is a state variable imputed by one agent to another in modeling its capabilities to carry out tasks. This is a cognitively efficient model if there is a rich order relationship of difficulty on tasks that is reasonably independent of agents and enables competence on one task to be predicted from that on others.
It has described a model for adaptive interactions in societies of adaptive agents in which knowledge arises as a state variable imputed by one agent to another to account for its capabilities, and task allocation between agents results in functional differentiation in an initially homogeneous society.
It has been shown that a simple training strategy of keeping an agent's performance constant by allocating tasks of increasing difficulty as an agent adapts optimizes the rate of learning and linearizes the otherwise sigmoidal learning curves.
It has been suggested that this is the basis for the human preference for a flow condition in which the challenge of a task is managed to remain between the extremes of boredom and anxiety. In conclusion, it is suggested that the approach taken in this paper provides the foundations for a bridge between cybernetic, phenomenological models of adaptive interactions in societies of agents and knowledge-level modeling of the same phenomena. The simple model of knowledge as a state variable imputed by one agent in modeling another is sufficient to account for the performance-based training phenomena described. However, such training is powerful precisely because it is independent of exact knowledge of that state variable. If some knowledge is available then tasks may be selected that are specific to the state of knowledge of the trainee. Other knowledge transfer phenomena such as mimicry and language may also be modeled and controlled in similar terms. The higher-level knowledge processes in societies of adaptive agent may be modeled as natural extensions of the basic phenomena described.
Financial assistance for this work has been made available by the Natural Sciences and Engineering Research Council of Canada.
Ashby, W.R. (1952). Design for a Brain. London, UK, Chapman & Hall.
Ashby, W.R. (1956). An Introduction to Cybernetics. London, UK, Chapman & Hall.
Ayer, A.J. (1968). The Origins of Pragmatism. London, MacMillan.
Barrow, J.D. and Tipler, F.J. (1986). The Anthropic Cosmological Principle. Oxford, Clarendon Press.
Basar, E., Ed. (1990). Chaos in Brain Function. Berlin, Springer.
Bickerton, D. (1990). Language and Species. Chicago, University of Chicago Press.
Bond, A.H. and Gasser, L., Ed. (1988). Distributed Artificial Intelligence. San Mateo, Morgan Kaufmann.
Boyd, R. and Richerson, P.J. (1985). Culture and the Evolutionary Process. Chicago, Illinois, University of Chicago Press.
Cannon, W.B. (1932). The Wisdom of the Body. London,
Csikszentmihalyi, M. (1990). Flow: The Psychology of Optimal Experience. New York, Harper and Row.
Dendrinos, D.S. and Sonis, M. (1990). Chaos and Socio-Spatial Dynamics. Berlin, Springer.
Dennett, D.C. (1987). The Intentional Stance. MIT Press, Cambridge, Massachusetts.
Falmagne, J.-C., Koppen, M., Villano, M., Doignon, J.-P. and Johannesen, L. (1990). Introduction to knowledge spaces: how to build, test and search them. Psychological Review 97(2) 201-224.
Gaines, B.R. (1968). Training the human adaptive controller. Proceedings of the Institution of Electrical Engineers 115(8) 1183-1189.
Gaines, B.R. (1969). Adaptively controlled instruction for a tracking skill. Programmed Learning Research. Sciences de Comportement. pp.321-336. Paris, Dunod.
Gaines, B.R. (1972a). The learning of perceptual-motor skills by men and machines and its relationship to training. Instructional Science 1(3) 263-312.
Gaines, B.R. (1972b). Training, stability and control. Instructional Science 3(2) 151-176.
Gaines, B.R. (1976). On the complexity of causal models. IEEE Transactions on Systems, Man & Cybernetics SMC-6(1) 56-59.
Gaines, B.R. (1977). System identification, approximation and complexity. International Journal of General Systems 2(3) 241-258.
Gaines, B.R. (1987). Positive feedback processes underlying functional differentiation. Caudhill, M. and Butler, C., Ed. Proceedings of IEEE First International Conference on Neural Networks. Vol.2. pp.387-394.
Gaines, B.R. (1988). Positive feedback processes underlying the formation of expertise. IEEE Transactions on Systems, Man & Cybernetics SMC-18(6) 1016-1020.
Gaines, B.R. (1994). The collective stance in modeling expertise in individuals and organizations. International Journal of Expert Systems 7(1) 21-51.
Gaines, B.R. and Andreae, J.H. (1966). A learning machine in the context of the general control problem. Proceedings of the 3rd Congress of the International Federation for Automatic Control. London, Butterworths.
Gould, S.J. (1989). Wonderful Life: The Burgess Shale and the Nature of History. New York, Norton.
Hayles, N.K., Ed. (1991). Chaos and Order: Complex Dyanmics in Literature and Science. Chicago, University of Chicago Press.
Hoffman, D.L. and Novak, T.P. (1995). Marketing in Hypermedia Computer-Mediated Environments: Conceptual Foundations. Owen Graduate School of Management, Vanderbilt University, Nashville, TN. http://www2000.ogsm.vanderbilt.edu/cmepaper.revision.july11.1995/cmepaper.html.
Jantsch, E. (1980). The Self-Organizing Universe. Oxford, Pergamon Press.
Langton, C.E., Ed. (1995). Artificial Life: An Overview. Cambridge, Massachusetts, MIT Press.
Levis, A.J. (1977). The formal theory of behavior. Journal of Social Psychiatry 23(2)
Mamdani, E.H. and Assilian, S. (1975). An experiment in linguistic synthesis with a fuzzy logic controller. International Journal Man-Machine Studies 7(1) 1-13.
Maturana, H.R. (1975). The organization of the living: A theory of the living organization. International Journal Man-Machine Studies 7(3) 313-332.
Maturana, H.R. (1981). Autopoiesis. Zeleny, M., Ed. Autopoiesis: A Theory of Living Organization. pp.21-33. North Holland, New York.
Monod, J (1972). Chance and Necessity. London, Collins.
Newell, A. (1982). The knowledge Level. Artificial Intelligence 18(1) 87-127.
Ollason, J.G. (1991). What is this stuff called fitness? Biology and Philosophy 6(1) 81-92.
Peirce, C.S. (1898). Reasoning and the Logic of Things. Cambridge, Massachusetts, Harvard University Press.
Popper, K.R. (1963). Conjectures and Refutations: The Growth of Scientific Knowledge. London, Routledge & Kegan Paul.
Prigogine, I. (1984). Order out of Chaos. Toronto, Bantam.
Rasiowa, H. and Sikorski, R. (1970). The Mathematics of Metamathematics. Warsaw, PWN.
Ruelle, D (1989). Chaotic Evolution and Strange Attractors. Cambridge, UK, Cambridge University Press.
Sharif, N. (1978). An introduction to modeling. Sharif, N. and Adulbhan, P., Ed. Systems Modeling for Decision Making. pp.1-21. Bangkok, Asian Institute of Technology (distributed by Pergamon Press).
Sugeno, M. (1985). Industrial Applications of Fuzzy Control. Amsterdam, North-Holland.
Tarski, A. (1930). Fundamentale Begriffe der Methodologie der deduktiven Wissenschaften I. Monatahefte für Mathematik und Physik 37 361-404.
Wiener, N. (1948). Cybernetics or Control and Communication in Animal and Machine. Cambridge, Massachusetts, MIT Press.
Wójcicki, R. (1988). Theory of Logical Calculi. Dordrecht, Kluwer.
Zadeh, L.A. (1964). The concept of state in system theory. Mesarovic, M.D., Ed. Views on General Systems Theory: Proceedings of the Second Systems Symposium at Case Institute of Technology. New York, John Wiley.
Zadeh, L.A. (1973). Outline of a new approach to the analysis of complex systems and decision processes. IEEE Transactions on Systems, Man and Cybernetics SMC-3 28-44.