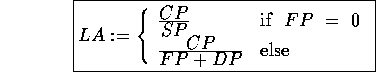Automated Knowledge Acquisition Meets Metareasoning:
Incremental Quality Assessment of Concept Hypotheses during Text
Understanding
Udo Hahn, Manfred Klenner & Klemens Schnattinger
Computational Linguistics Lab -- Text Knowledge Engineering Group
Freiburg University
Platz der Alten Synagoge 1, D-79085 Freiburg, Germany
{hahn,klenner,schnattinger}@coling.uni-freiburg.de
Abstract:
We introduce a methodology for automated knowledge acquisition and
learning from texts that relies upon
a quality-based model of terminological reasoning.
Concept hypotheses
which have been derived in the course of the text understanding process
are assigned specific "quality labels" (indicating their
significance, reliability, strength).
Quality assessment of these hypotheses accounts for
conceptual criteria referring to their current knowledge base context
as well as linguistic indicators (grammatical constructions, discourse patterns),
which led to their generation.
We advocate a metareasoning approach which allows for the
quality-based evaluation and a bootstrapping-style selection of
alternative concept hypotheses as text understanding incrementally
proceeds. We also provide a preliminary empirical evaluation,
with focus on the learning rates and the learning accuracy that
were achieved using this approach.
INTRODUCTION
The work reported in this paper is part of a large-scale project
aiming at the development of
a German-language text knowledge acquisition system [Hahn et al.1996c]
for two real-world application domains --
test reports on information technology products
(current corpus size: approximately 100 documents with 105 words)
and medical findings reports
(current corpus size: approximately 120,000 documents with 107 words).
The knowledge acquisition problem we face is two-fold.
In the information technology domain
lexical growth occurs at dramatic rates -- new products, technologies,
companies and people continuously enter the scene such that any attempt
at keeping track of these lexical innovations by hand-coding is clearly
precluded.
Compared with these dynamics, the medical domain is
lexically more stable but the
sheer size of its sublanguage (conservative estimates range
about 106 lexical items/concepts) also
cannot reasonably be coded
by humans in advance.
Therefore, the designers of text understanding systems
for such challenging applications have to find ways
to automate the lexical/concept learning phase as a prerequisite
and, at the same time, as a constituent part
of the text knowledge acquisition process.
Unlike the current mainstream with its focus on statistically based learning
methodologies [Lewis1991,Resnik1992,Sekine et al.1992],
we advocate a symbolically
rooted approach in order to break the concept acquisition
bottleneck. This approach is based on expressively rich
knowledge representation models of the underlying domain
[Hahn et al.1996a,Hahn et al.1996b,Hastings1996].
We consider the problem of natural language based knowledge acquisition
and concept learning from a new methodological perspective,
viz. one based on metareasoning about statements expressed in
a terminological knowledge representation language.
Reasoning either is about structural linguistic properties
of phrasal patterns or discourse contexts in which unknown words occur
(assuming that the type of grammatical construction exercises
a particular interpretative force on the unknown lexical item),
or it is about conceptual properties of particular concept hypotheses
as they are generated and continuously refined by the on-going
text understanding process (e.g., consistency relative to already
given knowledge, independent justification from several sources).
Each of these grammatical, discourse or conceptual indicators is assigned
a particular "quality" label.
The application of quality macro operators,
taken from a "qualification calculus" [Schnattinger &
Hahn1996],
to these atomic quality labels finally
determines, which out of several alternative hypotheses actually hold(s).
The decision for a metareasoning approach
is motivated by requirements which
emerged from our work in the overlapping fields of natural
language parsing and learning from texts.
Both tasks are characterized by the common need to evaluate
alternative representation structures, either reflecting parsing
ambiguities
or multiple concept hypotheses.
For instance, in the course of concept learning from texts,
various and often conflicting concept hypotheses for a single item are formed
as the learning environment usually provides only inconclusive evidence for
exactly determining the properties of the concept to be learned.
Moreover, in "realistic" natural language understanding systems
working with large text corpora,
the underdetermination of results
can often not only be attributed to incomplete knowledge provided
for that concept in the data (source texts),
but it may also be due to imperfect
parsing results (originating from lacking lexical, grammatical,
conceptual specifications, or ungrammatical input).
Therefore, competing hypotheses at different levels of validity and reliability
are the rule rather than the exception and, thus, require appropriate
formal treatment.
Accordingly, we view the problem of choosing from among several alternatives
as a quality-based decision task which can be decomposed into three
constituent parts: the continuous generation of quality labels for
single hypotheses (reflecting the reasons for their formation
and their significance in the light of other hypotheses),
the estimation of the overall credibility of single hypotheses
(taking the available set of quality labels for each hypothesis into
account), and the computation of a preference order for the
entire set of competing hypotheses, which is based on these
accumulated quality judgments.
ARCHITECTURE FOR QUALITY-BASED KNOWLEDGE ACQUISITION
The knowledge acquisition methodology
we propose is heavily based on the representation
and reasoning facilities provided by terminological knowledge
representation languages (for a survey, cf. woods92).
As the representation of alternative hypotheses
and their subsequent evaluation turn out to be major requirements of
that approach, provisions have to be made to reflect these design
decisions by an appropriate system architecture of the knowledge
acquisition device (cf. Fig.1). In
particular,
mechanisms should be provided for:
- Expressing quality-based assertions about propositions in a
terminological language; these metastatements capture the
ascription of belief to these propositions, the reasons why they came
into existence, the support/weakening they may have received from
other propositions, etc.
- Metareasoning in a terminological knowledge base about
characteristic properties and relations between certain propositions;
the corresponding second-order expressions refer to
propositions (ABox elements)
as well as concept and role definitions (TBox elements).
The notion of context we use as a formal foundation for terminological
metaknowledge and metareasoning is based on McCarthy's context model
[McCarthy1993]. We here distinguish two types
of contexts,
viz. the initial context and the metacontext.
The initial context contains the
original terminological knowledge base (KB kernel) and
the text knowledge base, a representation layer for
the knowledge acquired from the underlying text by the
text parser [Hahn et al.1994]. Knowledge in the
initial context is represented
without any explicit qualifications, attachments, provisos, etc. Note that in
the course of text understanding -- due to the working of the basic
hypothesis generation rules (cf. Section "Hypothesis Generation" ) -- a
hypothesis space is created which
contains alternative subspaces for each concept to be
learned, each one holding different or further specialized concept hypotheses.
Various truth-preserving translation rules map
the description of the initial context to
the metacontext which consists of the reified knowledge of
the initial context.
By reification, we mean a
common reflective mechanism, which splits up
a predicative expression into its constituent parts and introduces a
unique anchor term, the reificator, on
which reasoning about this expression, e.g., the annotation by
qualifying assertions, can be based.
This kind of reification is close to the one underlying the FOL system
[Weyhrauch1980,Giunchiglia &
Weyhrauch1988].
Among the reified structures in
the metacontext there is a subcontext embedded, the reified hypothesis
space, the
elements of which carry several qualifications, e.g., reasons to
believe a proposition, indications of consistency,
type and strength of support, etc.
These quality labels result from incremental hypothesis evaluation
and subsequent hypothesis selection, and, thus, reflect the operation
of several second-order qualification rules in the
qualifier ( quality-based classi fier).
The derived labels are the basis for the selection of those
representation structures which are assigned a high degree of
credibility -- only those qualified hypotheses will be
remapped to the hypothesis space of the
initial context by way of (inverse) translation rules.
Thus, we come full circle.
In particular, at the end of each quality-based reasoning cycle the entire
original i-th hypothesis space is replaced by its ( i+1)-th
successor in order to reflect the qualifications computed in the metacontext. The
( i+1)-th hypothesis space is then the input of the
next quality assessment round.
) -- a
hypothesis space is created which
contains alternative subspaces for each concept to be
learned, each one holding different or further specialized concept hypotheses.
Various truth-preserving translation rules map
the description of the initial context to
the metacontext which consists of the reified knowledge of
the initial context.
By reification, we mean a
common reflective mechanism, which splits up
a predicative expression into its constituent parts and introduces a
unique anchor term, the reificator, on
which reasoning about this expression, e.g., the annotation by
qualifying assertions, can be based.
This kind of reification is close to the one underlying the FOL system
[Weyhrauch1980,Giunchiglia &
Weyhrauch1988].
Among the reified structures in
the metacontext there is a subcontext embedded, the reified hypothesis
space, the
elements of which carry several qualifications, e.g., reasons to
believe a proposition, indications of consistency,
type and strength of support, etc.
These quality labels result from incremental hypothesis evaluation
and subsequent hypothesis selection, and, thus, reflect the operation
of several second-order qualification rules in the
qualifier ( quality-based classi fier).
The derived labels are the basis for the selection of those
representation structures which are assigned a high degree of
credibility -- only those qualified hypotheses will be
remapped to the hypothesis space of the
initial context by way of (inverse) translation rules.
Thus, we come full circle.
In particular, at the end of each quality-based reasoning cycle the entire
original i-th hypothesis space is replaced by its ( i+1)-th
successor in order to reflect the qualifications computed in the metacontext. The
( i+1)-th hypothesis space is then the input of the
next quality assessment round.

Figure 1. Architecture for Text Knowledge
Acquisition
FORMAL FRAMEWORK OF QUALITY-BASED
REASONING
Terminological Logic.
We use a standard terminological concept description language,
referred to as 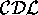 ,
which has several
constructors combining atomic concepts,
roles and individuals to define
the terminological theory of a domain
(for a subset, see Table 1).
,
which has several
constructors combining atomic concepts,
roles and individuals to define
the terminological theory of a domain
(for a subset, see Table 1).

Table 1. Syntax and Semantics for a Subset of 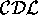

Table 2. 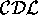 Axioms
Axioms
Concepts are unary predicates, roles
are binary predicates
over a domain  , with
individuals being the elements of
, with
individuals being the elements of  .
We assume a common set-theoretical semantics for
.
We assume a common set-theoretical semantics for 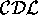 --
an interpretation
--
an interpretation 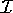 is a function that
assigns to each concept symbol (the set A)
a subset of the domain
is a function that
assigns to each concept symbol (the set A)
a subset of the domain  ,
,
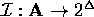 , to each role symbol
(the set P) a binary
relation of
, to each role symbol
(the set P) a binary
relation of  ,
,
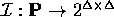 , and
to each individual symbol (the set I)
an element of
, and
to each individual symbol (the set I)
an element of  ,
, 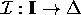 .
Concept terms and role terms are defined inductively.
Table 1 contains corresponding constructors and
their semantics,
where C and D denote concept terms, while R and S
denote roles.
.
Concept terms and role terms are defined inductively.
Table 1 contains corresponding constructors and
their semantics,
where C and D denote concept terms, while R and S
denote roles.
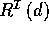 represents the set of
role fillers of the individual d, i.e., the set of individuals e
with
represents the set of
role fillers of the individual d, i.e., the set of individuals e
with
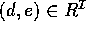 .
.
By means of terminological axioms (for a subset, see Table 2
a symbolic name can be introduced for each concept. It is possible to define
necessary and sufficient constraints (using 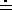 )
or only necessary constraints (using
)
or only necessary constraints (using  ).
A finite set of such axioms
is called the terminology or TBox.
Concepts and roles are associated
with concrete individuals
by assertional axioms (see Table 2;
a,b
denote individuals).
A finite set of such axioms is called the world description or
ABox. An interpretation
).
A finite set of such axioms
is called the terminology or TBox.
Concepts and roles are associated
with concrete individuals
by assertional axioms (see Table 2;
a,b
denote individuals).
A finite set of such axioms is called the world description or
ABox. An interpretation 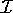 is a model of an ABox
with regard to a TBox, iff
is a model of an ABox
with regard to a TBox, iff 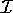 satisfies
the assertional
and terminological axioms. Terminology and world description together
constitute the terminological theory for a given domain.
satisfies
the assertional
and terminological axioms. Terminology and world description together
constitute the terminological theory for a given domain.
Reification.
Let us assume that any hypothesis space H contains a characteristic
terminological theory. In order to reason about that theory
we split up the complex terminological expressions by means of reification.
We here define the (bijective) reification function
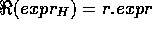 ,
where
,
where 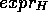 is a terminological expression
known to be true in the hypothesis space H
and
is a terminological expression
known to be true in the hypothesis space H
and 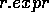 is its corresponding reified
expression, which is composed of
the reificator (an instance of the concept class REIF),
the type of binary relation involved (including INST-OF and
ISA), the relation's domain and range, and the identifier of the
hypothesis space in which the expression holds.
Table 3 gives two definitions for
is its corresponding reified
expression, which is composed of
the reificator (an instance of the concept class REIF),
the type of binary relation involved (including INST-OF and
ISA), the relation's domain and range, and the identifier of the
hypothesis space in which the expression holds.
Table 3 gives two definitions for  ,
more complex ones are provided in schnattinger-et-al95.
By analogy, we may also define
the function
,
more complex ones are provided in schnattinger-et-al95.
By analogy, we may also define
the function  with the corresponding inverse mapping.
with the corresponding inverse mapping.

Table 3. Sketch of the Reification Function 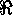
Given the set 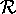 which denotes all
which denotes all 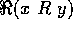 and
the set
and
the set 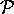 of all instances r of
the class REIF
(i.e.,
of all instances r of
the class REIF
(i.e., 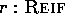 ), we supply the function
), we supply the function
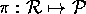 , which maps each
reified expression to the corresponding instance of REIF, i.e., the reificator:
, which maps each
reified expression to the corresponding instance of REIF, i.e., the reificator:
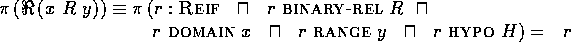
Translation between Contexts.
Translation rules are syntactic transformations which derive
sentences in the metacontext that are equivalent
to sentences in the initial context.
A translation rule from context  to
context
to
context
 is any axiom of the form
is any axiom of the form
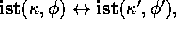 with
with 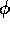 and
and 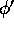 being formulas.
These translation rules are lifting rules in the sense
of McCarthy, as they also relate
the truth in one context to the truth in another one.
being formulas.
These translation rules are lifting rules in the sense
of McCarthy, as they also relate
the truth in one context to the truth in another one.
Instead of supplying a translation rule for each conceptual role
from the set P,
for brevity, we state a single second-order axiom
such that the initial context be translatable to
the metacontext under truth-preserving conditions:
In the metacontext, qualifications can now be expressed instantiating
the specific role QUALIFIED by a qualifying assertion
with respect to some reificator r.
In a similar way, we may construct a translation scheme
which (re)translates the metacontext to the initial context.
This rule incorporates the quality of
some reified element r, which must exceed a specific threshold criterion
(cf. Section "Quality-Based Reasoning with Qualification Rules" ).
).
HYPOTHESIS GENERATION
In the architecture we propose, text parsing and
concept acquisition from texts are tightly coupled. For instance,
whenever two nominals or a nominal and a
verb are supposed to be syntactically related the semantic
interpreter simultaneously evaluates the conceptual compatibility of
the items involved.
Since these reasoning processes are
fully embedded into a terminological knowledge representation system,
checks are being made whether a
concept denoted by one of these objects is allowed to fill a role of
the other one or is
an instance of this concept. If one of the items involved is
unknown, i.e., a lexical and
conceptual gap is encountered, this interpretation mode generates
initial concept hypotheses about
the class membership of the unknown object, and, as a consequence of
inheritance mechanisms holding for concept hierarchies,
provides conceptual role information for the unknown item.
Besides these conceptually rooted computations,
the hypothesis generation process also assigns labels
which indicate the type of
syntactic construction under analysis.
These labels convey information about
the language-specific provenance of the hypotheses
and their individual strength. This idea is motivated by the observation
that syntactic constructions differ in their potential to limit
the conceptual interpretation of an unknown
lexical item. In other words, linguistic structures constrain the range of
plausible inferences
that can be drawn to properly locate their associated concepts
in the domain's concept hierarchy.
For example, an apposition like "the operating system OS/2" doubtlessly
determines the superclass of "OS/2" (here considered as an unknown item)
to be "operating system", while "IBM's OS/2" at best
allows to infer that "OS/2" is one of the products of
IBM (e.g., a computer or a piece of software).
Thus we may stipulate that hypotheses derived from appositions
are more reliable ("certain") than those derived from genitival phrases
only, independent of the conceptual properties being assigned.
The general form of a parser query (cf. also Fig. 1)
triggering the generation of hypotheses is:
query-type (target, base, label), with target being the
unknown
lexical item, base a given knowledge base concept, and label
being the type of syntactic construction which relates base and
target.
In the following, we will concentrate on
two particular instances of query types, viz. those addressing
permitted role fillers and instance-of relations, respectively.

Table 4. Syntactic Qualification Rule PermHypo
The basic assumption behind the first syntactic qualification rule,
PermHypo (Table 4),
is that the target concept fills (exactly) one of the
n roles of the base concept (only those roles are considered which
admit nonnumerical role fillers
and are "non-closed", i.e., still may accept additional role fillers).
Since it cannot be decided on the correct role
yet, n alternative hypotheses are opened (unless additional constraints
apply) and
the target concept is assigned as a potential filler of the i-th role
in its corresponding
hypothesis space. As a result, the classifier is able to derive a
suitable concept hypothesis by specializing
the target concept (initial status "unknown")
according to the value restriction
of the base concept's i-th role.
Additionally, PermHypo assigns a syntactic quality label
to each i-th hypothesis indicating the type of syntactic construction
in which the (lexical counterparts of the) target and base concept
co-occur in the text.
These qualifying assertions are expressed at the terminological level
by linking the reificator of a terminological term via a role QUALIFIED
to a qualifying proposition.
In the syntactic qualification rules described in Tables 4 and 5
the symbol " " separates the
condition part
(starting from the operator EXISTS) from the
action part (containing the TELL operator).
The procedural semantics of the operators FORALL and EXISTS
should be intuitively clear; the operator TELL is used to initiate the
assertion of terminological propositions.
For PermHypo, we assume
" separates the
condition part
(starting from the operator EXISTS) from the
action part (containing the TELL operator).
The procedural semantics of the operators FORALL and EXISTS
should be intuitively clear; the operator TELL is used to initiate the
assertion of terminological propositions.
For PermHypo, we assume 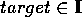 ,
,
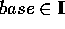 and
and
 =
=  PP-ATTRIBUTION,GENITIVE-ATTRIBUTION,
CASE-FRAME-ASSIGNMENT
PP-ATTRIBUTION,GENITIVE-ATTRIBUTION,
CASE-FRAME-ASSIGNMENT , which is a
subset of the syntactic quality labels.
, which is a
subset of the syntactic quality labels. generate is a function that
-- in the initial context -- either retrieves an already
existing hypothesis space containing a particular terminological assertion, or,
if no such hypothesis space yet exists, creates or
specializes a hypothesis space and asserts a particular
terminological term in this newly constructed hypothesis space. A
transformation rule immediately maps this terminological assertion to
its reified form in the metacontext.
generate is a function that
-- in the initial context -- either retrieves an already
existing hypothesis space containing a particular terminological assertion, or,
if no such hypothesis space yet exists, creates or
specializes a hypothesis space and asserts a particular
terminological term in this newly constructed hypothesis space. A
transformation rule immediately maps this terminological assertion to
its reified form in the metacontext.
The second syntactic qualification rule, SubHypo (Table 5), is triggered if
a target has been encountered in an exemplification phrase
("operating systems like OS/2"),
as part of a compound noun ("WORM technology") or
occurs in an apposition ("the operating system OS/2").
As a consequence, an instance-of relation between
the target and the base item is hypothesized and, in addition, that
syntactic quality label is asserted which indicates the language-specific
construction figuring as the structural source for that hypothesis.
For SubHypo, we assume 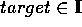 ,
, 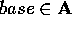 and
and 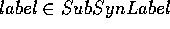 =
=  EXEMPLIFICATION-NP,
NOUN-DECOMPOSITION, APPOSITION-ASSIGNMENT
EXEMPLIFICATION-NP,
NOUN-DECOMPOSITION, APPOSITION-ASSIGNMENT ,
which is another subset of the syntactic quality labels.
,
which is another subset of the syntactic quality labels.

Table 5. Syntactic Qualification Rule SubHypo
QUALITY-BASED REASONING WITH QUALIFICATION RULES
In this section, we will focus on the kind of
quality assessment which occurs at the knowledge base level only;
it is due to the operation of (second-order) conceptual qualification rules.
Within second-order logic we may quantify over relations of
first-order terms, e.g., 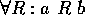 quantifies
over all
roles R which relate a and b.
Our intention is to use
second-order expressions in order to reason about the properties of
terminological descriptions and, thus, to determine the credibility
of various concept hypotheses. Such expressions can be integrated into
the condition part of production
rules in order to generate
qualifying assertions for concept hypotheses.
quantifies
over all
roles R which relate a and b.
Our intention is to use
second-order expressions in order to reason about the properties of
terminological descriptions and, thus, to determine the credibility
of various concept hypotheses. Such expressions can be integrated into
the condition part of production
rules in order to generate
qualifying assertions for concept hypotheses.
Qualifying assertions are the raw data for the computation of quality labels
by the classifier which asserts
INST-OF relations to the corresponding
quality labels (we here only deal with
simple quality labels that are associated with exactly one qualifying role,
though
more complex conditions can be envisaged).
Combining the evidences collected this way
in terms of a quality ranking of concept hypotheses, only
those reified terms that reach a certain credibility threshold
after each quality assessment cycle
are transferred from the metacontext back
to the initial context (cf. Fig.1;
qualified
hypo space in the initial context). Through the use of reification,
we avoid the problems associated with the computational intractability
of second-order logic, and still stay on solid first-order ground.
In the remainder of this section we supply verbal and graphical descriptions of
four conceptual qualification rules. These rules are tested in the
metacontext immediately
after the reification function
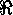 has been applied to some proposition
in the initial context.
The bold portions in the figures indicate
the terminological terms to be qualified, while the lighter ones depict
the qualifying instance.
A detailed example of the working of these rules will be provided in
the next section. A formal description of the rules is given in
hahn-et-al96a.
has been applied to some proposition
in the initial context.
The bold portions in the figures indicate
the terminological terms to be qualified, while the lighter ones depict
the qualifying instance.
A detailed example of the working of these rules will be provided in
the next section. A formal description of the rules is given in
hahn-et-al96a.


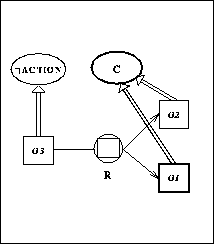

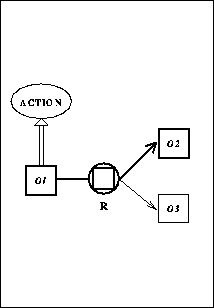

Assessment of Quality Labels.
During each learning step several qualification rules may fire
and thus generate various quality labels. In order to select the
most credible hypotheses from each cycle, we
take the direction (positive/negative) and the individual `strength'
of each label into account by formulating the following
Threshold Criterion:

Ranking of Hypotheses.
Only those hypotheses that continuously reach the credibility threshold
after each quality assessment cycle
are transferred from the metacontext back to the initial context.
At the end of the text analysis a final ranking of
those concept hypotheses is produced
that have repeatedly passed the Threshold Criterion
by applying the following Ranked Prediction Criterion:

A CONCEPT ACQUISITION EXAMPLE
We will now exemplify quality-based terminological reasoning
by considering a concept acquisition task in the domain of
information technology.
As a result of applying syntactic and conceptual qualification rules
different degrees of credibility are assigned to concept
hypotheses and, finally, one hypothesis is selected as the most credible one.
Let us assume the following terminological axioms
(for technical details, cf. Section "Formal Framework of
Quality-Based Reasoning"):

In addition, the following reified assertional axioms are stipulated:


Finally, two verb interpretation rules (for "develop"
and "offer", respectively) are supplied
mapping lexical items onto "conceptually entailed" propositions of
the text knowledge base:

Consider the phrase "Marktanalytiker bestätigen, daß
Compaq seit Jahren erfolgreich LTE-Lites anbietet und
seit kurzem auch Venturas."
Assuming Venturas to be the target concept,
two ambiguities arise (these are rephrased in English terms):
(1) "Market analysts say that Compaq has
been successfully offering LTE-Lites for many years and Venturas
[AGENT] has recently begun to do so as well." vs.
(2) "Market analysts
say that Compaq has been successfully offering LTE-Lites for many years
and has recently begun to offer Venturas [PATIENT] as well.".
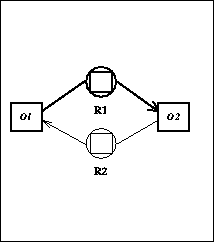
For the first part of the sentence (up to "anbietet" (offer)),
the parser incrementally generates a new instance of OFFER,
assigns Compaq as AGENT and LTE-Lite as PATIENT of
that instance (it has not yet encountered the unknown item Venturas;
a partial graphical representation is given in Fig. 2).
Thus, we get in hypothesis space H0 (fragments of the reified knowledge
structures
are depicted in Fig. 3):
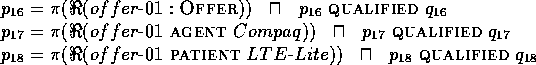
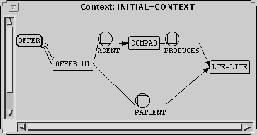
Figure 3. Concept Graph from the Metacontext
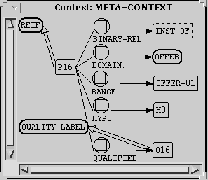
Figure 2. Concept Graph from the Initial Context
The verb interpretation rule for OFFER has no effects, since PRODUCES
is already true ().
As already mentioned, the unknown item Venturas can either be related to LTE-Lite via the
The verb interpretation rule for OFFER has no effects, since
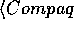 PRODUCES
PRODUCES  is already true
is already true  .
.
As already mentioned, the unknown item Venturas can
either be related to LTE-Lite via the
AGENT role or to Compaq via the PATIENT role of OFFER. This is achieved
by the application of the hypothesis generation
rule PermHypo (Table 4)
that opens two hypothesis subspaces of H0, H1 and H2, for each interpretation of Venturas.
Their reified counterparts, H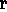 1 and
H
1 and
H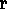 2, are
assigned the
syntactic quality label CASE-FRAME-ASSIGNMENT
(for the ease of readability, we will defer the consideration of
syntactic quality labels in the formal descriptions of the
current example until they contribute
to the discrimination between different hypotheses in later stages of the
sample analysis).
2, are
assigned the
syntactic quality label CASE-FRAME-ASSIGNMENT
(for the ease of readability, we will defer the consideration of
syntactic quality labels in the formal descriptions of the
current example until they contribute
to the discrimination between different hypotheses in later stages of the
sample analysis).
The creation of  (together with
(together with  ) triggers the generation
of two quality labels ADDITIONAL-ROLE-FILLER
according to rule III from the previous section
(note that for both spaces the propositions
) triggers the generation
of two quality labels ADDITIONAL-ROLE-FILLER
according to rule III from the previous section
(note that for both spaces the propositions 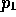 to
to  are assumed to hold).
are assumed to hold).
 ,
,  and
and 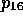 cause the verb
interpretation rule for OFFER to fire
yielding
cause the verb
interpretation rule for OFFER to fire
yielding  . Applying the terminological
axioms for OFFER leads to the deduction of
. Applying the terminological
axioms for OFFER leads to the deduction of  (the AGENT role of
OFFER restricts any of its fillers to
PRODUCER and its taxonomic superconcepts, viz. COMPANY
(
(the AGENT role of
OFFER restricts any of its fillers to
PRODUCER and its taxonomic superconcepts, viz. COMPANY
( ) and
PHYSICAL-OBJECT (
) and
PHYSICAL-OBJECT ( ), by way of
transitive closure).
In particular, H
), by way of
transitive closure).
In particular, H 1,
which covers
the AGENT interpretation contains the
following assertions (
1,
which covers
the AGENT interpretation contains the
following assertions ( to
to  ):
):

On the other hand, H 2
(
2
( to
to  ) covers the PATIENT
interpretation:
) covers the PATIENT
interpretation:

In H 2 all hypotheses
generated
for Venturas (
2 all hypotheses
generated
for Venturas ( to
to  )
receive the quality label SUPPORTED, in H
)
receive the quality label SUPPORTED, in H 1 none.
This support (cf. rule II from the previous section) is
due to the conceptual proximity
1 none.
This support (cf. rule II from the previous section) is
due to the conceptual proximity  and
and
 have relative to
have relative to
 and
and  , respectively. Since both
hypothesis spaces, H1 and H2, imply that Venturas
is at least a PHYSICAL-OBJECT the label MULTIPLY-DEDUCED (rule IV)
is derived in the corresponding reified spaces, H
, respectively. Since both
hypothesis spaces, H1 and H2, imply that Venturas
is at least a PHYSICAL-OBJECT the label MULTIPLY-DEDUCED (rule IV)
is derived in the corresponding reified spaces, H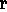 1
and H
1
and H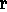 2. Rule III
also triggers in H
2. Rule III
also triggers in H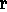 1
and
H
1
and
H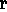 2, so it does not
contribute
to any further discrimination.
2, so it does not
contribute
to any further discrimination.
H2 and thus H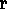 2, however,
can further be refined. According to the
terminological axioms, Compaq -- a
NOTEBOOK-PRODUCER (
2, however,
can further be refined. According to the
terminological axioms, Compaq -- a
NOTEBOOK-PRODUCER (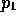 ) -- produces
NOTEBOOKs or ACCUs.
Thus, Venturas, the filler of the PRODUCES role of
Compaq (
) -- produces
NOTEBOOKs or ACCUs.
Thus, Venturas, the filler of the PRODUCES role of
Compaq (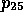 ) must either be a
NOTEBOOK
( H
) must either be a
NOTEBOOK
( H 2
2 )
)
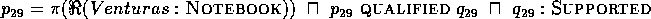
or an ACCU ( H 2
2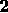 )
)
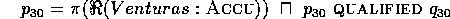
According to this distinction (cf. rule II),
H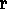 2
2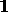 (but not
H
(but not
H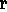 2
2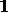 ) is supported by
) is supported by
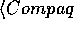 PRODUCES
PRODUCES 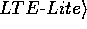 ,
,
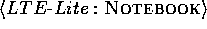 and
and
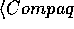 PRODUCES
PRODUCES 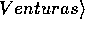 .
.
Since we operate with a partial parser, the linguistic analyses may
remain incomplete due to extra- or ungrammatical input. Assume such a scenario
as in:
"... Venturas ... entwickelt ...
Compaq." ("... Venturas ... develops ...
Compaq.").
The parser triggers the syntactic qualification rule PermHypo
on a presumed case frame assignment for the verb "entwickelt"
(develop). As a result, the
newly generated (reified) hypotheses receive the same
syntactic quality label, viz. CASE-FRAME-ASSIGNMENT.
Due to the value
restrictions that hold for DEVELOP, Compaq ( a priori
known to be a PRODUCER) may only fill the AGENT role.
Correspondingly, in H 1
and
H
1
and
H 2 the following
reified propositions hold:
2 the following
reified propositions hold:
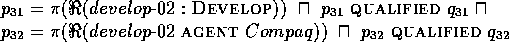
In H1, where Venturas is assumed to be a PRODUCER,
Venturas (additionally to
Compaq) may fill the AGENT role of DEVELOP, leading
to H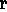 1:
1:

In H2 and the spaces it subsumes, viz. H2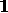 and H2
and H2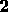 , Venturas may only fill
the PATIENT role. Given the occurrences of
, Venturas may only fill
the PATIENT role. Given the occurrences of 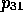 ,
, 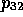 and
and 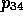 , the verb interpretation
rule for DEVELOP fires and produces
, the verb interpretation
rule for DEVELOP fires and produces 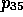 .
This immediately
leads to the generation of a CROSS-SUPPORTED label (rule I from
the previous section) relative to proposition (
.
This immediately
leads to the generation of a CROSS-SUPPORTED label (rule I from
the previous section) relative to proposition (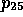 ):
):

Next, one of the interpretations of an ambiguous phrase such as
"Die NiMH-Akkus von Venturas
..." invalidates context H2
invalidates context H2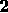 (ACCU hypothesis)
leading to the generation of the (entirely negative) quality label
INCONSISTENT-HYPO in H
(ACCU hypothesis)
leading to the generation of the (entirely negative) quality label
INCONSISTENT-HYPO in H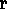 2
2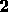 .
The inconsistency is due to the fact that an accumulator cannot be part of
another accumulator.
For the hypothesis space H
.
The inconsistency is due to the fact that an accumulator cannot be part of
another accumulator.
For the hypothesis space H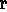 1 we get
1 we get
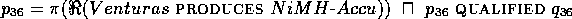
and for H 2 we derive
2 we derive

As a consequence of the
application of the rule PermHypo, the learner assigns to each
reified hypothesis a syntactic label indicating that a prepositional
phrase containing the target
was attached to the base item (label PP-ATTRIBUTION).
Finally, consider the globally ambiguous sentence "Kein Wunder, daß
der Notebook
Venturas auf der Messe prämiert wurde.".
Again, two readings are possible:
(1) "There was no surprise at all that the Venturas notebook had been
awarded at the fare" and (2) "There was no surprise at all that the
notebook from [the manufacturer] Venturas had been awarded at the fare".
Considering the first reading which implies VENTURAS to be a
notebook, the SubHypo qualification rule (cf. Table 5)
is triggered and assigns the (strong) syntactic label APPOSITION-ASSIGNMENT to
proposition 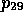 from hypothesis space H
from hypothesis space H 2
2 .
.
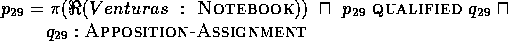
On the other hand, the second
reading (genitive phrase attachment) invokes the PermHypo rule
and the assignment of the (weaker) syntactic label GENITIVE-ATTRIBUTION
to proposition 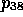 . Note that the
referent of "der Notebook
Venturas" ( the notebook from Venturas) has been resolved to
. Note that the
referent of "der Notebook
Venturas" ( the notebook from Venturas) has been resolved to
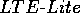 by the anaphor
resolution component of our parser (strube95
strube95). This reference
resolution process is legitimated by hypothesis
by the anaphor
resolution component of our parser (strube95
strube95). This reference
resolution process is legitimated by hypothesis 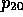 of H
of H 1,
viz. (Venturas PRODUCES
1,
viz. (Venturas PRODUCES 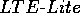 ). Thus,
we get for H
). Thus,
we get for H 1:
1:
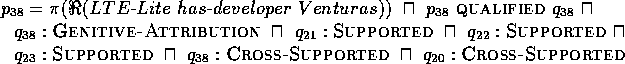
Note that in our example we now encounter for the first time
two different syntactic labels as derived from the same
verbal input. This is due to the global ambiguity of
the
sentence. Up to this point, all reified hypothesis spaces have received the
same type and number of syntactic quality labels (i.e., CASE-FRAME-ASSIGNMENT (2)
and PP-ATTRIBUTION (1), respectively).
Hence, considering only syntactic evaluation criteria,
a ranking of hypotheses based on the syntactic quality labels would
prefer H2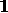 over H1,
since the label APPOSITION-ASSIGNMENT
(from H
over H1,
since the label APPOSITION-ASSIGNMENT
(from H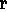 2
2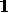 ) is stronger than the label
GENITIVE-ATTRIBUTION (from H
) is stronger than the label
GENITIVE-ATTRIBUTION (from H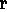 1),
all other labels being equal.
1),
all other labels being equal.
Considering the collection of conceptual quality labels we have
derived,
this preliminary preference is further supported.
The most promising hypothesis space is
H2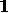 (covering the NOTEBOOK
reading for Venturas)
whose reified counterpart holds 10 positive labels: MULTIPLY-DEDUCED (1),
SUPPORTED (8), CROSS-SUPPORTED (1),
(covering the NOTEBOOK
reading for Venturas)
whose reified counterpart holds 10 positive labels: MULTIPLY-DEDUCED (1),
SUPPORTED (8), CROSS-SUPPORTED (1), but only one negative label
(ADDITIONAL-ROLE-FILLER). In contrast, H2
but only one negative label
(ADDITIONAL-ROLE-FILLER). In contrast, H2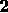 is ruled out,
since an inconsistency has been detected by the classifier. Finally,
H
is ruled out,
since an inconsistency has been detected by the classifier. Finally,
H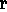 1
(holding the PRODUCER interpretation for Venturas) has
received a weaker level of confirmation ---
MULTIPLY-DEDUCED (1), SUPPORTED (3),
CROSS-SUPPORTED (1), and ADDITIONAL-ROLE-FILLER (2) --- and H1 is,
therefore, less
plausible than H2
1
(holding the PRODUCER interpretation for Venturas) has
received a weaker level of confirmation ---
MULTIPLY-DEDUCED (1), SUPPORTED (3),
CROSS-SUPPORTED (1), and ADDITIONAL-ROLE-FILLER (2) --- and H1 is,
therefore, less
plausible than H2 (cf. also the "Ranked Prediction Criterion" in Section "Quality-Based
Reasoning with Qualification Rules").
Summarizing our sample analysis, we, finally,
have strong indications for choosing
hypothesis H2
(cf. also the "Ranked Prediction Criterion" in Section "Quality-Based
Reasoning with Qualification Rules").
Summarizing our sample analysis, we, finally,
have strong indications for choosing
hypothesis H2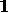 over H1
based on conceptual and
syntactic assessment criteria, since they both point into the same
direction
(which, of course, needs not always be the case).
over H1
based on conceptual and
syntactic assessment criteria, since they both point into the same
direction
(which, of course, needs not always be the case).
The preference aggregation
scheme we have just sketched is based on a solid formal decision procedure
which outweighs the contributions of different types and numbers of
quality labels (cf. schnattinger-hahn96).
EMPIRICAL EVALUATION
While major theoretical principles of our approach have already been
previously published [Hahn et al.1996a,Hahn et al.1996b],
our model, so far, lacked a serious empirical justification.
In this section, we present some empirical data from a preliminary evaluation
of the quality-based concept learner.
In these experiments we focus on the issues of learning accuracy
and the learning rate.
Due to the given learning environment, the measures we apply
deviate from those commonly used in machine learning approaches to
concept learning. In concept learning algorithms like IBL [Aha et al.1991]
there is no hierarchy of concepts. Hence, any prediction of the class
membership of a new instance is either true or false. However, given
such a hierarchy, a prediction can be more or less precise, i.e.,
it may approximate the goal concept at different levels of specificity.
This is captured by our measure of learning
accuracy which takes into account the conceptual distance of a
hypothesis to the goal concept of an instance , rather than
simply
relate the number of correct and false predictions, as in IBL.
, rather than
simply
relate the number of correct and false predictions, as in IBL.
In our approach learning is achieved by the refinement of
multiple hypotheses about the class membership of an
instance. Thus, the measure of learning rate we propose is concerned
with the
reduction rate of hypotheses as more and more information
becomes available about one particular new instance. In contrast, IBL-style
algorithms consider
only one concept hypothesis per learning cycle and their notion of
learning rate relates
to the increase of correct predictions as more and more
instances are being processed.
Altogether we considered 18 texts which contained 6344 tokens.
The input for the learner were terminological assertions representing
the semantic interpretation of the sentences as exemplified by Fig. 2
(cf. Section "A Concept Acquisition Example").
Learning Accuracy
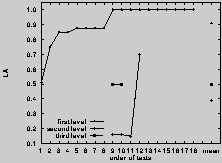
Figure 5. Impact of the Qualification Calculus on the Learning Accuracy
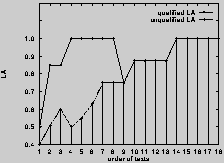
Figure 4. Learning Accuracy at Different Prediction Levels
In a first sequence of experiments we investigated the learning
accuracy
of the system, i.e., the degree to which the system correctly predicts
the concept class which subsumes (realizes) the target concept under
consideration.
The following parameters relate to the discussion of
the learning accuracy:
-
the number of hypothesis spaces at the end of the text analysis ( HSTA);
-
the number of hypothesis spaces after qualification ( HSQAL)
(cf. the "Threshold Criterion" from Section
"Quality-Based Reasoning with Qualification Rules"),
using the "optimal" configuration of qualification criteria
(Fig. 4 contains the empirical data to
determine the
optimal design);
-
the correct TARGET concept to be learned
(supplied by a human experimentator
on the basis of introspective understanding of the chosen texts);
-
a (partial) ordering of system-generated predictions ( PRED)
based on the "Ranked Prediction Criterion" of the qualification calculus
(cf. Section "Quality-Based Reasoning with Qualification Rules").
Learning accuracy (LA) is defined as:
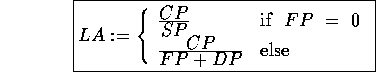
where SP specifies the length of the shortest path (in terms of
the number of nodes
traversed) from the TOP node of the concept hierarchy to the
maximally specific concept subsuming (realizing) the instance to be learned;
CP specifies the length of the path from the TOP node to that
concept node which is common both for the shortest path
(as defined above) and
the actual path to the predicted concept (whether correct or not);
FP specifies the length of
the path from the TOP node to the predicted
(in this case false) concept and
DP denotes the distance between the predicted node and the most
specific
concept correctly subsuming the target instance.
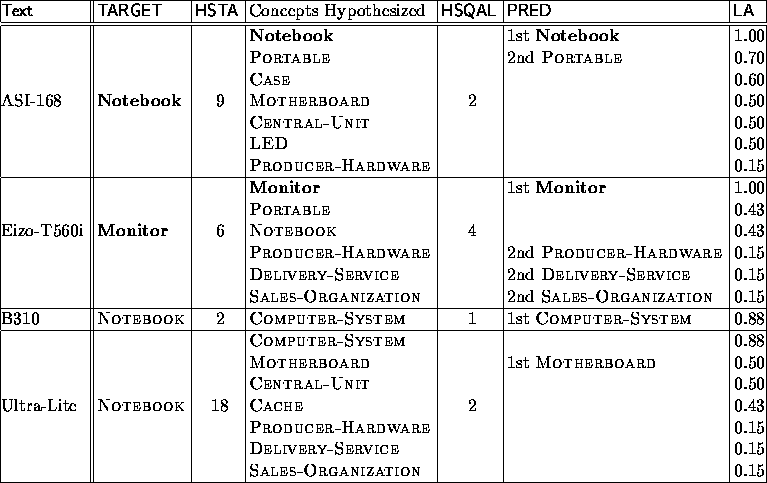
Table 6. Summary of Some Concept Learning Results
Most of these parameters appear in Table 6
which summarizes the learning data for four different texts.
The first two rows depict correct predictions (texts about "ASI-168"
and "Eizo-T560i"), the first one with an significant reduction rate
for the hypothesis spaces, the second with plenty of (low-valued second-order)
predictions. Text "B310" illustrates a near miss (the target NOTEBOOK
has only been narrowed down to COMPUTER-SYSTEM; cf. also the
corresponding accuracy rate), while the final text "Ultra-Lite" gives
an example of a "false" prediction (however, correct up to the level of
HARDWARE).
As the system provides a ranking of learning hypotheses
(cf. the PRED column in Table 6)
we investigated the optimal choice of rankings.
Fig. 4 gives the accuracy graph for
the different rankings produced by the learner.
We considered each level of predictions
(up to the third; based on the application of the "Ranked Prediction
Criterion") independently
for each text and, finally, determined its mean accuracy
for each level
(91% (18), 39% (4), 50% (2) for first-, second-, and third-order
prediction, respectively; absolute numbers of cases are in brackets).
The mean values
for second- and third-order predictions should be considered with care
as the base number of cases is terribly low.
In 14 of the 18 cases the "Threshold Criterion" reduces the number of
concept hypotheses to 1; hence only few second- and third-order
predictions
were generated
(we interpret this finding as an indication
of confidence in the underlying quality-based reasoning mechanisms).
Since none of the (admittedly low numbers of) second- and third-order
predictions ever exceeded the accuracy value of the
prediction at the first level, the "Ranked Prediction Criterion" seems
discriminative already at this top level.
So we may conclude that choosing only the
first level of predictions yields the highest benefits.
In order to illustrate the contribution of the qualification calculus
on the learning accuracy achieved, Fig. 5 depicts
the average accuracy value including (solid upper line)
the qualification rules
and without (dotted lower line), i.e., no "Threshold" and no "Ranked
Prediction Criterion" (cf. Section "Quality-Based Reasoning with Qualification
Rules") were applied,
though the usual terminological reasoning facilities still were used.
Learning Rate
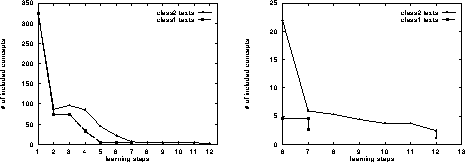
Figure 6. Mean Number of Included Concepts per Learning
Step
The learning accuracy focuses on the final result of the learning process.
By considering the learning rate, we supply background data from
the step-wise development of the learning process.
Fig. 6 contains the mean number of transitively
included
concepts for all considered hypothesis spaces per learning step
(each concept hypothesis denotes a concept which transitively
subsumes various subconcepts).
Note that the most general concept hypothesis
denotes TOP and, therefore, includes the entire knowledge base
(currently, 340 concepts).
We grouped the 18 texts into two classes in order to normalize the number
of propositions they contained ,
viz. one ranging from 7 to 11 ( class 1,
reductionto 7 propositions),
the other ranging from 12 to 25 propositions ( class 2, reduction
to 12 propositions). The left graph in Fig. 6 gives
the
overall
mean learning rate for both classes. The right one
(zooming at the learning steps 6 to 12) focuses on
the reduction achieved by the qualification calculus, yielding a final
drop
of approximately 50% (class 1: from 4.9 to 2.6 concepts, class 2:
from 3.7 to 1.9).
,
viz. one ranging from 7 to 11 ( class 1,
reductionto 7 propositions),
the other ranging from 12 to 25 propositions ( class 2, reduction
to 12 propositions). The left graph in Fig. 6 gives
the
overall
mean learning rate for both classes. The right one
(zooming at the learning steps 6 to 12) focuses on
the reduction achieved by the qualification calculus, yielding a final
drop
of approximately 50% (class 1: from 4.9 to 2.6 concepts, class 2:
from 3.7 to 1.9).
Summarizing this preliminary evaluation experiment,
the quality-based learning system
yields competitive accuracy rates (a mean of 91%;
cf. Fig. 4), exhibits significant and valid
reductions
of the hypothesis spaces (cf. Fig. 6) based on the
working
of the qualification calculus (cf. Fig. 5).
RELATED WORK
Our approach bears a close relationship to the work of
Mooney [1987]
Martin [1992]
and Hastings [1992],
who aim at the automated learning of word meanings and their
underlying concepts from context.
But our work differs from theirs in that
the need to cope with several competing concept
hypotheses is not an issue in these studies.
Considering, however, the limitations almost
any parser available for realistic
text understanding tasks currently suffers from
(finally leading to the generation of partial parses only),
usually multiple concept hypotheses will be derived
from a given natural language input.
Therefore, we stress the
need for a hypothesis generation and evaluation component as an integral
part of any robust natural language system that
learns in tandem with such coverage-restricted devices.
Other systems aiming at text knowledge acquisition differ from our approach in
that they either rely on hand-coded input [Skuce et
al.1985]
or use overly simplistic keyword-based content analysis techniques
[Agarwal & Tanniru1991],
are restricted to a deductive learning mode [Handa
& Ishizaki1989],
use quantitative measures for uncertainty to evaluate
the confidence of learned concept descriptions
(as the WIT system, cf. Reimer [1990]),
or lack the continuous refinement property of pursuing alternative hypotheses
(as the SNOWY system, cf. Gomez [1990],
Gomez [1995]).
Nevertheless, WIT and SNOWY are closest to our approach,
at least with respect to the text understanding methodologies being used,
namely, the processing of realistic texts
and the acquisition of taxonomic knowledge structures with the aid of a
terminological representation system.
As WIT uses a partial parser similar to our approach,
learning results are also uncertain and their confidence level
needs to be recorded for
evaluation purposes. However, WIT uses a quantitative approach to evaluate
the confidence of learned concept descriptions, while we prefer a qualitative
method which is fully embedded into the terminological reasoning process
underlying text understanding. This allows us to reason about the conditions
which led to the creation
and the further refinement of concept hypotheses in terms of quality assessment.
SNOWY is a knowledge acquisition system that processes real-world
texts and builds up a taxonomic knowledge base that can be used in
classification-based problem solving.
In contrast to our system, SNOWY is domain-independent, i.e., it uses no
domain-specific background knowledge for text understanding and
knowledge acquisition. As a consequence,
SNOWY has no means for a knowledge-based assessment of new hypotheses.
This is in contrast to our approach, in which conceptual qualification rules
are incrementally applied to judge the quality of new and alternative hypotheses
given a sufficient domain theory.
The processing of written texts can, in general, be considered
a major step towards the automation of knowledge acquisition [Virkar & Roach1989]
which, so far, has been dominated by interactive modes
in a dialogue setting,
e.g., KALEX [Schmidt & Wetter1989] or AKE
[Gao & Salveter1991].
CONCLUSIONS
We have introduced
a methodology for automated knowledge acquisition and learning from texts that
relies upon
terminological (meta)reasoning.
Concept hypotheses
which have been derived in the course of the text understanding process
are assigned specific "quality labels" (indicating their
significance, reliability, strength).
Quality assessment of hypotheses accounts for
conceptual criteria referring to their given knowledge base context
as well as linguistic indicators (grammatical constructions, discourse patterns),
which led to their generation.
Metareasoning, as we conceive it, is based on the reification of
terminological expressions, the assignment of
qualifications to these reified structures, and the reasoning about
degrees of credibility these qualifications give rise to based on the
evaluation of first-order syntactic and second-order conceptual
qualification rules.
Thus, the metareasoning approach we advocate allows for the
quality-based evaluation and a bootstrapping-style selection of alternative
concept hypotheses as text understanding incrementally proceeds.
A major constraint underlying our work is that
this kind of quality-based metareasoning -- through the use of reification
mechanisms --
is completely embedded in the homogeneous framework of standard first-order
terminological reasoning systems using multiple contexts, so that we
may profit from their full-blown classification mechanisms.
The applicability of this terminological metareasoning framework
has been shown for a concept acquisition task
in the framework of realistic text understanding.
We are currently
focusing on the formulation of additional qualification rules
and query types,
the formalization of a qualification calculus which captures the evaluation
logic of multiple quality labels within a terminological
framework [Schnattinger &
Hahn1996], and an in-depth empirical
evaluation of our approach based
on a larger corpus of texts. The knowledge acquisition and
learning system described in this paper has been fully
implemented in LOOM [MacGregor1994].
Acknowledgments.
This work was partially supported by
grants from DFG under the account Ha 2097/2-1 and Ha 2097/3-1.
We like to thank the members of our group for fruitful discussions.
We also gratefully acknowledge the provision of the LOOM system from USC/ISI.
References
- Agarwal & Tanniru1991
-
Agarwal, R. & M. Tanniru (1991).
Knowledge extraction using content analysis.
Knowledge Acquisition, 3(4):421--441.
- Aha et al.1991
-
Aha, D., D. Kibler & M. Albert (1991).
Instance-based learning algorithms.
Machine Learning, 6:37--66.
- Gao & Salveter1991
-
Gao, Y. & S. Salveter (1991).
The automated knowledge engineer: Natural language knowledge
acquisition for expert systems.
In KAW'91 - Proc. of the 6th Knowledge Acquisition for
Knowledge-Based Systems Workshop. Banff, Canada.
- Giunchiglia &
Weyhrauch1988
-
Giunchiglia, F. & R. Weyhrauch (1988).
A multi-context monotonic axiomatization of inessential
non-monotonicity.
In P. Maes & D. Nardi (Eds.), Meta-Level Architectures and
Reflection, pp. 271--285. Amsterdam: North-Holland.
- Gomez1995
-
Gomez, F. (1995).
Acquiring knowledge about the habitats of animals from encyclopedic
texts.
In KAW'95 - Proc. of the Workshop on Knowledge Acquisition for
Knowledge-Based Systems.
- Gomez & Segami1990
-
Gomez, F. & C. Segami (1990).
Knowledge acquisition from natural language for expert systems based
on classification problem-solving methods.
Knowledge Acquisition, 2(2):107--128.
- Hahn et al.1996a
-
Hahn, U., M. Klenner & K. Schnattinger (1996a).
Learning from texts: A terminological metareasoning perspective.
In S. Wermter, E. Riloff & G. Scheler (Eds.), Connectionist,
Statistical and Symbolic Approaches to Learning in Natural Language
Processing, pp. 453--468. Berlin: Springer.
- Hahn et al.1996b
-
Hahn, U., M. Klenner & K. Schnattinger (1996b).
A quality-based terminological reasoning model for text knowledge
acquisition.
In N. Shadbolt, K. O'Hara & G. Schreiber (Eds.), Advances in
Knowledge Acquisition. Proc. of the 9th European Knowledge Acquisition
Workshop (EKAW '96), pp. 131--146. Berlin: Springer.
- Hahn et al.1994
-
Hahn, U., S. Schacht & N. Bröker (1994).
Concurrent, object-oriented dependency parsing: The PARSETALK
model.
International Journal of Human-Computer Studies,
41(1-2):179--222.
- Hahn et al.1996c
-
Hahn, U., K. Schnattinger & M. Romacker (1996c).
Automatic knowledge acquisition from medical texts.
In J. Cimino (Ed.), AMIA'96 - Proc. of the 1996 AMIA Fall
Symposium (formerly SCAMC). Washington, D.C., October 26-30, 1996.
Philadelphia, PA: Hanely & Belfus.
- Hahn & Strube1996
-
Hahn, U. & M. Strube (1996).
PARSETALK about functional anaphora.
In G. McCalla (Ed.), Advances in Artificial Intelligence. Proc.\
of the 11th Biennial Conf. of the Canadian Society for Computational Studies
of Intelligence (AI'96), pp. 133--145. Toronto, Ontario, Canada, May
21-24,
1996. Berlin: Springer.
- Handa & Ishizaki1989
-
Handa, K. & S. Ishizaki (1989).
Acquiring knowledge about a relation between concepts.
In EKAW'89 - Proc. of the ds.), Connectionist,
Statistical and Symbolic Approaches to Learning in Natural Language
Processing, pp. 261--274. Berlin: Springer.
- Hastings & Lytinen1994
-
Hastings, P.M. & S.L. Lytinen (1994).
The ups and downs of lexical acquisition.
In AAAI'94 - Proc. of the 12th National Conf. on Artificial
Intelligence. Vol. 2, pp. 754--759. Menlo Park: AAAI Press/MIT Press.
- Lewis1991
-
Lewis, D. (1991).
Learning in intelligent information retrieval.
In L. Birnbaum & G. Collins (Eds.), Machine Learning: Proc.\
of the 8th Intl. Workshop, pp. 235--239. San Mateo/CA: Morgan Kaufmann.
- MacGregor1994
-
MacGregor, R.M. (1994).
A description classifier for the predicate calculus.
In AAAI'94 - Proc. of the 12th National Conf. on Artificial
Intelligence. Vol. 1, pp. 213--220. Menlo Park: AAAI Press/MIT Press.
- Martin1992
-
Martin, W. (1992).
Concept-oriented parsing of definitions.
In COLING'92 - Proc. of the 15th Intl. Conf. on Computational
Linguistics, pp. 988--992.
- McCarthy1993
-
McCarthy, J. (1993).
Notes on formalizing context.
In IJCAI'93 - Proc. of the 13th Intl. Joint Conf. on
Artificial Intelligence. Vol. 1, pp. 555--560. San Mateo, CA: Morgan
Kaufmann.
- Mooney1987
-
Mooney, R. (1987).
Integrated learning of words and their underlying concepts.
In Proc. of the 9th Annual Conf. of the Cognitive Science
Society, pp. 974--978. Hillsdale, NJ: L. Erlbaum.
- Reimer1990
-
Reimer, U. (1990).
Automatic knowledge aquisition from texts: Learning terminological
knowledge via text understanding and inductive generalization.
In KAW'90 - Proc. of the Workshop on Knowledge Acquisition for
Knowledge-Based Systems, pp. 27.1--27.16.
- Resnik1992
-
Resnik, P. (1992).
A class-based approach to lexical discovery.
In Proc. of the 30th Annual Meeting of the Association for
Computational Linguistics, pp. 327--329. Newark, Delaware, USA, 28 June -
2
July 1992.
- Schmidt & Wetter1989
-
Schmidt, G. & T. Wetter (1989).
Towards knowledge acquisition in natural language dialogue.
In EKAW'89 - Proc. of the European Knowledge Acquisition
Workshop, pp. 239--252.
- Schnattinger &
Hahn1996
-
Schnattinger, K. & U. Hahn (1996).
A sketch of a qualification calculus.
In FLAIRS'96 - Proc. of the 9th Florida AI Research Symposium,
pp. 198--203. Key West, Florida, May 20-22, 1996.
- Schnattinger
et al.1995
-
Schnattinger, K., U. Hahn & M. Klenner (1995).
Terminological meta-reasoning by reification and multiple contexts.
In Progress in Artificial Intelligence. Proc. of the 7th
Portuguese Conf. on Artificial Intelligence (EPIA '95), pp. 1--16. Berlin:
Springer.
- Sekine et al.1992
-
Sekine, S., J. Carroll, S. Ananiadou & J. Tsujii (1992).
Automatic learning for semantic collocation.
In Proc. of the 3rd Conf. on Applied Natural Language
Processing, pp. 104--110. Trento, Italy, 31 March - 3 April 1992.
- Skuce et al.1985
-
Skuce, D., S. Matwin, B. Tauzovich, F. Oppacher & S. Szpakowicz (1985).
A logic-based knowledge source system for natural language documents.
Data & Knowledge Engineering, 1(3):201--231.
- Strube & Hahn1995
-
Strube, M. & U. Hahn (1995).
PARSETALK about sentence- and text-level anaphora.
In EACL'95 - Proc. of the 7th Conf. of the European Chapter of
the Association for Computational Linguistics, pp. 237--244. Dublin,
Ireland, March 27-31, 1995.
- Virkar & Roach1989
-
Virkar, R. & J. Roach (1989).
Direct assimilation of expert-level knowledge by automatically
parsing research paper abstracts.
International Journal of Expert Systems, 1(4):281--305.
- Weyhrauch1980
-
Weyhrauch, R.W. (1980).
Prolegomena to a theory of mechanized formal reasoning.
Artificial Intelligence, 13(1):133--170.
- Woods & Schmolze1992
-
Woods, W. & J. Schmolze (1992).
The KL-ONE family.
Computers & Mathematics with Applications, 23(2-5):133--177.
- ...labels.
-
Note that the base and the target object are instances, rather than
concepts in the terminological sense. The reason for this restriction
is merely an implementational one.
Almost every terminological system we know about is not able to
incrementally update concept descriptions during run-time.
The concept acquisition methodology we propose is, however,
not restricted to mere instance learning, in principle.
The learning procedure just treats instances as well as concept classes
in the same way (technically, both kinds of terminological objects
are considered ABox elements).
- ...discrimination.
-
We only consider the derivation of quality labels
referring to the target concept and leave away those
labels that support propositions already contained in the
a priori knowledge of the KB kernel.
- ......"
- "The NiMH accus as part of the
Venturas..." provokes an inconsistency;
this reading is opposed to "The NiMH accus supplied by
Venturas...".
- ...(1),
-
Only those quality labels are considered
which refer to the concept hypotheses under consideration.
Quality labels which relate to a priori known concepts are simply
discarded (namely, 171#171
and 172#172).
- ...instance
- In a companion paper [Hahn & Strube1996], we argue for the
adequacy of
conceptual distance measures for network-based knowledge representation
structures under certain ontological engineering assumptions.
- ...contained
-
By normalization with respect to the number of propositions
we account for the fact that each text is characterized by
a specific number of learning steps per unknown concept.
The result of a learning step is either a refinement
of the concept to be learned or a confirmation
of the current state of the concept description.
In order to compare texts with varying numbers of learning steps
we grouped those texts together which exhibited a common
behavior with respect to the confirmation of concept hypotheses
(i.e., they did no longer change at all;
this usually happens at the very end of the learning process)
by simply eliminating learning steps which exhibit simple
confirmation behavior. This coincides with empirical evidence
we have collected for the fact that the proposed learning procedure
quite rapidly finds the relevant discriminations
which then tend to be continuously confirmed during the remaining
learning process.
Klemens Schnattinger
 ) -- a
hypothesis space is created which
contains alternative subspaces for each concept to be
learned, each one holding different or further specialized concept hypotheses.
Various truth-preserving translation rules map
the description of the initial context to
the metacontext which consists of the reified knowledge of
the initial context.
By reification, we mean a
common reflective mechanism, which splits up
a predicative expression into its constituent parts and introduces a
unique anchor term, the reificator, on
which reasoning about this expression, e.g., the annotation by
qualifying assertions, can be based.
This kind of reification is close to the one underlying the FOL system
[Weyhrauch1980,Giunchiglia &
Weyhrauch1988].
Among the reified structures in
the metacontext there is a subcontext embedded, the reified hypothesis
space, the
elements of which carry several qualifications, e.g., reasons to
believe a proposition, indications of consistency,
type and strength of support, etc.
These quality labels result from incremental hypothesis evaluation
and subsequent hypothesis selection, and, thus, reflect the operation
of several second-order qualification rules in the
qualifier ( quality-based classi fier).
The derived labels are the basis for the selection of those
representation structures which are assigned a high degree of
credibility -- only those qualified hypotheses will be
remapped to the hypothesis space of the
initial context by way of (inverse) translation rules.
Thus, we come full circle.
In particular, at the end of each quality-based reasoning cycle the entire
original i-th hypothesis space is replaced by its ( i+1)-th
successor in order to reflect the qualifications computed in the metacontext. The
( i+1)-th hypothesis space is then the input of the
next quality assessment round.
) -- a
hypothesis space is created which
contains alternative subspaces for each concept to be
learned, each one holding different or further specialized concept hypotheses.
Various truth-preserving translation rules map
the description of the initial context to
the metacontext which consists of the reified knowledge of
the initial context.
By reification, we mean a
common reflective mechanism, which splits up
a predicative expression into its constituent parts and introduces a
unique anchor term, the reificator, on
which reasoning about this expression, e.g., the annotation by
qualifying assertions, can be based.
This kind of reification is close to the one underlying the FOL system
[Weyhrauch1980,Giunchiglia &
Weyhrauch1988].
Among the reified structures in
the metacontext there is a subcontext embedded, the reified hypothesis
space, the
elements of which carry several qualifications, e.g., reasons to
believe a proposition, indications of consistency,
type and strength of support, etc.
These quality labels result from incremental hypothesis evaluation
and subsequent hypothesis selection, and, thus, reflect the operation
of several second-order qualification rules in the
qualifier ( quality-based classi fier).
The derived labels are the basis for the selection of those
representation structures which are assigned a high degree of
credibility -- only those qualified hypotheses will be
remapped to the hypothesis space of the
initial context by way of (inverse) translation rules.
Thus, we come full circle.
In particular, at the end of each quality-based reasoning cycle the entire
original i-th hypothesis space is replaced by its ( i+1)-th
successor in order to reflect the qualifications computed in the metacontext. The
( i+1)-th hypothesis space is then the input of the
next quality assessment round.

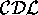 ,
which has several
constructors combining atomic concepts,
roles and individuals to define
the terminological theory of a domain
(for a subset, see Table 1).
,
which has several
constructors combining atomic concepts,
roles and individuals to define
the terminological theory of a domain
(for a subset, see Table 1).

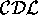

 , with
individuals being the elements of
, with
individuals being the elements of  .
We assume a common set-theoretical semantics for
.
We assume a common set-theoretical semantics for 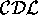 --
an interpretation
--
an interpretation 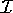 is a function that
assigns to each concept symbol (the set A)
a subset of the domain
is a function that
assigns to each concept symbol (the set A)
a subset of the domain  ,
,
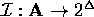 , to each role symbol
(the set P) a binary
relation of
, to each role symbol
(the set P) a binary
relation of  ,
,
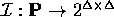 , and
to each individual symbol (the set I)
an element of
, and
to each individual symbol (the set I)
an element of  ,
, 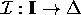 .
Concept terms and role terms are defined inductively.
Table 1 contains corresponding constructors and
their semantics,
where C and D denote concept terms, while R and S
denote roles.
.
Concept terms and role terms are defined inductively.
Table 1 contains corresponding constructors and
their semantics,
where C and D denote concept terms, while R and S
denote roles.
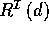 represents the set of
role fillers of the individual d, i.e., the set of individuals e
with
represents the set of
role fillers of the individual d, i.e., the set of individuals e
with
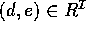 .
.
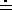 )
or only necessary constraints (using
)
or only necessary constraints (using 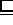 ).
A finite set of such axioms
is called the terminology or TBox.
Concepts and roles are associated
with concrete individuals
by assertional axioms (see Table 2;
a,b
denote individuals).
A finite set of such axioms is called the world description or
ABox. An interpretation
).
A finite set of such axioms
is called the terminology or TBox.
Concepts and roles are associated
with concrete individuals
by assertional axioms (see Table 2;
a,b
denote individuals).
A finite set of such axioms is called the world description or
ABox. An interpretation 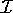 is a model of an ABox
with regard to a TBox, iff
is a model of an ABox
with regard to a TBox, iff 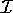 satisfies
the assertional
and terminological axioms. Terminology and world description together
constitute the terminological theory for a given domain.
satisfies
the assertional
and terminological axioms. Terminology and world description together
constitute the terminological theory for a given domain.
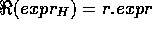 ,
where
,
where 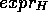 is a terminological expression
known to be true in the hypothesis space H
and
is a terminological expression
known to be true in the hypothesis space H
and 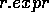 is its corresponding reified
expression, which is composed of
the reificator (an instance of the concept class REIF),
the type of binary relation involved (including INST-OF and
ISA), the relation's domain and range, and the identifier of the
hypothesis space in which the expression holds.
Table 3 gives two definitions for
is its corresponding reified
expression, which is composed of
the reificator (an instance of the concept class REIF),
the type of binary relation involved (including INST-OF and
ISA), the relation's domain and range, and the identifier of the
hypothesis space in which the expression holds.
Table 3 gives two definitions for  ,
more complex ones are provided in schnattinger-et-al95.
By analogy, we may also define
the function
,
more complex ones are provided in schnattinger-et-al95.
By analogy, we may also define
the function  with the corresponding inverse mapping.
with the corresponding inverse mapping.

 which denotes all
which denotes all 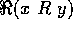 and
the set
and
the set  of all instances r of
the class REIF
(i.e.,
of all instances r of
the class REIF
(i.e., 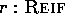 ), we supply the function
), we supply the function
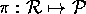 , which maps each
reified expression to the corresponding instance of REIF, i.e., the reificator:
, which maps each
reified expression to the corresponding instance of REIF, i.e., the reificator:
 to
context
to
context
 is any axiom of the form
is any axiom of the form
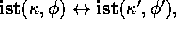 with
with 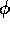 and
and 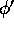 being formulas.
These translation rules are lifting rules in the sense
of McCarthy, as they also relate
the truth in one context to the truth in another one.
being formulas.
These translation rules are lifting rules in the sense
of McCarthy, as they also relate
the truth in one context to the truth in another one.

 " separates the
condition part
(starting from the operator EXISTS) from the
action part (containing the TELL operator).
The procedural semantics of the operators FORALL and EXISTS
should be intuitively clear; the operator TELL is used to initiate the
assertion of terminological propositions.
For PermHypo, we assume
" separates the
condition part
(starting from the operator EXISTS) from the
action part (containing the TELL operator).
The procedural semantics of the operators FORALL and EXISTS
should be intuitively clear; the operator TELL is used to initiate the
assertion of terminological propositions.
For PermHypo, we assume 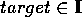 ,
,
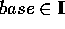 and
and
 =
=  PP-ATTRIBUTION,GENITIVE-ATTRIBUTION,
CASE-FRAME-ASSIGNMENT
PP-ATTRIBUTION,GENITIVE-ATTRIBUTION,
CASE-FRAME-ASSIGNMENT , which is a
subset of the syntactic quality labels.
, which is a
subset of the syntactic quality labels.
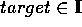 ,
, 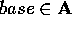 and
and 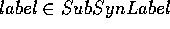 =
=  EXEMPLIFICATION-NP,
NOUN-DECOMPOSITION, APPOSITION-ASSIGNMENT
EXEMPLIFICATION-NP,
NOUN-DECOMPOSITION, APPOSITION-ASSIGNMENT ,
which is another subset of the syntactic quality labels.
,
which is another subset of the syntactic quality labels.

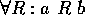 quantifies
over all
roles R which relate a and b.
Our intention is to use
second-order expressions in order to reason about the properties of
terminological descriptions and, thus, to determine the credibility
of various concept hypotheses. Such expressions can be integrated into
the condition part of production
rules in order to generate
qualifying assertions for concept hypotheses.
quantifies
over all
roles R which relate a and b.
Our intention is to use
second-order expressions in order to reason about the properties of
terminological descriptions and, thus, to determine the credibility
of various concept hypotheses. Such expressions can be integrated into
the condition part of production
rules in order to generate
qualifying assertions for concept hypotheses.
 has been applied to some proposition
in the initial context.
The bold portions in the figures indicate
the terminological terms to be qualified, while the lighter ones depict
the qualifying instance.
A detailed example of the working of these rules will be provided in
the next section. A formal description of the rules is given in
hahn-et-al96a.
has been applied to some proposition
in the initial context.
The bold portions in the figures indicate
the terminological terms to be qualified, while the lighter ones depict
the qualifying instance.
A detailed example of the working of these rules will be provided in
the next section. A formal description of the rules is given in
hahn-et-al96a.














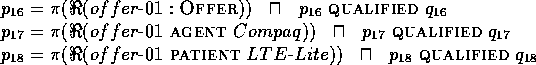


 PRODUCES
PRODUCES  is already true
is already true  .
.
 1 and
H
1 and
H 2, are
assigned the
syntactic quality label CASE-FRAME-ASSIGNMENT
(for the ease of readability, we will defer the consideration of
syntactic quality labels in the formal descriptions of the
current example until they contribute
to the discrimination between different hypotheses in later stages of the
sample analysis).
2, are
assigned the
syntactic quality label CASE-FRAME-ASSIGNMENT
(for the ease of readability, we will defer the consideration of
syntactic quality labels in the formal descriptions of the
current example until they contribute
to the discrimination between different hypotheses in later stages of the
sample analysis).
 (together with
(together with  ) triggers the generation
of two quality labels ADDITIONAL-ROLE-FILLER
according to rule III from the previous section
(note that for both spaces the propositions
) triggers the generation
of two quality labels ADDITIONAL-ROLE-FILLER
according to rule III from the previous section
(note that for both spaces the propositions  to
to  are assumed to hold).
are assumed to hold).
 ,
,  and
and  cause the verb
interpretation rule for OFFER to fire
yielding
cause the verb
interpretation rule for OFFER to fire
yielding  . Applying the terminological
axioms for OFFER leads to the deduction of
. Applying the terminological
axioms for OFFER leads to the deduction of  (the AGENT role of
OFFER restricts any of its fillers to
PRODUCER and its taxonomic superconcepts, viz. COMPANY
(
(the AGENT role of
OFFER restricts any of its fillers to
PRODUCER and its taxonomic superconcepts, viz. COMPANY
( ) and
PHYSICAL-OBJECT (
) and
PHYSICAL-OBJECT ( ), by way of
transitive closure).
In particular, H
), by way of
transitive closure).
In particular, H 1,
which covers
the AGENT interpretation contains the
following assertions (
1,
which covers
the AGENT interpretation contains the
following assertions ( to
to  ):
):

 2
(
2
( to
to  ) covers the PATIENT
interpretation:
) covers the PATIENT
interpretation:

 2 all hypotheses
generated
for Venturas (
2 all hypotheses
generated
for Venturas ( to
to  )
receive the quality label SUPPORTED, in H
)
receive the quality label SUPPORTED, in H 1 none.
This support (cf. rule II from the previous section) is
due to the conceptual proximity
1 none.
This support (cf. rule II from the previous section) is
due to the conceptual proximity  and
and
 have relative to
have relative to
 and
and  , respectively. Since both
hypothesis spaces, H1 and H2, imply that Venturas
is at least a PHYSICAL-OBJECT the label MULTIPLY-DEDUCED (rule IV)
is derived in the corresponding reified spaces, H
, respectively. Since both
hypothesis spaces, H1 and H2, imply that Venturas
is at least a PHYSICAL-OBJECT the label MULTIPLY-DEDUCED (rule IV)
is derived in the corresponding reified spaces, H 1
and H
1
and H 2. Rule III
also triggers in H
2. Rule III
also triggers in H 1
and
H
1
and
H 2, so it does not
contribute
to any further discrimination.
2, so it does not
contribute
to any further discrimination. 2, however,
can further be refined. According to the
terminological axioms, Compaq -- a
NOTEBOOK-PRODUCER (
2, however,
can further be refined. According to the
terminological axioms, Compaq -- a
NOTEBOOK-PRODUCER (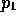 ) -- produces
NOTEBOOKs or ACCUs.
Thus, Venturas, the filler of the PRODUCES role of
Compaq (
) -- produces
NOTEBOOKs or ACCUs.
Thus, Venturas, the filler of the PRODUCES role of
Compaq ( ) must either be a
NOTEBOOK
( H
) must either be a
NOTEBOOK
( H 2
2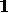 )
)
 2
2 )
)
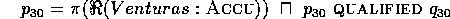
 2
2 (but not
H
(but not
H 2
2 ) is supported by
) is supported by
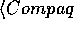 PRODUCES
PRODUCES 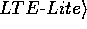 ,
,
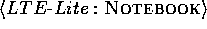 and
and
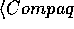 PRODUCES
PRODUCES 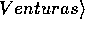 .
.
 1
and
H
1
and
H 2 the following
reified propositions hold:
2 the following
reified propositions hold:
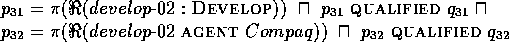
 1:
1:

 and H2
and H2 , Venturas may only fill
the PATIENT role. Given the occurrences of
, Venturas may only fill
the PATIENT role. Given the occurrences of  ,
,  and
and  , the verb interpretation
rule for DEVELOP fires and produces
, the verb interpretation
rule for DEVELOP fires and produces  .
This immediately
leads to the generation of a CROSS-SUPPORTED label (rule I from
the previous section) relative to proposition (
.
This immediately
leads to the generation of a CROSS-SUPPORTED label (rule I from
the previous section) relative to proposition ( ):
):

 (ACCU hypothesis)
leading to the generation of the (entirely negative) quality label
INCONSISTENT-HYPO in H
(ACCU hypothesis)
leading to the generation of the (entirely negative) quality label
INCONSISTENT-HYPO in H 2
2 .
The inconsistency is due to the fact that an accumulator cannot be part of
another accumulator.
For the hypothesis space H
.
The inconsistency is due to the fact that an accumulator cannot be part of
another accumulator.
For the hypothesis space H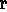 1 we get
1 we get
 2 we derive
2 we derive

 from hypothesis space H
from hypothesis space H 2
2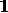 .
.
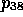 . Note that the
referent of "der Notebook
Venturas" ( the notebook from Venturas) has been resolved to
. Note that the
referent of "der Notebook
Venturas" ( the notebook from Venturas) has been resolved to
 by the anaphor
resolution component of our parser (strube95
strube95). This reference
resolution process is legitimated by hypothesis
by the anaphor
resolution component of our parser (strube95
strube95). This reference
resolution process is legitimated by hypothesis  of H
of H 1,
viz. (Venturas PRODUCES
1,
viz. (Venturas PRODUCES 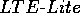 ). Thus,
we get for H
). Thus,
we get for H 1:
1:
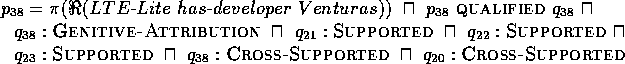
 over H1,
since the label APPOSITION-ASSIGNMENT
(from H
over H1,
since the label APPOSITION-ASSIGNMENT
(from H 2
2 ) is stronger than the label
GENITIVE-ATTRIBUTION (from H
) is stronger than the label
GENITIVE-ATTRIBUTION (from H 1),
all other labels being equal.
1),
all other labels being equal.
 (covering the NOTEBOOK
reading for Venturas)
whose reified counterpart holds 10 positive labels: MULTIPLY-DEDUCED (1),
SUPPORTED (8), CROSS-SUPPORTED (1),
(covering the NOTEBOOK
reading for Venturas)
whose reified counterpart holds 10 positive labels: MULTIPLY-DEDUCED (1),
SUPPORTED (8), CROSS-SUPPORTED (1), is ruled out,
since an inconsistency has been detected by the classifier. Finally,
H
is ruled out,
since an inconsistency has been detected by the classifier. Finally,
H 1
(holding the PRODUCER interpretation for Venturas) has
received a weaker level of confirmation ---
MULTIPLY-DEDUCED (1), SUPPORTED (3),
CROSS-SUPPORTED (1), and ADDITIONAL-ROLE-FILLER (2) --- and H1 is,
therefore, less
plausible than H2
1
(holding the PRODUCER interpretation for Venturas) has
received a weaker level of confirmation ---
MULTIPLY-DEDUCED (1), SUPPORTED (3),
CROSS-SUPPORTED (1), and ADDITIONAL-ROLE-FILLER (2) --- and H1 is,
therefore, less
plausible than H2 (cf. also the "Ranked Prediction Criterion" in Section "Quality-Based
Reasoning with Qualification Rules").
Summarizing our sample analysis, we, finally,
have strong indications for choosing
hypothesis H2
(cf. also the "Ranked Prediction Criterion" in Section "Quality-Based
Reasoning with Qualification Rules").
Summarizing our sample analysis, we, finally,
have strong indications for choosing
hypothesis H2 over H1
based on conceptual and
syntactic assessment criteria, since they both point into the same
direction
(which, of course, needs not always be the case).
over H1
based on conceptual and
syntactic assessment criteria, since they both point into the same
direction
(which, of course, needs not always be the case).