Dept. of Artifical Intelligence,
School of Computer Science and Engineering,
The University of New South Wales, Sydney, Australia, 2052
timm@cse.unsw.edu.au;
http://www.cse.unsw.edu.au/ 
timm
Tim Menzies
timm@cse.unsw.edu.au;
Dept. of Artifical Intelligence,
School of Computer Science and Engineering,
The University of New South Wales,
Sydney, Australia, 2052
http://www.cse.unsw.edu.au/ timm
September 30, 1996
Situated cognition (SC) claims that knowledge is mostly context-dependent and that symbolic descriptions elicited prior to direct experience are less important than functional units developed via direct experience with the current problem. If this were true, then we would need to modify the knowledge modeling approaches of KA which assume that re-using old symbolic descriptions are a productivity tool for new applications. There are numerous tools which, if added to conventional knowledge modeling, could be said to handle SC (e.g. machine learning, abduction, verification & validation tools, repertory grids, certain frameworks for decision support systems, expert critiquing systems, and ripple-down-rules). However, we require an experiment to assess the effectiveness of these tools as a response to SC.
"What is wanted is not the will to believe, but the will to find out,
which is the exact opposite."
- Bertrand Russell
"Measure what is measurable, and make measurable
what is not so."
- Galileo
Proponents of situated cognition (SC) in the AI field (e.g. [108, 109, 19, 22, 23, 3, 4, 117, 28, 7, 61]) assert that symbolic descriptions elicited prior to direct experience are less important than functional units developed via direct experience with the current problem (§3). More precisely, they argue that:
SC is hence a challenge to knowledge acquisition strategies that rely of the reuse of old symbolic descriptions (e.g. problem solving methods (PSMs) or ontologies) when building new applications (§2). There are numerous potential responses to the challenge of the SC including ignoring it (§4.1), verification & validation tools (§4.2), repertory grids (§4.3), expert critiquing systems (§4.4), machine learning (§4.5), certain frameworks for decision support systems (§4.6), and ripple-down-rules (§4.7)). However, we cannot assess the effectiveness of these potential responses since the few ``experiments'' in the KA field are poorly controlled (§3.4). A new experiment is therefore proposed which can assess the utility of these various responses (§5.2).
This section is a brief review of knowledge modeling. For more information, see the Related Work section of [116] and [64]. See also the ontology literature (e.g. [45]) which assumes that declarative descriptions of portions of old expert systems are useful for building new applications.
In Newell's KL approach, intelligence is modeled as a search for appropriate operators that convert some current state to a goal state. Domain-specific knowledge as used to select the operators according to the principle of rationality; i.e. an intelligent agent will select an operator which its knowledge tells it will lead the achievement of some of its goals. When implemented, this KL is built on top of a symbol-level containing data structures, algorithms, etc. However, to a KL agent, these sub-cognitive symbol-level constructs are the tools used ``sub-consciously'' as it performs its KL processing [75].
Newell's subsequent exploration of the KL lead to a general rule-based language called SOAR [92] which was the basis for the problem-space computational model (PSCM) [118]. Programming SOAR using the PSCM involves the consideration of multiple, nested problem spaces. Whenever a ``don't know what to do'' state is reached, a new problem space is forked to solve that problem. Newell concluded that the PSCM was the bridge between SOAR and true KL modeling [78, 76].
There is a difference between PSCM (hereafter, 
) and 
, a
KL-modeling variant which groups together a set of authors who argue
for basically the same technique; i.e. Clancey's model construction
operators [25], Steels' components of
expertise [105], Chandrasekaran's task analysis, SPARK/
BURN/ FIREFIGHTER (SBF) [60] and KADS [116]. The
fundamental premise of is that a knowledge base should be divided
into domain-specific facts and domain-independent PSMs.
In terms of this paper, the key difference between and is
how much architecture they impose on a solution: imposes more than
. PSMs are only implicit in . The
observation that a PSCM system is performing (e.g.) classification is
a user-interpretation of a lower-level inference (operator selection
over a problem space traversal) [118]. In ,
PSMs specify the data structures required for each
method. In , once a PSM is initially specified, it is assumed to
be set in stone for the life of the project.
It will be argue below that an SC-aware KA tool must minimise the
its architectural assumptions.
Further, whatever is built within those architectural assumptions must
be customisable.
One basis issue with is that extensive
customisation is not supported, particularly of the PSM. Our preferred
response to SC includes a PSM customisation tool (§5.1).
Dreyfus argues that the context-dependent nature of human knowledge makes it fundamentally impossible to reproduce in symbolic descriptions [36]. Searle takes a similar stand, claiming that the only device that can replicate human intelligence is another human [95, 96, 94] since only humans can share the same context. Birnbaum stresses ``the role of a concrete case in reasoning'' [7, p58,] and how logical AI cannot correctly handle such specifics, particularly when we have a specific conflicting belief.
Relativity, Heisenburg's uncertainty principle, the indeterminacy of quantum mechanics and Gödel's theorem demonstrate hard limits to the complete expression of truth. Many twentieth century thinkers have therefore adopted a relativist knowledge position. Kuhn notes that data is not interpreted neutrally, but (in the usual case) processed in terms of some dominant intellectual paradigm [50]. Popper [87] argues that, ultimately, we cannot prove the ``truth'' of anything since ``proofs'' must terminate on premises. If we request proofs of premises, then we potentially recurse forever. Hence, on purely pragmatic grounds, people are forced into an acceptance of certain premises. Note that the chosen premises may radically influence the conclusions reached. Agnew, Ford & Hayes offer their summary of contemporary thinking in the history, philosophy and sociology of science as:
Expert-knowledge is comprised of context-dependent, personally constructed, highly functional but fallible abstractions [2].
Easterbrook [38] argues that it is undesirable to demand that knowledge bases are consistent.
This insistence that expertise must be consistent and rational imposes restrictions of the knowledge acquired. The knowledge acquisition process becomes not so much the modeling of the expert's behaviour, but the synthesis of a domain model which need not resemble any mental model used by the expert [38, p264,].
The experience with expert systems is that the process of building consensus between individuals or creating an explicit record of it in a knowledge base introduces biases/errors. Silverman cautions that systematic biases in expert preferences may result in incorrect/incomplete knowledge bases (§4.4). Preece & Shinghal [89] document five fielded expert systems that contain numerous logical anomalies (see Figure 1). These expert systems still work, apparently because in the context of their day-to-day use, the anomalous logic is never exercised.
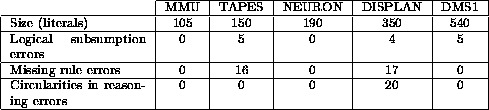
Figure: Samples of Errors in Fielded Expert Systems.
From [89].
Shaw reports an experiment where a group of geological experts built
models for the same domain, then reviewed each other's KBs as well as
their own twelve weeks later [98]. Note the two context
changes: from expert to expert and also a change of twelve weeks. For
the twelve week self-review study, it was found that an expert's
understandability and agreement with their own knowledge was less than
total (see Figure 2.A). For example, expert 
only
understands three-fifths of her own thinking three months ago. For
the cross-expert review, it was found that experts disagree
significantly with each other (see Figure 2.B). In this
cross-review study, it was found that levels of understanding may be
low (e.g. expert only understands expert 
's knowledge base
31.2% of the time). Levels of agreement were found to be even lower.
For example, expert only agreed with expert 's knowledge
base 8.3% of the time.
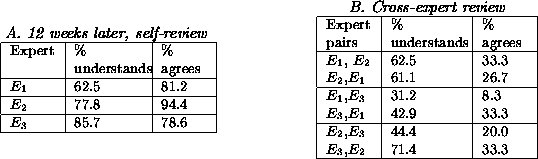
Figure: The Shaw study [98].
The Shaw study suggests that building a knowledge base representing
consensus knowledge can be difficult. There is evidence for this
elsewhere.
For example, between the various camps of
researchers, there is little agreement on the internal
details. Contrast the list of ``reusable'' problem solving methods
from KADS [116] and SBF [60] (termed ``knowledge
sources' and ``mechanism'' respectively). While there is some overlap,
the lists are different. Also, the number and nature of the problem
solving methods is not fixed. Often when a domain is analysed using
, a new problem solving method is
required [56]. Further, different interpretations exist
of the same problem solving method. For example:
Knowledge developed in one context may not be usefully reusable in another. Corbridge et. al. report a study in which subjects had to extract knowledge from an expert dialogue using a variety of abstract pattern tools [30]. In that study, subjects were supplied with transcripts of a doctor interviewing a patient. From the transcripts, it was possible to extract 20 respiratory disorders and a total of 304 ``knowledge fragments'' (e.g. identification of routine tests, non-routine tests, relevant parameters, or complaints). Subjects were also supplied with one of three problem solving methods representing models of the diagnostic domain. Each model began with the line ``To help you with the task of editing the transcript, here is a model describing a way of classifying knowledge''. Model one was an ``epistemological model'' that divided knowledge into various control levels of the diagnosis process. Model one was the ``straw man''; it was such a vague description of how to do analysis that it should have proved useless. Model two was a KADS problem solving method for diagnosis. Model three was ``no model''; i.e. no guidance was given to subjects as to how to structure their model. The results are shown in Figure 3. The statistical analysis performed by Corbridge et. al. found a significant difference between the performance of groups 3 compared to groups 1 and 2. Further, no significant difference could be found between the group using the poor problem solving method (model 1) and the group that using a very mature problem solving method (model 2). That is, sophisticated and mature descriptions of previously used knowledge (i.e. the KADS diagnosis description) were not found to be a productivity tool.
Figure: Analysis via different models in the Corbridge
study [30].
While human beings have found it useful to use symbolic descriptions when co-ordinating their activities, it is not necessarily true that those symbolic descriptions are used internally by a single human in their own reasoning processes. Clancey [19, 22] and Winograd & Flores [117] argue that it is a mistake to confuse the symbolic descriptions which humans use to co-ordinate their activities and reflect about their actions (i.e. language) with how humans might generate their minute-to-minute behaviour. That is, we should not confuse our conversations about our thoughts with the actual content of those thoughts.
The Winograd & Flores line is that computers are not modeling tools per se but are really communication tools that facilitate the mediation of the exchange of ideas. Similarly, Clancey rejects the view that human inference is best replicated as matching/retrieving. Rather, says Clancey, these structures are created on-the-fly as posthoc symbolic justifications of a process which is not symbolic:
The neural structures and processes that coordinate perception and action are created during activity, not retrieved and rotely applied, merely reconstructed, or calculated via stored rules and pattern descriptions [23, p94,].
Clancey's view is not resolved merely by declaring that knowledge representations are approximate surrogate models of reality (e.g. as proposed by [33]). Rather, Clancey believes that symbolic structures are not only approximations of human knowledge but also that human knowledge changes as a result of applying it.
Every action is an interpretation of the current situation, based on the entire history of our interactions. On some sense every action is automatically an inductive, adjusted process [19, p238,].
Researchers into decision support tools make a case something like weak SC. They argue that human ``knowledge'' appears in some social context and that context can effect the generated ``knowledge''. Phillips [83] and Bradshaw et. al. [9] characterise model construction as a communal process that generates symbolic descriptions that explicate a community's understand of a problem. If the community changes then the explicit record of the communities shared understanding also changes; i.e. ``truth'' is socially constructed. Such an explicit expression of current beliefs may prompt further investigation and model revision; i.e. writing down models of ``truths'' can cause ``truth'' to change. Decision support tools are discussed later (§4.6).
Suchman [108, 109, 3] argues that real-world planning systems have to model their environment as well as their own goals. For example, a photocopier advisor system must...
...focus on the ways in which the photocopier and its user work together to maintain a shared understanding of what is going on between the tow of them and the copier...Far from executing a fully operational plan for effecting a fixed goal, the photocopier users continually reinterpreted their situation and based their various actions on their evolving interpretations [3].
If weak SC was false, then we should see that using knowledge does not change that knowledge; i.e. knowledge maintenance for static domains should terminate when it arrives at ``truth''. Compton [27] reports studies that documented the changes made to models of biochemistry diagnosis systems. The Garvan ES-1, expert system was developed using a traditional iterative prototyping knowledge engineering methodology. Rules that began as simple modular chunks of knowledge evolved into very complicated and confusing knowledge (e.g. Figure 4). Note that this system was developed in a static domain; i.e. the system was a post-processor to a biochemical assay unit that did not change for the lifetime of the project. Despite this, the Garvan ES-1 expert system never reached a logical termination point, despite years of maintenance. There was always one more major insight into the domain, one more major conceptual error, and one more significant addition [27]. A graph of the size of that knowledge base versus time (Figure 5) is consistent with either a linear growth curve or a logarithmic curve. Note that a linear curve would support the SC premise, while a logarithmic growth which would falsify weak SC since that would suggest that the KB is approaching ``the truth''. However, even if this was true for Garvan ES-1, note that the asymptote is very slow (see the Logarithmic fit of Figure 5). Even if we can approach ``the truth'', it seems it may take years to do so.
Figure: A rule maintained for 3 years. From [27].
Garvan ES-1 was decommissioned before enough data could be collected
to test if the growth curve was linear or logarithmic.
Compton is monitoring the maintenance of PIERS [90], a
much larger system (which is version 2 of the above diagnosis system
). A 
growth in KB size has been noted in that
system. Significantly, the user-group sponsoring the project have
created a permanent line item in their budget for maintenance. They
anticipate that routinely every day, an expert will review the
generated diagnoses and change some of the KB. That is, they believe
that the model will never be finished/correct [26].
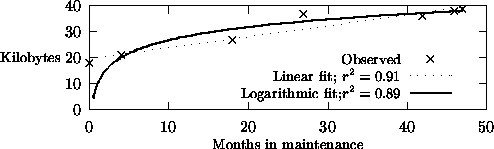
Figure 5: Garvan ES-1 knowledge base size
Experiments in machine learning endorse the proposition that any version of a model can be improved after more experience. Machine learning programs input training data to generate a model. Catlett's research [16] explored the following area. Given a large amount of training data, is it necessary to use it all? That is, after a certain number of examples, is further experience (i.e. training data) superfluous? To test this, Catlett used C4.5 [91] to generate 20 decision trees for eleven machine learning problems using either (i) all the training cases or (ii) half the cases (randomly selected). Each generated tree was assessed using the test cases. In all cases, Catlett found that a statistically more accurate model could be generated using all the training data, rather than some randomly chosen subset (Figure 6). Note that while the theory learnt from N cases may be only marginally better than the theory learnt from N/2 cases (average reduction in error = 0.97%), the size of the better theory is 30% to 90% bigger (average increase in tree size = 53%); i.e. more examples prompted a significant reorganisation of the model (exception: the demon domain). That is, we may never know enough to create the correct model and that experience can significantly and continually modify old symbolic descriptions of knowledge.
§3.1 endorsed the SC premise and §3.2
endorsed weak SC. However, this endorsement does not
necessarily imply an endorsement of strong SC. Like Vera
& Simon in §4.1.3, this paper argues
that symbolic systems are
still a useful paradigm. It is not necessarily true what (e.g.)
Birnbaum [7] and McDermott [61] argue;
i.e. that the
obvious alternative to logical AI is some type of
procedural/functional semantics (i.e. strong SC).
McDermott's
motivation for a move away from symbols is based on his view that
there has been ``skimpy results so far and ...it is going to be
very difficult to do much better in the
future'' [61, p151,]. Coming from McDermott,
this is a telling criticism since, prior to this article, he was one
of the leading proponents of that logical school [17].
With the benefit of a little historical hindsight, we can defeat some of McDermott's 1987 arguments. McDermott repeatedly uses Forbus' 1984 Qualitative Process Theory (QPT) [42] as an worthy example of an algorithmic/non-logical system. McDermott originally demanded in 1984 that Forbus record the logical axioms underlying QPT. However, in 1987, McDermott comments that ``...the task, seemingly so feasible (is) actually impossible'' [61, p152,]. Note that, 12 years later, QPT was later implemented via a compilation into QSIM [32]. QSIM was a special-purpose theorem-prover built by Kuipers in 1986 for processing qualitative differential equations [51]. In 1993, Kuipers [52, p134,] acknowledged is a textbook application of Mackworth's constraint-logic system [58, 57]. That is, QPT was an instantiation of a logic-based system. However, when it was first developed, this was not known.
The lesson of the QPT story is that logical/symbolic descriptions could handle seemingly functional semantics. Descriptive symbolic systems that could be said to handle weak SC without requiring strong SC are described below (§4).
There are two outstanding experimental studies that challenge the SC
case that knowledge is context dependent. Runkel reports large
amounts of verbatim reuse using a toolkit of problem solving
strategies that separated search control from other domain
knowledge [93]. Marques et. al. report significantly reduced
development times for expert systems using the 13 mechanisms in the
SBF toolkit (eliminate, schedule, present, monitor, transform-01,
transform-02, compare-01, compare-02, translate-01, translate-02,
classify, select, dialog-mgr). In the nine applications studied by
Marques et. al., development times changed from one to 17 days (using
SBF) to 63 to 250 days (without using SBF) [60]. To the
best of our knowledge, these two studies represent the current
high-water marks in software reuse in both the conventional software
engineering and knowledge engineering
paradigms.
Nevertheless, neither experiment is a convincing demonstration of general knowledge reuse. The Runkel experiment had poor control of the resources used while the SBF experiment had poor control of the product produced. All the applications studied in ththe author's internal (possibly non-symbolic) model informed the usage of the tools. Also, Runkel does not report the time required to use his approach; i.e. the Runkel study cannot be used to depend the proposition that reusing old symbolic descriptions is a productivity tool for new applications.
One response to SC is to argue that current techniques work, so why do we need to change them? This paper discounts this argument (§4.1) and move on to techniques that address weak SC. Weak SC suggests that generating a explicit record of a specification is less of an issue than changing that specification over time. Therefore, any technique which can support specification change is a potential response to SC; e.g. verification & validation tools (§4.2), repertory grids (§4.3), expert critiquing systems (§4.4), machine learning (§4.5), certain frameworks for decision support systems (§4.6), and ripple-down-rules (§4.7). Note that:
Clancey cautions [20] that we should not confuse pragmatic discussions about techniques for knowledge acquisition (e.g. [18, 21, 25]) with discussions about the basic nature of human intelligence (e.g. [19, 22, 23]). Clancey prefers to reserve discussions on SC for the creation of human-equivalent robots which react to real-world situations since, he says,
SC argues that human activity is not strictly mediated by inference over descriptions nor is activity a compiled result of such inference [24].
Clancey's remarks notwithstanding, this paper argues
that SC has a
significant impact on KA.
If weak SC is true, then
we cannot expect to reuse
old symbolic descriptions of ontologies or PSMs
as a productivity tool for some current application.
Instead of focusing on reusing old knowledge, KA
SC-style should focus on how we build and change models. That is,
expertise is not a function of using a large library of old knowledge
as argued in [53] and favoured by the
approach. Rather, expertise is the ability to quickly adapt old
models to new situations.
A KA methodology that acknowledges SC must offer details about creating and changing a knowledge base. A review of the KA literature suggests that most of the effort is in knowledge analysis and not knowledge maintenance (exceptions: [34, 27]). Current KA practice has not acknowledged SC since, if it did, there would be more work in knowledge maintenance.
It could be argued that the evidence for weak SC is not convincing. For example, a reviewer of this paper wrote:
Discussion of the pilot study done by Corbridge (§3.1) involves results are too premature to bolster the SC claim. Discussion of one PSMs in SBF and KADS (§3.4) also seems less than convincing evidence for the SC claim.
This comment is true:
the evidence above is not convincing. However, at the very
least, the above evidence is suggestive
that we need to make a careful review of the
perceived successes of current KA approaches.
Given the current lack of good experimental evidence demonstrating the
utility of (§3.4), we need to do more experiments (§5.2).
Proponents of may argue that they have no case to
answer. By some measures, is a successful
paradigm. For example, Wielinga et. al. report that, as of 1992,
KADS has been used in some 40-to 50 KBS projects, 17 of which are
described in published papers [116]. Further, if the
situation is as bad as suggested above, then how is it that we have so
many seemingly successful expert systems (e.g. MYCIN [119],
CASNET [115], PROSPECTOR [15, 37],
XCON [5], VT [59], PIGE [69])?
This kind of argument is the basis
of Vera & Simon's criticisms of SC [113, 112, 114].
They describe as
``preposterous'' [112, p95,] a claim by Agre that ``nobody has
described a system capable of intelligent action at all- and that
nothing of the sort is going to happen soon'' [4, p69,]. We
suspect that they would also object to McDermott's lament about
``skimpy results so far'' (§3.3). Vera & Simon argue that
the physical symbol system hypothesis (PSSH) [77] has been a
fruitful paradigm which can reproduce many known behaviours of
experts. They decline to reject PSSH for strong SC since, if
they adopted, e.g. Clancey's situated paradigm [23], then
they are unclear on what predictions can be made and what experiments
can be performed. That is, they argue that SC is unfalsifiable and
unscientific.
Nevertheless,
it would be a mistake for proponents of to
use the Vera & Simon arguments as support for their reuse
paradigm. Vera & Simon are only arguing against strong SC (which
they call ``situated action''). A
symbolic system that can implement weak SC would still satisfy
Vera & Simon's broad definition of a symbolic system while
challenging the paradigm.
Further, just because a system based on explicit symbolic descriptions works, this says nothing about the best way to build and maintain those symbolic descriptions. Clancey acknowledges the role of symbolic descriptions in working systems [19, p278,][25]. Symbolic descriptions, Clancey argues, are useful to planning about the future and reflecting on action rather than immediately reacting to a new situation.
Human reasoning is immensely more successful by our ability to simulate what might happen, to visualize possible outcomes and prepare for them. We do this by reflecting, saying what we expect, and responding to what we say [19, p247,].
However, Clancey's symbolic descriptions are not as fixed as those in Ontolingua [45] or the inference layer of KADS.
It remains to explain how (the symbolic descriptions) develop.... Most learning programs grammatically describe how representations accumulate within a fixed language. They don't explain how representations are created, or more generally, the evolution of new routines not described by the given grammar [22, p279,].
Knowledge acquisition is the key point that is ignored by Vera & Simon. They comment on the successes of working symbolic descriptions of human knowledge, not on the effort involved in constructing those descriptions. Despite careful attempts to generalise principles of knowledge acquisition, (e.g. [107]), expert systems construction remained a somewhat hit-and-miss process. By the end of the 1980s, it was recognised that our design concepts for knowledge-based systems were incomplete [13]. For example, Steels [106] cites an example where an expert could not solve a problem over the phone but, as soon as they walked into the room where the trouble was, could solve it instantly. Examples like this encourage the knowledge-relativists within KA to argue that we have under-valued the role of context in the creation of our symbolic descriptions.
Weak SC suggests that a specification considered correct at time
may become potentially incorrect at 
. It has been
argued
previously [62] that such potentially inaccurate models must
be tested, lest they generate inappropriate output for certain
circumstances. Testing can only demonstrate the presence of bugs
(never their absence) and so must be repeated whenever new data is
available. That is, testing is an essential, on-going process
through-out the lifetime of a knowledge base.
Preece and Zlatereva describe test programs based on the logical
structure of rule-based expert systems. Preece's verification tools
detect anomalies in those structures [88] while
Zlatereva's validation tools analyse that structure to generate a test
suite which will exercise all parts of the
rule-base [121].
Verification tools search for syntactic anomalies within a knowledge
base such as tautologies, redundancies, and circularities in the
dependency graph of literals in a knowledge base [89].
Many of Preece's verification tools can be mapped into a
graph-theoretic analysis of the dependency graph 
of literals in
a KB used in HT4 (e.g. Figure 7.A).
For example, a test for ``unreachable conclusions'' can be
converted into the following graph-theoretic process. Compute the
components (separate sub-graphs) of . If a component contains
conclusions but no system inputs, then those conclusions are
unreachable. Also, a test for ``circularities'' can be converted into
a computation of the transitive closure of . ``Looping'' means
finding a literal in its own transitive closure. Verification is not
a definitive test for a KBS. Preece reports example where working
expert systems contained syntactic anomalies, yet still performed
adequately (recall Figure 1).
Validation tools assess knowledge via some external semantic criteria; e.g. testing that a knowledge base model of X can reproduce known behaviour of X. If such a test suite of behaviour is missing, then non-monotonic reasoning techniques can be used to explore the dependency graph between KB literals to find sets of input literals which will exercise the entire knowledge [44, 120]. However, an expert still has to decide what output is appropriate for each generated input. This can introduce a circularity in the testing procedure. After an expert describes their world-view in a model, that same expert will be a asked to specify the results of certain inputs. If the expert then uses the same model to predict the output, then they would be using a potentially faulty model to generate a potentially faulty prediction about the output.
Our preferred validation approach is for the input-output test pairs
to be generated totally separately to the current model; e.g. from
real-world observations of the entity being modeled in the KB. Based
on work by Feldman & Compton [41], a
general validation framework based on the HT4 abductive
inference engine has been developed.
Elsewhere [68], we have given an overview
of abductive
research [80, 14, 39, 97, 85, 68].
Here, we offer an approximate characterisation of abduction as the
search for consistent subsets of some background theory that are
relevant for achieving some goal. If multiple such subsets can be
generated, then a 
assessment operator selects the preferred
world(s). For example,
suppose HT4 wants to validate that certain
put goals can be reached from using the 
puts shown
in the dependency graph of Figure 7.A. In that
Figure, x 
y denotes that
y being up or down can be explained by x being
up or down respectively and
x 
y denotes that y being
up or down could be explained by x being down
or up respectively. HT4 can find the following proofs
connecting s to s: 
= 
, 
=
, 
= 
, 
= 
, 
=
.
A. A knowlege base
a ++> x ++> y ++> \
| ^ |
| + |
| + |
| |_________ d
| ^
| +
| +
\____c ++> g _____|____++>e
^ |
- |
- |
b____|__________--> f
B. Two generated worlds
World #1
aUp __> xUp __> yUp __> \
| |
| |
| |
| dUp
| ^
| |
| |
\____cUp __> gUp _______|______>eUp
bUp_______________> fDown
World #2
aUp __> xUp __> yUp __> \
|
|
|
dUp
cDown __> gDown ___
| |
| |
bUp______|____________--> f
Figure 7: Worlds generation
These proofs may contain assumptions, i.e. literals that
are not known . Continuing the example of
Figure 7.A, if = , then
{xUp,yUp,cUp, cDown, gUp, gDown} are assumptions. If we can't
believe that a variable can go up and down simultaneously,
then we can declare {cUp, cDown, gUp, gDown}
to be conflicting
(denoted ).
Figure 7.A shows us that
g is fully dependent
on c. Hence
the key conflicting assumptions are {cUp,
cDown} (denoted base controversial assumptions or ).
We can used to find consistent belief sets called worlds
. A proof is in if that proof does not
conflict with the environment (an environment is a
maximal consistent subset of ). In our example,
={cUp} and ={cDown}. Hence,
={ , , , } and
={ } (see
Figure 7.B).
Abductive validation is simply the application of the above algorithm
with a assessment operator that returns the world(s) with
the maximum cover; i.e. overlap with . The overlap of
and is {dUp,eUp,fDown} and the overlap
and is {dUp,fDown};
i.e. = 3 = 100% and = 2 = 67%.
The maximum cover is 100%; i.e. their exist a set of assumptions
({cUp}) which let us explain all of and this theory has
passed HT4-style validation. Note that this procedure
corresponds to answering the following question: ``how much of the
known behaviour of X can be reproduced by out model of X?''.
This abductive validation was applied to Smythe '89, a model of glucose regulation published in an international, refereed journal [103]. Using an earlier version of HT4 (which they called QMOD and we call HT1) Feldman & Compton reported that only 69% of the known observations could be explained by Smythe '89 [41]. In our re-work of that study, and-vertex processing and multiple causes processing was added, thus allowing the processing of more of the known observations. With those changes, HT4 found that only 55% of the observations were explicable [67]. When these errors were shown to Smythe, he found them novel and exciting [41]; i.e. the domain expert found that these errors were significant. This is both a disturbing and exciting finding. It is disturbing in the sense that if the very first large-scale medical theory analysed by HT4 contains significant numbers of errors, then it raises doubts as to the accuracy of theories in general (a result which would be consistent with the SC premise).
Gaines & Shaw explore techniques for resolving conflicts in terminology. The conceptual systems of different experts are explicated and compared using a technique called entity-attribute grid elicitation [43]. Experts are asked to identify dimensions along which items from the domain can be distinguished. The two extreme ends of these dimensions are recorded left and right of a grid. New items from the domain are categorised along these dimensions. This may elicit new dimensions of comparisons from the expert which will cause the grid to grow (see [99] for a sample of such grids). Once the dimensions stabilize, and a representative sample of items from the domain have been categorised, then the major distinctions and terminology of a domain has been defined. Differences between the conceptual views of different experts can be identified (e.g. their categorisations are different). Gaines & Shaw describe automatic tools for generating plots representing the proximity of different expert's conceptual systems [43].
Gaines & Shaw focuses on identifying and resolving conflicts in the meaning of individual terms, not on conflicts in the semantics of the models built using combinations of those terms. A model-level conflict detection facility such as abductive validation requires knowledge of how terms are combined.
Silverman [100, 101] advises that attached to an expert system should be an expert critiquing system which he defines as:
...programs that first cause their user to maximise the falsifiability of their statements and then proceed to check to see if errors exist. A good critic program doubts and traps its user into revealing his or her errors. It then attempts to help the user make the necessary repairs [101].
Silverman divides an expert critiquing system into (i) a deep model
which can generate behaviour; (ii) a differential analyser which
compares the generated behaviour with the expected behaviour; and
(iii) a dialogue generator that explains the errors and assists in
correcting them. Dialogue generators are very domain-specific.
Silverman's research seems to be aimed at an
implementation-independent analysis of the process of ``critiquing'' a
program; i.e. ``critiquing'' as an add-on
to existing systems, not as a built-in that is fundamental to the
whole KBs life cycle. While this approach is useful,
a more extensible approach would to change the structure of knowledge-
bases systems such that critiquing is built into the system
(see §5.1).
In the case
where the design of the system can be altered to integrate a testing
module, the abductive approach of HT4 is an
alternative approach to critiquing. Silverman's ``deep models'' are
the theory that generates the proofs (e.g. Figure 7.A) while
the difference analyser is the assessment operator which
reports what behaviours can't be covered.
Validation and verification techniques can only automatically find faults. Machine learning (ML) techniques can fully or partially automate the creation or the fixing of a specification. Given some input facts, some goals, and some prior knowledge, then ML can use induction, analogy, deduction, or heuristic techniques to generate a revision to the prior knowledge [72].
If numerous examples are available (say, hundreds to thousands), then empirical inductive techniques such as mathematical regression, genetic algorithms, neural nets or other techniques (e.g. nearest-neighbor algorithms, decision-tree generation, simple Bayesian reasoning [49]) can propose a new theory. These techniques have not come to replace standard knowledge acquisition for several reasons. Firstly, most naturally-occurring domains are data-poor. Automatic empirical inductive generalisation in such data-poor domains is an unreliable technique. Secondly, once a theory is revised, the revisions must be acceptable to a human reader. Empirical inductive generalisation techniques such as neural nets, genetic algorithms, or decision tree learners may generate a revision of prior knowledge that is too big or too awkward to read. Further, most empirical inductive generalisation machine learning algorithms (e.g. the C4.5 decision tree of Figure 6) make no attempt to preserve current beliefs (exception: inductive logic programming [74]). It may be unacceptable to permit a learning algorithm to scribble all over a knowledge base, particularly those portions which the user has some commitment to.
In domains that lack sufficient input facts for empirical inductive generalisation, then deductive ML algorithms exist which (i) build an explanatory structure across the current knowledge base then (ii) edit this structure to generate a refinement to the knowledge base. This can be done using automatic tools (e.g. explanation-based generalisation [111]) or semi-automatic tools where the user's opinions are used as part of the theory refinement loop. Heuristic KB refinement (e.g. KRUST [31, 81] and expert critiquing systems (§4.4)) are a kind of ``machine learning'' algorithm in which domain-specific principles are used to fault a KB and assist a human in fixing the faults.
Note that the new theory learnt by deductive ML algorithms can only ever be a subset of the prior knowledge over which explanatory structures can be build. For example, the worlds of Figure 7.B represent the consistent explanation structures we can generate from Figure 7.A. Each such set is just a subset of the edges in the dependency graph between the literals of Figure 7.A. If we cached these worlds, then we could say we have ``learnt'' that in the case of Figure 7.A, there are two possibilities depending on the value of c.
In domains that lack both sufficient input facts for empirical inductive generalisation and prior knowledge, then the only other way to build a theory is to ask an expert; i.e. standard knowledge acquisition. In decision support systems (§4.6), for example, developers are not recording a model of an existing domain. Rather, they are using software tools to build a model for a newly, poorly understood domain which has not been previously documented.
Workers in decision support systems deliberately try to model the context of the decision making process. DSS theory believes that management decision making is not inhibited by a lack of information. Rather, it is confused by an excess of irrelevant information [1]. Modern decision-support systems (DSS) aim to filter useless information to deliver relevant information (a subset of all information) to the manager. Simon originally characterised decision making as a three stage process: intelligence (scanning environment), design (develop alternative courses), and choice (selection of alternative) [102]. Our preferred definition of a decision-support system is based on Brookes [12]' who developed it from Simon's and Mintzberg's model [73]. The goal of a DSS is management comfort, i.e. a subjective impression that all problems are known and under control. More specifically, managers need to seek out problems, solve them, then install some monitoring routine to check that the fix works. A taxonomy of tasks used in that process is shown in Figure 8.
The Simon categories
Intelligence Design Choice
Comfort = 1 + 2 +3
1 = Finding Problems
1.1 Detection....................X
1.2 Diagnosis....................X
2 = Solving Problems
2.1 Alternative generation...................X
2.2 Alternative evaluation...................X
2.3 Alternative selection...........................X
3 = Resolution
3.1 Monitoring
Figure 8: Components of management comfort
Other DSS workers have a similar view. Boosse et. al. assume that once the group's mode is elicited, it will be subsequently exported into an executable form. Portions of the BBKS and the Brookes' models overlap. The BBKS system lets groups manipulate their group model, its inter-relationships, and the group's criteria for selecting the best alternative. BBKS stress that:
The process of generating and scoring alternatives are at the heart of most decision processes. [8]
That is, more important than representing and executing a model is an
ability to assess a model. Note that the operator of
HT4 directly implements this alternative generation,
assessment,
and selection procedure. Further, abduction can be used for other DSS
tasks such as diagnosis [29] and monitoring.
(§2) typically assumes that prior to
building a system, an extensive analysis stage develops a design for
the system.
Compton reports experiments with a completely reversed approach.
In
ripple-down-rules (RDR), there is no analysis period. Starting
with the
single rule ``if true then no classification'', KA in an RDR
system consists only of
fixing
faulty rules using
an unless patch attached at the end of a rule condition.
Patches are themselves rules which can be recursively patched. Experts
can never re-organise the tree; they can only continue to patch their
patches. If a new case motivates a new patch, that this case is
stored with the new patch. Compton argues that these
(RDR) trees models the context of knowledge
acquisition. When a case is processed by an RDR tree, its context is
the set of cases in the patches exercised by the new case. When
looking for new patches, experts can only choose from the
difference of the attributes in the current case and the attributes
exercised down to the current faulty rule.
RDR trees are a very low-level representation. Rules cannot assert
facts that other rules can use. In no way can a RDR tree be called a
model in anything like a sense. Yet this low-level
model-less approach has produced large working expert systems in
routine daily use. For example, the PIERS system at St. Vincent's
Hospital, Sydney, models 20% of human biochemistry sufficiently well
to make diagnoses that are 99% accurate [90]. RDR has
succeeded in domains where previous attempts, based on much
higher-level constructs, never made it out of the prototype
stage [82]. Further, while large expert systems are
notoriously hard to maintain [34], the no-model approach
of RDR has never encountered maintenance problems. System development
blends seamlessly with system maintenance since the only activity that
the RDR interface permits is patching faulty rules in the context of
the last error. For a 2000-rule RDR system, maintenance is very simple
(a total of a few minutes each day). Compton argues that his process
of ``patching in the context of error'' is a more
realistic KA approach than assuming that a human analyst will behave
in a perfectly rational way to create some initial correct
design [28].
Weak SC suggests that,
as far as possible, the
symbolic structures inside an expert system must be changeable. Any
representational system assumes certain primitives which can't be
changed. assumes that a PSM does not change over the lifetime of
a project. Hence, our preferred response to SC is a PSM-maintenance
environment called ripple-down-rationality, or RD-RA.
RD-RA is described below (§5.1). This description is only a preliminary sketch since it is new work-in-progress. We present it here in order to motivate our SC experiment (§5.2). If the reader disagrees with our proposal, we invite them to consider how they would assess the success or failure of RD-RA.
For reasons of generality, we base RD-RA around the HT4 abductive validation engine. Note that many common knowledge representations can be mapped into dependency graphs like Figure 7.A. For example, horn clauses can be viewed as a graph where the conjunction of sub-goals leads to the head goal. In the special (but common) case where the range of all variables is known (e.g. propositional rule bases), this graph can be converted into a ground form where each vertex is a literal. Invariants may be added to represent sets of literals that are mutually exclusive (e.g. cUp and cDown). Such graphs are commonly computed for the purposes of optimisation or verification (§4.2).
An interesting feature of abduction is that it both a validation and an inference engine. It maps exactly into Clancey's characterisation of expert systems as devices that build a system-specific model (SSM) or Breuker's component's of solutions [11, 25]. As evidence of this, we can express the details of a wide range of KBS tasks in this abductive framework; e.g. intelligent decision support systems (§4.6 & [63]), diagrammatic reasoning [70], single-user knowledge acquisition, and multiple-expert knowledge acquisition [65], certain interesting features of human cognition [66]. natural-language processing [79], design [84], visual pattern recognition [86], analogical reasoning [40], financial reasoning [46], machine learning [48], case-based reasoning [54], expert critiquing systems (§4.4), prediction, classification, explanation, tutoring, qualitative reasoning, planning, monitoring, set-covering diagnosis, consistency-based diagnosis, verification and validation (§4.2 & [68, 67]). Further, abduction handles certain hard and interesting cases; such as the processing of indeterminate, under-specified, globally inconsistent, poorly measured theories. Inferencing over such theories implies making assumptions and handling mutually exclusive assumptions in different worlds.
RD-RA is a combination of RDR with HT4 and a
graph-theoretic version of SOAR. Recall Newell's principle of
rationality (§2): part of intelligence is the appropriate
selection of operators to decide between possible inferences.
HT4's operator's can be characterised by how much
information they require to execute. A node-level operator could
assess the utility of using some edge based on some numeric weight on
that edge. A proof-level operator could assess the utility of
using some edge based on its contribution to a growing proof and how
that growing proof compares to other known proofs (e.g. like in beam
search). A worlds-level operator could assess the utility of a
world based on various criteria (e.g. the validation
in §4.2).
In RD-RA, a PSM is implemented as sets of operators.
If we use RDR rules to control the modifications of the
different levels of operators then, potentially,
we a maintenance
environments for PSMs. Recall that each
operator is a small procedure that classifies each proposed inference
(edge, world) as ``acceptable'' or ``cull''. A little RDR KB
could maintain each operator.
Consider a KB comprising a state space connecting literals and a PSM which controls the traversal of that state space. Weak SC has no impact of KA and RD-RA is unnecessary if, in the usual case, the edges and the PSM do not change radically after some initial analysis period.
Let us characterise two opposing KA processes:
put, put pairs.
operators would not be added till after the
system has processed put, put pairs
(recall that
in RD-RA, a PSM is implemented as
sets of operators).
Note that if we add modification dates to all edges, PSMs,
and put, put pairs then we can auto-detect if a
software
artifact is generated via MIP or AIP.
Both MIP and AIP contribute edges to a knowledge base dependency graph. This knowledge base is subsequently evaluated via our validation process (§4.2). We would declare MIP or AIP to be satisfactory if it can generate competent systems from the same specification (e.g. one of the Sisyphus projects [55]). Note that we can assess competence via the HT4 abductive validation algorithm.
Our validation process also lets us identify good
edges (§4.2). Further, we can declare a operator to
be good if it was exercised in the generation of good
edges. We would declare either the MIP or AIP process superior
if it produced more good edges/operators sooner than the other.
We would declare weak SC irrelevant to the practice of KA if curves of ``number of good edges changed'' vs ``months in production'' or ``revisions to good operators'' vs ``months in production'' (e.g. a variant on Figure 5) flatten out very quickly. We can also falsify the SC premise if AIP KA is superior to MIP KA when both are applied to the same application.
Note that the above process has to be repeated a number of times over similar applications developed by skilled programmers who know their tools; i.e. such as in the Sisyphus experiments.
Existing KA methods, including , can deliver
successful applications (§4.1.3). However, which is the
best method? The crucial test for a particular KA technique is not
whether or not it can deliver applications. Rather, it should be
``can method X deliver applications better than the alternatives?''.
In this paper two alternative approaches to KA have been characterised: (i) analysis-intensive processing (the dominant view) and (ii) maintenance intensive processing (a minority view). It has been argued that there is enough evidence for weak SC to motivate a review of analysis intensive processing. Current experimental evidence is not sufficient to inform such a review. Hence, several potential responses to the challenge of SC have been discussed and a experiment that could determine the impact (if any) of weak SC on KA has been proposed.
In order for this test to be fair to the current
paradigm, we will need to build a set of translators that convert the
constructs found in current KBS and information systems
methodologies down into structures
like the HT4 graphs. The implementation of a library of such
translators is our current TROJAN project.
This paper has benefited from the careful comments of Bill Clancey, Paul Compton, John O'Neill, and the anonymous referees.
Some of the Menzies papers can be found at
http:// www.cse.unsw.edu.au/ timm/pub/
docs/papersonly.html.
Assessing Responses to Situated Cognition
This document was generated using the LaTeX2HTML translator Version 96.1-e (April 9, 1996) Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 0 words.
The translation was initiated by Tim Menzies on Mon Sep 30 16:14:28 EST 1996
timm timm/pub/
docs/papersonly.html