We have to propose a method with definitions for each of the six components.
The goal that guides the choice for the Cover
and NotContra components is
explanation-notion(standard), since the system contains knowledge that
standard entailment is most frequently used in diagnostic methods
(as opposed to the use
of non-standard variatons of entailment proposed in [ten Teije & van Harmelen, 1996a]). As a
result, we choose for both explanation relations ( Cover and
NotContra) the
classical entailment relations (
and
respectively). The
other four components are chosen blindly.
The proposed method is
:
In Table 7 the definitions of the components are briefly described. In [ten Teije & van Harmelen, 1994] the definitions of some of these components are given more formally.
Figure 7: The components of the proposed method.
The dynamic goals now become all the goals that have not already been statically determined. In this case the only dynamic goal is max-number-diagnoses(2).
Knowledge-verification
One of the usual constraints on diagnostic methods is to demand that the Cover component is at least as strong as the NotContra component. After all, if an observable is entailed by a consistent theory, then that observable is also consistent with this theory.
The method described by term (3) does not violate this constraint. However, there is another assumption conflict, because #-min assumes that every cause has equal likelyhood. This means that the knowledge-verification step has failed, and therefore a new propose step is started.
Propose
We now propose another method. Because this step is still guided by
the same static
goal as before ( explanation-notion(standard)), the method still
contains
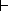as Cover definition and 
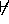as NotContra definition.
The other components are again chosen blindly.
The propose method is now:
Knowledge-verification
As in ``
knowledge-verification'' there
is no violation of
the constraint concering the Cover and NotContra components.
The other assumption-confllict also disappears because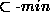 
does not assume equal likelyhood of causes. As a result,
in this case assumptions conflicts no longer occur.
Simulation-Verify
In this step the system performs diagnosis using the valid method of term (4). Based on the computed diagnoses it tests the dynamic goals.
Using the method of the term (4)
results in the following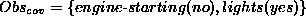 
and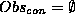 
.
The vocabulary defined by initial-fault-nodes contains
all the initial nodes of Figure 6 that correspond
to fault-modes, plus
all the assumption-symbols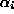 
.
Performing diagnosis results in ``no diagnosis'', which becomes
the verification result.
Critique
The reason for not finding any diagnoses is that there is
no explanation for lights(yes): only incompleteness
assumptions (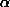
's) and faults are part of
the vocabulary
( initial-fault-nodes), and a fault cannot explain the correct behaviour
of lights(yes) when we use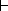 
and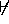 
for
Cover and NotContra respectively. This step determines that
a
possible suitable repair action is adapting the Obs-mapping.
This is so because a different Obs-mapping might require only
incorrect behaviour to be explained (as apposed to all behaviour, including
correct behaviour, as is the case withe the current definition, namely
Obs-mapping=abd-mapping).
Modify
The modify step must now repair the component specified by the critique step. The repair action is determined by first generating a set of variants of the Obs-mapping, and then applying two filters on this generated set of Obs-mapping definitions.
generate: generate variants of
the Obs-mapping component.
We require that any solution of the method using the original Obs-mapping is also a solution for the adapted method with the new Obs-mapping (after all, we want to increase the set of solutions). This relation is expressed in the predicate subset-Es(Old,New). It denotes that the explanations generated by a method with Obs-mapping-component Old are also generated by a method with Obs-mapping-component New, provided all the other components remain the same. In this generation step we generate those Obs-mapping definitions which satisfy subset-Es(abd-mapping,New):
For our problem, the system generates the following set based on its factual knowledge of subset-Es:
The complete definitions of these Obs-mapping components are in [ten Teije & van Harmelen, 1994], but in sloppy notation these definitions are given in table 8.
Figure 8: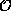 
denotes
the possible observable values, and OBS denotes the
currently given observations
The generated set of Obs-mapping definitions is now:
{cbd-mapping,nor-abnorm-mapping,polarity-mapping}
because subset-Es(abd-mapping,New) holds for these elements.
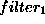: of all the possible candidate repairs, we prefer
the variants that are the ``closest'' to the original Obs-mapping
component:
We define ``closest'' as those Obs-mapping definitions whose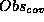 
set
is (1) in any case no superset of the original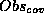 
set (since we do not
want to explain more observable values strongly) and (2) is not a subset of
another possible 
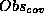set (since we want to
delete as few observable
values as possible).
The predicate
closest-Obs-mapping is therefore defined as follows, whereby
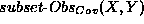denotes that the Obs-mapping
X gives an
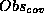set that
is a subset of the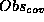 
set computed by the
Obs-mapping Y.
We filter the set based on the following factual knowledge
of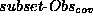 
:
This factual knowledge, just as the knowledge in (5), is stored as given facts in our system. However, given sufficiently powerful theorem-proving techniques, it would be possible for the system to automatically derive these facts from the definitions in table 8. From these definitions, it follows that closest-Obs-mapping holds for the Obs-mapping definitions polarity-mapping and abnormality-mapping. The FilteredSet is therefore:
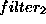: We now filter those variants which result in the
same solutions as the original method in the current case. In this filter the
system executes a part of the diagnosis, namely the Obs-mapping
definition.
The results of the possible Obs-mapping definitions have to be computed
and
compared with the outputs of the original Obs-mapping. Those which
give the
same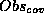 
and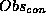 
will be deleted from the set. In contrast
with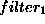 
, this filter is specific for the
current problem on hand,
whereas the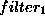 
was independent of the
problem.
Applying the Obs-mapping definitions from (6)
to OBS={light(yes),engine-starting(no)} gives the following
values for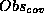 
and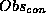 
:
We see that the Obs-mapping with value polarity-mapping gives the same sets as the original Obs-mapping (which had value abd-mapping). The Obs-mapping with value abnormality-mapping gives other sets. This results in a FilteredSet where the only Obs-mapping is abnormality-mapping.
The modify therefore results in the method:
The originally proposed method of term (4) could not handle observed behaviour that was correct behaviour. The above critique-&-modify step tried to recover from this shortcoming by adapting the Obs-mapping component, resulting in the method from term (11). The next step is to verify the adapted method.
Knowledge-verification
The knowledge verification still succeeds, since the Cover-,
NotContra- and Selection-components and the assumptions have
not changed.
(see ``
Knowledge-verification'')
Simulation-verification
Again we perform diagnosis, but now using the modified method of term (11). Performing diagnosis results in the following diagnoses:
Unfortunately, the test whether the dynamic goal max-number-diagnoses(2) is satisfied fails. This means we have to perform another critique step.
Critique
In the verification step the problem of too many solutions was recognized. A repair action for this problem is a modification of the Selection component. If the new Selection component is a stronger filter, then less diagnoses will be left. The system uses the knowledge that constructing the conjunction of the current Selection-component with an additional selection criterion will have this effect.
Modify
The repair action of configuring the new Selection criterion is
executed in
this step. In our case the Vocabulary ( initial-fault-nodes)
contains
faults and incompleteness-assumptions.
We can therefore eomply a selection-criterial that prefers explanations which
are subset-minimal in the incompleteness assumptions
(
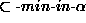). The proposed Selection
criterion then becomes
``
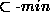and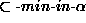 
''.
The adapted method is:
The proposed method from (11) resulted in too many diagnoses. The above critique and modify steps tried to recover from ``too many diagnosis'' and have modified the method. This modified method now has to be verified.
Knowledge-verification
The knowledge verification still satisfies, as before
(
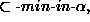also does not violate the
unequal-likelyhood
assumption).
Simulation-verification
Again we perform diagnosis using the modified method of term (9). Performing diagnosis results in the following diagnosis:
Checking this against the dynamic goal shows that we have now also satisfied max-number-diagnoses(2).
We have now (finally!) solved the original diagnostic problem specified in (2). The method of term (9) has explained the observations {engine-starting(no),lights(yes)} under the assumption ``the causes are different in likelyhood'' for the desired goals ``use a standard notion of explanation'' and ``at most two alternative diagnoses are allowed''. The sole computed diagnosis is (14).
During this diagnostic problem solving process the configuration system has had to recover from the initial inability to deal with correct behaviour (by modifing the Obs-mapping component) and it had to recover from ``too many solutions'' caused by too weak a selection filter (by modifying the Selection component).
Propose
