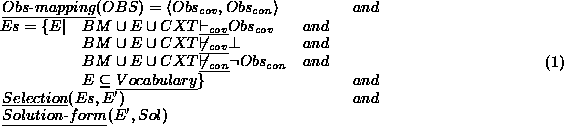
Our approach to automated configuration of problem solvers relies on exploiting the theory about problem solving methods from [ten Teije & van Harmelen, 1994] and [ten Teije & van Harmelen, 1996b]. In that work we have proposed a uniform representation of (the functionality of) problem solving methods. The central idea of this representation is that the functionality of a class of problem solving methods is captured in a single schematic formula. Some of the predicates and terms from that formula are regarded as parameters that must be further instantiated to capture different members of the class of problem solving methods. Thus, given a schematic formula that defines the functionality of a whole class of problem solving methods, different members of that class correspond to different definitions for the parameters occuring in the schematic formula.
It is exactly this uniform representation of an entire class of problem solving methods that will allow us in this paper to view the construction process of problem solving methods as a parametric design task. Since we will illustrate our theory about the configuration of problem solving methods with examples from diagnostic problem solving methods, we will now give our schematic definition of these diagnostic methods.
In general, a diagnostic problem arises if there is a discrepancy between the observed behaviour of a system (e.g. an artifact) and how the system should behave, in other words, the expected behaviour does not correspond with reality. The diagnostic task is to find out the cause of this discrepancy. A diagnostic method computes the solutions for a diagnostic problem by using a model of the expected behaviour (the behaviour model, BM), the actually observed behaviour OBS, and contextual information CXT. The computed solutions of a diagnostic problem represent an explanation for the observed behaviour.
Our uniform representation of diagnostic problem solvers is based on the following general account of their functionality: An explanation distinguishes two types of observations: it covers some observations, and it does not contradict other observations. The explanation is restricted to a vocabulary of special candidates that could be causes of a behaviour discrepancy (e.g. components). Usually we are not interested in all possible explanations, but only the most reasonable explanations. We also want to represent an explanation as a solution that a user can interpret. (For example, in medical domains, users are usually interested in the disease, and not in all the current states of the parts of the patient's body).
Together, these six aspects written in italics make up the particular notion of diagnosis that is realised in a given method. We can capure these general characteristics of a diagnostic method in the following formal definition:
When given as input the behaviour model BM, a context CXT and a set of observations OBS, a diagnostic method computes a set of solutions Sol such that:
Each of the six underlined terms is one of the parameters in our
representation of diagnostic methods. Varying one or more parameters amounts
to describing a different diagnostic methods. The Obs-mapping
determines
which observations must be explained (or: covered)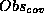 
, and which
need only not be contradicted (
).
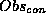E is an explanation for the
observed behavoiur by covering some observations (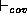
), and not
contradicting others (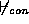
). We write 
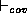and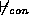 
as different symbols to emphasise that one is not
necessarily the negation of the other, and that neither is necessarily the
same as the classical entailment 
.
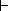E is expressed in a particular
Vocabulary. We are interested in the most reasonable explanations,
determined by a Selection criterion. The Solution-form
determines the
representation of the final result of the method. The dependencies between
all these components of a diagnostic method is shown in figure
1
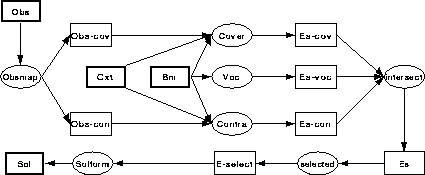
Figure 1: Components of diagnostic methods and their
relations.
Ovals are components, boxes are their inputs/outputs, thick boxes are
inputs/outputs of the entire method
In [ten Teije & van Harmelen, 1994], we show that we can formulate properties of this general schematic formula, as well as properties of instances of the schema. Such properties will be exploited in the configuration of methods. In [ten Teije & van Harmelen, 1996b] we have argued that this representation can in principle be applied to other families of methods than diagnostic methods, such as methods for monitoring, design, classification etc. As a result, we will claim that also our approach to the configurtion of methods is general, and could be applied to such other families of problem solving methods.
