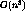 , where n is the number of instances in
the database.
When the number of instances increases, its time complexity becomes a
significant problem.
, where n is the number of instances in
the database.
When the number of instances increases, its time complexity becomes a
significant problem.
Yuiko Ohta, Seishi Okamoto - Nobuhiro Yugami
Fujitsu Laboratories Ltd.
2-1-1, Momochihama Sawara-ku, Fukuoka 814, Japan
{ yuiko, seishi, yugami }@flab.fujitsu.co.jp
Clustering systems can discover intentional structures in data and extract new knowledge from a database. Many incremental and non-incremental clustering algorithms have been proposed, but they have some problems. Incremental algorithms work very efficiently, but their performance is strongly affected by the input order of instances. On the other hand, non-incremental algorithms are independent of the input order of instances but often take a long time to build clusters for a large database. Moreover, most of incremental and non-incremental algorithms build concept hierarchies with single inheritance. Many real world problems require different points of view to be solved. Concept hierarchies with multiple inheritances are useful for such problems. We propose a non-incremental and efficient algorithm which builds concept hierarchies with multiple inheritances.
Clustering systems can discover intentional structures in data. It groups instances which have similar features and builds a concept hierarchy. As a result, it often extracts new knowledge from a database. Because of the ability to find the intentional descriptions, it is one of the very important techniques in managing databases.
There exist many incremental and non-incremental clustering algorithms (e.g., COBWEB [Fisher1987] [Fisher1995], LABYRINTH [Thompson & Langley1991]). Incremental algorithms work very efficiently, but the generated cluster hierarchy and its performance strongly depend on the input order of instances.
There are also many non-incremental algorithms (e.g., CLUSTER/S
[Stepp & Michalski1986]).
These aren't related to that problem, but they take a long time to create
clusters.
For example, Ward's method initially makes each cluster which is composed of
each instance.
It iteratively merges two clusters which are the most correlated.
It must calculate a correlation for every two clusters and select the best
pair in each step.
Then Ward's method takes 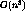 , where n is the number of instances in
the database.
When the number of instances increases, its time complexity becomes a
significant problem.
, where n is the number of instances in
the database.
When the number of instances increases, its time complexity becomes a
significant problem.
In addition to the above problem, both incremental and non-incremental algorithms have another characteristic. Most of them build a concept hierarchy on which each instance belongs to only one cluster. Real world problems often require several different points of view. A concept hierarchy with multiple inheritances is more suitable in those cases.
We propose a new algorithm which is non-increment, and efficient. Moreover, our method builds hierarchical concepts with multiple inheritances.
In this section, we give an overview of our algorithm. We assume every attribute is nominal. Our algorithm intends to assign each instance to more than one suitable group.
Table 1 shows the outline of our algorithm.
Firstly, our algorithm creates an initial concept hierarchy composed of a
root and leaf clusters but no intermediate cluster ( Figure 1 ).
Each leaf cluster corresponds with an attribute value and consists of all
instances with 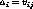 .
Then it iteratively improves the hierarchy by generating a new cluster from
two ones and linking the new one to others.
.
Then it iteratively improves the hierarchy by generating a new cluster from
two ones and linking the new one to others.
Table 1: Clustering algorithm
In the following subsections, we describe how to select two clusters at the Select step and how to generate a new cluster at the Generate step.
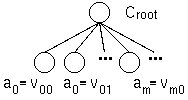
Figure 1: An initial hierarchy
At the Select step in Table 1, our algorithm finds a pair of strongly related clusters to combine them at the Generate step. In our algorithm, an instance can belong to multiple clusters. We measure the similarity of two clusters with the number of instances that appear simultaneously in two ones.
Assuming two clusters are independent, the expectation of instances common to them can be calculated. If the actual number of the common instances is far from its expected, we can conclude there exists some relation between two clusters.
The expectation of the instances common to two independent clusters 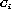 and
and 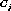 and its standard deviation are,
and its standard deviation are,
where n is the number of instances in the database.
Two clusters has some relationship, when the actual number 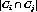 satisfies the following.
satisfies the following.
k is a parameter.
Our algorithm selects the pair, 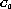 and
and 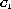 , maximizes Eq.(4)
among all pairs which satisfy Eq.(3).
, maximizes Eq.(4)
among all pairs which satisfy Eq.(3).
Of course, when one cluster of the pair is an antecedent of the other, the pair is excluded from consideration.
We adopt the above function to measure the relationship between two clusters, because of its ease of calculation. However, our algorithm can use other criteria. Several measures of relationship have been proposed. For example the category utility in COBWEB and correlation will become alternative methods to measure the relationship between two clusters.
At the Generate step, we use two operators to generate a new cluster,
a generalization operator and a specialization operator (Figure
2).
The generalization operator generates a new cluster that represents a
disjunctive concept of the original clusters, 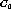 and
and 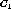 .
The generated cluster,
.
The generated cluster, 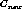 consists of
consists of 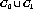 .
The specialization operator generates a new one which represents a
conjunctive concept of
.
The specialization operator generates a new one which represents a
conjunctive concept of 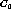 and
and 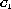 , and the new cluster consists of
, and the new cluster consists of
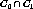 .
.
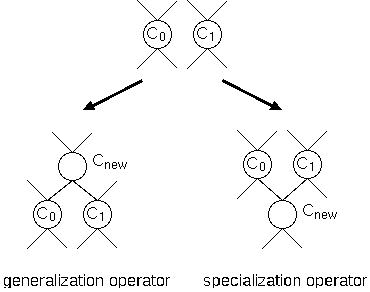
Figure 2: Generating operators
There exist some strategies to control these operators. The most simple strategy is adopting only a generalization or specialization operator. The second strategy has two phases. The first phase uses only one operator to make new clusters, and in the second phase the other is adopted. The last strategy is to choose a better operator at each iteration and to operate the better one. The last one needs a reasonable criterion for choosing which is a better operator.
In our algorithm, the iteration of Select and Generate
terminates when there is no pair which satisfies Eq.(3) in the
hierarchy, or the size of the concept hierarchy becomes L, given as a
parameter.
We generally do not need a very complicated hierarchy.
Therefore, the limitation L can be set at a relatively small number
compared with n.
The time complexity of our algorithm is 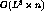 ,
hence our method creates the concept hierarchy within reasonable time for a
large number of instances.
,
hence our method creates the concept hierarchy within reasonable time for a
large number of instances.
Table 2: Datasets for experiments
In this section, we show the results of experiments. We applied this algorithm to 4 datasets in UCI repository (Table 2). The third column ( domain ) is the total number of domain sizes for all attributes. The sum of the third and the fourth column is the number of initial leaf clusters.
We evaluated the performance of our algorithm by predicting attribute values with generated concept hierarchies. For each dataset, we built clusters with the specialization operator from the training set and set 1.8 as k in Eq.(3). We predicted the value of each attribute for each instance in the test set. The accuracy of predictions is given in Table 3 which was averaged through twenty-fold cross validation.
We used only leaf clusters to predict values in these experiments.
We calculated the following probability for each cluster C to predict the
value of the missing attribute  of a test instance
of a test instance
 .
.
where 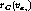 is the probability of instances with
is the probability of instances with 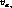 in
the cluster C.
The system chose a cluster which maximized the probability Eq.(5),
and predicted
in
the cluster C.
The system chose a cluster which maximized the probability Eq.(5),
and predicted  as the most frequent value in the chosen cluster.
as the most frequent value in the chosen cluster.
Table 3: Averaged accuracy of predictions
In Table 3, the second column is the accuracy for class attribute, the third is the accuracy for all attributes, and the last is the accuracy for all attributes [Fisher1995].
We think the accuracy of predictions by our algorithm was good enough for the first trial, but it had large standard deviations. One of the reasons for the large deviations is that we used only leaf clusters to predict values. If we make use of more information, such as the number of instances in each cluster, and the structure of a hierarchy, the accuracy will be improved and will become more stable. In order to show that our algorithm can support concepts with multiple inheritances, we have to use the problem which needs multiple viewpoints to be settled. But there is no such standard dataset, then we show only the results of predictions of missing attributes' values.
We have presented a new algorithm for clustering. It is non-incremental and builds a concept hierarchy efficiently. So it is not affected by the input order of instances and can be applied to a large-scale database. Moreover, it creates a hierarchy with multiple inheritances. Hence, we expect it will be useful where different perspectives are needed to solve a problem.
There are still several ways to improve this algorithm. The first point is which criterion is appropriate for selecting a pair of clusters to generate a new cluster. As mentioned, category utility and other proposed measures can replace our criterion with small changes. Most of them originally assume an instance belongs to only one cluster. For our algorithm, they should be modified such that an instance is considered to belong to multiple clusters.
The next point is how to use two generate operators at the same time. The most simple way is to apply both operators every time. But this is a waste of computing time, because the disjunctive and conjunctive clusters aren't always both useful. One way is to choose the operator which can make a larger change to the concept hierarchy, that is which generates a more diffrent cluster from other clusters.
Furthermore, we need to consider better methods to predict the missing value. Each cluster made by this algorithm is described with the and/or of attribute values and links more specialized or generalized concepts. If we use these information effectively, we will be able to predict attribute values more precisely.
Finally, we will consider which domain is appropriate for our algorithm. This algorithm aims at performing well with problems which need multiple viewpoints to be solved. We should apply this algorithm to such problems, and confirm its effectiveness.