A Resolution method specifies how a task without further subtasks
gets accomplished. Resolution methods consult, generate or modify the
contents of models in order to carry out a task. This makes them
meta-theories of the object-theories representing those models. They
exploit some relationship among the contents of their inputs to
generate the contents of their outputs. This relation is formally
represented by an atomic formula of the form 
, where name is the name of the resolution
method and 
are terms describing the syntactical
structure required for its arguments. The actual relationship is
defined by a set of axioms of the form 
, where 
can be
any formula constructed from atomic formulae of the form
and other predicates. In order to capture the
executable aspect of resolution methods, we formalize them as
Quantified Dynamic Logic (QDL) meta-theories. The QDL test operator
? allows us to turn the atomic formula associated to a
resolution method into a test program 
. The execution state of a method is represented by
state variables of the form 
, which contain the
list of values that have been used or computed so far for
each argument. The program 
, which adds an element to the
front of a list, is used to store used or computed values for
arguments in their respective state variables, and therefore to modify
the execution state of the method. A QDL program 
is defined in order to specify the
behavior of a resolution method, i.e how it modifies its state of
execution in each circumstance.
sorts sort tree
constants (constantsymbol +: sortsymbol) *
functions (functionsymbol +: sortsymbsortsymbol) *
predicates (predicatesymbol +: sortsymbol *) *
variables (variablesymbol +: sortsymbol) *
metavariables (varsymbol +: metatype) *
axioms
*
program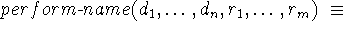
a QDL program made from
conditions and programs on
The following examples show the formal descriptions of some resolution methods.
\
