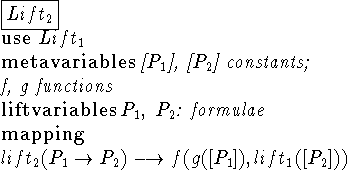are a particular class of resolution methods which translate between the vocabularies and representation formalisms of different models. They allow resolution methods to use the knowledge contents of different models by establishing mappings between the representation formalisms used by models (formula-schemas) and resolution method arguments (term-schemas). The possibility of establishing these mappings enhances the reusability of models and methods across domains, as we will see in section 3. Meta-variables and lift-variables are used respectively to describe the syntactical structure of formula-schemas and term-schemas. Mappings provide the translation rules between formula-schemas and term-schemas.
use*
sorts sort tree
metavariables (metavar +: metatype) *
liftvariables (varsymbol +: metatype) *
mappings (lift(expression)termschema) *
The operator use allows including a lift definition (i.e. its language and mappings) within a theory or another lift definition.
A partial order relation 
, which formalizes the notion of
instance, can be defined on term and formula schemas (s
denotes a substitution).
1. Letbe two formulaschemas,
if
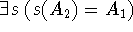
2. Letbe two termschemas
if
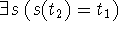
A mapping 
is a total, bijective, bothsides order preserving
function
Total: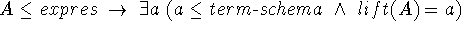
Bijective:
1.
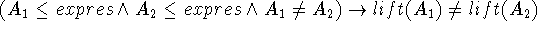
2.
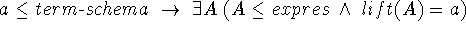
Bothsides order preserving:
1.
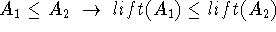
2.
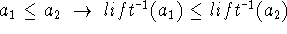
The following examples show the formal descriptions of some lift
definitions. Note that 
uses 
as part of its
definition.
\
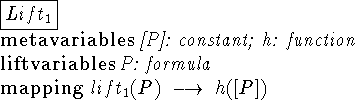