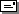 Rob Kremer
Rob Kremer

Practical Software Engineering
Metrics
( Note:
These notes are based on material in Chapter 20 of the book
Software Engineering: A Practitioner's Approach,
Third Edition, by Roger S. Pressman)
A quality metric is a number that represents one facet or
aspect of software quality.
For example, in the last lecture, availability was
defined to be the ratio of the total time that the software was up, to
the sum of the time that it was up and the sum that it was down.
This is a metric that represents one aspect of the software quality
factor, reliability.
Application to Assessment of a Quality Factor
Frequently, a software quality factor is measured (or estimated) by
determining the values of several related metrics and forming a
weighted sum:
Fq = c1 m1 + c2 m2 + ... + cn mn
where
-
Fq represents a software quality factor we are
interested in but that is difficult to measure directly;
-
m1, m2, up to mn are metrics whose
values can be determined relatively easily, and that are
related to the software quality factor; and
-
c1, c2, up to cn are regression
coefficients - real numbers that are fixed from system to system (or
project to project) and determine the way and extent that the value of
each metric affects the software quality factor.
Values for regression coefficients are generally set (or, perhaps,
estimated) by examining data from past projects and estimating the
relative importance of each metric for the quality factor to be
determined. The greater the amount of this past data that is
available, the more accurate the regression coefficients are likely to
be!
Two Types of Quality Metrics
-
A product metric is a number derived (or extracted) directly
from a document or from program code.
-
A process metric is a number extracted from the performance
of a software task. As defined above, availability is a process metric
that is related to software reliability.
Uses of Metrics for SQA
Quality metrics are useful
- as a quality assurance threshold: Minimal (or maximal) acceptable
values for metrics can be stated in requirements specifications, in
order to set comprehensible and testable requirements related to quality
factors (besides functional and performance requirements).
- as a filtering mechanism. For example, it's frequently true that
sufficient resources aren't available for a thorough inspection of all
the code associated with a project. It's known that code which is more
complex will generally be
more difficult to maintain and test than less complex code. A
complexity metric can be used to identify the most highly complex code
that is part of the current software project - and care can then be
taken to inspect and test this code more thoroughly than would be
possible if all the code received the same attention.
- to evaluate development methods. It is (therefore) desirable to
maintain a database of statistics about past projects.
- to help control complexity, especially during maintenance. The
complexity of code tends to increase as it is maintained and
changed. It may be less expensive (in the long run) to redesign and
recode a complex module, than it would be to continue to try to
"patch" it.
- to provide staff with feedback> on the quality of their work. Once
again, complexity metrics are useful for an example: If several
designs are being considered then it is generally worthwhile to choose
the one that is the least complex - provided that it is not
disqualified for other reasons. Thus, metrics can be useful for comparing
proposed solutions for problems, and choosing between or among them.
Complexity
Complexity is a measure of the resources which must be expanded in
developing, maintaining, or using a software product.
A large share of the resources are used to find errors, debug, and retest;
thus, an associated measure of complexity is the number of software errors.
Items to consider under resources are:
- time and memory space;
- man-hours to supervise, comprehend, design, code, test, maintain and
change software; number of interfaces;
- scope of support software, e.g. assemblers, interpreters, compilers,
operating systems, maintenance program editors, debuggers, and other utilities;
- the amount of reused code modules;
- travel expenses;
- secretarial and technical publications support;
- overheads relating to support of personnel and system
hardware.
Consideration of storage, complexity, and processing time may or
may not be considered in the conceptualization stage. For example, storage of
a large database might be considered, whereas if one already existed, it could
be left until system-specification.
Measures of complexity are useful to:
- Rank competitive designs and give a "distance" between rankings.
- Rank difficulty of various modules in order to assign personnel.
- Judge whether subdivision of a module is necessary.
- Measure progress and quality during development.
Program complexity can be logical, psychological or structural.
can make proofs of correctness difficult, long, or impossible, e.g.
the increase in the number of distinct program paths.
makes it difficult for people to understand software. This is
usually known as comprehensibility.
involves the number of modules in the program.
Logical complexity has been measure by a graph-theoretic measure.
McCabe calculates the paths through a program. Each node corresponds to
a block of code, each arc to a branch. He then calculatesthe cyclomatic number
(maximum number of linearly independent circuits), and controlling the size by
limiting this.
He found that he could recognize an individual's programming style by the
patterns in the graphs. He also looked at structure, and found that only 4
patterns of 'non-structure' occur in graphs, which are:
- branching out of a loop
- branching into a loop
- branching into a decision
- branching out of a decision
In summary, this is a helpful tool in
preparing test data, and provides useful information about program complexity.
However, it ignores choice of data structures, algorithms, mnemonic variable
names, comments, and issues such a portability, flexibility, efficiency.
Structural complexity may be absolute or relative. Absolute structural
complexity measures the number of modules, relative structural complexity is
the ratio of module linkages to modules. The goal is to minimize the
connections between modules over which errors could propogate.
Cohesiveness refers to the relationships among pieces of a module.
Binding is a measure of cohesiveness; goal is high. It could be
- coincidental,
- logical,
- temporal,
- communicative sequential or
- functional.
This includes such issues as:
- high and low-level comments
- mnemonic variable names
- complexity of control flow
- general program type
Sheppard did experiments with professional
programmers, types of program (engineering, statistical, nonnumeric), levels of
structure, and levels of mnemonic variable names. He found that the least
structured program was most difficult to reconstruct (after studying for 25
minutes) and the partially structured one was easiest. No differences were
found for mnemonic variable names, nor order of presentation of programs.
Shneiderman suggest as 90-10 rule, i.e. a competent programmer should be able
to reconstruct functionally 90% of a program after 10 minutes study (or module
if large program). A more casual approach would be 80-20 rule, a more rigorous
approach would be 95-5 rule. This is based on memorization/reconstruction
experiments.
Complexity theory does not yet allow us to measure the separate aspects, e.g.
problem, algorithm, design, language, functions, modules and combine them to
measure and compare overall complexity. Most complexity measures concentrate
on the program. Instruction counts are used to predict man-hours and
development costs. A high level language may have between 4:1 and 10:1 ratio
to machine language.
Statistical approach, used by Halstead, looked at total number of operators and
operands, and related this to man-hours. This measure was rooted in
information theory -- Zipf's laws of natural languages, Shannon's information
theory.
Consideration of the length and difficulty of individual program statements
does not account for the interrelationships among instructions, i.e. structural
intricacy. Most work on structural complexity relates to graph topological
measures. Graph theory is not able to represent storage, or operands. It
concentrates on transfer of control.
Similar to set theory: collection X, mapping M
e.g. X-set elements, M-set mapping rules
- Positions of pieces on a chess board
- Rules for moving and capturing pieces
- A group of relatives
- Units of electrical appratus
- Wires connecting the units
- Instructions in a computer program
- Rules of syntax a sequence which govern the processing of the
instructions
Each element belonging to X is represented by a point
called a vertex or node. Mapping rules define connections between the
vertices. If there is an order in the connection, or arc then it is a directed
graph or digraph. If there is no order the connecting line is an edge.
A directed graph and a "regular" graph
- Two arcs are adjacent if they are distinct and have a vertex
in common.
- Two vertices are adjacent if they are distinct and there
exists an arc between them.
- A path is a sequence of arcs of a graph such that the terminal
vertex of each arc conicides with the initial vertex of the succeeding arc.
- A path is simple if it does not use the same arc twice, and
composite otherwise.
e.g. 1, 3, 7 or a, b, x, d is a simple path 1, 3, 4, 4,
7 or a, b, x, x, d is composite
- A path is elementary if it does not meet the same vertex more than
once.
e.g. simple: (1, 3, 7), (1, 3, 4, 7), (1, 3, 6, 5, 7) elementary: (1,
3, 7) only
- A circuit is a finite path where the initial and terminal nodes
coincide.
- An elementary circuit is a circuit in which no vertex is traversed
more than once.
- A simple circuit is a circuit in which no arc is used more than
once.
- The length of a path is the number of arcs in the sequence.
- The length of a circuit is the length of its path.
- A digraph is complete if every distinct node pair is connected in
at least one direction, e.g. node e is not connected, so graph is not complete.
- A digraph is strongly connected if there is a path joining every
pair of vertices in the digraph, e.g. not strongly connected as can not go d to
c.
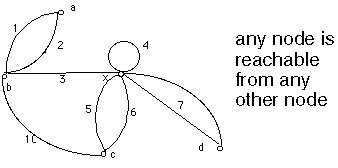
In linear algebra, a set of vectors x1, x2, ..., xn is linearly
dependent if there exists a set of numbers not all zero s.t. a1x1 +
a2x2 + ... + anxn = 0. If no such set of numbers exists then the set
of vectors are linearly independent.
Any system of n linearly independent vectors e1, e2, ..., en forms a
basis in n-dimensional vector space.
In graph theory, if the concept of a vector is associated with each circuit or
cycle, then there are analogous concepts of independent cycles and a cycle
basis.
The cyclomatic number vG of graph G is equal to the maximum number of
linearly independent cycles. The cyclomatic number vG of a strongly
connected digraph is equal to the maximum number of linearly independent
circuits. vG = m - n + p
where there are m arcs
n vertices
and p separate components
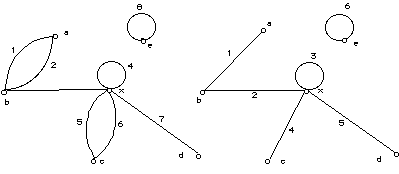
e.g. m=9, n=5, p=1, vG=5
There are various other methods for calculating the cyclomatic number of a
graph.
A program graph is obtained from shrinking each process and decision symbol in
a flowchart to a point (vertex) and lines joining them (arcs). Direction in a
program is important, hence a directed graph (digraph) is obtained.
e.g. digraph of program flowchart given:
nodes a and k correspond to start and stop nodes
node c corresponds to GET A
node i corresponds to L = L + 1
The cycle (loop) is composed of arcs 4, 5, 6, 7, 8
IF THEN ELSE appears as 5, 6 and 9, 10.
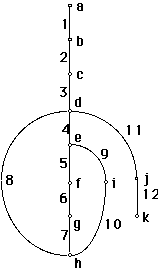
The cyclomatic number of the digraph gives a complexity
metric. Comparisons show that a high cyclomatic complexity is associated
with error-prone programs.
A graph is constructed with a single start node and a single stop node. If
there is an unreachable node, that represents unreachable code or coding error
which must be corrected.
In general the graph is not strongly connected, so form a loop round the entire
program (phantom arc).
e.g. vG= 13 - 11 + 1 = 3
number of arcs m = 13
number of nodes (vertices) n = 11
separate parts p = 1
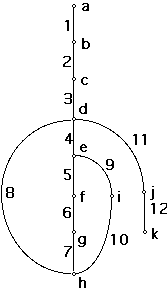
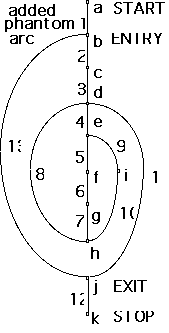
Results
McCabe says that vG is a good measure of complexity and all modules
should have vG<10. This replaces the general rule of thumb that a
module should be one page of code (50 to 60 lines). He has shown that programs
with a large vG are error-prone.
Much theory exists in this area, but as yet has not been applied on a wide
scale.
Adapted from notes by Dr. Wayne Eberly and Dr. Mildred Shaw
 Practical Software Engineering, Department of Computer Science
Practical Software Engineering, Department of Computer Science
 Rob Kremer
Rob Kremer
 Rob Kremer
Rob Kremer


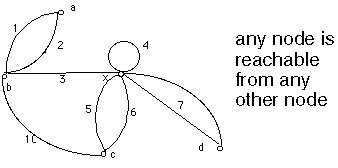




 Practical Software Engineering, Department of Computer Science
Practical Software Engineering, Department of Computer Science
 Rob Kremer
Rob Kremer