The topological ontology defines a relation to express the fact that mereological individuals are connected. We want to use this relation to define connections in the component view of a physical system, where being connected means being able to exchange energy. Because we have this application in mind, the topology must be capable of stating three things:
A well known way of expressing topological information is described by B. L. Clarke [Clarke, 1981]. He introduces a relation Cx,y to express that individuals x and y are connected. Unfortunately, given this relation, it is only possible to express that there are two connections between two individuals when connections are regarded as a special kind of individuals themselves. We find this point of view debatable, because a physical connection can be a point of contact (mechanical, electrical), an area crossing a volume flow (hydraulical, pneumatical) or even something abstract as a field (electro-magnetic). We have therefore introduced connections as a relation between individuals and reified the relation into the connection concept to allow for multiple connections that can be typed. This has led to the relation connects(c,x,y) which means that individuals x and y are connected by connection c (see Figure 4).
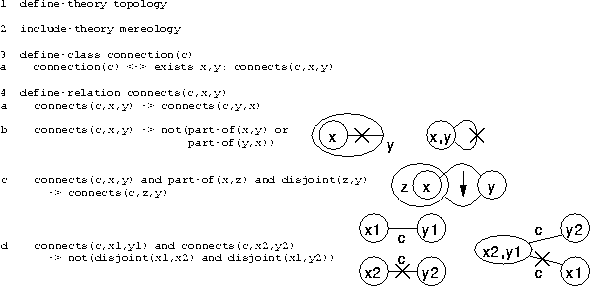
Figure 4:
Excerpt from the topological ontology. This ontology provides the
means to express that individuals are connected. Axioms ensure that
only sound connections can be made. These axioms take into account
the possible part-of decomposition an individual can have.
The projection performed in this ontology is of the type include and extend. Inclusion is done in line 2 and the extension takes shape by definition of new concepts and relations that use mereology in their axioms. This yields an ontology that has the same level of abstraction as the included mereology. There are three axioms concerning connections. The symmetry of the connection relation is expressed by axiom 4a. Axiom 4b prohibits that a part is connected to itself or its whole (part-of(x,y) holds iff x is a proper part of y or they are equal). The third axiom (4c) ensures that when a part whose whole is disjoint with an individual connected to the part, the whole is also connected to that individual. The fourth axiom (4d) prohibits a connection to connect two entirely separated pair of individuals. This also excludes connections that fork.