One particular viewpoint on a physical system is that it is a system in the sense of general systems theory. That is, it constitutes an entity that (i) can be seen as separate from the rest of the world --so it has a boundary and an outer world, the environment-- and that (ii) has internal structure in terms of constitutive elements and subsystems maintaining certain mutual relationships.
For physical systems this implies that we focus on the structural aspects, and abstract from what kind of dynamic processes occur in the system and from how it is described in terms of mathematical constraint equations. Within such a purely structural view, we can express the following knowledge about the system:
An example of a structural-topological diagram for a physical system, i.c. an air pump, is shown in Figure 2. This structural view on physical systems is based upon what we call a component ontology.
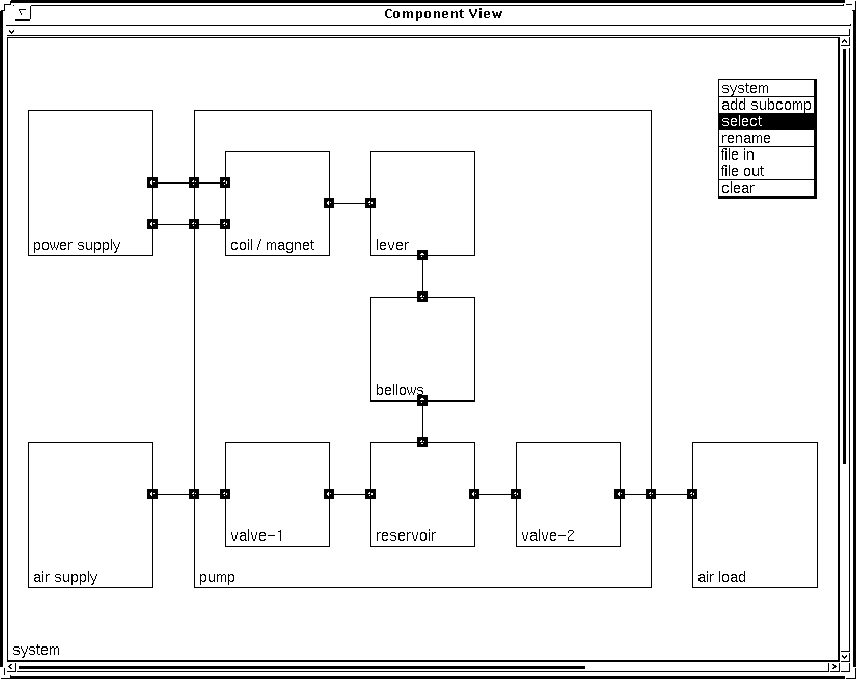
Figure 2:
The component view on a physical system, showing a two-level
part-of decomposition and the system topology for an air pump.
Sub-components are drawn inside the area defined by their
super-component. The small solid blocks are the interfaces through
which components are connected.
Our component ontology is constructed from mereology, topology and systems theory. In a separate ontology of mereology a part-of relation is defined that formally specifies the intuitive engineering notion of system or device decomposition. This mereological ontology is then imported into a second separate ontology which introduces topological connections that connect mereological individuals. This topological ontology provides a formal specification of what the intuitive notion of a network layout actually means and what its properties are. The ontology of systems theory includes the topological ontology and defines concepts like (open or closed) systems, system boundary etc. on top of it.