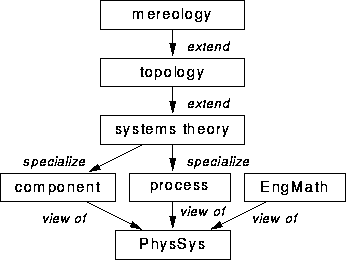
Figure 1: Inclusion lattice of the PHYSSYS ontology.
PHYSSYS is a formal ontology based upon system dynamics theory as practiced in engineering modelling, simulation and design. It forms the basis for the OLMECO library, a model component library for physical systems like heating systems, automotive systems and machine tools. The ontology expresses different conceptual viewpoints on a physical system. To demonstrate what these viewpoints are, we carry out the small exercise of determining the knowledge that is required to understand the formula F=ma. Anybody who paid attention during physics class at highschool knows that this formula is Newton's law that describes the acceleration of an object under the influence of a force. Unfortunately, for a computer this is not obvious at all...
When a user types in the formula on the console, it is just a string of characters. Assuming the computer knows about mathematics, this string will be parsed and identified as a mathematical formula, a relation between variables. The mathematical knowledge must include the facts that variable stands for a certain value that may or may not change in time (or another free variable) and that possibly has a certain dimension. Knowing all this, F=ma just means that the value of one variable is equal to the product of the value of two other variables, at any time. The system still knows nothing about its meaning in terms of physics.
In order to make the computer understand the physical implication of the formula it must know about physical processes, energy and physical domains. It must know that a formula can be a mathematical description of a physical process like the inertial effect of a mass. At this point it also becomes clear that a mathematical variable represents a certain physical quantity. In the F=ma example, F is a force quantity, m stands for a mass and a for an acceleration. Without this knowledge F=ma could also have meant that the voltage F is equal to a resistance m multiplied by the electrical current a. With this interpretation, the equation would have been another famous physical law called Ohm's law (usually written down as V=IR) that describes the process of electrical resistance.
The final step is to introduce the relation between the physical processes and the real world physical system. For this, knowledge of how people look upon physical systems is required. In engineering it is customary to think of the system as a configuration of components which on their turn can be decomposed into smaller components. Connections between components are the means for interaction. In these terms, the mass could be a heavy object hoisted by a crane. The load and cable would be two components connected to each other by a mechanical connection. Each component is the carrier of physical processes. The load component is the carrier of the inertial effect and its interaction with the cable component implies an energy flow between the physical processes modelling the two components.
Accordingly, it is clear that three conceptual viewpoints on physical systems can be distinguished: (i) system layout, (ii) physical processes underlying behaviour and (iii) descriptive mathematical relations. The PHYSSYS ontology consists of three engineering ontologies formalizing these viewpoints. The interdependencies between these ontologies are formalized as ontology projections. Furthermore, the viewpoints themselves are constructed from smaller abstract ontologies. The whole set of ontologies used contains ontologies of varying genericity and abstractness. Identifying these separate ontologies not only makes it easier to understand the domain because classes and ontological commitments are added incrementally, it also increases the ability to share and reuse parts of PHYSSYS.
Figure 1 gives an overview of the structure of the PHYSSYS ontology [Borst et al., 1994, Borst et al., 1995]. Boxes represent separate ontologies whereas labeled arrows indicate ontology inclusion. The labels next to the arrows show the kind of inclusion. As can be seen in the figure, the PHYSSYS ontology consists of three primary ontologies which are formalizations of the three views on the physical domain. In the next sections these ontologies will be explained as well as the mereological, topological and system theory ontologies that are used in both the component and process ontologies. Special attention will be given to the ontology projections, which are the formalizations of the interdependencies between included ontologies.

Figure 1: Inclusion lattice of the PHYSSYS ontology.